布料包裝設備中翻折機構的結構設計與運動分析

李 彬，孫志宏，b

(東華大學 a.機械工程學院,b.紡織裝備教育部工程研究中心, 上海)

公理化設計(axiomactic design, AD)理論[1]通過運用科學嚴謹的設計公理與方法,為結構方案的設計與評估指明依據。韓軍等[2]采用公理化設計理論結合層級映射關系獲得可行的設計參數,實現了對設施蔬菜種植微小型旋耕機造型的創新設計。唐峰等[3]在設計用于鞭炮產品的機構中,以公理化設計理論為出發點,建立功能模塊并分析其中的映射關系,結合成本控制的方法規范了產品設計流程,節省了成本。房德磊等[4]利用公理化設計原理,從概念設計出發分析設計過程中的耦合情況,并對結構模型進行仿真分析,設計出一款適用石油水平井特殊條件下的全液壓驅動管道機器人。但目前在紡織機械領域的產品設計中極少采用公理化設計方法進行機構設計或優化分析,故本文以公理化設計方法為指導,開展布料包裝設備中翻折機構設計與分析。

1 公理化設計概述

作為新的概念性設計理論,AD理論提出了設計域的概念,通過劃分用戶域、功能域、結構域和工藝域等4個設計域來剖析整個設計流程[5]。4個設計域對應的元素分別為用戶需求(customer attributes,CAs)、功能要求(functional requirements,FRs)、設計參數(design parameters,DPs)和過程變量(process variables,PVs)[6]。因此,產品設計為公理化設計4個設計域的映射過程,如圖1所示。按實際設計需要生成設計層級樹,以功能特性和結構特性設計的復雜產品方案進行案例分解,得到不同設計層次的設計需求[7]。設計層級樹可清晰地描述出功能設計域和結構設計域的設計目的,如圖2所示。

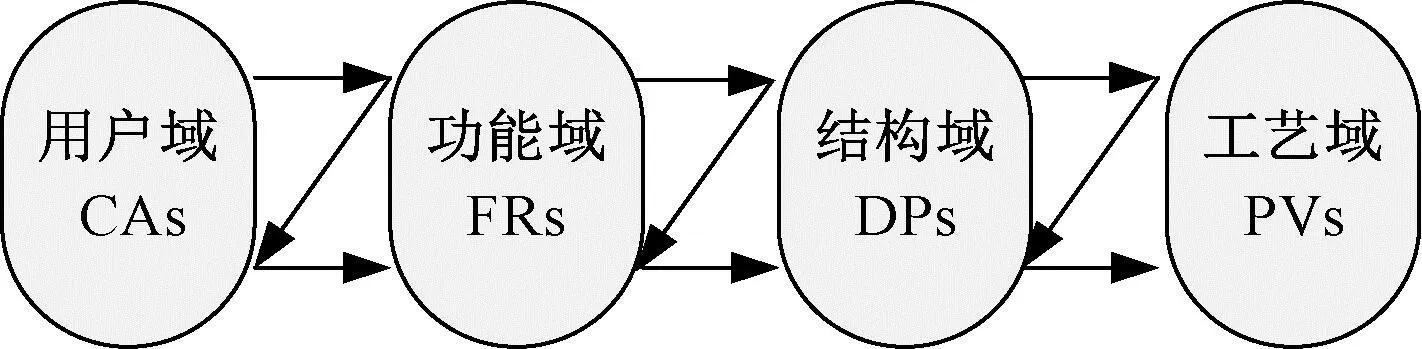
圖1 公理化設計域映射過程Fig.1 Axiomatic design domain mapping process

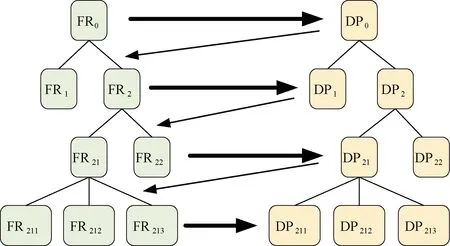
圖2 功能特性與結構特性層級樹Fig.2 Hierarchical tree of functional and structural properties

AD理論的重點內容包含了獨立性公理和信息公理,可用來指導復雜產品的方案設計[8]。獨立性公理是指在FRs滿足相互獨立的前提下,DPs與其他的 FRs 不存在耦合牽連關系[9]。信息公理是以獨立性公理為前提,在不同設計方案中所含信息量最少的設計是最優設計[10]。

2 翻折機構概念化設計分析

2.1 翻折機構多級域設計分析

翻折機構是紡織產業鏈中布料經染整工序處理后的一種包裝設備,用于實現布料的運輸、貯藏以及進一步加工。用戶(企業)提供了包裝布料的幅寬范圍和最重的質量,并對布料包裝提出要求。翻折機構配合碼布機(為計量布料總長,利用碼布機上擺桿來回1 m擺動將布料層疊碼放)進行布料的包裝(布料參數：幅寬為1.4～2.2 m,布卷質量為小于30 kg),既要保證操作的安全與穩定,同時需依據現有的生產方式進行設計,由此列出企業需求指標如表1所示。

表1 用戶需求明細Table 1 Breakdown of user requirements

本文將用戶需求定義為“使用布料包裝翻折機構”,將第一層級功能需求“翻轉折疊”設定為FR,用“翻折機構”實現前述需求,設定為DP。基于設計目標,翻折機構具有提供翻折動力、避免工作干涉、滿足舒適性和實現翻折4項基本功能。為實現該4項基本功能,第二層級系統設計對應功能需求的設計元素包括運動輸出單元、對稱翻折結構、舒適的工作臺高度以及翻折元件。其中完成翻折功能要求又可分為滿足不同的布料幅寬與翻折過程平穩,故設計域第三層對應功能域第三層為可伸縮元件與運動特性的要求。功能域與設計域的各個層級對應元素分析完成如表2所示,兩者的映射關系如圖3所示。

表2 功能域與結構域元素Table 2 Elements of functional and structural domains

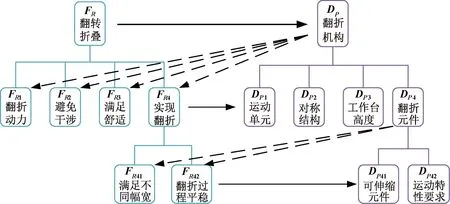
圖3 功能域與結構域層級映射關系Fig.3 Functional domain and structural domain hierarchy mapping relationship

2.2 機構設計耦合分析

用產品設計方程表示公理化設計域間層次結構中某一層級的功能需求與該層設計域中的設計參數之間的關系[11],如公式(1)所示：

或{FR}m×1=Am×n{DP}n×1

(1)

式中：{FR}m×1為功能需求向量;{DP}n×1為設計參數向量;Am×n為產品設計矩陣。

根據設計矩陣的不同結構形式可分為3種類型,其與獨立性公理的關系如表3所示。

表3 設計矩陣與獨立性公理關系Table 3 Design matrix and independence axiom relationship

本研究的翻折機構的功能域與結構域：第一層為單元素的映射過程(見圖3),屬于非耦合獨立設計;第二層功能域到結構域映射關系如式(2) 所示;第三層映射關系如式(3) 所示,設計矩陣非零元素都在對角線上,即第二層和第三層的功能域與設計域之間屬于非耦合設計,滿足獨立性公理。

(2)

(3)

式中：1為強相關;0為弱相關或不相關;

由式(2)、(3)可知,布料包裝設備用的翻折機構設計屬于非耦合設計,符合獨立性公理,其每個設計細節都是設備設計與生產的理論指導。翻折機構的結構設計方案：凸輪作為運動輸出單元來提供翻折動力,配合推桿連接翻折連桿和翻折板構成兩側對稱結構以避免翻折工作中的干涉問題;限定整個機構垂直方向高度來滿足操作的舒適性要求;針對不同布料幅寬采用伸縮桿來進行適配;對翻折板的轉角、角速度和角加速度進行具體的設計分析,以保證翻折過程平穩。布料包裝設備用的翻折機構工作過程：通過電機驅動凸輪轉動,在推程階段,推桿向上運動并連接翻折連桿實現翻折板相對轉動,完成布料的翻折;當凸輪運轉到回程階段,推桿向下運動,翻折板相背轉動處于復位階段直至回到初始狀態,此過程中翻折板與布料脫離;凸輪處于休止階段時,人工對布料的翻折效果及設備運轉狀態進行審查。

3 翻折機構結構設計分析

在滿足公理化設計準則的前提下,本文設計的翻折機構具體用于布料包裝領域,以彌補該領域的欠缺。該翻折機構選用凸輪機構使得從動件實現間歇往返運動,再串聯連桿機構完成工作,整體機構示意如圖4所示。

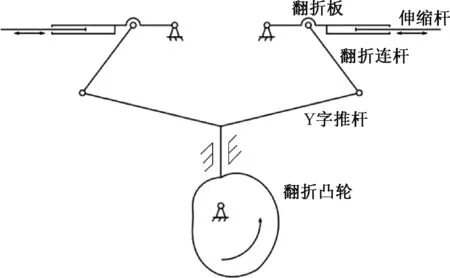
圖4 翻折機構示意圖Fig.4 Diagram of folding mechanism

整個機構由翻折凸輪、Y字推桿、翻折連桿、翻折板和伸縮桿組成。凸輪運動可實現兩側翻折板對向運動,以完成布料的翻轉與折疊。翻折板上安裝的伸縮桿可適應不同幅寬的布料。翻折機構左右兩側為對稱結構,因此只選取右側結構進行設計分析。由圖4可知,翻折機構為由凸輪機構和曲柄滑塊機構串聯而成的六連桿機構,其中滑塊行程距離即為凸輪從動件的推程高度。綜上所述,本文先設計曲柄滑塊機構相關結構,再確定凸輪機構中從動件的運動規律來設計凸輪機構。

3.1 曲柄滑塊機構設計

以右側結構翻折板轉動中心為原點建立直角坐標系,轉動中心到翻折連桿鉸接點的連桿為OA,翻折連桿為AB,Y字推桿轉換為滑塊,故翻折機構中連桿機構即等效為曲柄滑塊機構,如圖5所示。給定OA桿長為l1,AB桿長為l2,OA、AB與x軸正向夾角分別為φ1、φ2,偏距(曲柄回轉中心與滑塊移動導路的偏置距離BC)為e,OC桿長為l,其中Ai與Bi(i=1,2,3)為3個不同時刻A點與B點位置之間的3組對應關系。

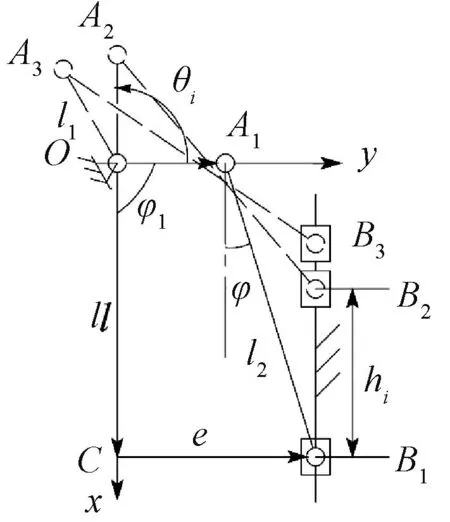
圖5 曲柄滑塊機構示意圖Fig.5 Crank slider mechanism schematic

由封閉四邊形OABC各矢量方向得封閉矢量方程如式(4)所示。

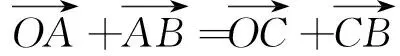
(4)

分別取實部和虛部得：

(5)

由式(5)可得

(6)

故B點坐標為

為探究翻轉板轉動角度與布料位置狀態的關系,本文以翻轉板轉動90°為起點,依次增加5°(直至120°)進行試驗,相關試驗結果如表4所示。由表4可知,當轉角大于115°時可實現布料的翻折。

表4 翻轉板轉角與布料狀態關系Table 4 Turning angle of floding plate and fabric state relationship

結合整機尺寸高度設定翻折板轉角θi與推桿位移hi(i=1,2,3)之間的3組對應關系：θ1=0,h1=0 mm;θ2=π/2,h2=79.97 mm;θ3=2π/3,h3=159.94 mm。如圖5所示,A1B1、A2B2、A3B3分別為翻折連桿的3處位置,而θi為OAi與y軸正向的夾角。

利用位移矩陣法[12-13],得出OA的位移矩陣

(7)

則A點的位置方程為

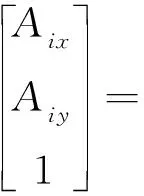
(8)

而B點做上下往復運動,其坐標方程為

(9)

且AB桿長不變,故由定長條件,得約束方程

(Aix-Bix)2+(Aiy-Biy)2=

(A1x-B1x)2+(A1y-B1y)2

(10)

企業生產過程中,包裝前的面料須經碼布機進行前處理,而碼布機最終的出料平臺距離地面750 mm,該高度符合企業操作工人搬運習慣,因此設為布料折疊包裝機承接布料的高度,即機構空間配合高度OA=60.0 mm,聯立式(7)～(10),解得翻折連桿AB為300.0 mm,滑塊偏距By為240.0 mm。

3.2 凸輪廓線設計

結合實際生產工況要求,機構適用于中高速勻速重載,實現布料翻折時間為1～2 s,故設定翻轉凸輪的轉速為25 r/min,且逆時針轉動。凸輪機構在推程階段實現布料的翻折,而回程階段則為機構的復位。為提升工作效率,凸輪機構回程階段時間不應過長,同時增加休止階段來完成布料翻折效果與設備運轉狀態的審查工作,按表5所示分配凸輪轉角與從動推桿的運動行程關系。

表5 凸輪轉角與運動相位配合關系

在推程階段,需保證布料不因受到沖擊而散落,因此在凸輪給恒定轉速的情況下選用幾種常見的凸輪從動件運動規律來研究翻折板的運動情況[14]。圖6和圖7為不同凸輪在動件運動規律下,翻折板的角速度與角加速度變化。由圖6和圖7可知：除等速運動規律外,其余幾種運動規律的推程過程中,翻折板的角加速度都發生了變化,且角速度峰值位置位于翻折過程中,這勢必會造成布料散落,因此凸輪推程部分選用等速運動規律,翻折過程的翻折板角速度與角加速度變化平穩,更利于布料的翻折。

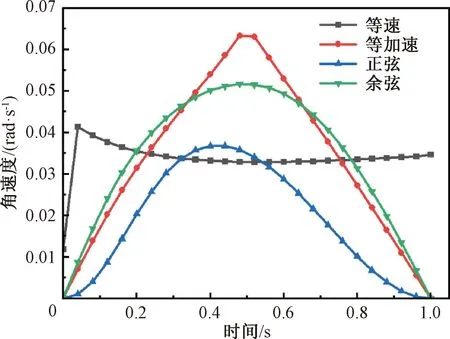
圖6 不同從動件運動規律下翻折板角速度Fig.6 Angular velocity of folding plate under different follower motion laws

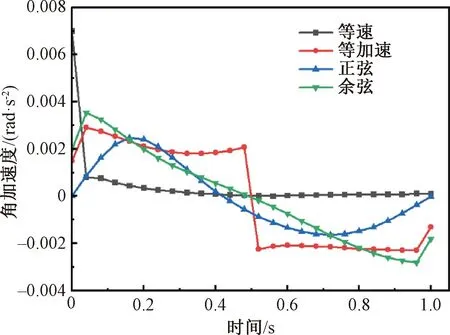
圖7 不同從動件運動規律下翻折板角加速度Fig.7 Angular acceleration of folding plate under different follower motion laws

設定凸輪逆時針轉動,轉動角速度為ω,凸輪轉角為δ(弧度制),凸輪推程運動角δ0=5π/6,回程運動角δ′0=2π/3(見表5),推桿上升高度h=160 mm。由于推程階段存在剛性沖擊,因此需在運動始末加以修正,運動回程階段處于空載情況,對運動特性無特殊要求。為減小沖擊,本文在此階段按正弦加速度運動規律來設計凸輪廓線。

當δ∈[0,5π/6)時,推桿推程的運動方程如式(11)所示。

(11)

當δ∈[5π/6,3π/2)時,推桿回程的運動方程如式(12)所示。

(12)

當δ∈[3π/2,2π]時,推桿處于休止階段,其位移、速度、加速度均為零。

因布料包裝設備整機高度有限,且大尺寸凸輪會消耗更大能量,在滿足凸輪機構壓力角小于許用壓力角的前提下,為更好地設計與裝配,設定基圓半徑R=100 mm,再利用式(11)～(12)結合反轉解析法[15]得到凸輪的輪廓曲線,同時為避免推程始末的剛性沖擊,對所繪制的凸輪廓線[16]在運動不同階段的連接處做修整處理,如圖8所示。經修整后,翻折板在推程階段運行的剛性沖擊得到明顯改善,推程階段翻折板修整前后的加速度變化如圖9所示。

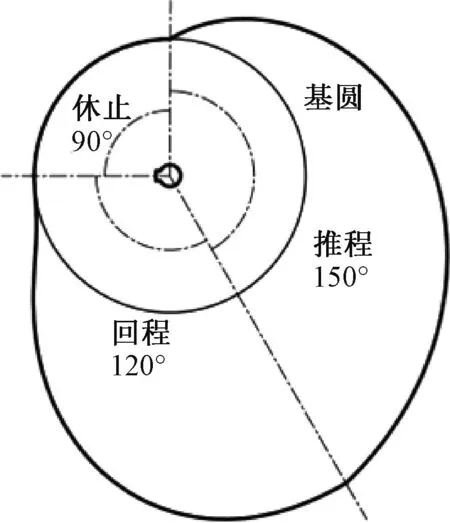
圖8 翻折凸輪輪廓曲線Fig.8 Profile curve of the folding cam

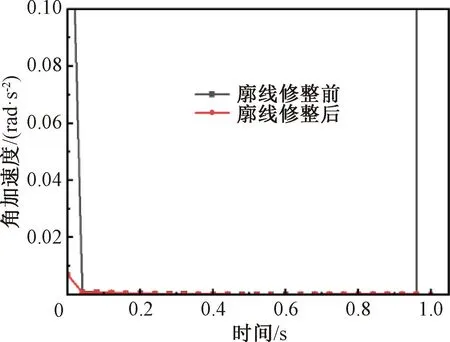
圖9 翻折板修整前后的加速度變化Fig.9 Variation of angular acceleration of folding plate during the pushing phase before and after trimming

4 運動仿真分析

創建翻折機構的模型,使用Motion插件進行運動仿真分析[17-19]。其中,Y字推桿與左右翻折連桿鉸接點的水平距離為980 mm,且該鉸接點至Y字推桿與凸輪的接觸點垂直高度為300 mm,其余各構件尺寸根據前述結構設計構建。1個翻折周期即凸輪轉動1周,凸輪與推桿為正偏置裝配,可以更好地傳動。仿真時間設置為2.4 s,可得到翻折板的運動尺度的變化如圖10～11所示。

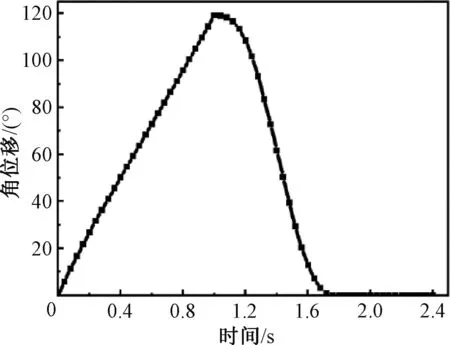
圖10 翻折板角位移變化Fig.10 Variation of angular displacement of folding plate

由圖10可知,翻折板的角位移隨時間變化呈先上升后下降再穩定的趨勢,且最大轉角位置在1 s處,即凸輪轉動150.00°。推程結束翻折板翻轉最大角度為119.11°,與設計條件偏差0.74%,這并不影響實際生產,故該機構設計能夠實現指定的動作需求。

由圖11可知,凸輪的推程階段除在開始時存在沖擊外,其余過程中的翻折板角速度與角加速度均變化平穩;推程結束時角速度和角加速度由于凸輪從動件運動規律變化而產生了突變,此處剛好布料與翻折板脫離,故不會影響翻折效果。回程階段角速度與角加速度符合正弦運動規律,滿足慢進快回的設計要求。因此,該翻折機構的運動特性滿足結構設計需求并符合實際生產情況。

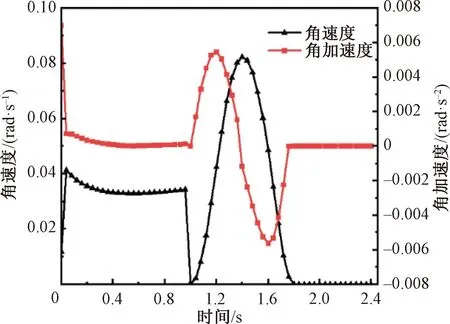
圖11 翻折板角速度、角加速度變化Fig.11 Variation of angular velocity and angular acceleration of folding plate

5 結 論

1)采用公理化設計理論,從用戶域、功能域、結構域進行翻折機構的功能特性和設計需求的分析,結合獨立性公理,證明了翻折機構的功能特性與設計需求分解是非耦合設計,并提出曲柄滑塊機構和凸輪機構串聯而成的六桿機構作為翻折機構的結構方案。

2)分析翻折機構的滑塊與位置與曲柄轉角的關系,根據位置矩陣分析設計出曲柄滑塊機構的尺寸參數。對比多種從動件運動規律,結合翻折板運動特性,設計出推程為等速運動規律、回程為正弦運動規律的凸輪。

3)利用Motion對翻折機構模型進行一個周期的運動仿真,得到翻折板最大角位移與設計要求偏差僅為0.74%,且角速度和角加速度變化不會對布料翻折效果造成影響,符合實際生產工況要求。