學案導學教學模式在初中數學教學中的實踐與研究

孫彩平

【摘要】學案導學教學法在教育改革背景下受到教育工作者的廣泛關注.學案是教師依據教學目標以及學生的知識結構，設計用于學習使用的方案，包含學習目標、重難點及學法指導等內容，可以突出學生在學習中的主體地位，幫助學生養成良好的自學習慣.為發揮學案導學的優勢，本文由學案導學內涵以及在初中數學教學中的實踐價值出發，從“依標設計，依案導學、集中討論，嘗試解疑、精講點撥，總結歸納、知識拓展，創造應用”等角度出發，總結學案導學的具體使用方法，意在促進教師教學方式以及學生學習方式的變革，構建更具智慧的數學課堂.

【關鍵詞】學案導學；初中數學；教學實踐

學案是根據教學目標、學生的知識構架以及學習能力設計的可以提供給學習者使用的學習方案.學習方案的設計，包含了基本教學目標、課題探究，還包括解題思路、指導學習方法以及提升解題能力、歸納總結知識要點.目前，部分學生在參與初中階段數學學習過程中，存在學習興趣不足、難以構建知識體系等現象.為解決這一問題，教師可以借助學案導學的優勢，利用學案為引導，有效幫助學生在學案導學中獲取知識，提高自身核心素養.

1 學案導學內涵以及在初中數學教學中的實踐價值

為實現理想化的教育目標，教師需要深刻把握學案導學的具體內涵.通過對相關文獻的閱讀與分析，筆者將學案以及導學進行拆分論述：學案導學是以學案為載體，以導學為方法，由師生共同合作完成教學任務的一種教學模式，在這種模式下教師起到指導作用，學生作為主體，體現了和諧、良性的師生關系.實施學案導學教學法具有重要價值：第一，學案導學體現了先學后教的思想，教師根據教學內容以及學生學習能力設計導學方案，并引導學生運用已有知識進行思考、探索，最終掌握知識規律，在這個過程中教師只需要在學生出現學習困惑時給予適度指導，這樣“學會放手”的教學方式，可以推動學生學習方式的轉變，在潛移默化中學生也將逐漸由被動接受知識轉為主動汲取知識，對學生自主學習能力的形成具有重要價值.第二，學案導學教學法始終將教學活動的重心放在“學生的學”上，突破傳統機械化、單一化教學模式的弊端，在問題解決過程中，學生的主體地位將得到充分提升，教師也能從中積累經驗，促進教與學的雙向發展，幫助學生活躍思維，提高學生核心素養.第三，學案的設計不僅體現了新的教育理念，同時也具有明顯的創新性、導向性以及實踐性，學生在獨立思考、分析后，需要對共同存在的問題進行集中討論，在討論過程中，學生不僅能建立良好的合作學習意識，同時也能逐步提高自身問題解決能力，為后續參與高中階段數學學習奠定堅實的基礎.第四，學案導學教學模式突破了傳統的教學結構，按照引入學案—嘗試自學—暴露問題—合作解決—探究規律的順序進行，充分體現了學生自主學習的過程，在良好的課堂氛圍中，學生自學自悟，教師導學導悟，能有效實現雙向發展.

由此可見，在初中數學教學中實施學案導學，能有效提高教學質量，提高學生分析問題與解決問題的基本能力.對此，要想提高初中數學教學質量，教師需要關注學案導學的具體內涵，結合學科特色合理設計，借此實現理想化的教育目標.

2 學案導學教學模式在初中數學教學中的實踐策略

學案導學的設計需要兼顧學生個性化差異以及課型與知識類型，科學設計才能突出其使用價值.以下為筆者對學案導學模式的一些思考，期望為廣大教師提供幫助.

2.1 依標設計，依案導學

學案的設計需要緊密依靠目標，因此在準備階段，教師需要深入研讀教材內容，明確本課重點目標再根據學生學習能力進行合理設計，突出重點、難點，為學生后續學習奠定基礎.

例如 以魯教版七年級上冊“一次函數”一課教學為例，本課為函數知識的基礎，學生需要通過學習掌握一次函數以及正比例函數.在課前階段，教師首先對教材內容進行梳理，并根據學生在函數這一章節中的學習表現作出判斷，據此明確教學目標：（1）幫助學生通過學習掌握一次函數和正比例函數的概念，并能夠根據具體情境判斷一次函數的表達方式.（2）經歷一次函數概念的抽象概括過程，拓寬自身抽象思維能力.在教學目標設計完畢后，教師可以利用導學案為學生分享課前預習內容，指導學生在學案的指引下參與自主預習（表1）.

如上，根據教學目標為學生設計導學案，指導學生根據導學案內容參與自主預習的方式，可以充分突出導學案的“導學”優勢，幫助學生在自主預習中初步掌握本課重點內容，為后續活動開展奠定基礎.

2.2 集中討論，嘗試解疑

在概念生成環節，利用導學案能幫助學生梳理基礎概念知識，幫助學生加深對關鍵詞的印象.導學案中還包含了問題板塊，學生需要基于對概念知識的理解自主解決問題，或是結合導學案內容自主提出問題.在提問環節中，教師可以采用集中討論的方式，指導學生對導學案中的問題進行分析、探究，在思考中提供自身問題解決能力.

例如 以魯教版八年級上冊“分式的加減法”一課教學為例，導學案中為學生提供了清晰的學習目標，要求學生在本課學習中掌握類比同分母分數加減法猜想同分母分式的加減法則，并能夠在具體問題中利用同分母分式進行加減法計算.為考查學生的問題解決能力，教師結合重點內容并聯系生活實際為學生設計了這樣一道問題：周末小剛從家騎車前往3千米處的奶奶家，再以同樣的速度騎車到距離奶奶家2千米的新華書店，假設小剛騎車的速度為v千米/小時，請問小剛從家到奶奶家花費了多長時間？從奶奶家再到新華書店花費了多長時間？小剛從家到新華書店的路上一共用了多長時間？根據導學案中的問題，學生以小組為單位進行交流，本道題目為行程問題，根據路程=速度×時間，學生給出答案分別為：3/vh、2/vh、（3/v+2/vh）.接下來，為發展學生高階思維，教師可以在原有導學案上，指導學生根據此問題自主設計并提出自己的疑問與思考：同分母的分數加減法和整數加減法是否相同？假如分母不同又應如何進行計算？隨后，教師再匯總問題指導學生填寫在導學案上，不斷完善、補充導學案內容.

如上，利用學案問題引導學生進行集中討論，并鼓勵學生自主設計新問題的方式，可以充分凸顯學生在學習活動中的主體地位，使學生通過思考發展自身思維能力，達成預期教學目標.

2.3 精講點撥，總結歸納

在利用學案帶領學生分析問題、解決問題的過程中，部分學生因個體化差異對知識的理解程度存在顯著差別.針對這一問題，教師需要實時監控學生學案習題練習情況，有針對性地對學生存在的共性問題進行解答，并指導學生從問題中尋找規律，利用思維導圖的方式進行總結歸納.這樣，既能保障班級內學生的參與程度，同時也能使學生借助學案構建完整的知識框架，提高整體課堂教學質量.

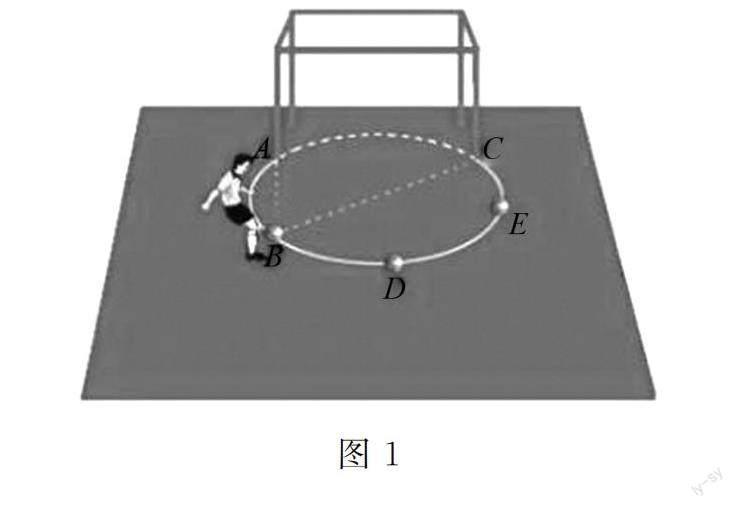
例如 以魯教版九年級下冊“圓周角和圓心角的關系”一課教學為例，在本課學習中，學生需要掌握圓周角的概念以及圓周定理，并能夠在具體情境中運用所學知識解決圓有關的問題.導學案中教師為學生設計了重點問題：圓心角的定義是什么？圓心角的度數和它所對的弧的度數有什么關系？如何判斷圖形中的角是否為圓周角？在學生歸納整理的過程中，教師發現部分學生極容易將二者混淆，且對圓周角與圓心角之間的關系理解得不夠透徹.針對這一問題，教師可以拓展導學案內容，為學生進行精講點撥.為便于學生理解，教師可以利用足球比賽中的射門作為情境（圖1）.

引導學生思考圖中∠ABC的頂點各在圓的什么位置？∠ABC的兩邊和圓是什么關系？根據真實情境，學生可以通過數學模型的建立得出結論，深刻地認識到頂點在圓上且角的兩邊分別和圓另有交點的角為圓周角.再仿效此種方法，教師可以指導學生自己整理圓心角定義，并利用思維導圖的方式進行呈現，記錄在導學案中，在班級中分享自己的設計內容，營造良好的學習氛圍，幫助學生在總結歸納中得到升華.

如上，導學案不僅能夠利用于課前預習，教師同樣可以指導學生參與到導學案設計中，利用思維導圖的方式歸納總結重點內容，有效幫助學生提高學習質量.

2.4 知識拓展，創造應用

在基礎教學任務結束后，為加深學生對知識的理解程度，教師可以再次引入導學案，為學生分享本課練習題目，引導學生結合所學知識解決問題.凝結了重點知識內容的練習題，可以幫助學生進行系統性的整理回顧，在變式訓練中發展學生思維能力，提高解題效率.

例如 以魯教版七年級下冊“解二元一次方程組”一課教學為例，在本課學習中學生已經掌握了運用代入消元法解決二元一次方程組的基本方法，在課后總結復習階段，教師為大家設計復習導學案，指導學生完成導學案中的練習題目.

“解二元一次方程組”課內檢測：

（1）我國古代數學著作《孫子算經》中有雞兔同籠問題：今有雞兔同籠，上有三十五頭，下有九十四足，問雞兔各幾何.用二元一次方程組解決問題.

（2）把一根長7m的鋼管截成2m長和1m長兩種規格的鋼管，怎樣截不造成浪費？你有幾種不同的截法？

（3）有48支隊520名運動員參加籃球、排球比賽，其中每支籃球隊10人，每支排球隊12人，每名運動員只能參加一項比賽，問各有多少支籃球、排球隊參賽？

以上題目能考查學生對知識的理解程度，根據學生解答問題的情況，教師可以有針對性地調整后續導學案內容，以便于發揮導學案優勢價值，促進學生全面發展.

如上，將學案用于課后復習環節，可以幫助學生通過任務練習鞏固深化所學知識，指導學生學習方向，幫助其在訓練中發展自身思維能力，為后續參與高中階段數學學習儲備能量.

3 結語

綜上所述，學案的應用能充分提高學生主體性學習地位，發揮導學優勢，在激發學生學習興趣的同時，使其借助學案養成良好自主探究與學習習慣.因此，在初中數學教學中，教師需要關注學案的導學價值，并結合學生思維能力合理設計，提高學案設計的有效性，推動學生核心素養發展.在廣大教師的努力下，初中數學教學質量也將得到質的提升.

參考文獻：

[1]郭格秀.以“導”為中心——談初中數學導學案的設計策略[J].數學教學通訊，2022（35）：78-79.

[2]李成煒.學案式教學模式在初中數學教學中的運用[J].數學學習與研究，2022（33）：137-139.

[3]唐燕.深度教學，導學案先行——基于導學案的初中數學教學實踐策略[J].新課程教學（電子版），2022（15）：87-88.

[4]黃菁菁.初中數學“導學案”教學模式下如何培養學生的自主學習能力[J].中學數學，2022（12）：92-93.

[5]吳宗繩.差異化教學在初中數學教學中的運用[J].中學課程輔導，2023（14）：36-38.