分布式動(dòng)力翼前飛狀態(tài)動(dòng)力/氣動(dòng)耦合特性

王科雷，周洲，郭佳豪，李明浩

西北工業(yè)大學(xué) 航空學(xué)院，西安 710072

提高飛行效率、降低燃油消耗率是飛行器設(shè)計(jì)追求的永恒目標(biāo)之一。面對(duì)未來(lái)航空器高經(jīng)濟(jì)性、低能耗、低噪聲和低污染的“綠色航空”［1］發(fā)展需求，世界各航空大國(guó)均已規(guī)劃了各自的發(fā)展藍(lán)圖［2-4］，其中，美國(guó)國(guó)家航空航天局（National Aeronautics and Space Administration， NASA）的“N+3”計(jì)劃［5］指出，到2035 年商業(yè)民用客機(jī)的燃油消耗率要再降低60%。顯然，為了實(shí)現(xiàn)這一宏大目標(biāo)，需要在包括氣動(dòng)、結(jié)構(gòu)、控制以及動(dòng)力等多個(gè)技術(shù)領(lǐng)域內(nèi)有所突破，其中，動(dòng)力系統(tǒng)革新尤為受關(guān)注。在眾多創(chuàng)新概念中，分布式混合推進(jìn)系統(tǒng)技術(shù)展現(xiàn)出了明顯的發(fā)展?jié)摿ΓM管目前仍在電力儲(chǔ)能、電推進(jìn)系統(tǒng)等方面存在技術(shù)瓶頸，但是新型推進(jìn)方式的變革體現(xiàn)了飛行器設(shè)計(jì)從單一動(dòng)力研究到飛行器總體、動(dòng)力、氣動(dòng)等技術(shù)集成研究的變化，很有可能成為航空工業(yè)的革命性轉(zhuǎn)折，為航空科技發(fā)展提供新的方向［6-7］。

分布式混合電推進(jìn)系統(tǒng)是指通過傳統(tǒng)燃?xì)鉁u輪發(fā)動(dòng)機(jī)為分布在機(jī)翼或機(jī)身的多個(gè)電機(jī)/風(fēng)扇提供電力，并由電機(jī)驅(qū)動(dòng)風(fēng)扇提供絕大多數(shù)或全部推力的一種新型推進(jìn)系統(tǒng)概念。與傳統(tǒng)動(dòng)力推進(jìn)相比，分布式混合電推進(jìn)系統(tǒng)具備高可靠、易分配、尺度無(wú)關(guān)等特性［8-9］，其布置更加高效靈活，與飛行器機(jī)體融合度顯著提高，可以有效改善原有飛行器結(jié)構(gòu)、大幅提高等效涵道比、降低油耗及減少噪聲和排放，在軍民航空領(lǐng)域均極具應(yīng)用價(jià)值，目前已引起了世界各大航空研發(fā)機(jī)構(gòu)的高度重視，而隨著國(guó)內(nèi)外圍繞分布式動(dòng)力/機(jī)翼耦合設(shè)計(jì)問題的研究工作逐漸增多，已形成部分認(rèn)識(shí)，并引發(fā)了動(dòng)力/氣動(dòng)設(shè)計(jì)理念的革新［10-14］。

現(xiàn)有分布式混合電推進(jìn)飛行器整體上可以歸結(jié)為3 種基礎(chǔ)氣動(dòng)布局形式：① 翼前/翼后分布式動(dòng)力，機(jī)翼翼面完全處于動(dòng)力噴流流管內(nèi)，或動(dòng)力處于機(jī)翼尾跡流場(chǎng)內(nèi)，如美國(guó)X-57 飛機(jī)；② 翼上/翼下分布式動(dòng)力，機(jī)翼翼面局部受到動(dòng)力抽吸和噴流誘導(dǎo)，而機(jī)翼外部流動(dòng)形態(tài)亦對(duì)動(dòng)力工作狀態(tài)有所影響，如德國(guó)Lilium Jet“百合”垂直起降飛機(jī)、美國(guó)NASA N3-X 通用客機(jī)；③ 分布式動(dòng)力翼（Distributed-Propulsion-Wing， DPW），內(nèi)外流完全摻混，動(dòng)力即機(jī)翼，機(jī)翼即動(dòng)力，如美國(guó)XV-24“雷擊”垂直起降無(wú)人機(jī)。其中前2 種氣動(dòng)布局形式相對(duì)常規(guī)，可以借鑒傳統(tǒng)思路和方法進(jìn)行氣動(dòng)外形設(shè)計(jì)，但第3 種分布式動(dòng)力翼布局形式已然打破了傳統(tǒng)飛發(fā)匹配概念，實(shí)現(xiàn)了分布式動(dòng)力與機(jī)翼氣動(dòng)面的完全融合，這為飛行器高效設(shè)計(jì)帶來(lái)極大的空間，但同時(shí)也帶來(lái)極大的復(fù)雜度和困難，亟須圍繞其動(dòng)力/氣動(dòng)耦合特性開展詳細(xì)分析研究，進(jìn)而為后續(xù)開展動(dòng)力/氣動(dòng)一體化設(shè)計(jì)提供理論支撐，這是本文主要關(guān)注點(diǎn)。

對(duì)于涵道風(fēng)扇問題，目前主要圍繞數(shù)值求解方法［15-17］、槳葉設(shè)計(jì)［18-20］和氣動(dòng)特性分析［21-23］3 個(gè)方面展開。而對(duì)于分布式涵道風(fēng)扇問題，目前主要關(guān)注由動(dòng)力分布帶來(lái)的圓形和方形涵道唇口影響［24-25］、翼上分布式涵道風(fēng)扇邊界層抽吸效應(yīng)［26-30］以及從動(dòng)力、氣動(dòng)單學(xué)科出發(fā)的考慮機(jī)翼安裝約束的分布式涵道風(fēng)扇進(jìn)氣道設(shè)計(jì)［31］、考慮分布式排布的涵道風(fēng)扇動(dòng)力單元懸停/平飛多目標(biāo)設(shè)計(jì)［32］和耦合分布式涵道風(fēng)扇的機(jī)體氣動(dòng)布局設(shè)計(jì)［33］。總的來(lái)說(shuō)，現(xiàn)有研究主要針對(duì)涵道風(fēng)扇內(nèi)流特性及其對(duì)機(jī)翼外部流動(dòng)的氣動(dòng)影響展開，對(duì)于涵道外壁直接充當(dāng)氣動(dòng)面的問題鮮有研究。

因此，本文以類美國(guó)XV-24“雷擊”垂直起降無(wú)人機(jī)布局的分布式動(dòng)力翼為研究對(duì)象，首先開展分布式動(dòng)力翼參數(shù)化建模方法研究，通過程序?qū)崿F(xiàn)復(fù)雜曲面自動(dòng)造型。然后，基于計(jì)算流體力學(xué)（Computational Fluid Dynamics，CFD）方法，使用商業(yè)軟件FLUENT，由動(dòng)力翼二維剖面翼型到動(dòng)力翼單元翼段，再到分布式動(dòng)力翼整體依次進(jìn)行數(shù)值模擬及動(dòng)力/氣動(dòng)耦合特性分析，從設(shè)計(jì)角度考慮，XV-24 鴨式布局俯仰力矩配平能力較強(qiáng)，因此重點(diǎn)關(guān)注分布式動(dòng)力翼的升阻特性與推進(jìn)特性。最后，對(duì)分布式動(dòng)力翼內(nèi)外流耦合與其動(dòng)力/氣動(dòng)耦合特性變化之間關(guān)系進(jìn)行歸納總結(jié)，同時(shí)提出對(duì)分布式動(dòng)力翼動(dòng)力/氣動(dòng)一體化設(shè)計(jì)思路的建議。

1 分布式動(dòng)力翼參數(shù)化建模方法

參考美國(guó)XV-24“雷擊”垂直起降無(wú)人機(jī)布局形式，構(gòu)建如圖1 所示包含6 個(gè)涵道風(fēng)扇的分布式動(dòng)力翼半展長(zhǎng)模型作為設(shè)計(jì)對(duì)象進(jìn)行分析研究。該分布式動(dòng)力翼可以按照“方-圓-方”動(dòng)力翼單元進(jìn)行劃分，各動(dòng)力翼單元核心為包含轉(zhuǎn)子、槳轂、涵道筒的轉(zhuǎn)動(dòng)部件（Rotor Compo?nent）、“方-圓”進(jìn)氣道（Inlet）和“圓-方”排氣道（Outlet），外壁采用常規(guī)機(jī)翼上下翼面作為動(dòng)力翼外翼面（Duct-wing）。研究過程中始終保持轉(zhuǎn)子及槳轂的幾何模型固定不變，分別對(duì)涵道筒、“方-圓”進(jìn)氣道、“圓-方”排氣道和動(dòng)力翼外翼面進(jìn)行參數(shù)化建模。這里，考慮涵道筒幾何型面相對(duì)簡(jiǎn)單，僅采用涵道筒半徑R及其長(zhǎng)度lhd進(jìn)行描述，此處不再贅述。此外，為了便于分析，擬排除因動(dòng)力內(nèi)流特征變化而產(chǎn)生對(duì)動(dòng)力翼外流特征及升阻特性帶來(lái)的影響，采用單一變量法，對(duì)動(dòng)力翼內(nèi)壁面進(jìn)行簡(jiǎn)化處理。一方面在對(duì)比分析過程中保持動(dòng)力翼內(nèi)壁面及轉(zhuǎn)動(dòng)部件模型始終不變；另一方面約束進(jìn)、排氣道曲面始終沿垂向上下、沿展向左右對(duì)稱，進(jìn)而在一定程度保證來(lái)流狀態(tài)改變時(shí)，動(dòng)力翼氣動(dòng)特性變化僅與外翼面模型參數(shù)相關(guān)聯(lián)。

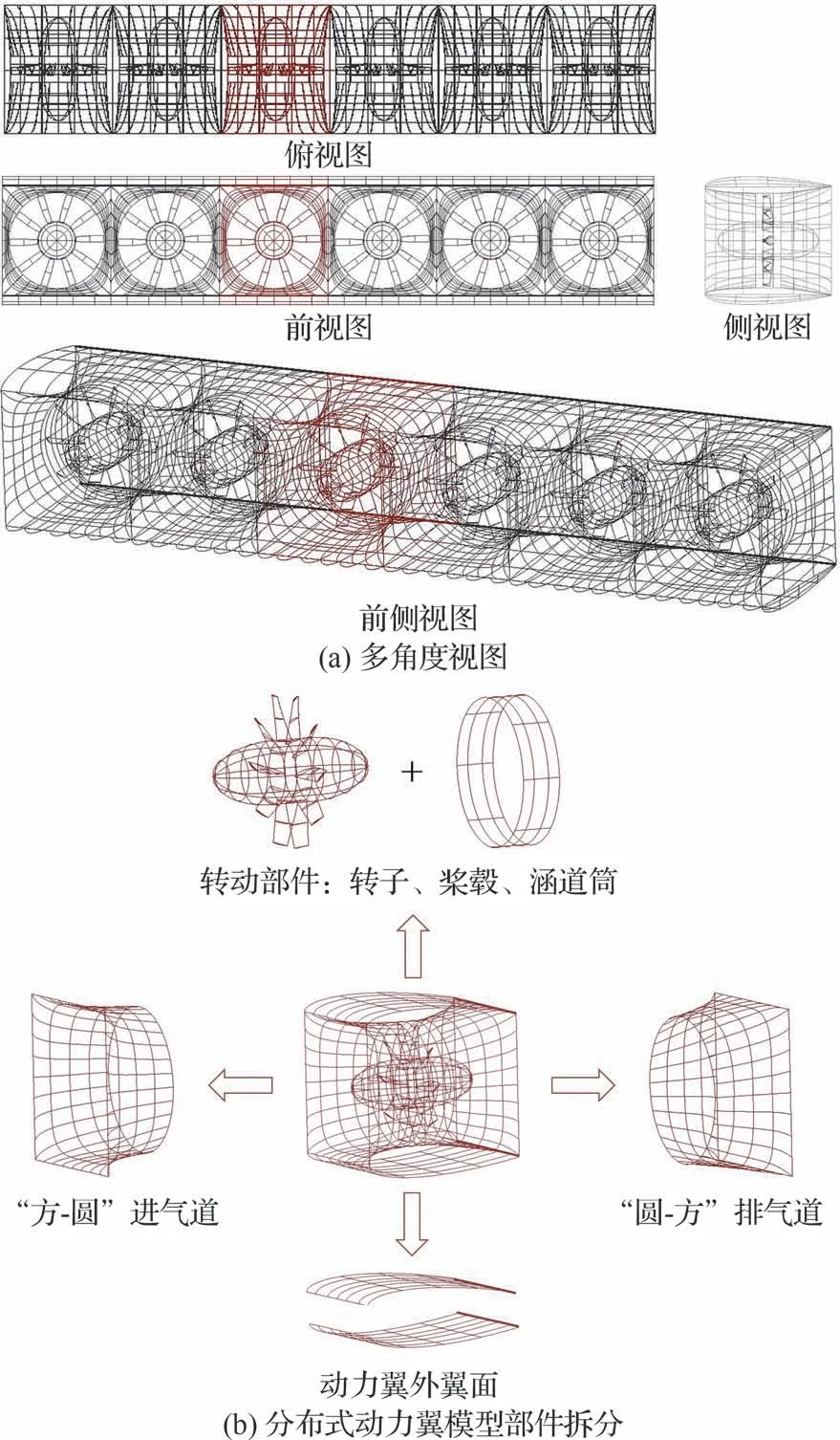
圖1 分布式動(dòng)力翼半展長(zhǎng)模型對(duì)象Fig.1 Distributed-propulsion-wing half-span model object

1.1 “方-圓”進(jìn)氣道參數(shù)化建模

“方-圓”進(jìn)氣道為上下、左右對(duì)稱曲面，僅需對(duì)其1/4 外形進(jìn)行參數(shù)化即可［31］。如圖2 所示，該“方-圓”進(jìn)氣道主要外形參數(shù)包括進(jìn)口高度hin、進(jìn)口寬度bin、進(jìn)口長(zhǎng)度lin、涵道筒半徑R。為了實(shí)現(xiàn)進(jìn)氣道由方形到圓形的曲面過渡，采用超橢圓方程［34-35］對(duì)其沿流向截面輪廓進(jìn)行參數(shù)化：

圖2 “方-圓”進(jìn)氣道模型Fig.2 “Square-Circle” inlet model

式中：a為超橢圓長(zhǎng)半軸；b為超橢圓短半軸；m為超橢圓指數(shù)。當(dāng)m=2 時(shí)超橢圓方程即為橢圓方程，當(dāng)m＞2 且m不斷增大時(shí)，橢圓逐漸向矩形過渡。因此，對(duì)于圖2 所示“方-圓”進(jìn)氣道而言，其方形進(jìn)口輪廓的超橢圓方程參數(shù)為a=bin/2、b=hin/2、m=+∞，其圓形出口輪廓的超橢圓方程參數(shù)為a=R、b=R、m=2。

進(jìn)一步采用四階Bezier 曲線［36］對(duì)進(jìn)氣道脊線a（t）、b（t）、m（t）進(jìn)行參數(shù)化：

式中：t為控制參數(shù)，t=0～1；（x，ya）、（x，yb）、（x，ym）分別為進(jìn)氣道脊線a（t）、b（t）、m（t）的坐標(biāo)。a（t）曲線控制截面輪廓的超橢圓長(zhǎng)半軸變化，對(duì)應(yīng)控制點(diǎn)為（p1，p6）、（p2，p7）、（p3，p8）、（p4，p9）、（p5，p10）；b（t）曲線控制截面輪廓的超橢圓短半軸變化，對(duì)應(yīng)控制點(diǎn)為（p1，p11）、（p2，p12）、（p3，p13）、（p4，p14）、（p5，p15）；m（t）曲線控制超截面輪廓的橢圓指數(shù)變化，對(duì)應(yīng)控制點(diǎn)為（p1，p16）、（p2，p17）、（p3，p18）、（p4，p19）、（p5，p20）。

為保證涵道曲面的光滑連續(xù)，令進(jìn)氣道方形進(jìn)口處控制曲線與涵道外壁面垂直相接，進(jìn)氣道圓形出口處控制曲線與涵道筒水平相接。根據(jù)Bezier 曲線端點(diǎn)性質(zhì)及導(dǎo)數(shù)性質(zhì)可知

由此該“方-圓”進(jìn)氣道曲面的實(shí)際控制變量共8 個(gè)：p2、p3、p8、p9、p13、p14、p18、p19。

進(jìn)一步根據(jù)幾何參數(shù)對(duì)控制變量進(jìn)行單位化處理，令

此時(shí)四階Bezier 曲線x′（t）、y′a（t）、y′b（t）、y′m（t）對(duì)應(yīng)的控制變量為

當(dāng)確定a（t）、b（t）、m（t） 3 條控制曲線后，超橢圓的長(zhǎng)短半軸信息可直接根據(jù)對(duì)應(yīng)的Bezier曲線求得。而超橢圓指數(shù)m則根據(jù)曲線m（t）求解得到。設(shè)曲線m（t）對(duì)應(yīng)的高度hm（t）和bm（t）分別為

在已知ya（t）、yb（t）和ym（t）后，根據(jù)式（19）～式（21）即可求得對(duì)應(yīng)的超橢圓指數(shù)m，繼而自動(dòng)生成相應(yīng)的“方-圓”進(jìn)氣道曲面。

1.2 “圓-方”排氣道參數(shù)化建模

與“方-圓”進(jìn)氣道類似，“圓-方”排氣道采用如圖3 所示外形參數(shù)和a*（t）、b*（t）、m*（t）曲線進(jìn)行定義。其主要外形參數(shù)包括出口高度hout、出口寬度bout、出口長(zhǎng)度lout、涵道筒半徑R。對(duì)于動(dòng)力翼單元而言，排氣道出口寬度bout與進(jìn)氣道進(jìn)口寬度bin相等，即bout=bin。

圖3 “圓-方”排氣道模型Fig.3 “Circle-Square” outlet model

a*（t）、b*（t）、m*（t）曲線控制方程如下：

進(jìn)一步根據(jù)幾何參數(shù)對(duì)控制變量進(jìn)行單位化處理，令

為保證涵道曲面的光滑連續(xù)，令排氣道圓形進(jìn)口處控制曲線與涵道筒水平相接，排氣道矩形出口末端保持水平。根據(jù)Bezier 曲線端點(diǎn)性質(zhì)及導(dǎo)數(shù)性質(zhì)可知

1.3 動(dòng)力翼外翼面參數(shù)化建模

考慮動(dòng)力翼外翼面采用常規(guī)機(jī)翼上下翼面，因此采用CST（Class Function/Shape Function Transformation）參數(shù)化方法［37］分別對(duì)上、下曲面的翼型輪廓進(jìn)行參數(shù)化建模，上、下翼型具體表達(dá)式如下：

式中：yTu和yTl分別為翼型上下表面后緣（Trail?ing Edge， TE）的y軸坐標(biāo)；C（x）為類函數(shù)；Su（x）及Sl（x）為型函數(shù)。

類函數(shù)C（x）中，對(duì)于一般翼型取N1=0.5、N2=1。Aui和Ali為控制點(diǎn)，N為Si（x）的階數(shù)，這里取N=6。由此動(dòng)力翼外翼上、下表面各有7 個(gè)控制變量。

1.4 分布式動(dòng)力翼模型參數(shù)化描述

綜上，對(duì)于如圖1 所示分布式動(dòng)力翼模型，在保持轉(zhuǎn)動(dòng)部件固定不變的情況下，可以用表1 所列共計(jì)40 個(gè)控制參數(shù)進(jìn)行描述和自動(dòng)曲面造型。

表1 分布式動(dòng)力翼模型參數(shù)定義Table 1 Definitions of distributed-propulsion-wing model parameters

2 數(shù)值模擬方法及計(jì)算模型

2.1 數(shù)值模擬方法

針對(duì)分布式動(dòng)力翼多轉(zhuǎn)子內(nèi)部流動(dòng)與翼面外部流動(dòng)耦合問題，采用耦合k-ω剪切應(yīng)力輸運(yùn)（Shear-Stress Transport， SST）湍流模型［38］求解雷諾平均Navier-Stokes（Reyolds-Averaged Navier-Stokes， RANS）方程的多重參考坐標(biāo)系（Multiple Reference Frame， MRF）準(zhǔn)定常求解方法［39］，使用商業(yè)軟件FLUENT 進(jìn)行數(shù)值模擬研究。數(shù)值計(jì)算過程中空間離散采用二階迎風(fēng)MUSCL（Mono?tone Upstream-Centered Scheme for Conserva?tion Laws）插值的Roe 格式，時(shí)間離散與推進(jìn)則采用隱式AF（Approximate Factorization）方法。其中，k-ωSST 湍流模型是一種得到工程廣泛應(yīng)用的兩方程混合模型，它在遠(yuǎn)離壁面純湍流區(qū)域使用標(biāo)準(zhǔn)k-ε模型計(jì)算，在近壁面區(qū)域保留了適用于各種壓力梯度邊界層問題的Wilcoxk-ω模型，魯棒性好。此外，與過分耗費(fèi)計(jì)算資源的非定常求解方法相比較，MRF 準(zhǔn)定常求解方法能夠在更加節(jié)省計(jì)算資源的同時(shí)獲得較高的數(shù)值模擬精度，在定軸旋轉(zhuǎn)體氣動(dòng)計(jì)算中應(yīng)用較為廣泛。

2.2 計(jì)算模型

圖4～圖6 所示為研究所采用的幾種計(jì)算模型。為了表述動(dòng)力翼氣動(dòng)特性隨翼面形狀的變化規(guī)律，在圖1 所示研究對(duì)象的基礎(chǔ)上僅改變涵道外壁面翼型輪廓，共建立具有3 種不同彎度的翼型、單元翼段、整體機(jī)翼進(jìn)行對(duì)比。為避免大彎度翼型與涵道內(nèi)壁相結(jié)合會(huì)造成上翼面過厚、下翼面過薄的情況，僅針對(duì)上、下表面均外凸的小彎度翼型進(jìn)行模擬分析，如圖4～圖6 中各計(jì)算模型命名所示：“base”表示相對(duì)彎度為0 的基準(zhǔn)對(duì)稱翼面，“pc01”表示厚度分布不變、最大相對(duì)彎度增大為2.0%的正彎度翼面，“pc02”表示厚度分布不變、最大相對(duì)彎度增大為4.0%的正彎度翼面；“2D”表示二維，“3D”表示三維；“duct-”表示動(dòng)力翼，“-foil”表示剖面翼型，“-wingsec”表示動(dòng)力翼或機(jī)翼的單元翼段，“-wing”表示分布式動(dòng)力翼或機(jī)翼的整體模型。

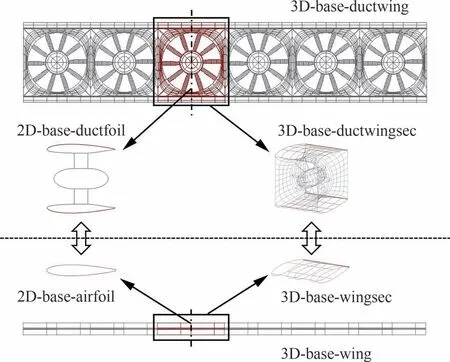
圖4 分布式動(dòng)力翼及常規(guī)機(jī)翼base 模型Fig.4 Distributed-propulsion-wing and traditional wing base model

圖5 分布式動(dòng)力翼及常規(guī)機(jī)翼pc01 模型Fig.5 Distributed-propulsion-wing and traditional wing pc01 model

圖6 分布式動(dòng)力翼及常規(guī)機(jī)翼pc02 模型Fig.6 Distributed-propulsion-wing and traditional wing pc02 model

各計(jì)算模型控制參數(shù)取值如表2 所示，其中base 模 型 給 出 所 有 參 數(shù) 值，pc01 模 型 和pc02 模 型僅給出相對(duì)base 模型發(fā)生改變的參數(shù)值。

表2 各計(jì)算模型控制參數(shù)取值Table 2 Control variables and their values of each model

2.3 網(wǎng)格無(wú)關(guān)性分析

由于所研究的動(dòng)力翼對(duì)象十分復(fù)雜，在進(jìn)行網(wǎng)格劃分時(shí)就需要考慮數(shù)值計(jì)算的效率與精度。因此，以動(dòng)力翼單元翼段base 模型為對(duì)象，建立3 套稀疏程度不同的計(jì)算網(wǎng)格模型，開展網(wǎng)格無(wú)關(guān)性分析。其中，對(duì)涵道筒包裹的圓柱形轉(zhuǎn)動(dòng)區(qū)域（圖4～圖6 中紅色部分區(qū)域）進(jìn)行非結(jié)構(gòu)網(wǎng)格劃分，圓柱體前后面為交界面，圓柱體周向面即為涵道內(nèi)壁。其次，對(duì)動(dòng)力翼單元翼段模型復(fù)雜幾何進(jìn)行邊界層混合網(wǎng)格生成，在黏性壁面附近布置多層半結(jié)構(gòu)化的三棱柱網(wǎng)格作為邊界層網(wǎng)格，在遠(yuǎn)離壁面的區(qū)域布置非結(jié)構(gòu)化四面體網(wǎng)格，同時(shí)在動(dòng)力翼前后緣處進(jìn)行局部網(wǎng)格加密。此外，將動(dòng)力翼單元翼段兩側(cè)平面設(shè)置為對(duì)稱面以忽略翼尖渦三維效應(yīng)，突顯單元特性。

3 套計(jì)算網(wǎng)格基本信息如表3 所示，其主要差異體現(xiàn)在第1 層邊界層網(wǎng)格高度y+、動(dòng)力翼前后緣加密網(wǎng)格尺度、動(dòng)力翼表面網(wǎng)格尺度以及轉(zhuǎn)動(dòng)部件表面網(wǎng)格尺度設(shè)置的不同。

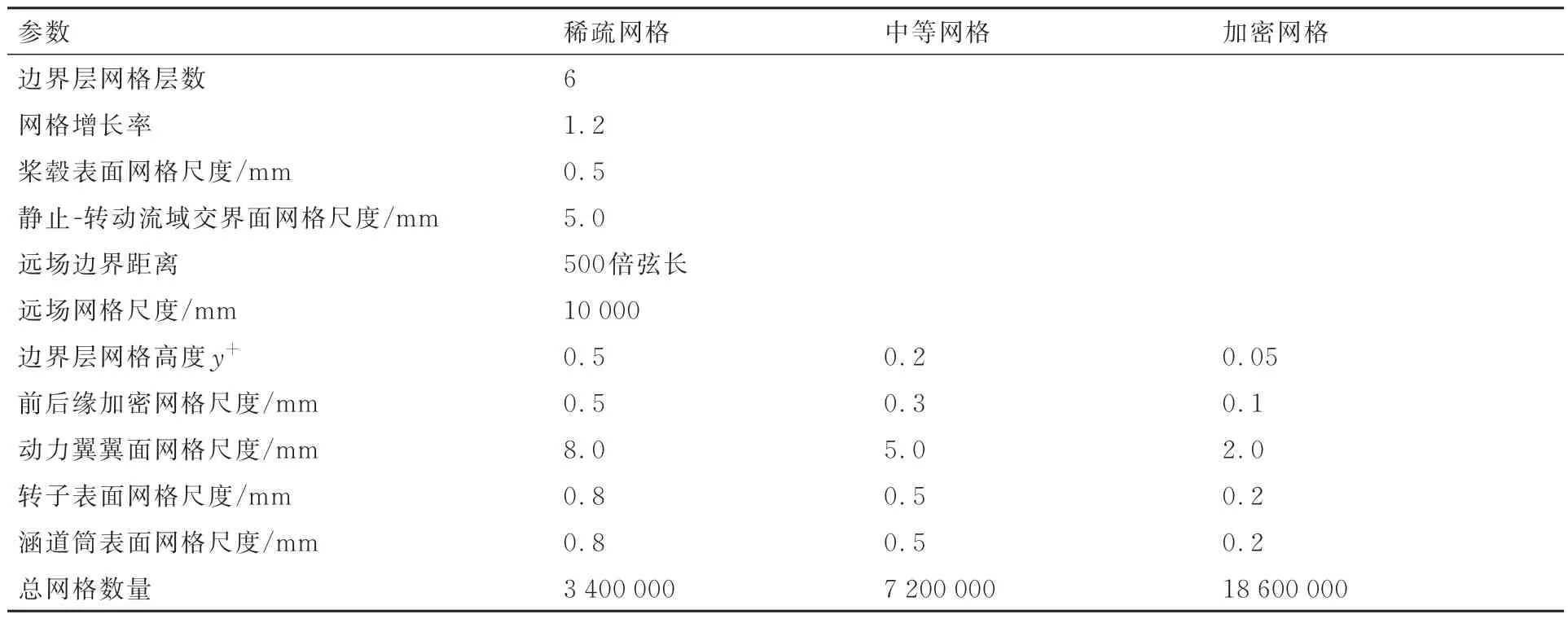
表3 計(jì)算網(wǎng)格信息Table 3 Computational mesh information

選取典型工況進(jìn)行驗(yàn)算，具體計(jì)算狀態(tài)取海拔高度H=0 m、來(lái)流速度V∞=40 m/s、參考面積Sref=0.034 m2、參考展長(zhǎng)bref=0.17 m、 參考弦長(zhǎng)cref=0.2 m、轉(zhuǎn)子速度n=10 000 r/min、迎角α=0°。表4 給出采用3 套網(wǎng)格計(jì)算得到的氣動(dòng)、動(dòng)力特性參數(shù)及求解收斂需用時(shí)間，所有計(jì)算均在同一臺(tái)16 核32 線程64 G 內(nèi)存服務(wù)器中進(jìn)行。可以看出，以加密網(wǎng)格計(jì)算結(jié)果為基準(zhǔn)，中等網(wǎng)格計(jì)算誤差很小，始終在2.20%以內(nèi)，而計(jì)算耗時(shí)顯著縮短，計(jì)算效率顯著提高；稀疏網(wǎng)格對(duì)于轉(zhuǎn)子拉力、轉(zhuǎn)子扭矩以及動(dòng)力翼升力的計(jì)算誤差相對(duì)較小，始終在6.0%以內(nèi)，但對(duì)于動(dòng)力翼阻力計(jì)算誤差十分顯著，達(dá)到23.07%，這與其邊界層網(wǎng)格高度和動(dòng)力翼前后緣加密網(wǎng)格尺度均較大直接關(guān)聯(lián)，而在計(jì)算耗時(shí)上相比中等網(wǎng)格并未體現(xiàn)出明顯優(yōu)勢(shì)。因此在后續(xù)研究中將主要采用中等網(wǎng)格設(shè)置參數(shù)，進(jìn)行動(dòng)力翼特性數(shù)值模擬。

表4 不同計(jì)算網(wǎng)格計(jì)算結(jié)果及耗時(shí)對(duì)比Table 4 Comparison of simulation results and comput?ing time using different computational meshes

3 分布式動(dòng)力翼動(dòng)力/氣動(dòng)耦合特性

借鑒翼型-機(jī)翼研究思路，由動(dòng)力翼二維剖面翼型到動(dòng)力翼單元翼段，再到分布式動(dòng)力翼整體進(jìn)行數(shù)值模擬及詳細(xì)分析，通過將其二維-單元-整體特性內(nèi)在聯(lián)系與常規(guī)翼型-機(jī)翼進(jìn)行比對(duì)，增強(qiáng)對(duì)分布式動(dòng)力翼動(dòng)力/氣動(dòng)耦合特性的認(rèn)識(shí)和理解。

同上進(jìn)行500次仿真實(shí)驗(yàn)，分析各層內(nèi)部節(jié)點(diǎn)剩余能量標(biāo)準(zhǔn)差情況，如圖6所示.可以發(fā)現(xiàn)，由于越靠近基站的節(jié)點(diǎn)累積工作負(fù)荷較大，經(jīng)過能量捕獲后其總體剩余能量的差異度也相對(duì)明顯，故里層的節(jié)點(diǎn)剩余能量相對(duì)不平衡些，總體上變化趨勢(shì)較為平緩，而小車在同一層各停留點(diǎn)的充電時(shí)間相同，從而證明了分層中繼的均衡式路由策略的穩(wěn)定性.

3.1 動(dòng)力翼二維剖面翼型特性

針對(duì)常規(guī)翼型和動(dòng)力翼剖面翼型的二維氣動(dòng)特性進(jìn)行數(shù)值模擬和對(duì)比分析。圖7給出基準(zhǔn)翼型的計(jì)算網(wǎng)格示意，其中，將第1 層邊界層網(wǎng)格高度y+取為0.2，調(diào)整前后緣網(wǎng)格高度不大于0.3 mm、翼型表面網(wǎng)格高度不大于5.0 mm。為了模擬動(dòng)力轉(zhuǎn)子拉力，在動(dòng)力翼剖面翼型流場(chǎng)“Fluid”中設(shè)置轉(zhuǎn)子流域“Rotor-Fluid”，并基于轉(zhuǎn)子拉力設(shè)置空間均布的動(dòng)量源項(xiàng)進(jìn)行數(shù)值模擬，具體計(jì)算狀態(tài)設(shè)置為H=0 m、V∞=40 m/s、cref=0.2 m、轉(zhuǎn)子拉力T=0，7，10，13 N、α=?4°～16°、Δα=4°。此外，在氣動(dòng)特性分析過程中，對(duì)于動(dòng)力翼剖面翼型忽略其槳轂，僅計(jì)入涵道內(nèi)外壁面氣動(dòng)力。

圖7 二維翼型計(jì)算網(wǎng)格Fig.7 Computational mesh around 2D airfoils

圖8 為不同翼型在無(wú)動(dòng)力影響下的升阻力特性曲線，圖中CL為升力系數(shù)，CD為阻力系數(shù)。可以看出，盡管常規(guī)翼型與動(dòng)力翼剖面翼型的升力曲線斜率、零升阻力系數(shù)等差異顯著，但隨著相對(duì)彎度的改變，翼型升阻力變化趨勢(shì)一致，升力曲線斜率、各迎角升力增量、阻力曲線斜率、各迎角阻力增量、大迎角失速特性等均較相近，也就是說(shuō)，在所限定的小彎度翼型情況下，常規(guī)翼型隨彎度變化而產(chǎn)生的氣動(dòng)特性變化規(guī)律在動(dòng)力翼剖面翼型上同樣成立。

圖8 二維翼型氣動(dòng)力特性曲線Fig.8 Aerodynamic force curves of 2D airfoils

圖9 為帶彎度pc02 翼型隨著轉(zhuǎn)子拉力增大后的升阻力特性曲線。可以看出，對(duì)于動(dòng)力翼剖面翼型而言，隨著轉(zhuǎn)子拉力不斷增大，α=0°時(shí)升力系數(shù)基本保持不變，但升力線斜率不斷增大，翼型阻力先增大后減小，翼型升阻比則先減小后增大，且翼型在大迎角狀態(tài)下的失速特性隨著動(dòng)力抽吸效應(yīng)和噴流作用對(duì)流動(dòng)的梳理而稍有改善。

圖9 不同轉(zhuǎn)子拉力下二維pc02 翼型氣動(dòng)力特性曲線Fig.9 Aerodynamic force curves of 2D pc02 airfoils at different thrust levels

圖10 為α=0°，4°時(shí)不同拉力下pc02 翼型壓力分布對(duì)比，圖中Cp為壓力系數(shù)，為便于分析，也給出常規(guī)翼型壓力分布對(duì)比。可以看出：① 在α=0°下，當(dāng)轉(zhuǎn)子拉力為0 N 時(shí)，動(dòng)力翼剖面翼型上、下表面前緣吸力峰值均相比常規(guī)翼型更大；隨著拉力不斷增大，其前緣吸力峰值逐漸減小，壓力分布形態(tài)逐漸趨近于常規(guī)翼型，但受到動(dòng)力內(nèi)流耦合影響，動(dòng)力翼剖面翼型外部流動(dòng)的流速和表面壓力始終相比常規(guī)翼型繞流流速和表面壓力更高和更低。相對(duì)應(yīng)地，動(dòng)力翼剖面翼型上、下表面后緣壓力恢復(fù)值相對(duì)常規(guī)翼型稍小，但隨著轉(zhuǎn)子拉力改變并沒有發(fā)生明顯變化；② 在α=0°迎角下，動(dòng)力翼剖面翼型內(nèi)外流對(duì)應(yīng)的表面壓力分布基本一致。隨著迎角增大，動(dòng)力翼剖面翼型上、下表面前緣吸力峰值均相對(duì)有所增大，動(dòng)力內(nèi)流開始出現(xiàn)軸向不對(duì)稱現(xiàn)象，但各拉力狀態(tài)下轉(zhuǎn)子流域內(nèi)壁的表面壓力值和分布形態(tài)基本一致，這與二維計(jì)算轉(zhuǎn)子拉力直接賦值相關(guān)；③ 在轉(zhuǎn)子拉力為0 N 時(shí)，不同迎角動(dòng)力翼剖面翼型內(nèi)流對(duì)應(yīng)的低壓值均較小，而隨著拉力不斷增大，動(dòng)力翼剖面翼型整個(gè)內(nèi)壁面區(qū)域的低壓值和低壓范圍均不斷增大，此時(shí)動(dòng)力翼剖面翼型上、下表面前緣吸力對(duì)動(dòng)力抽吸帶來(lái)的低壓區(qū)域發(fā)展呈有利誘導(dǎo)；而動(dòng)力翼剖面翼型上、下表面后緣恢復(fù)壓力則對(duì)動(dòng)力噴流低壓區(qū)域發(fā)展有所抑制，這種不對(duì)稱發(fā)展使得在拉力增大到一定程度后，動(dòng)力翼內(nèi)壁面阻力項(xiàng)逐漸轉(zhuǎn)變?yōu)椋ㄘ?fù)阻力）拉力，這也是圖9 中動(dòng)力翼剖面翼型阻力先增大后減小的主要原因。

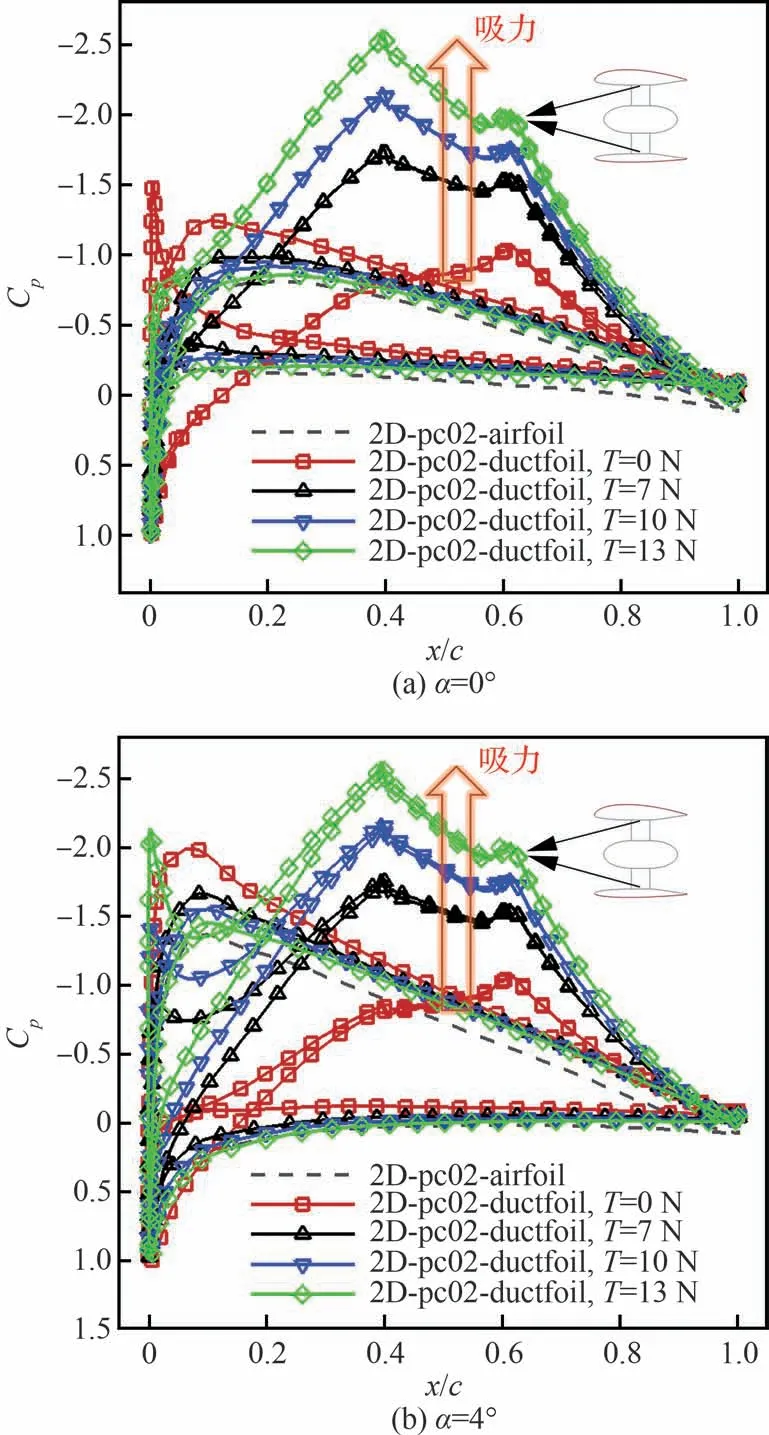
圖10 不同轉(zhuǎn)子拉力下二維pc02 翼型壓力分布對(duì)比Fig.10 Comparison of pressure distributions around 2D pc02 airfoils at different thrust levels

圖11 為迎角α=0°，4°時(shí)動(dòng)力翼不同剖面翼型在相同轉(zhuǎn)子拉力T=10 N 下的壓力分布對(duì)比。可以看出，隨著動(dòng)力翼剖面翼型上下表面輪廓發(fā)生改變，其外部流動(dòng)對(duì)應(yīng)的外壁面壓力分布變化的趨勢(shì)和幅度與常規(guī)翼型壓力分布變化十分相近，而動(dòng)力翼不同剖面翼型內(nèi)流對(duì)應(yīng)的內(nèi)壁面壓力分布始終保持一致。

圖11 相同拉力下不同二維分布式動(dòng)力翼剖面翼型壓力分布對(duì)比Fig.11 Comparison of pressure distributions around dif?ferent 2D distributed-propulsion-wing ductfoils at the same thrust level

3.2 動(dòng)力翼單元翼段特性

進(jìn)一步針對(duì)動(dòng)力翼的單元翼段氣動(dòng)特性進(jìn)行數(shù)值模擬分析。圖12 給出動(dòng)力翼單元翼段的實(shí)體模型多塊網(wǎng)格示意。具體計(jì)算狀態(tài)設(shè)置為H=0 m、V∞=40 m/s、Sref=0.034 m2、bref=0.17 m、cref=0.2 m、n=10 000，11 000，12 000 r/min（對(duì)應(yīng)T=7，10，13 N）、α=?4°～4°、Δα=4°。在氣動(dòng)特性分析過程中對(duì)動(dòng)力翼單元翼段仍忽略其槳轂、轉(zhuǎn)子部件，僅計(jì)入涵道內(nèi)外壁面氣動(dòng)力。

圖13 為轉(zhuǎn)子拉力T=10 N 狀態(tài)各動(dòng)力翼剖面翼型與轉(zhuǎn)子轉(zhuǎn)速n=11 000 r/min 狀態(tài)各動(dòng)力翼單元翼段的氣動(dòng)特性曲線。可以看出：① 由動(dòng)力翼二維剖面翼型到動(dòng)力翼單元翼段，各迎角狀態(tài)下的升力系數(shù)基本一致，這是由于動(dòng)力翼單元翼段實(shí)體具有垂向?qū)ΨQ特征，其涵道內(nèi)壁面壓力上下基本抵消，因此升力特性主要取決于動(dòng)力翼上、下外表面對(duì)應(yīng)的外部流動(dòng)；② 動(dòng)力翼單元翼段阻力相比其二維剖面翼型高出近一倍，這是由于動(dòng)力翼單元翼段相比其二維剖面翼型在流向和展向非對(duì)稱延展，尤其是在不同展向站位上，動(dòng)力翼單元翼段的剖面厚度因圓筒涵道垂向高度減小而顯著增大，其摩擦阻力、壓差阻力均顯著增大，而隨著翼型輪廓變化，動(dòng)力翼單元翼段升阻特性發(fā)展趨勢(shì)與二維計(jì)算結(jié)果基本一致。總的來(lái)說(shuō)，動(dòng)力翼單元翼段氣動(dòng)特性能夠通過其二維剖面翼型進(jìn)行一定程度上的反映，尤其是在升力預(yù)測(cè)方面具備一定的精準(zhǔn)度。

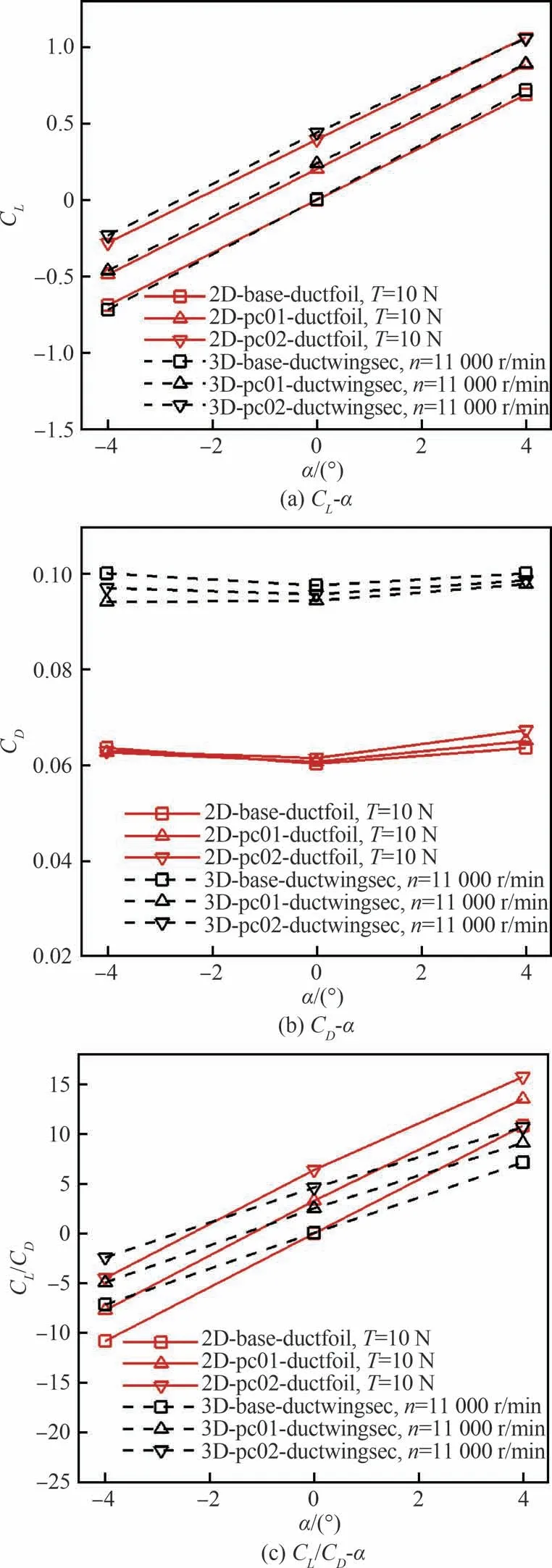
圖13 二維動(dòng)力翼翼型-三維動(dòng)力翼單元翼段氣動(dòng)力特性曲線對(duì)比Fig.13 Comparison of aerodynamic force curves between 2D ductfoils and 3D distributed-propulsion-wing sections

如圖14 所示，截取z=?0.04，0，0.04 m 不同展向站位處的動(dòng)力翼剖面內(nèi)外壁壓力分布進(jìn)行對(duì)比分析。顯然，z=0 m 位置截面翼型與二維剖面翼型一致；而z=±0.04 m 位置截面翼型則由于方轉(zhuǎn)圓進(jìn)氣和圓轉(zhuǎn)方排氣形式與二維剖面翼型輪廓差異顯著，且受轉(zhuǎn)子轉(zhuǎn)動(dòng)方向影響，二者轉(zhuǎn)子流域內(nèi)的葉片截面方向也有所區(qū)別。

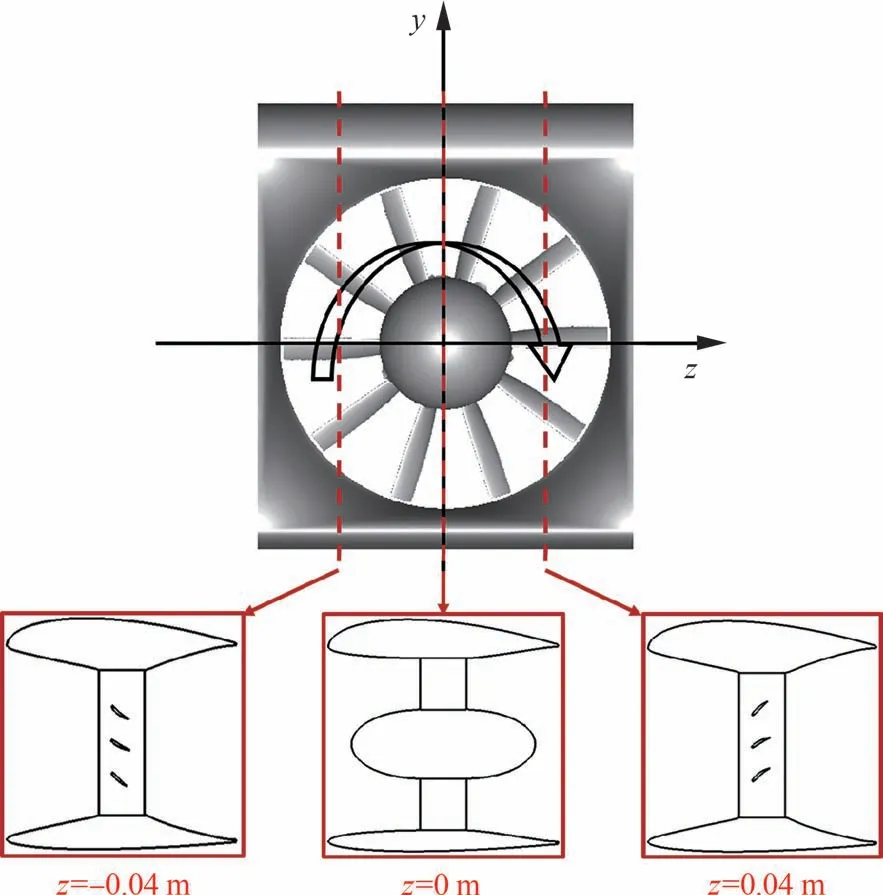
圖14 分布式動(dòng)力翼單元翼段展向截面位置Fig.14 Span-wise locations of distributed-propulsionwing section

圖15 為迎角α=0°、不同轉(zhuǎn)速狀態(tài)pc02 動(dòng)力翼單元翼段z=0 m 截面處翼型壓力分布對(duì)比，為便于分析，圖中也給出動(dòng)力翼二維剖面翼型在不同轉(zhuǎn)子拉力下的壓力分布。可以看出：① 三維動(dòng)力翼單元在轉(zhuǎn)子前后的逆壓梯度相比二維剖面翼型結(jié)果更大，盡管其轉(zhuǎn)子流域內(nèi)低壓峰值及其隨轉(zhuǎn)速（拉力）變化趨勢(shì)與二維剖面翼型結(jié)果基本一致，但其轉(zhuǎn)子流域上、下游受抽吸和噴流影響下的涵道內(nèi)壁壓力值始終相對(duì)二維剖面翼型結(jié)果較高，也就是說(shuō)，二維計(jì)算對(duì)動(dòng)力抽吸效應(yīng)和噴流加速效應(yīng)的預(yù)測(cè)均過于樂觀，這與其所采用動(dòng)量源項(xiàng)設(shè)置對(duì)轉(zhuǎn)子拉力的平均化處理相關(guān)，而相對(duì)地，采用實(shí)體模型旋轉(zhuǎn)設(shè)置的三維計(jì)算對(duì)轉(zhuǎn)子前后的流動(dòng)差異描述更加準(zhǔn)確和真實(shí)；② 涵道三維動(dòng)力翼單元內(nèi)流耦合下的外壁面壓力相比二維剖面翼型始終更低，但其上、下前緣吸力峰值隨轉(zhuǎn)速（拉力）變化趨勢(shì)、變化幅度以及壓力分布輪廓所圍成的面積均與二維剖面翼型結(jié)果較為一致，這也是圖13（a）中升力一致的主要原因。

圖15 不同轉(zhuǎn)速狀態(tài)pc02 分布式動(dòng)力翼單元翼段z=0 m 展向截面翼型壓力分布對(duì)比（α=0°）Fig.15 Comparison of pressure distributions around spanwise section of pc02 distributed-propulsion-wing section at z=0 m among different rotational speed states （α=0°）

圖16 三維pc02 分布式動(dòng)力翼單元翼段不同展向截面翼型壓力分布對(duì)比（n=11 000 r/min， α=0°）Fig.16 Comparison of pressure distributions around 3D pc02 distributed-propulsion-wing section at differ?ent span-wise locations （n=11 000 r/min， α=0°）

圖17 pc02 分布式動(dòng)力翼單元翼段表面壓力及三維流線分布（n=11 000 r/min， α=0°）Fig.17 Surface pressure and 3D streamline distribu?tions around pc02 distributed-propulsion-wing section （n=11 000 r/min， α=0°）

3.3 分布式動(dòng)力翼整體特性

進(jìn)一步針對(duì)分布式動(dòng)力翼整體氣動(dòng)特性進(jìn)行數(shù)值模擬分析。圖18 給出分布式動(dòng)力翼半展長(zhǎng)模型的多塊網(wǎng)格示意，其在轉(zhuǎn)子流域劃分、邊界層網(wǎng)格高度設(shè)置、局部網(wǎng)格加密設(shè)置、氣動(dòng)力計(jì)算設(shè)置等方面均與動(dòng)力翼單元翼段計(jì)算網(wǎng)格保持一致。具體計(jì)算狀態(tài)設(shè)置為H=0 m、V∞=40 m/s、Sref=0.204 m2、bref=1.02 m、cref=0.2 m、n=10 000，11 000，12 000 r/min、α=?4°～4°、Δα=4°。

圖18 三維分布式動(dòng)力翼半展長(zhǎng)模型計(jì)算網(wǎng)格Fig.18 Computational mesh around 3D distributedpropulsion-wing half-span model

考慮到分布式動(dòng)力翼整體可以看作多個(gè)動(dòng)力翼單元翼段沿展向的均勻排布，從動(dòng)力角度出發(fā)，如圖19 所示，以動(dòng)力翼單元翼段的推力、扭矩、推進(jìn)效率為基準(zhǔn)，對(duì)比分析迎角α=0°、轉(zhuǎn)子轉(zhuǎn)速n=11 000 r/min 狀態(tài)下pc02 分布式動(dòng)力翼各單元模塊沿展向的推進(jìn)特性分布曲線。可以看出，分布式動(dòng)力翼相比基準(zhǔn)單元翼段推力特性發(fā)生顯著改變，扭矩分布相對(duì)較大但十分接近，推進(jìn)效率則明顯降低。其中分布式動(dòng)力翼內(nèi)側(cè)單元始終受到相鄰動(dòng)力抽吸誘導(dǎo)，致使其進(jìn)氣流速局部有所增大，動(dòng)力翼推力相比基準(zhǔn)值降低約6.8%，推進(jìn)效率相比基準(zhǔn)值降低約7.7%，而分布式動(dòng)力翼最外側(cè)單元由于受到翼尖渦影響的同時(shí)還需要額外克服最外端表面的摩擦阻力，故其單元推力相比基準(zhǔn)值降低達(dá)22.10%，推進(jìn)效率亦相比基準(zhǔn)值降低約23.10%。

圖19 pc02 分布式動(dòng)力翼展向推進(jìn)特性分布對(duì)比（n=11 000 r/min， α=0°）Fig.19 Comparison of span-wise propulsive properties distributed on pc02 distributed-propulsion-wing（n=11 000 r/min， α=0°）

從機(jī)翼角度出發(fā)，如圖20 所示，以動(dòng)力翼單元翼段的升阻力為基準(zhǔn)，分析迎角α=0°、轉(zhuǎn)子轉(zhuǎn)速n=11 000 r/min 狀態(tài)下pc02 分布式動(dòng)力翼各單元模塊沿展向的升阻特性分布曲線，為便于分析，亦給出相同來(lái)流狀態(tài)下pc02 常規(guī)機(jī)翼的展向升阻特性分布曲線，同時(shí)對(duì)展向分布的升阻力進(jìn)行歸一化處理，圖中L/Lref、D/Dref分別代表構(gòu)型升力、阻力與基準(zhǔn)升力、阻力之比。可以看出，分布式動(dòng)力翼受翼尖渦效應(yīng)影響后的展向升阻力分布變化趨勢(shì)與常規(guī)機(jī)翼基本一致，并未受分布式動(dòng)力內(nèi)流耦合影響而有明顯的改善或惡化。

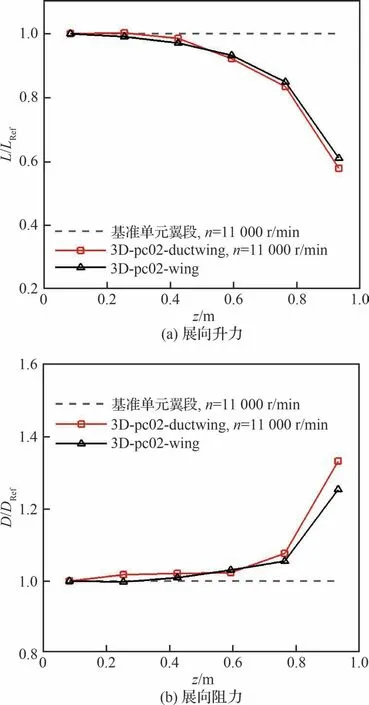
圖20 pc02分布式動(dòng)力翼展向氣動(dòng)力分布對(duì)比（α=0°）Fig.20 Comparison of span-wise aerodynamic force distributed on pc02 distributed-propulsion-wing（α=0°）

圖21 和圖22 分別為與迎角α=0°、轉(zhuǎn)子轉(zhuǎn)速n=11 000 r/min 狀態(tài)下pc02 常規(guī)機(jī)翼和pc02 分布式動(dòng)力翼表面壓力分布和三維空間流線分布示意，其中顯示三維空間流線分布的區(qū)域保持一致。可以看出，分布式動(dòng)力翼上下游空間流線分布特征與圖17 中動(dòng)力翼單元翼段相似，而值得注意的是，分布式動(dòng)力翼尾跡并未出現(xiàn)如常規(guī)機(jī)翼一般明顯的下洗現(xiàn)象，這主要取決于分布式動(dòng)力噴流影響。

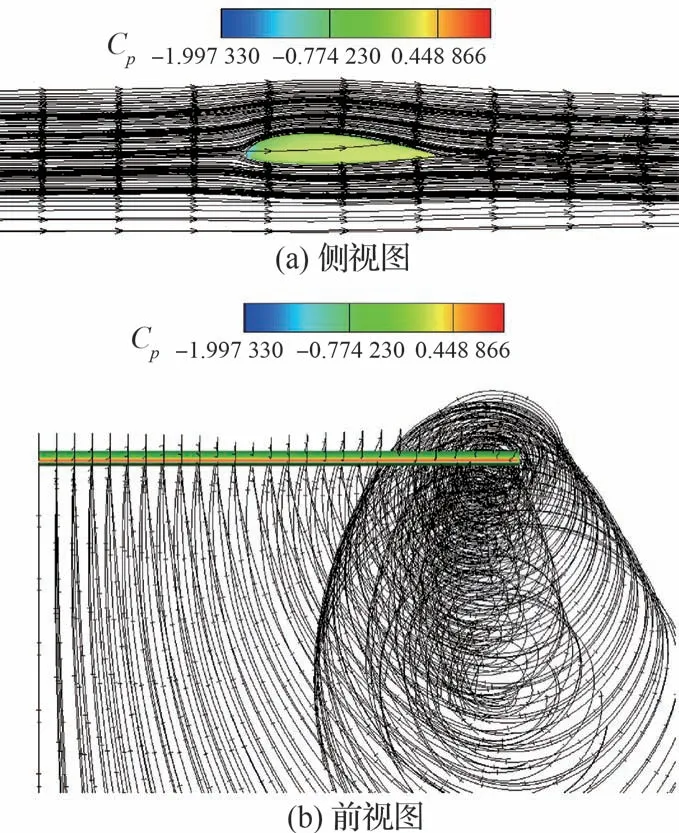
圖21 pc02 常規(guī)機(jī)翼表面壓力及三維流線分布（n=11 000 r/min， α=0°）Fig.21 Surface pressure and 3D streamline distributions around pc02 traditional wing （n=11 000 r/min，α=0°）

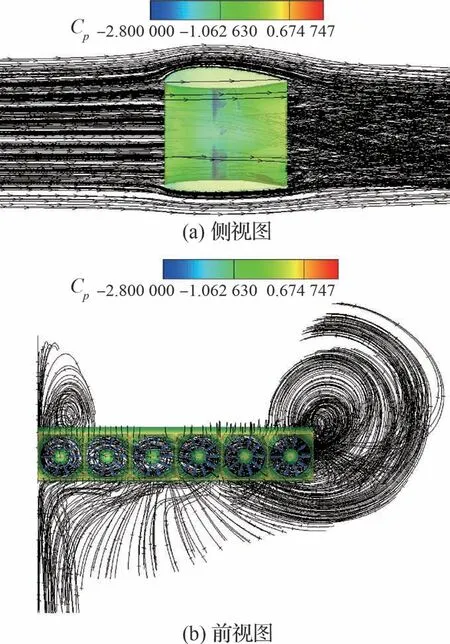
圖22 pc02 分布式動(dòng)力翼表面壓力及三維流線分布（n=11 000 r/min， α=0°）Fig.22 Surface pressure and 3D streamline distribu?tions around pc02 distributed-propulsion-wing（n=11 000 r/min， α=0°）

進(jìn)一步截取pc02 分布式動(dòng)力翼各單元中心截面翼型壓力分布進(jìn)行對(duì)比分析，結(jié)果如圖23 所示，其中z坐標(biāo)值由小到大表示分布式動(dòng)力翼單元由內(nèi)側(cè)向外側(cè)，為便于分析，亦給出動(dòng)力翼單元翼段中心截面的翼型壓力分布。可以看出，分布式動(dòng)力翼各單元?jiǎng)恿?nèi)流對(duì)應(yīng)的涵道內(nèi)壁面壓力分布基本一致，且與動(dòng)力翼單元翼段相應(yīng)的壓力分布吻合良好，但分布式動(dòng)力翼各單元外部流動(dòng)存在明顯差異，表現(xiàn)為上翼面前緣吸力峰值由內(nèi)側(cè)到外側(cè)小幅度減小，直至最外側(cè)單元顯著減小，而下翼面壓力值則由內(nèi)側(cè)到外側(cè)逐漸增大。

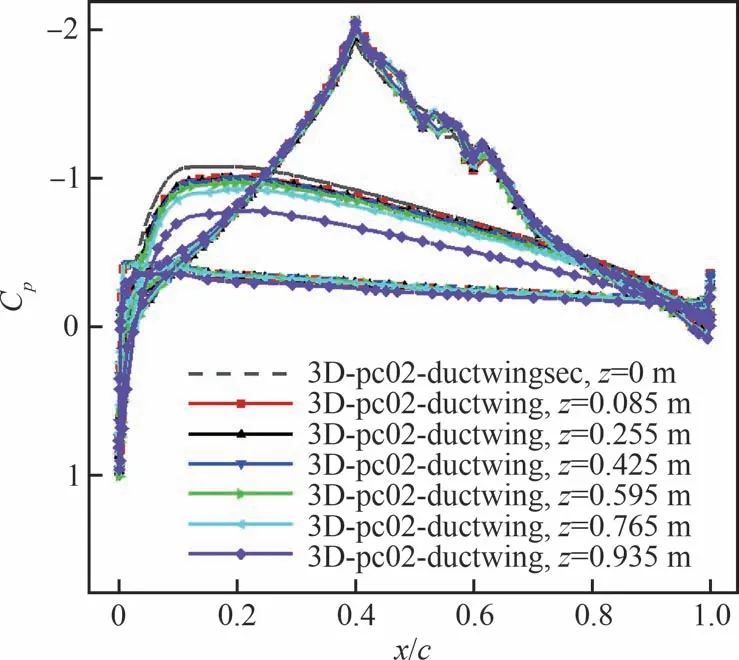
圖23 pc02 分布式動(dòng)力翼各單元中心截面翼型壓力分布對(duì)比（n=11 000 r/min， α=0°）Fig.23 Comparison of pressure distributions around pc02 distributed-propulsion-wing at center sections of each rotor （n=11 000 r/min， α=0°）

4 分布式動(dòng)力翼復(fù)雜對(duì)象設(shè)計(jì)思路

1） 從設(shè)計(jì)角度來(lái)看，分布式動(dòng)力翼具有較為顯著的單元特性，其整體與單元之間關(guān)系與常規(guī)機(jī)翼-翼型較為類似，尤其是在受翼尖渦影響時(shí)，沿展向分布各單元翼段升力變化趨勢(shì)與幅度均與常規(guī)機(jī)翼-翼型基本一致，這無(wú)疑對(duì)于分布式動(dòng)力翼復(fù)雜對(duì)象的氣動(dòng)外形設(shè)計(jì)是有利的，可以等效為忽略翼尖渦效應(yīng)的動(dòng)力翼單元設(shè)計(jì)問題。此外，受動(dòng)力噴流影響，尾流下洗效應(yīng)變?nèi)酰@在采用鴨式布局或串列翼布局的飛行器設(shè)計(jì)過程中需要著重考慮。

2） 從動(dòng)力/氣動(dòng)耦合來(lái)看，分布式動(dòng)力翼內(nèi)外流之間相互影響主要體現(xiàn)在動(dòng)力轉(zhuǎn)子工作狀態(tài)下形成的內(nèi)流低壓區(qū)域與動(dòng)力翼外翼面壓力分布之間的相互作用，其中外翼面前緣吸力對(duì)動(dòng)力轉(zhuǎn)子抽吸下的低壓區(qū)域發(fā)展起到有利誘導(dǎo)作用，而后緣壓力恢復(fù)對(duì)動(dòng)力噴流下的低壓區(qū)域發(fā)展起到抑制作用。此外，相鄰動(dòng)力之間也存在一定的誘導(dǎo)作用，主要影響各動(dòng)力單元進(jìn)氣條件，包括局部流速、局部迎角等，這會(huì)導(dǎo)致分布式動(dòng)力翼各單元的推力和推進(jìn)效率相比獨(dú)立動(dòng)力單元均稍有降低。總的來(lái)說(shuō)，分布式動(dòng)力翼升阻特性與外翼面輪廓、動(dòng)力拉力、內(nèi)外流耦合等密切關(guān)聯(lián)，而以本文動(dòng)力翼內(nèi)壁面進(jìn)行對(duì)稱簡(jiǎn)化處理的研究對(duì)象為例，其升力特性主要取決于外翼面翼型輪廓，阻力特性則主要取決于內(nèi)壁面輪廓、動(dòng)力拉力以及內(nèi)外流耦合強(qiáng)度，尤其在大拉力內(nèi)外流耦合強(qiáng)的狀態(tài)下，動(dòng)力翼阻力特性會(huì)發(fā)生本質(zhì)改變。

基于上述理解，借鑒傳統(tǒng)飛行器拆分解耦設(shè)計(jì)思路，提出如圖24 所示的分布式動(dòng)力翼動(dòng)力/氣動(dòng)一體化設(shè)計(jì)思路：① 基于分布式動(dòng)力翼顯著的單元特性，將其動(dòng)力/氣動(dòng)耦合下的升推一體設(shè)計(jì)問題等效為動(dòng)力翼單元翼段升推一體設(shè)計(jì)問題；② 根據(jù)動(dòng)力內(nèi)外流與升力、推進(jìn)（阻力）特性之間關(guān)系，取動(dòng)力翼剖面翼型進(jìn)行升力特性調(diào)控，取“方-圓”進(jìn)氣道和“圓-方”排氣道進(jìn)行推進(jìn)（阻力）特性調(diào)控，二者之間相互耦合但又相對(duì)獨(dú)立；③ 考慮動(dòng)力翼剖面翼型氣動(dòng)變化規(guī)律與常規(guī)翼型相近，故將其設(shè)計(jì)問題簡(jiǎn)化為常規(guī)翼型的二維曲線設(shè)計(jì)問題，考慮“方-圓”進(jìn)氣道和“圓-方”排氣道在參數(shù)化建模方面均主要依靠進(jìn)口高度、出口高度和3 條控制曲線對(duì)進(jìn)氣段收縮率、排氣段擴(kuò)張率以及進(jìn)排氣段曲面進(jìn)行調(diào)控，故將進(jìn)氣道各控制曲線末端與對(duì)應(yīng)的排氣道控制曲線初端采用直線段連接，進(jìn)而將三維曲面設(shè)計(jì)問題拆解為存在一定內(nèi)在關(guān)系的3 條控制曲線的二維設(shè)計(jì)問題。

圖24 分布式動(dòng)力翼設(shè)計(jì)思路Fig.24 Distributed-propulsion-wing design thread

采用上述思路即可將分布式動(dòng)力翼這一復(fù)雜對(duì)象的動(dòng)力/氣動(dòng)耦合設(shè)計(jì)問題拆解為一個(gè)常規(guī)二維翼型設(shè)計(jì)問題和一個(gè)包含3 條控制曲線多任務(wù)并行的設(shè)計(jì)問題，將特殊問題趨于常規(guī)，進(jìn)而達(dá)到顯著提高設(shè)計(jì)效率、確保工程可實(shí)現(xiàn)的目的。然而，該設(shè)計(jì)思路的缺點(diǎn)在于設(shè)計(jì)過程存在過多的等效和簡(jiǎn)化處理，因此其有效性和可行性將主要取決于設(shè)計(jì)人員先驗(yàn)知識(shí)的準(zhǔn)確性，而且在迭代設(shè)計(jì)過程中將很大程度上依賴于人工干預(yù)，需要在后續(xù)研究工作中增加反向驗(yàn)證和對(duì)比分析。

5 結(jié) 論

針對(duì)分布式動(dòng)力翼動(dòng)力/氣動(dòng)耦合問題，以進(jìn)氣道、排氣道、外翼面等部件分解的方式建立了分布式動(dòng)力翼復(fù)雜對(duì)象的參數(shù)化模型，采用耦合k-ωSST 湍流模型求解RANS 方程的MRF 方法，借鑒常規(guī)翼型-機(jī)翼思路，由動(dòng)力翼二維剖面翼型到動(dòng)力翼單元翼段，再到分布式動(dòng)力翼整體，進(jìn)行了動(dòng)力/氣動(dòng)耦合下的升力、阻力及推進(jìn)特性分析，通過對(duì)小彎度分布式動(dòng)力翼模型的對(duì)比研究，形成結(jié)論如下：

1） 分布式動(dòng)力翼具有較為顯著的單元特性，其整體與單元之間關(guān)系與常規(guī)機(jī)翼-翼型較為類似，尤其是在受翼尖渦影響時(shí)，沿展向分布各單元翼段升力變化趨勢(shì)與幅度均與常規(guī)機(jī)翼-翼型基本一致。此外，分布式動(dòng)力翼升力特性主要取決于動(dòng)力翼單元翼段上、下表面對(duì)應(yīng)的外部流動(dòng)形態(tài)，推進(jìn)（阻力）特性則取決于進(jìn)排氣道、涵道內(nèi)壁對(duì)應(yīng)的動(dòng)力內(nèi)部流動(dòng)形態(tài)以及內(nèi)外流耦合強(qiáng)度。

2） 升力特性方面，由于本文動(dòng)力翼內(nèi)壁面進(jìn)行對(duì)稱簡(jiǎn)化處理，在不同來(lái)流和迎角狀態(tài)下動(dòng)力翼內(nèi)壁壓力在一定程度上始終上下相抵，這使得動(dòng)力翼單元翼段的升力特性曲線與動(dòng)力翼二維剖面翼型升力曲線始終吻合良好。其次，對(duì)于動(dòng)力翼單元翼段的中心截面翼型而言，隨著轉(zhuǎn)子拉力增大，動(dòng)力內(nèi)外流耦合效應(yīng)增強(qiáng)，其上、下前緣吸力峰值會(huì)明顯減小，而后緣恢復(fù)壓力則會(huì)稍有降低，而與二維剖面翼型相比較，其上、下前緣吸力峰值隨轉(zhuǎn)速（拉力）變化趨勢(shì)、變化幅度以及壓力分布輪廓特征等均較為一致。此外，對(duì)于非中心截面翼型而言，其受轉(zhuǎn)子旋轉(zhuǎn)影響帶來(lái)的上下洗特征并不明顯，翼段左右截面壓力分布近似對(duì)稱。

3） 在推進(jìn)（阻力）特性方面，動(dòng)力翼單元翼段不同展向站位截面翼型內(nèi)部流動(dòng)對(duì)應(yīng)的壓力分布差異顯著，這主要是因?yàn)槭艿健胺?圓”進(jìn)氣道和“圓-方”排氣道曲面造型影響，不同展向站位截面翼型內(nèi)壁面輪廓的進(jìn)氣收縮與排氣擴(kuò)張均相比中心截面翼型發(fā)生改變，且在轉(zhuǎn)子流域邊界位置存在明顯的拐點(diǎn)，致使對(duì)應(yīng)區(qū)域壁面壓力存在尖峰。顯然，“方-圓”進(jìn)氣道和“圓-方”排氣道的控制曲線是決定動(dòng)力翼單元翼段推進(jìn)（阻力）特性的關(guān)鍵。此外，動(dòng)力拉力變化會(huì)直接影響動(dòng)力翼內(nèi)壁面區(qū)域的低壓值和低壓范圍，且動(dòng)力翼外流前緣吸力對(duì)動(dòng)力內(nèi)流低壓區(qū)域發(fā)展呈有利誘導(dǎo)，而動(dòng)力翼外流后緣壓力恢復(fù)則對(duì)動(dòng)力內(nèi)流低壓區(qū)域發(fā)展有所抑制，這種弦向不對(duì)稱發(fā)展使得在拉力增大到一定程度后，動(dòng)力翼內(nèi)壁面阻力項(xiàng)將逐漸轉(zhuǎn)變?yōu)椋ㄘ?fù)阻力）拉力，對(duì)應(yīng)動(dòng)力翼阻力特性將發(fā)生本質(zhì)改變。

4） 基于對(duì)小彎度翼型情況下的分布式動(dòng)力翼動(dòng)力/氣動(dòng)耦合特性的理解和認(rèn)識(shí)，借鑒傳統(tǒng)飛行器拆分解耦設(shè)計(jì)思路，提出“利用分布式動(dòng)力翼顯著的單元特性將復(fù)雜對(duì)象等效為動(dòng)力翼單元翼段，同時(shí)將動(dòng)力翼外流與升力特性對(duì)應(yīng)、內(nèi)流與阻力（推進(jìn)）特性對(duì)應(yīng)，相對(duì)獨(dú)立地進(jìn)行調(diào)控，最終將復(fù)雜三維曲面設(shè)計(jì)拆解為常規(guī)翼型輪廓設(shè)計(jì)和存在一定內(nèi)在關(guān)系的多條控制曲線的二維設(shè)計(jì)問題予以解決”的設(shè)計(jì)思路。后續(xù)將進(jìn)一步對(duì)大彎度翼型情況下的分布式動(dòng)力翼動(dòng)力/氣動(dòng)耦合特性進(jìn)行深入研究，分析本文相關(guān)理解和認(rèn)識(shí)的普適性，同時(shí)也將結(jié)合具體算例對(duì)采用上述思路開展分布式動(dòng)力翼設(shè)計(jì)的有效性和可行性進(jìn)行驗(yàn)證。