基于全局敏感性的自適應模型更新混合模擬方法

陳再現(xiàn), 王紀偉,2, 鐘煒彭, 劉 鋮, 李明剛

(1.哈爾濱工業(yè)大學(威海) 海洋工程學院, 山東 威海 264209; 2.中建三局第一建設工程有限責任公司,湖北 武漢 430040)

混合模擬把計算機難以精確模擬的復雜非線性部分作為物理子結(jié)構(gòu)進行真實的物理加載,其余部分作為數(shù)值子結(jié)構(gòu)在計算機中建模計算,在20世紀70年代初由日本學者Hakuno等[1]提出,并在20世紀70年代中期由日本學者Takanashi等[2]第一次實現(xiàn)。混合模擬減少了試驗成本和試驗場地及設備的要求,并且也較為真實地反映了非線性較強構(gòu)件的受力情況。因此被普遍認為是一種經(jīng)濟高效且極具有發(fā)展前景的新型抗震試驗技術(shù)。

數(shù)值子結(jié)構(gòu)的精確程度是影響混合模擬結(jié)果的重要因素。模型更新依據(jù)試驗子結(jié)構(gòu)反饋數(shù)據(jù)不斷修正數(shù)值子結(jié)構(gòu),因此能較好地提升數(shù)值子結(jié)構(gòu)的模型精度。近年來,模型更新備受眾多學者關注。Yang等[3]首次將模型更新引入到混合模擬,利用神經(jīng)網(wǎng)絡對數(shù)值結(jié)構(gòu)建模,通過試驗子結(jié)構(gòu)反饋數(shù)據(jù)不斷修正神經(jīng)網(wǎng)絡,并在二層剪切模型中通過數(shù)值模擬和真實試驗進行了驗證。Elanwar等[4-5]以數(shù)值子結(jié)構(gòu)和物理子結(jié)構(gòu)的應力差值作為目標函數(shù),對材料本構(gòu)參數(shù)進行識別,數(shù)值模擬結(jié)果表明,基于材料本構(gòu)模型參數(shù)的更新方法能提高混合模擬的精度。Yang等[6-7]分別開展了鋼框架和鋼筋混凝土橋墩的混合模擬工作,從材料本構(gòu)模型層面對參數(shù)進行更新并驗證了其對混合模擬精度的提升。Zhong等[8]提出采用均勻設計的方法對鋼結(jié)構(gòu)和鋼筋混凝土結(jié)構(gòu)材料參數(shù)進行識別,該方法極大地降低了樣本數(shù)量,提高了識別效率,該方法在二層框架中以數(shù)值模擬的方式得到了驗證。王濤等[9-10]提出統(tǒng)計容積卡爾曼濾波器的模型更新方法,并引入多尺度模型更新概念,通過二層帶有自復位摩擦耗能支撐框架結(jié)構(gòu)的數(shù)值模擬分析驗證了方法的可行性。

模型更新首先依據(jù)尋優(yōu)方法創(chuàng)造樣本空間,然后利用試驗子結(jié)構(gòu)反饋數(shù)據(jù)確定最優(yōu)樣本點,最后更新至數(shù)值結(jié)構(gòu)。從模型更新的過程來看,它是求解逆問題,根據(jù)試驗子結(jié)構(gòu)反饋數(shù)據(jù)識別多參數(shù),樣本空間的選取不當直接影響參數(shù)識別的效果。陳再現(xiàn)等[11-12]提出基于全局敏感性(global sensitivity, GS)的混合模擬試驗方法,通過參數(shù)敏感度系數(shù)確定參數(shù)的搜索范圍即樣本空間能使參數(shù)更容易收斂到有效值。然而,在多參數(shù)識別過程中,僅通過固定的靈敏度系數(shù)去指導模型更新易導致參數(shù)陷入局部最優(yōu),從而降低模型更新的精度。基于此,將動量和自適應步長的概念引入模型更新中,提出基于全局敏感性的自適應(global sensitivity adaptive, GS-A)混合模擬試驗方法在一定程度上彌補了僅用敏感度系數(shù)確定樣本空間的缺陷,提升了參數(shù)收斂的速度和模型更新的精度。下文通過介紹所提出方法的基本原理、用以驗證該方法的數(shù)值模型和更新參數(shù)的選擇以及數(shù)值模擬方案,通過33個數(shù)值模擬算例驗證本文方法的有效性。

1 GS-A混合模擬模型更新方法基本原理及流程

1.1 基本原理

陳再現(xiàn)等推出的GS模型更新混合模擬方法使用均勻設計選擇樣本空間時,以上一步最優(yōu)參數(shù)為搜索中心,各參數(shù)搜索步長與對應的敏感性系數(shù)成正比,利用相應的均勻設計表[13]生成驗算子結(jié)構(gòu)樣本空間。

然而在參數(shù)識別過程中,若固定中心點(上一步最優(yōu)參數(shù)組合),創(chuàng)建樣本空間,對當前步最優(yōu)參數(shù)進行搜索,會出現(xiàn)與參考模型差異較大的參數(shù)不能迅速被識別,設置落入局部最優(yōu)點,因此基于全局敏感性的自適應(GS-A)模型更新混合模擬方法引入動量概念,即參考歷史參數(shù)變化,引導參數(shù)朝著最優(yōu)值更快收斂,動量表達式為

(1)

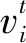
在參數(shù)識別的最初階段,參數(shù)組合距離目標函數(shù)的最優(yōu)解距離很遠,但是隨著參數(shù)識別的次數(shù)變大,參數(shù)組合會越來越接近最優(yōu)解,因此本文提出對搜索步長進行自適應處理,依據(jù)每個參數(shù)的變化量大小來調(diào)整各個參數(shù)的步長,使參數(shù)組合在接近最優(yōu)解時,步長將適當縮小,使參數(shù)組合更加趨近于最優(yōu)解。自適應步長計算公式見式(2)～式(3)

(2)

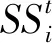
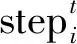
(3)

式中,ε為維持數(shù)值穩(wěn)定性所添加的常數(shù),本文取為10-8。

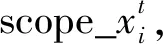
(4)

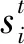
(5)

式中,TSi為t時刻,第i個參數(shù)的總階靈敏度系數(shù)。

1.2 基本流程

數(shù)值模擬所采用的數(shù)值模型[14]由全結(jié)構(gòu)數(shù)值模型、物理子結(jié)構(gòu)和驗算子結(jié)構(gòu)三部分組成,如圖1所示上部三個部分。將地震激勵輸入到全結(jié)構(gòu)數(shù)值模型,通過時程分析獲取當前步的內(nèi)力和位移,并輸入到物理子結(jié)構(gòu)和驗算子結(jié)構(gòu)中,獲得恢復力,不同的是,物理子結(jié)構(gòu)的恢復力為參考目標,驗算子結(jié)構(gòu)是物理子結(jié)構(gòu)的數(shù)值模擬空間(通過優(yōu)化算法選擇),兩者除更新參數(shù)外均相同,依據(jù)目標函數(shù)選取與物理子結(jié)構(gòu)恢復力誤差最小的驗算子結(jié)構(gòu),將其參數(shù)更新到計算全結(jié)構(gòu)中,從而進行下一地震步的計算。如圖1所示模型更新基本流程,具體步驟如下:

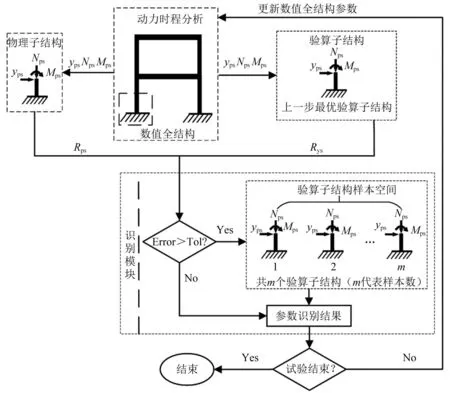
圖1 模型更新流程圖

步驟1利用動力時程分析求出數(shù)值全結(jié)構(gòu)結(jié)構(gòu)響應,提取出子結(jié)構(gòu)劃分界面處的位移及內(nèi)力(界面位移yps,軸力Nps和彎矩Mps),并發(fā)送到物理子結(jié)構(gòu)和驗算子結(jié)構(gòu)。

步驟2物理子結(jié)構(gòu)和驗算子結(jié)構(gòu)接收到位移與內(nèi)力,完成加載后得到各自的恢復力,并根據(jù)誤差判斷規(guī)則,選擇是否啟動更新程序,目標函數(shù)選取與物理子結(jié)構(gòu)恢復力誤差最小的驗算子結(jié)構(gòu),如式(6)所示,如果啟動,進入步驟3,如果不啟動,返回步驟1進行下一步動力時程分析。

步驟3依據(jù)式(4)所確定的參數(shù)搜索范圍,利用均勻設計得到驗算子結(jié)構(gòu)樣本空間,識別程序比較樣本空間中多個驗算子結(jié)構(gòu)與物理子結(jié)構(gòu)恢復力的相對累積誤差,選出誤差最小的驗算子結(jié)構(gòu),將其參數(shù)組合作為更優(yōu)參數(shù)組合發(fā)送到全結(jié)構(gòu)數(shù)值模型進行參數(shù)更新,并進行下一步動力時程分析。

步驟4直到地震動記錄結(jié)束,終止程序,否則,重復步驟1～步驟4。

(6)

式中:Rps(i)為物理子結(jié)構(gòu)恢復力,作為參考值;Rys(i)為驗算子結(jié)構(gòu)恢復力。

2 數(shù)值模擬方案

2.1 基本模型構(gòu)建

選用一榀二層一跨的鋼框架框結(jié)構(gòu),一層和二層高度分別為3 600 mm和3 000 mm,跨度6 000 mm,框架幾何尺寸、質(zhì)量及荷載分布如圖2所示,質(zhì)量及荷載分布參照GB 50011—2010《建筑抗震設計規(guī)范》與GB 50009—2012《建筑結(jié)構(gòu)荷載規(guī)范》計算所得,截面信息分別如圖2和圖3所示。

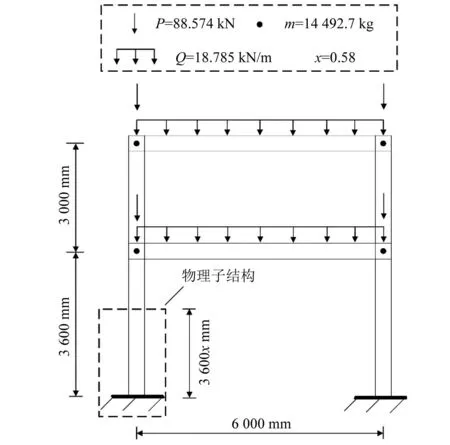
圖2 框架模型

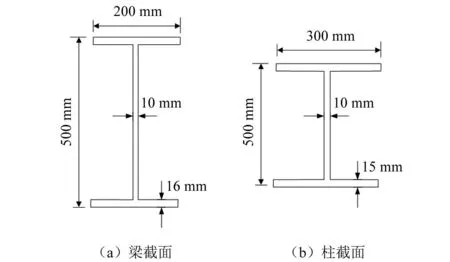
圖3 鋼框架截面

物理子結(jié)構(gòu)與數(shù)值子結(jié)構(gòu)的界面設置在彈性反彎點處[15],由D值法計算得到鋼框架的反彎點分別為底柱長度的0.58倍處,如圖2所示。采用OpenSees有限元軟件進行數(shù)值建模,鋼材本構(gòu)模型采用雙線性模型(Steel01),模型假定基礎與地基剛性連接,框架結(jié)構(gòu)采用基于力的非線性梁柱單元(nonlinear beam-column element),每個單元選取5個Gauss-Lobatto,截面為纖維截面。

2.2 更新參數(shù)確定及模擬方案

選用雙線性鋼材本構(gòu)模型(Steel01),更新參數(shù)為8個:彈性模量Es,屈服強度fys以及硬化系數(shù)bs,尺寸參數(shù)為高度h、寬度d、腹板厚度t1和翼緣厚度t2,以及柱長ls。參數(shù)的參考值設置如表1所示,將各個參數(shù)比例化,設定參數(shù)的參考值為1,模型的材料誤差參數(shù)浮動范圍設為(0.7～1.3),尺寸誤差參數(shù)浮動范圍設為(0.98～1.02)。

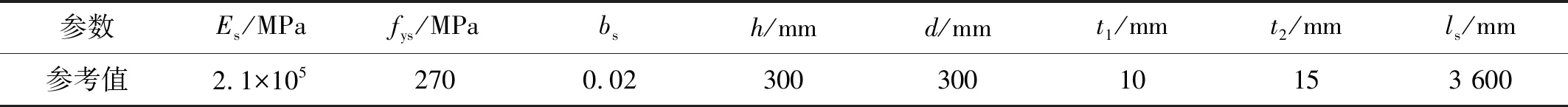
表1 鋼結(jié)構(gòu)參數(shù)參考值

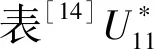
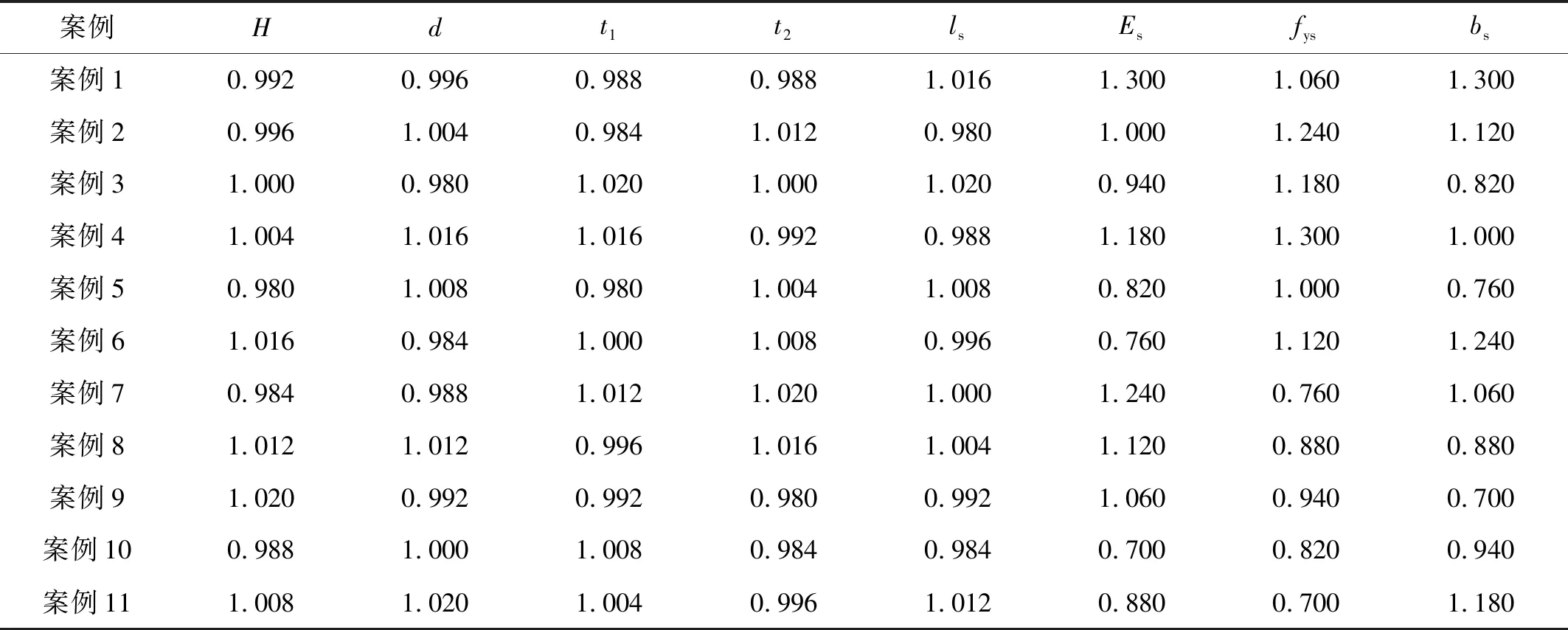
表2 初始參數(shù)組

為驗證GS-A方法模型更新效果,把不更新混合模擬(hybrid simulation,HS)和GS模型更新方法作為對照組。HS用于反映傳統(tǒng)混合模擬中各參數(shù)是帶有誤差的統(tǒng)計值的情況并且在試驗過程中參數(shù)不被更新。GS方法和GS-A方法分別為在混合模擬中采用基于全局敏感性的模型更新方法和基于全局敏感性的自適應模型更新方法,在試驗過程中參數(shù)不斷地被更新。數(shù)值模擬方案如表3所示。

表3 數(shù)值模擬方案

3 數(shù)值模擬結(jié)果

各參數(shù)對一層位移相對累計誤差的敏感性在地震的各個時間段是不斷變化的,因此對試驗模型參數(shù)進行分階段敏感性分析,并以此結(jié)果作為模型更新驗算子結(jié)構(gòu)樣本空間選擇的依據(jù),敏感性分析方法采用Sobol法[16]。設置地震峰值加速度( peak ground acceleration,PGA)為510 gal的El Centro波作為地震激勵,取持續(xù)6 s的地面運動記錄,積分步長取0.01 s。地震分階段靈敏度系數(shù)變化如圖4所示。根據(jù)Sobol分析結(jié)果,在結(jié)構(gòu)處于彈性階段時(2 s之前),參數(shù)彈性模量和翼緣寬度的敏感度系數(shù)最大,在結(jié)構(gòu)經(jīng)歷塑性階段時(2 s之后),參數(shù)屈服強度敏感度系數(shù)開始增大,屈服強度、彈性模量和翼緣厚度的敏感性排名前三。

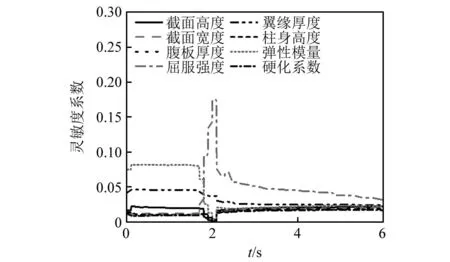
圖4 地震分階段鋼框架模型參數(shù)靈敏度系數(shù)變化圖

參考解(Ref)是模型參數(shù)為參考值時的時程分析結(jié)果。對照組分別為參數(shù)不更新時混合模擬(HS)的結(jié)果和采用基于全局敏感性(GS)的模型更新方法進行模型更新的結(jié)果。采用物理子結(jié)構(gòu)位移相對累積誤差和峰值位移相對誤差作為模擬結(jié)果精度的評價指標,分別如式(7)和式(8)。

(7)

式中:yref(i)為物理子結(jié)構(gòu)位移參考值,由時程分析得出;yps(i)為物理子結(jié)構(gòu)位移。

(8)

式中:y_maxref為物理子結(jié)構(gòu)峰值位移參考值,由時程分析得出;y_maxps為物理子結(jié)構(gòu)峰值位移。

鋼框架模型更新效果如圖5所示,在11個初始誤差參數(shù)組中,相對于HS,使用GS-A方法和GS方法更新完成后模型的物理子結(jié)構(gòu)處位移時程與參考位移時程的相對累積誤差均有所降低,并且,兩種模型更新方法對峰值位移相對誤差均有所改善,但是GS-A更新效果明顯優(yōu)于GS,GS-A物理子結(jié)構(gòu)處位移的相對累積和峰值位移相對誤差均在5.7%和2.7%以內(nèi),而GS在案例7中甚至達到了52.9%和28.4%;11個初始誤差參數(shù)組中,GS-A方法和GS方法的物理子結(jié)構(gòu)處位移的相對累積誤差和峰值位移相對誤差的均值和提升效果如表4所示,GS-A方法物理子結(jié)構(gòu)處位移的相對累積和峰值位移相對誤差的均值為2.3%和1.3%,均優(yōu)于GS方法的17.8%和9.4%,相對于HS,分別提升了97.1%和96.6%,提升效果均優(yōu)于GS方法的78.3%和74.5%。

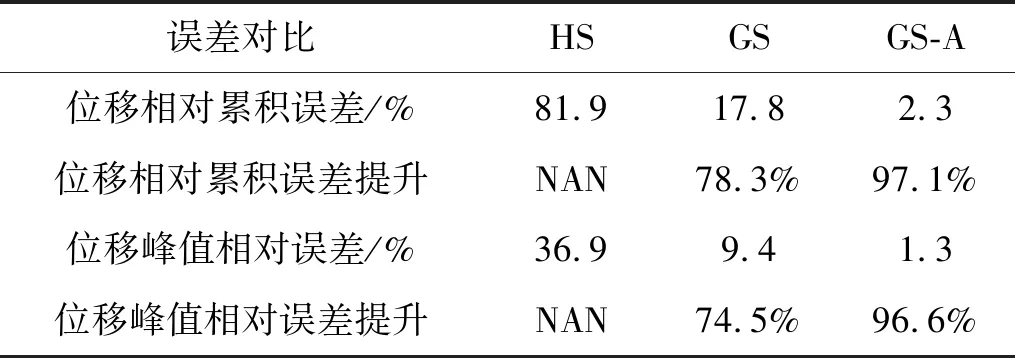
表4 模型更新提升效果

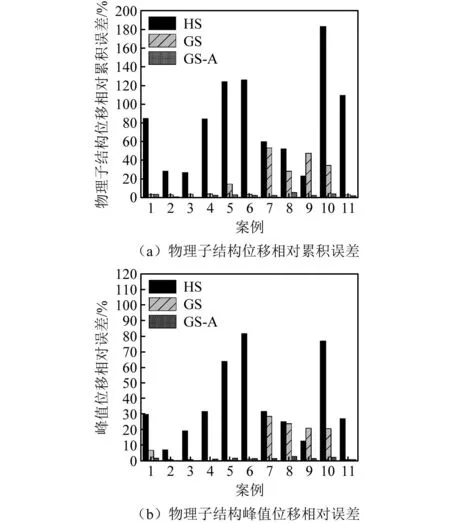
圖5 鋼框架(steel01本構(gòu)模型)更新效果圖

GS方法和GS-A方法對11個初始誤差參數(shù)組的參數(shù)識別結(jié)果的平均誤差如表5所示,表中按參數(shù)敏感性由大到小排序。可見,GS-A方法的參數(shù)識別誤差相對于GS方法有所降低,值得注意的是,對于敏感性最小的硬化系數(shù)bs,GS-A方法能有效識別,且平均誤差僅有1.3%,GS方法則識別失效,平均誤差達到27.9%。

表5 模型更新后參數(shù)平均誤差

GS方法和GS-A方法在模型更新后段(4～6 s)中各參數(shù)的平均相對誤差和標準差如表6所示,表中按參數(shù)敏感性由大到小排序。GS-A方法參數(shù)平均相對誤差均小于2.3%,而GS方法對敏感性較大的參數(shù)彈性模量的識別平均誤差達到4.9%,對于敏感性較小的硬化系數(shù)平均誤差達到27.9%。對于參數(shù)識別過程的標準差,GS-A方法均小于GS方法,因此GS-A方法的穩(wěn)定性明顯優(yōu)于GS方法。

表6 模型更新(4～6 s)參數(shù)平均誤差和標準差

在11個案例中,案例9所對應的GS方法的位移的相對累積誤差和峰值相對誤差均比HS大,以此選取案例9的參數(shù)識別過程、位移時程與滯回曲線對比示例。

案例9的參數(shù)識別過程對比如圖6所示,GS方法和GS-A方法在模型更新后段(4～6 s)中各參數(shù)的標準差如表7所示,GS-A方法的標準差均低于GS方法,因此GS-A方法的參數(shù)識別的穩(wěn)定性優(yōu)于GS方法。值得注意的是,在GS方法中,各參數(shù)在識別過程中不斷上下波動,說明參數(shù)陷入局部最優(yōu)值,從而來回震蕩,反觀GS-A方法,動量使樣本空間中心向參數(shù)變化方向移動,參數(shù)更快地收斂,自適應系數(shù)調(diào)整樣本空間的范圍,防止參數(shù)組合陷入局部最優(yōu)。GS方法和GS-A方法參數(shù)最終識別值與參考值的比值如表8所示。由表8可知,GS-A方法的參數(shù)識別誤差相對于GS方法均有所降低,提升了模型更新精度。

表7 模型更新(4～6 s)參數(shù)標準差(案例9)

表8 參數(shù)最終識別值與參考值比值(案例9)

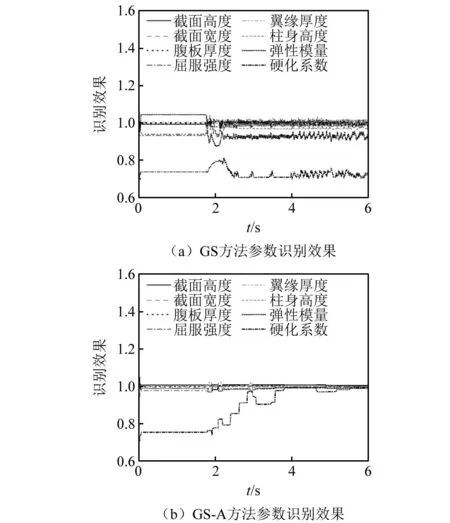
圖6 參數(shù)更新效果圖(案例9)

案例9的物理子結(jié)構(gòu)位移時程和滯回曲線對比見圖7和圖8,GS-A方法的位移時程曲線和滯回曲線相對HS和GS方法更貼近于參考解(Ref)。GS-A方法的物理子結(jié)構(gòu)位移與參考解的相對累積誤差為2.27%,遠小于HS的23.05%和GS方法的47.16%,因此GS-A方法顯著地提升了模型更新效果。

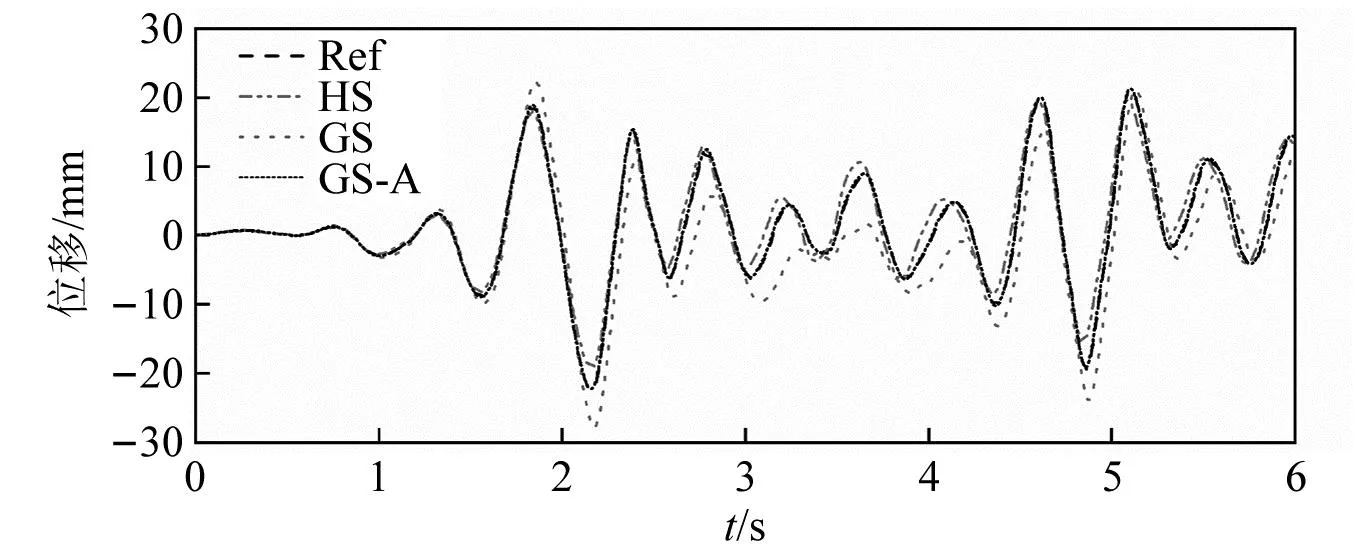
圖7 位移曲線對比圖(案例9)

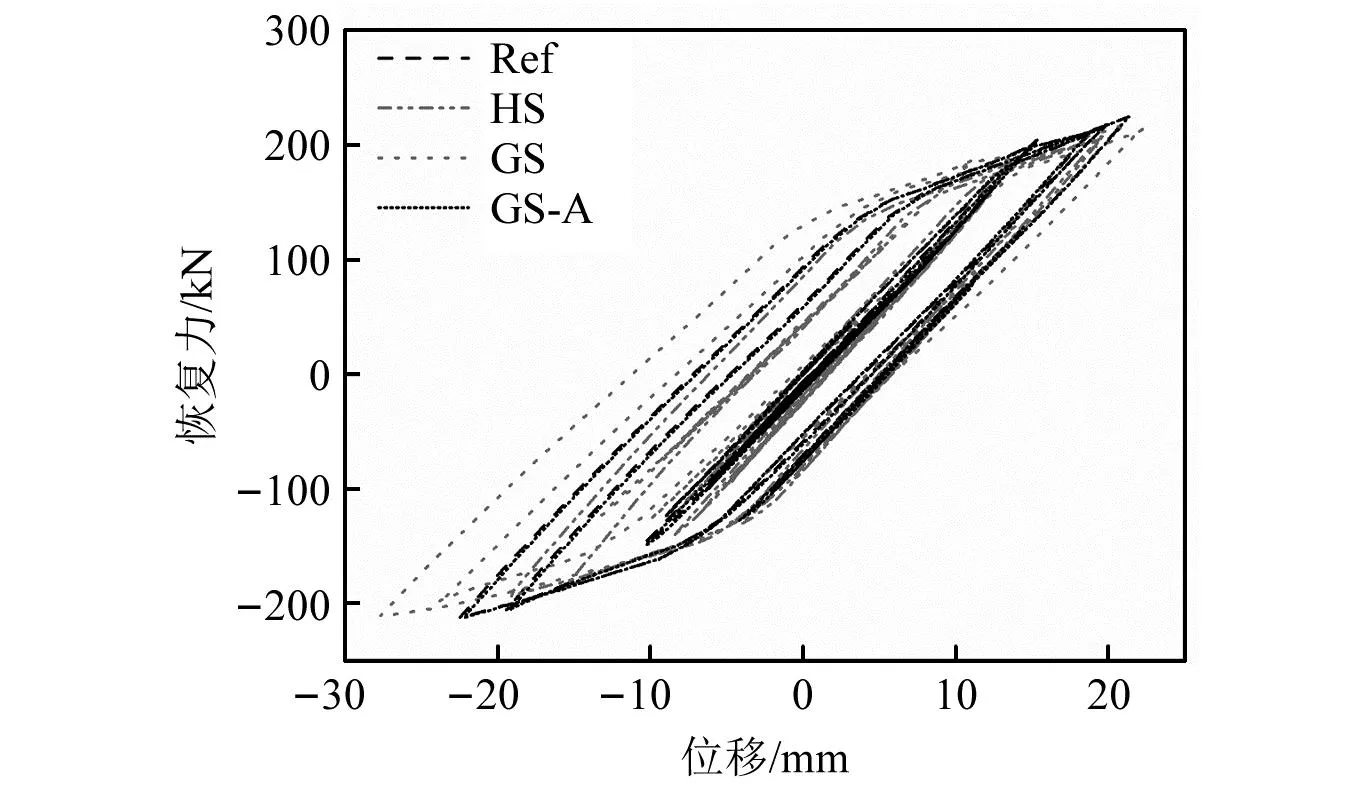
圖8 滯回曲線對比圖(案例9)

4 結(jié) 論

(1)提出了GS-A模型更新混合模擬方法,在鋼框架中進行了11種不同初值參數(shù)誤差組的數(shù)值模擬用以驗證該方法的適用性,驗證了動量和自適應策略的可行性。模擬結(jié)果顯示,GS-A方法的相對累積誤差和物理子結(jié)構(gòu)峰值位移相對誤差的均值分別為2.3%和1.3%,相對于GS方法的17.8%和9.4%有顯著提升,改善了模型更新效果。

(2)在參數(shù)識別精度方面,在GS方法中敏感性較大的參數(shù)彈性模量的平均相對誤差達到了6.0%,敏感性較小的參數(shù)硬化系數(shù)識別效果欠佳,平均相對誤差達到了27.1%,而GS-A方法各參數(shù)的平均相對誤差均在1.4%以內(nèi),GS-A方法相對于GS方法有效地提升了參數(shù)識別的精度。

(3)在參數(shù)識別后段(4～6 s),GS-A方法中的各參數(shù)標準差平均值均小于GS方法,因此GS-A方法提升了參數(shù)識別的穩(wěn)定性。

(4)案例9中,GS方法參數(shù)組合陷入局部最優(yōu)解,因此導致模型更新效果比不更新還差。GS-A方法解決了參數(shù)陷入局部最優(yōu)解的問題,參數(shù)識別效果的精度和穩(wěn)定性均優(yōu)于GS方法,且位移時程和滯回曲線相對于HS和GS方法均更貼近于參考解,物理子結(jié)構(gòu)位移相對累積誤差僅有2.3%,顯著地提升了模型更新效果。