整體觀視角下數學境脈教學模式實踐與探索
——以“用二分法求方程的近似解”為例

張召生 王瑞菲 (郵編:273165)

曲阜師范大學數學科學學院

按照Mario Antonio Kelly博士的定義,境脈是指,“學生和教師組成的一個具體班級中,由包括課堂的物理環境(軟硬件基礎設施)、學生的家庭背景、認知特點、心理素質和班級的精神面貌等諸多因素結合在一起的協同作用”[1].境脈包含學生生理、心理、思維、認知、知識,以及文化、社會等多個方面.境脈教學的本質就是在教學目標的指引下,教師以學生為主體,以素養為導向,設計出一脈相承且交互性強的教學情境.境脈教學的設計帶給學生全身心的參與感和沉浸式的體驗感,促使學生從“獲得知識”轉向“參與知識”.

《普通高中數學課程標準(2017年版2020年修訂)》(以下簡稱《課標》)指出“高中數學教學以發展學生數學學科核心素養為導向,創設合適的教學情境,啟發學生思考,引導學生把握數學內容的本質.”[2]可見,創設好情境是數學教學的關鍵問題之一.情境是多樣的、多層次的,《課標》提出“教學情境包括:現實情境、數學情境、科學情境,每種情境可以分為熟悉的、關聯的、綜合的.”[2]境脈教學符合課標要求,“脈”字體現主體性、系統性、整體性,不僅指內容的整體結構(概念及其相互聯系),以及前后一致的由內容反映的數學思想方法[3],更涵蓋學生在境脈中所構建的認知體系、學生心理和班級風貌特點等.因此,境脈教學符合教學和學生發展的規律,應多加探索和實踐.《課標》要求教師“在教學實踐中,要不斷探索和創新教學方式”“在教學活動中,應勇于創新,包括教學方式的創新,也包括從教學實踐中總結經驗……實現對自身數學教學經驗的不斷反思和超越”[2].教師應在實踐中不斷反思與提升,最終超越原經驗教學.所以教師應積極探索,將學生經驗、心理、知識與環境等因素整體納入教學,搭建教學境脈,形成境脈教學.

整體觀是指從全局考慮問題的觀念,在整體意義上體察事物,所有因素都被納入系統中,相互連接、結合,從而得到更優的結論.在整體觀視角下,設計四條境脈,利用四種線索形成教學境脈,從而得到整體觀視角下數學境脈教學模式.在教學比賽中,作者根據該模式設計“用二分法求方程的近似解”一課,學生反饋良好,取得不錯的教學效果.在此展示教學模式和教學實踐,一起研討交流.

1 整體觀視角下數學境脈教學模式的構建

如何構建境脈教學呢?首先要搭建四條境脈:經驗境脈、心理境脈、知識境脈與環境境脈.教師要關注學生的經驗境脈,即學生整體已有的認知結構與認知特點、數學學科核心素養發展水平、數學學習經驗等;了解學生的心理境脈,即學生心理發展階段特征以及學生對本節課學習的興趣、態度、情緒等;解析課程的知識境脈,即知識本身、知識的發展歷史、知識的實際應用、知識間的結構脈絡、知識背后的思想方法、與其他學科知識間的融合等;熟悉教學的環境境脈,即班風班紀、教室環境、配備的數字化設備、虛擬空間、線上交流平臺等.

構建教學境脈,教師需以整體觀視角,審視、解析并把握教學現實和教學內容,立足于對教學現實和教材內容的全局掌控之上,展望數學核心素養的要求.教學境脈旨在推動有意義學習,幫助學生從四條境脈中獲取所需,經歷知識再創造的過程,促進新知融入已有的認知結構中.

整體觀視角下數學教學境脈的設計,可分為四種線索:情境線索、活動線索、知識線索和素養線索[4].由情境線索引導活動線索,借助活動成果抽象知識線索,這本質上是數學化的過程,以此達到素養線索的目標.同時,四種線索靈活組合且要確保內容不偏離脈絡.再者,境脈設計有三種結構,分別為:串聯型、并聯型和復合型[4],由此保障教師可根據教學要求設計出整體最優化的境脈教學.基于此,得到整體觀視角下數學境脈教學模式,如圖1.

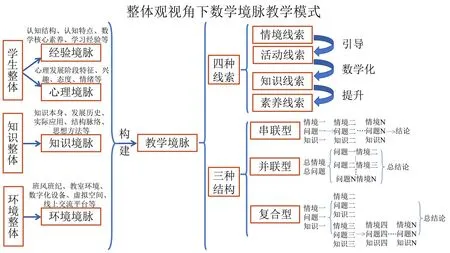
圖1

2 整體觀視角下“用二分法求方程的近似解”境脈教學案例設計和實踐

2.1 整體觀視角下“用二分法求方程的近似解”境脈教學案例設計

以“用二分法求方程的近似解”為例,展示整體觀視角下境脈教學設計和實踐.

(1)整體導向,構建四條境脈

“用二分法求方程的近似解”是人教A版必修一第四章第四節《函數的應用(二)》的第二節課.基于本節內容,設計四條境脈,分析如下(如圖2):

圖2

首先,若以第四節為整體,二分法是零點存在定理的深入和升華;若以必修一為整體,其核心內容是高中數學四大主線之一的函數,本節課作為函數的應用而展現,以函數的觀點認識方程,突出函數思想;若再以整個高中數學為整體,二分法的操作程序中蘊含算法思想,這將為必修三的學習做好鋪墊.其次,在學習本節課之前,學生對近似計算有所掌握,接觸過函數思想、數形結合思想,數學核心素養也有一定的發展水平.再次,高中生意志力增強,面對困難迎難而上,目標堅定努力上進,興趣廣泛而穩定,對新奇事物充滿探索欲.最后,教師應了解授課班級的精神風貌、班級學風,了解教室的空間布局、設備設施等.本節課涉及到特殊函數圖象、二分法迭代過程的體現,可借助GeoGeBra、幾何畫板等數學軟件予以直觀的呈現.

(2)“用二分法求方程的近似解”教學境脈具體設計

這節課采用復合型課堂結構,基于整體觀設計教學境脈:借助史料,引入二分法思想.通過生活情境,解釋求近似解的必要性并引出如何求近似解的問題.設計查找電路故障的情境,設計問題串,建立二分法思維.而后拆解二分法過程,總結定義與操作步驟,進行變式練習,接著回歸生活情境,反饋所學成果.課上還會介紹相關數學史、應用實例、思想方法、前后知識等,讓學生真正地學深悟透.如圖3.

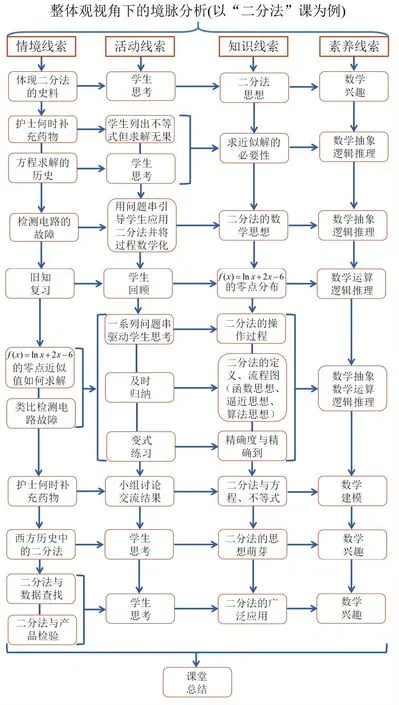
圖3

2.2 整體觀視角下“用二分法求方程的近似解”境脈教學實踐

環節1文化帶動,引入二分法思想

師:《道德經》中有“道生一,一生二,二生三,三生萬物”,《莊子》中有“一尺之棰,日取其半,萬世不竭”.這都體現了怎樣的思想呢?

學生回答,教師點評并解釋,引入二分法思想.

設計意圖引入體現二分法思想的古籍,激發學生興趣.

環節2為什么需要求方程的近似解

師:小王在12點30分時為病人注射了2500毫克的新型藥物.藥物的使用說明上標注了兩點:第一,只有在血液中藥物含量大于等于1500毫克時,藥物才能保持療效;第二,藥物在血液中以每小時20%的比例衰減.小王最晚需在幾時幾分之前再給病人補充藥物呢?

學生演算后回答,教師點評.

師:人類求解方程的歷史源遠流長.我們學習過一元一次方程、一元二次方程的解法,數學家不滿于此,探索高次代數方程,最終發現五次及更高次的代數方程沒有一般的求根公式.自然,包含ax、lnx等的超越方程也沒有求根公式.只需求方程的近似解.究竟該如何求方程的近似解呢?

設計意圖設置在學生最近發展區內的生活情境,引入不等式和方程,激發求知欲,借助方程求解的數學史,引出求近似解的必要性.

環節3采用什么方法求方程近似解

2023年7月末,超強臺風“杜蘇芮”強勢登陸廣東,某縣城的電力系統因臺風而出現故障.如果在由100段線路組成電路網中,有一處線路發生了故障.

問題1請問你會如何檢測故障點呢?

問題2采用什么方法才是最省時省力的呢?

問題3最多檢測幾次就可以確定故障點呢?

問題4你能否用數學語言表達檢測過程?

問題5這一方法是否可以被用來求方程近似解呢?

學生思考、計算后回答,教師點評并講解.

設計意圖通過創設生活情境,通過問題串,凸顯數學源于生活、寓于生活、用于生活.將檢測電路故障的二分法過程數學化,建立其與“用函數的思想求解方程”的數學聯系.

環節4溫故知新,回顧上節課所學

師:上節課對方程lnx+2x-6=0進行了初步探究,請同學們回憶一下.

學生思考并得出最終結論:f(x)=lnx+2x-6只有一個零點,且零點在區間(2,3)內.可列表,如表1,或畫函數圖象,如圖4(此函數圖象局部與直線相似).

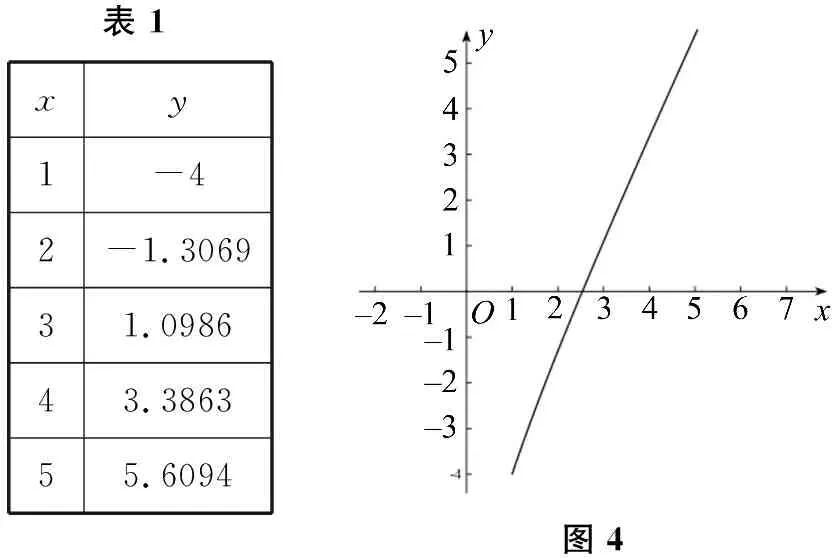
表1 xy1-42-1.306931.098643.386355.6094圖4

設計意圖接下來將對上節例題進行深入探究,體現教學的脈絡性.引導學生將新知與已有的認知結構產生聯系,同時這一步也體現了數形結合中的“由數到形”.

環節5脈脈相承,探索二分法步驟

師:下面要對這個零點做進一步的探究.如何才能求出這個零點的近似值呢?

生:首先縮小零點所在區間.

師:該如何進行縮小呢?剛才的二分法可以幫助我們解決這個問題嗎?

生:將區間(2,3)類比為電路網,零點類比故障點.這樣一來,就可以像尋找故障點一樣來求解零點近似值了.

師:非常好!類比尋找故障點的過程,第一步將區間一分為二取中點,中點為x=2.5.第二步,該如何判斷零點究竟是在(2,2.5)之間,還是在(2.5,3)之間呢?

生:這和判斷零點在(2,3)之間道理相同.首先計算中點函數的近似值,得f(2.5)≈-0.084.然后判斷區間中點和區間端點函數值乘積的符號,得f(2)f(2.5)>0,f(2.5)f(3)<0.由零點存在定理知,零點位于(2.5,3)之間.

師:但(2.5,3)這個區間還是相對較長,該如何做才能讓區間更加接近零點呢?

生:重復操作,不斷地取中點,將區間不斷地縮小.

師:用數學軟件給學生演示區間不斷縮小的過程.如圖5、6、7.

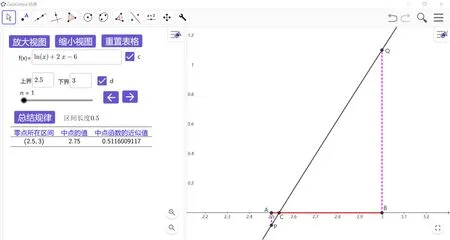
圖5

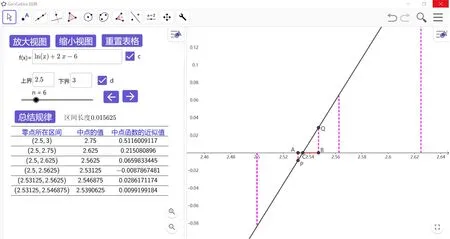
圖6

圖7

師:要二分多少次才能停止呢?換言之,需將區間縮小到什么程度才能停止呢?

生:像之前的近似計算,最終滿足題目給出的精確條件就可以了.

師:這里用精確度表示精確條件.對于給定的ε,零點近似值記作x0,零點精確值記作x,只要|x0-x|<ε,就代表滿足精確度.目前不知道x是多少,該如何判斷|x0-x|是否小于ε呢?

生:二者都在零點所在區間內.若區間長度小于ε,那區間內任意兩點之間的距離必然小于ε.

師:請大家用數學化的語言進行證明.

學生書寫證明過程,教師點評.

師:由此推出了一個滿足精確度的充分條件,即|a-b|<ε.

師:請同學們利用計算器求解f(x)=lnx+2x-6滿足精確度為0.01的近似值.

生:7次二分后區間長度恰好小于0.01.如圖8.區間(2.53125,2.5390625)內任意一點都可作零點近似值.也可將x=2.53125或x=2.5390625看作零點近似值.

圖8

設計意圖通過一脈相承的問題串引導學生探究.體現了數形結合中的“由形到數”,滲透了無限逼近的數學思想和程序化的算法思想.

環節6及時歸納,總結概念與方法

教師帶領學生概括二分法定義、用二分法求零點近似值的步驟及口訣.如圖9.

圖9

師:二分法定義中提到了逐步逼近,是數學中十分重要的思想方法.我國古代數學家劉徽的“割圓術”、之后將會學習的函數求導,其核心思想都是逐步逼近.

師:感興趣的同學課下可以了解程序框圖的知識,嘗試畫出二分法的程序框圖.

設計意圖概括二分法定義,培養學生抽象能力.強調逼近取極限的思想,為之后的學習積淀經驗,流程圖又展現出了算法思想,歸納總結能幫助學生建構整體的知識體系.

環節7變式練習,辨析終止的條件

借助計算器,用二分法求解以下方程的近似解.

0.8x-1=lnx,精確度為0.1;

2x+3x=7,精確度為0.1;

2x+3x=7,精確到0.1.

學生計算,教師點評并講解,著重區分兩個概念:精確度與精確到.

設計意圖借助變式練習區分相近概念,且變式練習可提高應變與應用的能力.

環節8情境再現,應用二分法解題

師:我們再來看最初小王遇到的難題,請大家小組合作得出最后的結果.

學生小組合作討論得出結論,并上臺展示,教師點評.

設計意圖完成整節學習的閉環,且這一問題涉及函數、方程、不等式,真正實現了知識的應用,增強學生分析問題和解決問題的能力.

環節9西方歷史中的二分法萌芽

在西方,二分思想同樣有所發展,芝諾悖論之一便是關于二分法的.感興趣的同學可在課下搜集資料,思考該如何來反駁芝諾的觀點呢?

環節10各個領域內的二分法應用

第一,二分法應用于數據查找.因其具備程序性和高效性,面對由數字或字母組成、數據龐大且排列有序的數組時,可以用二分查找法來確定某一特定元素.在厚重的字典中查找單詞,也可應用二分法.

第二,二分法應用于產品檢驗.大家可以思考如何利用二分法制定工廠檢驗次品的流程,且流程需具備可實施性、一定的準確性與高效性.

設計意圖適當補充相關知識可開拓學生視野,凸顯境脈的連續性與系統性.

環節11課堂小結,構建知識框架

師生進行本節課小結和整體知識框架的構建,如圖10、圖11.

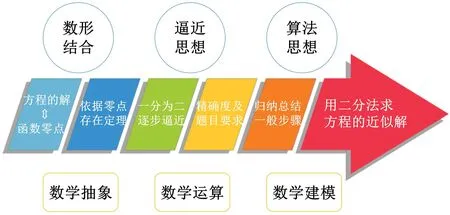
圖10

圖11

設計意圖有利于學生進一步理解、深入本節所學,以整體觀反思所學.

3 整體觀視角下數學境脈教學模式分析

好的教學設計不是一成不變的,而是全面吸收和整合利用各種資源的.整體觀視角下數學境脈教學模式,以學生為中心,將學生經驗、心理、知識與環境等各種因素都納入教學,從整體上進行全面綜合的教學設計,實現了“四跳出”,即“跳出講臺、跳出課堂、跳出教材、跳出教學”.跳出講臺,教師從知識的傳授者轉變為學習的組織者、引導者、合作者,不局限于三尺講臺;跳出課堂,從課前進行四條境脈分析及教學境脈搭建到課后及時反思,不局限于一方課堂;跳出教材,從學生經驗、數學核心素養發展、知識應用、發展脈絡、跨單元跨學段跨學科等方面整體設計,不局限于一本教材;跳出教學,從學生心理特點、學生認知特點、班風班紀、學習環境及設備等角度綜合分析,不局限于原來某一種模式的教學.

本教學模式有以下特點:①豐富教學內容,激發課堂活力.因為整體宏觀視角的指導,教師在備課時需要籌備比傳統教學更多更廣的內容,并以喜聞樂見的情境形式進行課堂導入,吸引學生持久的注意力,營造課堂活躍的學習氛圍.②重塑課堂生態,重視學習體驗.在境脈教學中,學生的主體地位得以鞏固,且數字化在數學課堂中逐漸占有一席之地,教師要學會協調自身、學生和數字化三者之間的關系,打造課堂新形態.③指向完整的人,指向連續發展的社會.整體觀指導下的境脈教學,其優勢在于以學生為中心統籌教學的廣度、深度、完整性和連續性,使學生的數學核心素養得到全面鍛煉、連續發展與螺旋提升.

4 教學實施建議

整體觀視角下境脈教學實施的關鍵在于教師如何鋪設各路境脈,這需要教師在實踐中不斷探索、總結與優化.需要注意以下幾個方面:

①積累素材,靈活運用.為了構建境脈,教師應關注并挖掘學生感興趣的、當下時興的、有教育價值的話題與事物,依據教學需要合理創設情境,切忌生搬硬套、冷門偏僻.

②通宏洞微,循序漸進.教師既需要從宏觀的知識體系出發,還需要著眼于每一個知識點的掌握,為了讓知識以脈絡的形式貫穿課堂,教師應循著知識的發展過程設計教學.

③整體洞察,協作創新.境脈教學的結構、內容豐富多樣,這要求教師對學生、教材、課標等必須了如指掌,對教師的教學功底也有一定要求.教師之間要加強溝通交流,取長補短,合作優化教學模式.