深海能源土含氣儲層邊坡穩定性研究

王 瀅,王妍妍 ,高 盟,張 糧

(1.山東科技大學 山東省土木工程防災減災重點實驗室,山東 青島 266590;2.山東科技大學 土木工程與建筑學院,山東 青島 266590)

深海能源土作為21世紀最具開發前景的新型戰略性替代能源,其開采利用價值及開發前景極為廣闊。然而能源土開采不當所引發的安全和生態環境問題仍是當前亟需解決的難題。現有對能源土含氣儲層的研究大多為對固態水合物的分析,未考慮水合物分解形成的含氣儲層的影響。同時,能源土大多儲存在海底沉積物邊坡中,其開采過程會對海底邊坡的穩定性造成重要影響。

隨著海底邊坡穩定性研究的持續深入,涌現出大量的研究成果。Mackillop等[1]通過確定性和概率性方法評估海底斜坡穩定性,得出循環荷載(地震)或預處理因素(孔隙壓力的升高)是斯科蒂安斜坡失穩的關鍵。Cao等[2]基于有限元Abaqus對海底滑坡進行數值模擬,得出陸地邊坡的安全系數是海底邊坡的5～10倍,海底邊坡滑帶范圍更寬、更深,滑帶邊界不明顯。Nian等[3]采用極限分析的運動學方法考慮波浪誘導壓力下的海底斜坡穩定性,得出波浪對邊坡穩定性的影響規律。Chu等[4]計算了曹妃甸典型海底斜坡在發生類似唐山地震時的動力響應,得出位移值可定量反映地震對場地斜坡的影響。成瑋等[5]以淤泥質海底航道邊坡為研究對象,開展了基于淺剖的邊坡失穩滑塌模擬實驗、邊坡失穩演變過程分析等研究,得出淤泥質海底航道邊坡穩定性變化規律。歐陽敏等[6]基于FLAC 3D數值模擬方法并應用強度折減法進行海底邊坡穩定性計算,得出土體強度是海底邊坡穩定性評估的重要影響因素。

開采利用能源土將誘發長期的巨大的地質災害及壞境風險,海底滑坡為典型表現形式,國內外學者進行了大量的研究。Zhao等[7]提出了“兩步折減法”用于評估初始地應力平衡和水合物分解對基底強度折減的影響,認為水合物分解可以觸發海底滑坡,特別是沿著滑動面。其他研究也顯示,水合物分解是誘發海底滑坡的主要影響因素[8-9]。唐常銳等[10]通過Gassmann方程計算出儲層的孔隙度和飽和度,并反演出其他巖土物理參數,利用數值模擬方法得出水合物分解程度是影響海底邊坡穩定性的主要因素。徐斌等[11]采用時間變化參數的摩爾庫倫本構模型及應力釋放法,通過自寫程序對海底邊坡穩定性進行數值分析,得出水合物分解導致的強度衰化和模量軟化是導致海底斜坡和位移發生變形和沉降的原因。以上研究大多針對導致能源土儲層邊坡失穩的外部因素,且沒有考慮土體組分含量的影響。

本研究以深海能源土采挖回填裝置[12]為依托,基于前期實驗室固結排水三軸壓縮剪切試驗[13]得到的深海能源土相關力學參數,采用有限元強度折減法建立深海能源土含氣儲層邊坡模型,探究深海能源土含氣儲層在勘察、開采及回填3種工況下,不同黏土含量、含氣量及回填加固對深海能源土邊坡穩定性的影響。

1 模型建立

我國南海北陸坡白云凹陷區和珠江口盆地的峽谷區存在陡坡,坡度達到40°左右[14]。陡坡穩定性差,對外界擾動更加敏感,更容易發生滑坡失穩。因此,以深海能源土采挖回填裝置[12]的開采工況為實際工程背景,該裝置主要采用將深海能源土固態儲層變為含氣儲層的方法進行開采,其開采全過程將遇到極為復雜的巖土工程問題。因此,依據開采形成的海底地質構造,將能源土開采工況大致分為以下3種:工況1(裝置勘探階段)。勘探過程中的海底邊坡不一定含有能源土,且大多為海底沉積物土體,此時的構造類型為不包含能源土的海底沉積物邊坡;工況2(裝置開采階段)。由于開采裝置的影響,能源土固態儲層變為含氣儲層,即深海能源含氣土層的海底沉積物邊坡;工況3(裝置開采后的回填階段)。開采裝置通過回填機構向采空后的土層灌入回填環保材料,此時能源土土層變為回填土層,構造類型設定為包含回填土層的海底沉積物邊坡。

1.1 模型尺寸

參照劉芳等[15]所建海底水合物邊坡模型,模擬我國南海北陸坡水合物富集區的典型45°陡坡,開采工況幾何模型如圖1所示。參考開采工況下邊坡的構造情況,邊坡模型尺寸設置為:橫跨長度為800 m,上、下坡面跨度為300 m,坡頂水深2 000 m,坡底水深2 200 m,下坡面高200 m,上坡面高400 m。深海能源土含氣夾層埋深設為30 m,厚度為30 m,夾層同坡面平行。

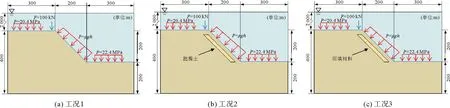
圖1 深海能源土含氣儲層邊坡幾何模型示意圖

除探究深海能源土含氣儲層邊坡穩定性外,還對勘探及回填階段的海底邊坡進行了穩定性分析。本研究所建邊坡模型為簡化模型,僅考慮海水壓強、土體自重和開采引起的外部荷載3個因素,不考慮波浪、暗流等動荷載的影響。依據水深壓強計算公式P=ρgh計算海水壓強大小,使其均勻分布在海床表面。其中:ρ為海水密度,取1.02×103kg·m-3;g為重力加速度,取10 m·s-2;h為海水深度。施加在能源土夾層正上方海床表層處的外部荷載采用點荷載(F),取值為100 kN。

1.2 計算參數

參考Masuda等[16]對南海海漕原位開采巖芯試樣進行的水合物分解試驗研究,并結合前期實驗室三軸壓縮固結排水剪切試驗得出的相關理論[13],根據《土工試驗方法標準》[17],取部分配比的海洋土試樣進行物理參數指標測定,測定結果如表1所示。在回填工況下采用膠結性環保材料(聚氨酯泡沫膠黏劑)加固的土體參數由實驗室測得,值得注意的是,開采階段和回填階段僅展示夾層參數,周圍土體參數采用勘探階段時黏土含量為3%的海洋土沉積物參數,模型參數見表2。

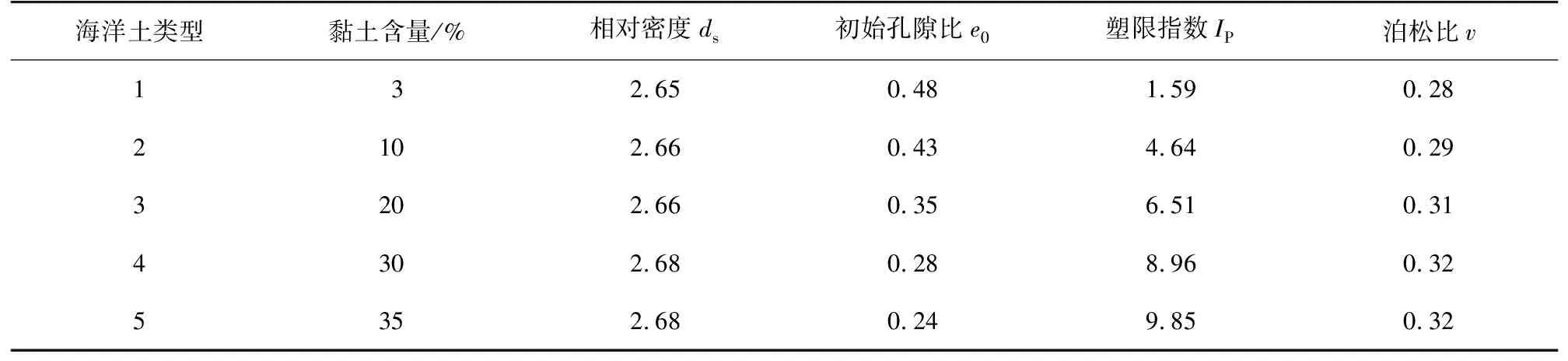
表1 海洋土土樣基本物理力學指標

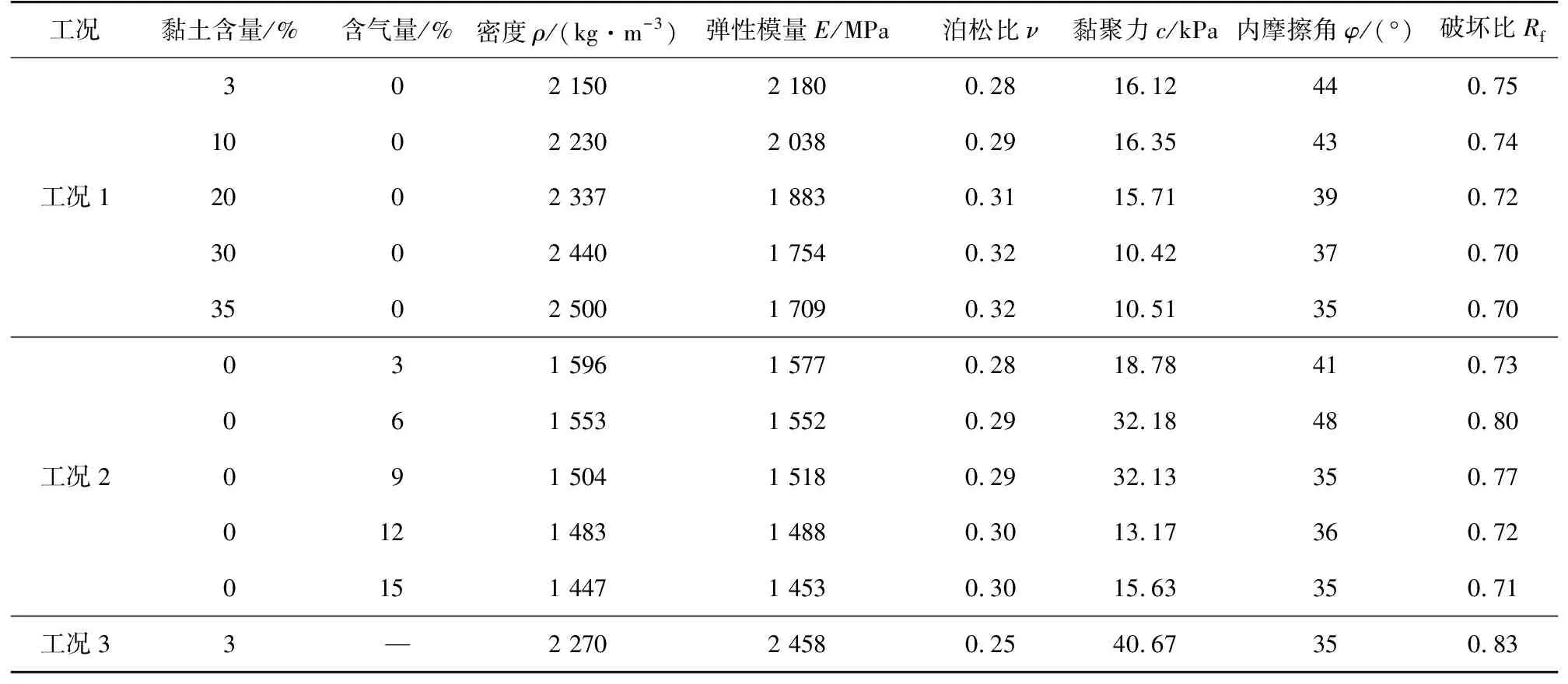
表2 模型參數表

1.3 邊界條件

采用ABAQUS有限元軟件,依據幾何模型尺寸建立二維邊坡有限元模型,對不同工況下海底邊坡的穩定性進行數值模擬研究。為解決在實際海底環境中,海床跨度大使得有限元計算效率大大降低等問題,將海床視為一個半無限空間體,即將海床底部及其兩側視為無限土體,模型左右側和底部邊界條件均為無限邊界,頂部和斜坡邊界為海水壓力和開采壓力。安全系數可視為邊坡失穩臨界值,超過安全系數可視為邊坡失穩。采用無限元人工邊界模擬地基半無限空間,與有限元部分統一求解,不涉及解析表達式,不僅能縮小計算規模,還能保證計算精度。

基于有限元理論對幾何模型進行網格劃分,二維邊坡計算模型如圖2所示。紅框包圍部分為所設無限元人工邊界,其余部分為邊坡有限元模型,為得到海底邊坡的安全系數,對坡頂夾角處的單元點進行監測,取其總位移同安全系數關系曲線的拐點作為邊坡失穩點,所對應的折減系數[18]即為邊坡安全系數,超過這一系數則視為土體失穩。本研究主要探討邊坡的臨界失穩狀態,因此只對邊坡失穩時瞬態的有效塑性應變及位移云圖進行分析,對滑坡之后的土體演變過程暫不深究。

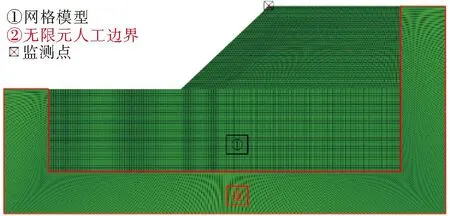
圖2 二維邊坡計算模型

1.4 模型驗證

為保證深海能源土二維邊坡模型的準確性及有效性,需特別注意初始應力的平衡問題,而深海能源土在實際開采階段,所受的應力主要來自土體自重、海水壓強和開采引起的外部荷載。因此,針對深海能源土含氣儲層邊坡模型進行相應的初始應力平衡,模擬海底邊坡的真實開采環境。

采用自動平衡法實現深海能源土邊坡的初始應力平衡,所施加的初始應力場如圖3 所示。一般認為,初始應力平衡后的土體位移數量級小于1×10-4m,即滿足初始應力平衡要求。初始應力平衡后模型的最大位移為 5.622×10-10m,遠遠小于規定的數量級,間接證明了模型的準確性及有效性。

圖3 初始應力場

2 不同工況下深海能源土含氣儲層邊坡穩定性變化規律

2.1 不含能源土的海底沉積物邊坡穩定性變化規律

圖4為工況1邊坡有效塑性應變云圖。由圖4可知,不同黏土含量下的海底沉積物邊坡均出現應力失穩滑動面,且均從坡腳處開始,并在某一時間產生二次滑動。同時,各黏土含量下的最大有效塑性應變分別為9.376%、12.07%、13.26%、13.98%和17.65%,表明邊坡的最大有效塑性應變隨黏土含量的增大呈上升趨勢,黏土含量對邊坡失穩破壞的影響顯著。

圖4 工況1邊坡有效塑性應變云圖

圖5為工況1邊坡總位移云圖。由圖5可知,海底沉積物邊坡自坡腳處開始出現明顯的位移滑動,并逐漸蔓延到邊坡下部土體。同時,黏土含量越高邊坡總位移云圖的土體位移滑動范圍越廣,越容易影響到邊坡下部土體的穩定性,嚴重時將引發地震等重大地質災害。此外,各邊坡的最大位移值受黏土含量的影響顯著,各黏土含量的邊坡最大位移值分別為14.15、16.64、17.99、16.54和19.54 cm,黏土含量越高,所對應的最大位移值就越大。因此,在實際開采過程中應對海底沉積物進行勘探,并對其黏土含量進行分析,以制定不同的開采方案來保障深海能源土的安全開采。

圖5 工況1邊坡總位移云圖

圖6為工況1邊坡安全系數同坡頂位移關系曲線。由圖6(a)～圖6(e)可知,在將兩段曲線進行擬合時,其擬合線的交點即為曲線拐點,則各黏土含量的邊坡安全系數Fr分別為1.22、1.21、1.10、1.01和0.96,安全系數隨黏土含量的增加呈逐漸下降的趨勢,表明黏土含量越高土體邊坡的承載能力越低,即安全系數越低,邊坡的穩定性越差[18],證明隨著黏土含量的增加,深海能源土含氣儲層邊坡穩定性越差。圖6(f)為將邊坡安全系數隨黏土含量的變化進行線性擬合,得到的黏土含量-安全系數關系曲線,可為深海能源土的勘探及開采設計提供參考。

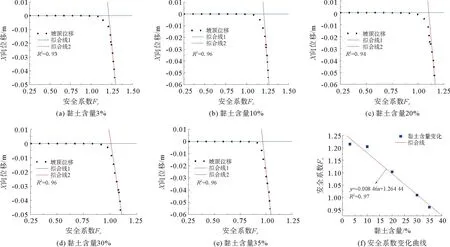
圖6 工況1邊坡安全系數與坡頂位移關系曲線

2.2 含氣量對海底沉積物邊坡穩定性的影響

采用負壓法[19-20]開采能源土時,固態能源土將變為含氣土,儲層原有的應力平衡狀態發生改變。因此,需對賦存能源含氣土的海底邊坡進行穩定性分析,以探知開采裝置在能源土開采過程中土體邊坡的力學變化規律。

圖7為工況2邊坡有效塑性應變云圖。由圖可知,能源土含氣儲層的含氣量對海底邊坡穩定性的影響較為明顯,由低到高各含氣量下海底邊坡所對應的最大有效塑性應變分別為25.88%、17.45%、22.6%、27.81%和32.37%,應變峰值隨含氣量的增加呈先下降后增大的趨勢,這主要是因為6%、9%含氣量的能源含氣土黏聚力較大,導致土體顆粒之間的膠結作用增強,進而降低了海底邊坡的有效塑性應變。此外,能源土含氣儲層邊坡失穩僅在賦有能源含氣土的區域發生滑動,且滑動面主要以賦存區域與周圍土體的接觸面為主,這說明能源土賦存區域的強度變化對邊坡穩定性的影響更為劇烈。因此,在進行開采設計時應特別注意對能源土賦存區域的穩定性處理。

圖7 工況2邊坡有效塑性應變云圖

圖8表示工況2邊坡總位移云圖。如圖8所示,由低到高不同含氣量下深海能源土含氣儲層邊坡的總位移峰值分別為19.40、15.96、18.12、22.35和24.74 cm,同有效塑性應變所得結論相同,均呈先減小后增大的變化規律。此外觀察含氣量6%、9%的邊坡位移云圖可以發現,同周圍土體相比,其黏聚力的增大導致能源土位移更小,且土體位移主要以能源土上覆土體位移為主。

圖8 工況2邊坡總位移云圖

圖9表示工況2邊坡安全系數與坡頂位移關系曲線。由圖9可知,含氣量由低到高各邊坡的安全系數分別為1.20、1.31、1.29、1.01和0.99,安全系數隨含氣量的增加呈先上升后下降的變化趨勢。這表明含氣量6%、9%下能源土含氣儲層邊坡的承載能力變強,但隨著含氣量的增加該現象逐漸消失,這一規律同有效塑性應變、總位移云圖所得結論一致。由上述規律可知,含氣量對深海能源土含氣儲層邊坡安全系數的影響不再呈單一變化規律,對其關系曲線進行非線性擬合處理,可得擬合公式為:

(1)

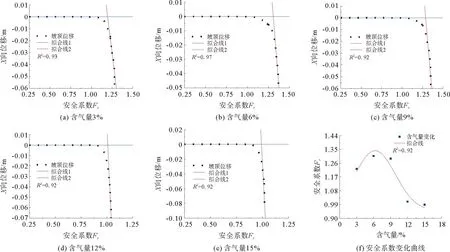
圖9 工況2邊坡安全系數與坡頂位移關系曲線

其中:x為含氣量;e為常數,取2.718;π取3.141。

2.3 回填加固處理對海底邊坡穩定性的影響

深海能源土采挖回填裝置中能源土開采后,甲烷氣體被收集,原氣體賦存區域的土體孔隙慢慢充入水或成為真空狀態,增加發生海底滑坡等地質災害的幾率。因此,需對開采后的能源賦存區域充入回填材料,以確保海底邊坡維持原有的穩定性。

本研究采用膠結性環保材料對深海能源土儲層進行回填處理,圖10(a)為工況3海底邊坡有效塑性應變云圖。由圖10(a)可知,土體沿能源土賦存區域邊界產生滑動面,坡腳處產生最大塑性應變,約為9.5%,其有效塑性應變峰值均低于能源土含氣儲層邊坡。此外,由圖10(b)工況3邊坡總位移云圖可知,邊坡失穩后的位移主要發生在回填層上覆土體區域,對于回填層及下部土體的影響較小,且總位移峰值為14.54 cm,遠遠小于能源土含氣儲層邊坡位移峰值。

圖10 工況3邊坡有效塑性應變云圖和總位移云圖

圖11為工況3邊坡安全系數與坡頂位移關系曲線。由圖11可知,回填處理后的海底邊坡安全系數為1.33,高于其他兩種工況下海底邊坡的安全系數,滿足海底邊坡的穩定性要求。綜上所述,充入膠結性回填材料對能源土含氣儲層的邊坡穩定性具有積極作用,直接證明了采用回填處理的方法加強海底邊坡的穩定性是可行的。

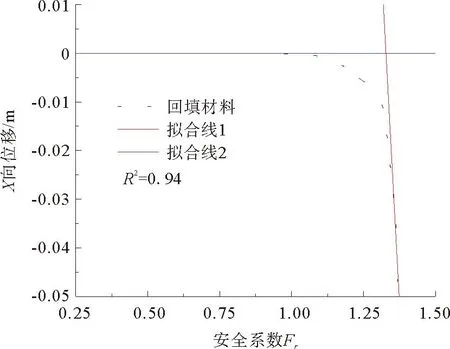
圖11 工況3邊坡安全系數與坡頂位移關系曲線

3 結論

以深海能源土采挖回填裝置所設的勘察、開采及回填3種工況為背景,基于強度折減法建立海底邊坡模型,探究深海能源土邊坡在不同黏土含量、含氣量以及回填加固條件下的穩定性,得出結論如下。

1) 黏土含量變化對海底沉積物邊坡穩定性的影響效果顯著,邊坡有效塑性應變峰值和總位移峰值隨黏土含量的增加而逐漸增大,黏土含量越高的邊坡安全系數越低,越容易發生海底滑坡等地質災害。

2) 深海能源土含氣儲層邊坡穩定性隨含氣量增加呈非線性變化規律,邊坡有效塑性應變峰值和總位移峰值隨含氣量的增加呈先下降后上升的變化趨勢;安全系數變化與之相反,呈先升高后下降的趨勢,這表明一定儲量范圍的深海能源土含氣儲層對海底邊坡的穩定性具有強化作用。

3) 采用膠結性環保材料對開采后的能源土含氣儲層進行回填處理能夠有效提高海底邊坡的穩定性,對能源土開采所帶來的地質災害及環境污染問題的防治具有重要意義。