拖掛式移動機器人的多約束避障軌跡規劃

宋保業,吳 尤,田運陽,許 琳

(山東科技大學 電氣與自動化工程學院,山東 青島 266590)

拖掛式移動機器人(tractor-trailer mobile robot,TTMR)是一種由牽引車和掛車組成的復雜多體機械系統,能夠根據應用場景靈活改變掛車的數量,具有較強的運載能力。目前,TTMR的應用場景有大型機場的行李運輸,火車站、貨運港口的貨物運輸,自動化工廠的物料運輸等[1-3]。在各種應用場景中,沿結構化道路行駛的TTMR需要對道路上出現的障礙物進行避障,考慮避障過程需要滿足的平穩性、舒適性和交通效率等,研究TTMR在多約束條件下以最優避障時間和最優避障距離完成避障軌跡規劃,對提高TTMR的作業效率具有重要意義。

由于TTMR具有特殊的結構特征,在前向和后向運動時存在不同的運動機理[4-5],所以在進行避障軌跡規劃時需要考慮以下因素:為了避免車體間發生折疊現象,牽引車與掛車之間的鉸接角必須限制在合理范圍內;考慮到牽引車驅動電機的響應特性,系統的控制輸入存在明顯的飽和約束;為了保證系統在橫向上無滑移現象,牽引車車輪和掛車車輪均滿足非完整約束條件。

TTMR避障軌跡規劃研究得到了國內外學者的大量關注。文獻[6]為實現TTMR多障礙場景下的軌跡規劃,基于生成對抗網絡 (generative adversarial networks,GANs)和直接軌跡規劃(direct trajectory planning,DTP)建立了GDTP模型,并將該模型嵌入到快速搜索隨機樹(rapidly-exploring random tree,RRT)中進一步設計了GDTP-RRT算法,多場景實驗驗證了該算法具有高可靠性,但算法的性能和效率有待進一步提高;文獻[7]基于半監督學習提出一種新的TTMR路徑規劃方法,其關鍵是構造一個路徑代價函數并通過編碼器—解碼器類型的深度神經網絡訓練,但由于深度學習方法的概率特性,該方法很難實現100%的路徑可行性;文獻[8]提出一種基于凸多邊形形式的TTMR避障路徑規劃方法,通過Farkas引理將表示TTMR和周圍環境的多個凸多邊形對象轉換為無碰撞約束,并將這些約束與目標函數結合后求解最優化問題,但是尋找適合所提方法的求解器比較困難;文獻[9]為了實現TTMR自動泊車,改進了混合A*搜索算法,提出雙向A星-搜索導引樹(bi-directional A-search guided tree,BIAGT)算法,通過硬件在環仿真驗證了算法的有效性,但該算法的搜索完整性不足。近年來,由于多項式軌跡規劃方法便于算法擴展,且規劃的參考軌跡僅與系統的初末狀態有關,因此在許多領域得到了應用[10-12]。文獻[13]采用三次多項式設計滿足自主車輛運動學約束的移動路徑,設計的曲線路徑易于軌跡跟蹤控制器的實現,但曲線路徑一旦設計完成不易調節,并且多項式系數的微小噪聲會造成曲線形狀的較大變化;文獻[14]提出基于時間的五次多項式函數規劃參考軌跡,仿真結果表明五次多項式函數生成的參考軌跡更簡單、平滑,無尖銳點和突變點等,但是沒有考慮系統初末位置的橫向、縱向急動度以及軌跡曲率、曲率導數的約束。

針對上述問題,本研究在速度、加速度、急動度、曲率及曲率導數等多約束條件下,基于七次多項式函數研究了拖掛式移動機器人的避障軌跡規劃問題。選取的優化目標函數同時考慮了最優避障時間和最優避障距離,能夠滿足避障過程中對機器人平穩性、舒適性和交通效率的要求。通過仿真對比實驗,驗證了提出的多約束條件下拖掛式移動機器人的避障軌跡規劃方法的有效性。

1 拖掛式移動機器人數學建模

1.1 TTMR系統描述

TTMR系統由兩節車體組成,前一節為差速驅動轉向的牽引車,后一節為無動力源的掛車,兩節車體之間通過一個剛性軸采用標準鏈接方式連接。標準鏈接方式是指相鄰兩車體的鏈接點在前一車體驅動輪軸的中心點上。此外,牽引車安裝有兩個受獨立電機驅動的主動輪和一個可沿任意方向移動的用來維持車體平衡的萬向輪。整個系統通過牽引車左右兩個獨立電機提供的輸出扭矩以實現對掛車車輪軸中心點K的控制,TTMR系統結構如圖1所示。圖1中,P和Pc表示牽引車車輪軸中心點和牽引車車體的質心點;K表示掛車車輪軸中心點;b表示兩平行車輪間距的一半;d和l分別表示P與K、P與Pc之間的距離;(x,y)和(x1,y1)分別表示K和P在全局坐標系下的坐標;φ和θ分別表示牽引車和掛車的航向角。

圖1 TTMR系統結構

為了方便研究作以下假設:TTMR由剛性構件組成;車輪在移動時為純滾動,不發生滑移;每個車體的車輪與地面均為單點接觸;不考慮內部阻尼與電機動態特性的影響。

1.2 運動學模型

1) 前向運動時的運動學模型

基于車輪移動時純滾動、無滑移的假設,系統存在非完整約束條件為:

(1)

引入廣義坐標系q=[x,y,φ,θ]T,對TTMR的位置和姿態信息進行描述。定義u=[υ,ω]T為系統的輸入向量,υ為牽引車在P點的線速度,ω為牽引車的角速度,得到TTMR前向運動時的運動學模型為:

(2)

2) 后向運動時的運動學模型

當TTMR后向運動時,系統存在非完整約束條件為:

(3)

計算可得TTMR后向運動時的運動學模型為:

(4)

2 避障軌跡規劃

2.1 避障軌跡設計

由于多項式軌跡規劃方法只需知道系統的初始狀態和最終狀態,不需考慮系統的中間過程,并且多項式函數本身及其一階、二階、三階導數均是光滑的,這使得差速驅動的移動機器人在軌跡跟蹤過程中無需在不同狀態之間頻繁切換[15]。此外,考慮車體在移動過程中的平穩性,狀態開關的急動是不允許的[16]。因此,本節基于多項式理論對TTMR的避障軌跡進行設計。

對于TTMR的避障軌跡規劃,原則上需要分別對牽引車和掛車的避障軌跡進行規劃。然而,假設掛車的避障軌跡為(x(t),y(t)),通過圖1所示的TTMR系統結構可以得到:

(5)

因此,只需規劃出掛車的避障軌跡,即可通過方程組(5)獲得牽引車的避障軌跡。TTMR的前向避障過程和后向避障過程分別如圖2、圖3所示。

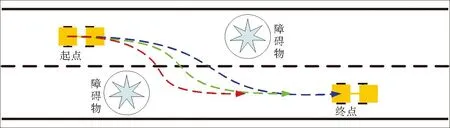
圖2 前向避障過程

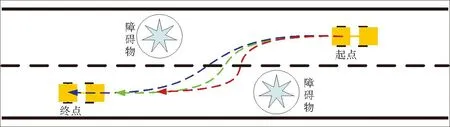
圖3 后向避障過程

考慮到避障過程中的穩定性和舒適性,需要對TTMR初/末位置的橫向和縱向速度、加速度、急動度以及避障軌跡的曲率和曲率導數等進行約束。根據七次多項式函數中含有的未知數個數可知,求解所需方程數為8個。由于本研究考慮了TTMR在初/末位置的速度、加速度、急動度等共8個狀態向量,可對應8個含有未知數的多項式方程,所以在x方向和y方向選用七次多項式作為避障軌跡,并對結構化道路下的避障場景作以下假設:TTMR始終沿道路中心行駛且障礙物也在道路中心;避障軌跡的起點與坐標系原點重合;避障過程中無其他車輛的影響;車載傳感器能夠在安全避障距離xs以外檢測到障礙物。

在x方向和y方向選用七次多項式為:

(6)

對方程組(6)求一階、二階、三階導數,代入系統的初始狀態向量和最終狀態向量得:

(7)

式中:a=[a0,a1,…,a7],b=[b0,b1,…,b7],

給定系統的初始狀態和最終狀態為:

(8)

式中:xf表示TTMR的避障距離;yf表示TTMR行駛的橫向位移,由于TTMR始終沿著道路中心運動,所以yf等于道路的寬度W。

將初始狀態與最終狀態代入方程組(7)解得多項式系數,最終只需確定W、υ0、xf、tf這4個未知參數即可確定一條避障軌跡:

(9)

2.2 系統約束條件

考慮到牽引車兩個驅動電機的響應特性,系統的控制輸入受到明顯的飽和約束,因此需要對TTMR的實際行駛速度進行限制:

(10)

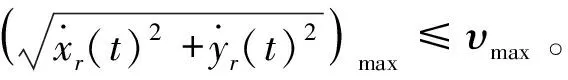
(11)

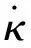
(12)

(13)

(14)

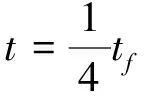
(15)

需要注意的是,為了使生成的后向避障軌跡比前向避障軌跡更平滑,防止因TTMR的鉸接角過大導致兩節車體陷入危險的折疊狀態而失去穩定性,系統約束條件(10)～(15)在實際應用中可適當降低。

2.3 求解目標函數

根據方程組(9)可知,只需確定W、υ0、xf、tf這4個未知參數的取值,即可確定一條避障軌跡。避障過程是否安全受到避障時間tf和避障距離xf的直接影響,因此隨意地給tf和xf賦值是不可取的[17]。同時兼顧避障過程中平穩性、舒適性、交通效率的要求,選取目標函數為:

(16)

式中:g1、g2和g3表示正的權重因子,g4表示正常數。因此基于系統約束條件(10)～(15)和目標函數(16),含有不等式約束條件的優化問題可以描述為:

(17)

3 仿真結果與分析

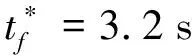
表1 前向避障時的權重系數和約束條件

圖4 前向避障軌跡規劃結果

圖5 前向避障時的多項式曲線各參數變化

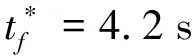
表2 后向避障時的權重系數和約束條件

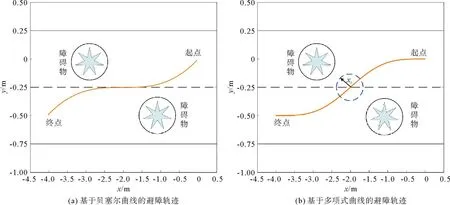
圖6 后向避障軌跡規劃結果

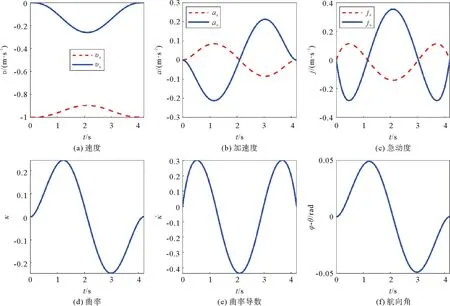
圖7 后向避障時的多項式曲線各參數變化

4 結論

本研究針對TTMR沿結構化道路前向和后向運動時躲避障礙物的避障軌跡規劃進行了研究。首先,在保證系統非完整約束的前提下,分別建立了TTMR前向和后向運動時的運動學模型;然后,基于七次多項式函數分別規劃了TTMR前向和后向避障軌跡,并引入約束條件和目標函數對避障時間和避障距離進行優化;最后,使用MATLAB對所規劃的避障軌跡進行對比仿真驗證。仿真結果表明,在多約束條件下采用七次多項式函數作為TTMR的避障軌跡是一個較佳的選擇。基于七次多項式曲線的避障軌跡規劃方法能夠顯著提高TTMR沿結構化道路行駛時的避障能力,可以為鉸接式車輛的相關研究提供理論借鑒。