四旋翼飛行器多模式穩(wěn)定控制

賈曉涵,付麗霞

(昆明理工大學(xué) 信息工程與自動化學(xué)院,昆明 650500)

0 引 言

四旋翼飛行器具有體積小,結(jié)構(gòu)簡單,可以靈活地懸停和垂直起降等優(yōu)點,被廣泛應(yīng)用于軍事和民用領(lǐng)域.近年來,四旋翼飛行器的軌跡跟蹤控制問題受到各國學(xué)者的廣泛關(guān)注.要使四旋翼飛行器有良好的飛行品質(zhì),具有良好的軌跡跟蹤性能固然重要,但是保證飛行器的姿態(tài)穩(wěn)定也很有必要.

四旋翼飛行器具有非線性、強耦合和欠驅(qū)動等特性.在飛行過程中,螺旋槳的高速轉(zhuǎn)動會對機體帶來較大震動,且在組裝四旋翼飛行器的過程中無法做到完全對稱,故難以建立其精確的數(shù)學(xué)模型,而且四旋翼飛行器易受擾動的影響,因此建模的誤差與外部擾動均會對系統(tǒng)產(chǎn)生較大的消極影響,這使得其控制器的設(shè)計面臨很多的問題.針對四旋翼飛行器的控制問題,國內(nèi)外學(xué)者提出了多種有效的控制策略.文獻[1,2]分別使用分數(shù)階PID以及PID與自適應(yīng)算法融合的控制方案,可以完成簡單的軌跡跟蹤,但由于四旋翼飛行器屬于非線性系統(tǒng),在復(fù)雜軌跡跟蹤時,采用線性的控制方法會使控制精度明顯下降.為解決該問題,學(xué)者們提出了多種非線性控制方法,文獻[3]采用非線性魯棒控制方法來實現(xiàn)路徑跟蹤任務(wù),在存在不確定擾動的情況下保證了軌跡跟蹤的精度和魯棒性;文獻[4]提出了一種基于優(yōu)化濾波器的自適應(yīng)輸出反饋控制方法,并通過軌跡跟蹤實驗證明了其具有良好的魯棒性;文獻[5]提出了一種參數(shù)調(diào)度反步法控制器,通過實驗驗證了其有效性.但以上論文僅考慮了四旋翼飛行器軌跡跟蹤的精度與魯棒性,未考慮飛行器軌跡跟蹤過程中的姿態(tài)穩(wěn)定問題.

由于四旋翼飛行器的欠驅(qū)動特性[13],無法對6個自由度均進行設(shè)定值跟蹤,通常采用的控制方案[16]是對位置以及偏航角設(shè)定期望值進行跟蹤,對所需要的俯仰角和滾轉(zhuǎn)角進行求解并跟蹤.四旋翼飛行器易受擾動的影響,如果求解所得姿態(tài)角度過大或過小時,仍對其進行跟蹤會使飛行器飛行不穩(wěn)定,存在一定安全隱患.針對該問題,本文提出了一種多模式切換控制策略,以提升飛行器的穩(wěn)定性,系統(tǒng)采用內(nèi)外環(huán)控制,內(nèi)環(huán)為姿態(tài)控制環(huán),外環(huán)為位置控制環(huán).位置子系統(tǒng)采用自適應(yīng)RBF神經(jīng)網(wǎng)絡(luò)非奇異終端滑模控制器對期望位置進行跟蹤;在姿態(tài)子系統(tǒng)中,首先設(shè)定四旋翼飛行器的姿態(tài)安全區(qū)間,對超出該區(qū)間的姿態(tài)角度設(shè)置邊界期望值,并求解其余兩姿態(tài)角期望值,然后,采用超螺旋非奇異終端滑模控制器對期望姿態(tài)角進行跟蹤.最后,通過仿真實驗驗證了該控制策略的有效性.

1 四旋翼飛行器模型

首先,針對四旋翼飛行器的結(jié)構(gòu),建立慣性坐標系e與飛行器坐標系b,如圖1所示.

圖1 四旋翼飛行器結(jié)構(gòu)示意圖Fig.1 Structural diagram of uav

其中,θ、φ、ψ表示的是飛行器3個姿態(tài)角:俯仰角、滾轉(zhuǎn)角和偏航角;R1～R4為飛行器的4個螺旋槳,任意相鄰的兩個螺旋槳的轉(zhuǎn)向相反;4個螺旋槳所產(chǎn)生的升力為F1～F4;飛行器共有4個控制輸入量為U1～U4,分別代表垂直速度控制量、滾轉(zhuǎn)角控制量、俯仰角控制量和偏航角控制量,控制量與升力的關(guān)系為:

(1)

其中,l為每個螺旋槳中心距飛行器質(zhì)心Ob的距離.

由牛頓-歐拉方程,可得四旋翼飛行器數(shù)學(xué)模型為:

(2)

其中,x、y、z為飛行器在慣性坐標系中的位置坐標;Ix、Iy、Iz為繞機體坐標系的Xb、Yb、Zb軸的轉(zhuǎn)動慣量;m為飛行器質(zhì)量;g為重力加速度;fx、fy、fz為未知干擾.

2 控制系統(tǒng)設(shè)計

系統(tǒng)采用內(nèi)外環(huán)控制的方法.外環(huán)為位置控制環(huán),通過自適應(yīng)RBF神經(jīng)網(wǎng)絡(luò)對未知擾動進行預(yù)測,由位置子系統(tǒng)的控制器得到垂直速度控制量U1輸出到位置子系統(tǒng),同時初步解算出所需要的期望姿態(tài)角度φd0、θd0;內(nèi)環(huán)為姿態(tài)控制環(huán),根據(jù)初步解算的期望姿態(tài)角進行控制模式選取,并重新解算3個姿態(tài)角度的期望值φd、θd、ψd,通過姿態(tài)子系統(tǒng)的控制器得到姿態(tài)角控制量U2、U3、U4輸出到姿態(tài)子系統(tǒng).控制系統(tǒng)結(jié)構(gòu)圖如圖2所示.

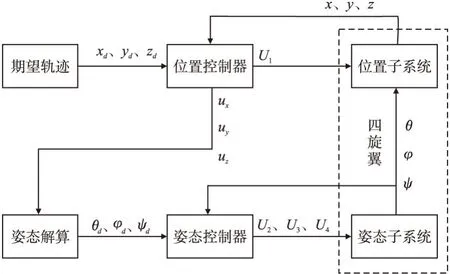
圖2 控制系統(tǒng)結(jié)構(gòu)圖Fig.2 Control system structure diagram

2.1 位置控制器設(shè)計

對位置子系統(tǒng)控制器進行設(shè)計.首先,定義位置控制器虛擬控制量ux、uy、uz為:

(3)

根據(jù)式(2)、式(3),則位置子系統(tǒng)模型可簡化為:

(4)

2.1.1 控制器設(shè)計

采用滑模控制器[7-10],定義位置誤差:

(5)

設(shè)計非奇異終端滑模[12,14]函數(shù):

(6)

其中,cij>0,1ai2,(i=x,y,z;j=1,2,3).為了減弱抖震現(xiàn)象,采用連續(xù)的趨近率[15]函數(shù):

(7)

(8)

由式(3)得垂直速度控制量U1:

(9)

2.1.2 自適應(yīng)RBF神經(jīng)網(wǎng)絡(luò)

RBF神經(jīng)網(wǎng)絡(luò)模擬了生物神經(jīng)系統(tǒng)對信號進行調(diào)整、覆蓋、接受,是一種并行式網(wǎng)絡(luò)結(jié)構(gòu).其結(jié)構(gòu)簡單、計算量小、學(xué)習(xí)速度快并且可逼近任何非線性函數(shù).在非奇異終端滑模控制器中引入由RBF神經(jīng)網(wǎng)絡(luò)預(yù)測未知干擾,可增強系統(tǒng)魯棒性的同時有效減弱控制器的抖震現(xiàn)象.

以X方向的擾動fx預(yù)測為例,RBF神經(jīng)網(wǎng)絡(luò)共3層結(jié)構(gòu),分別是輸入層、隱含層和輸出層,其中隱含層的神經(jīng)元激活函數(shù)由高斯基函數(shù)構(gòu)成,輸出層由隱含層加權(quán)求和得到.文本采用2-5-1的網(wǎng)絡(luò)結(jié)構(gòu)的RBF神經(jīng)網(wǎng)絡(luò),即2個輸入層節(jié)點、5個隱含層節(jié)點和1個輸出層節(jié)點,網(wǎng)絡(luò)結(jié)構(gòu)圖如圖3所示.

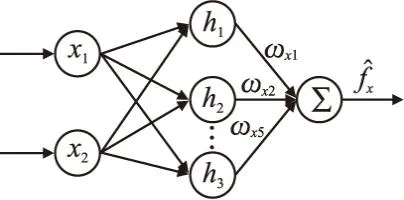
圖3 2-5-1RBF網(wǎng)絡(luò)結(jié)構(gòu)圖Fig.3 2-5-1 RBF network structure diagram

(10)

(11)

(12)

2.1.3 系統(tǒng)穩(wěn)定性分析

以X方向的子系統(tǒng)為例,對控制器的穩(wěn)定性進行證明,Y、Z方向與之同理.

1)系統(tǒng)狀態(tài)有限時間到達滑模面

由式(4)～式(6)、式(8)得:

(13)

假設(shè):

fx=WxThx

(14)

其中,Wx是理想權(quán)值.由式(11)～式(14)得:

(15)

采用李雅普諾夫函數(shù)法來證明系統(tǒng)的穩(wěn)定性[17],定義Lyapunov函數(shù):

(16)

其中,βx>0.則:

(17)

將式(15)代入式(17)得:

(18)

為保證系統(tǒng)的穩(wěn)定性,取自適應(yīng)律為:

(19)

由于sa1sat(sa1)≥0,將式(19)帶入式(18)可得:

(20)

因此,sx有限時間收斂到0.

2)誤差有限時間收斂

當t=t1時,系統(tǒng)狀態(tài)到達滑模面,由式(6)得:

(21)

(22)

對式(22)兩邊積分得:

(23)

設(shè)t=t2時,ex(t2)=0,那么:

(24)

由此可知,誤差可在有限時間收斂到零.

2.2 姿態(tài)控制器設(shè)計

限制姿態(tài)角的波動幅值,可有效提升四旋翼飛行的穩(wěn)定性.因此,根據(jù)姿態(tài)角解算結(jié)果的不同,本文設(shè)計了3種控制模式.

模式1.對偏航角設(shè)置期望值跟蹤,求解滾轉(zhuǎn)角與俯仰角的期望值并進行跟蹤;

模式2.對俯仰角設(shè)期望值跟蹤,求解滾轉(zhuǎn)角與偏航角的期望值并進行跟蹤;

模式3.對滾轉(zhuǎn)角設(shè)期望值跟蹤,求解偏航角與俯仰角的期望值并進行跟蹤.

首先,設(shè)定飛行器的滾轉(zhuǎn)角與俯仰角的安全區(qū)間(-σ,σ),σ>0,當初步求解得到的期望滾轉(zhuǎn)角和期望俯仰角均未超出安全區(qū)間時,采用模式1控制;當初步求解出的期望滾轉(zhuǎn)角或期望俯仰角超出安全區(qū)間時,對超出安全區(qū)間的期望姿態(tài)角度設(shè)置固定期望值為邊界值σ(-σ),并重新解算其余兩姿態(tài)角度的期望值;當初步求解得到的期望滾轉(zhuǎn)角和俯仰角均超出安全區(qū)間時,對超出更多的姿態(tài)角度設(shè)置固定期望值為邊界σ(-σ),并重新解算其余兩期望姿態(tài)角度的期望值;對俯仰角設(shè)置固定期望值時采用模式2控制,對滾轉(zhuǎn)角設(shè)置固定期望值時采用模式3控制.

2.2.1 期望姿態(tài)角度求解

由式(4)得:

(25)

由于:

(26)

因此由式(25)、式(26)聯(lián)合可得到:

(27)

將U1=muz/(cosφd1cosθd1)代入式(27)可以反解得:

(28)

由此,可根據(jù)位置控制器輸出ux、uy、uz和任意一姿態(tài)角的期望值解算得到其余兩個姿態(tài)角的期望值.

1)模式1姿態(tài)解算

根據(jù)跟蹤軌跡預(yù)設(shè)的偏航角初步期望值ψd0求解滾轉(zhuǎn)角與仰俯角的初步期望值θd0與φd0,由式(28)可得:

(29)

由式(29)可以看出,可根據(jù)位置控制器輸出ux、uy、uz和任意一個姿態(tài)角的期望值解算得到其余2個姿態(tài)角的期望值.

當θd0與φd0均在所設(shè)的安全區(qū)間內(nèi)時,期望姿態(tài)角度:

(30)

2)模式2姿態(tài)解算

對俯仰角設(shè)置期望值θd,求解滾轉(zhuǎn)角與偏航角的期望值,由式(28)可得:

(31)

則:

(32)

其中:

(33)

令:

(34)

對X進行限幅,當X>1時,取X=1;當X<-1時,取X=-1.由ψd1、ψd2與當前偏航角ψ的差的絕對值來取舍所得解,即:

(35)

由式(28)、式(35)得:

(36)

3)模式3姿態(tài)解算

對滾轉(zhuǎn)角設(shè)期望值φd,求解俯仰角與偏航角的期望值,由式(28)得:

(37)

其中:

(38)

與模式2同理,先對式(37)的反正弦函數(shù)的括號內(nèi)部限幅后,再由ψd1、ψd2、ψd3、ψd4與當前偏航角ψ的差的絕對值來取舍所得解,即:

(39)

其中i=1,2,3,4.由式(28)、式(39)得:

(40)

2.2.2 控制器設(shè)計

定義姿態(tài)誤差為:

(41)

設(shè)計非奇異終端滑模函數(shù):

(42)

超螺旋算法是二階滑模控制中的一種特殊的算法[11].由于其算法結(jié)構(gòu)簡單需要參數(shù)少且可以抑制滑模控制的抖震現(xiàn)象,有利于提升四旋翼的飛行姿態(tài)穩(wěn)定性.因此,采用超螺旋控制率[6],控制量U2為:

(43)

其中,kφ1、kφ2、kφ3均為正常數(shù).同理可得控制量U3、U4.

3 仿真研究

采用Matlab/Simulink進行四旋翼軌跡跟蹤仿真實驗,運行環(huán)境為Matlab2019a.控制目標是使四旋翼飛行器跟蹤設(shè)定軌跡,控制策略分別采用滑模控制策略(SMC)、外環(huán)加入RBF神經(jīng)網(wǎng)絡(luò)的單模式滑模控制策略(RBF-SMC)、在RBF-SMC基礎(chǔ)上加入多模式控制的控制策略(3M-RBF-SMC),如表1所示.

表1 對比方法Table 1 Comparison method

實驗中,引入如式(44)所示的空氣阻力干擾代替四旋翼受到的實際擾動:

(44)

其中,Vx、Vy、Vz為飛行器X、Y、Z方向的速度;k為阻力系數(shù),k=5.為驗證控制策略的有效性,3種控制策略的控制器采用相同的參數(shù)設(shè)置.仿真實驗中參數(shù)設(shè)置如下:四旋翼模型參數(shù):m=2kg、g=9.8m/s2、Ix=Iy=0.001kg·m2、Iz=0.002kg·m2;位置控制器參數(shù):cx1=cy1=cz1=1、cx2=cy2=cz2=0.1、cx3=cy3=cz3=1、ax1=ay1=az1=3、ax2=ay2=az2=1.5、ηx=ηy=ηz=5、kx=ky=kz=3;RBF神經(jīng)網(wǎng)絡(luò)參數(shù):bx=by=bz=[5,5,5,5,5]、Cx=Cy=Cz=[-1,-0.5,0,0.5,1;-1,-0.5,0,0.5,1]、βx=βy=βz=2;姿態(tài)控制器參數(shù):σ=0.5,cφ1=cθ1=cψ1=1、cφ2=cθ2=cψ2=70、cφ3=cθ3=cψ3=1、aφ1=aθ1=aψ1=3、aφ2=aθ2=aψ2=1.5、kφ1=kθ1=kψ1=100、kφ2=kθ2=kψ2=10、kφ3=kθ3=kψ3=0.25;仿真步長設(shè)置為0.01s;四旋翼初始位置為(0,0,0),初始姿態(tài)為(0,0,π/6),跟蹤的軌跡為使用分段函數(shù)設(shè)計的折線.仿真結(jié)果如圖4～圖6所示.

圖4 擾動預(yù)測曲線Fig.4 Disturbance prediction curve

圖4為RBF神經(jīng)網(wǎng)絡(luò)對未知擾動的預(yù)測曲線,可以看出,RBF神經(jīng)網(wǎng)絡(luò)可以對未知擾動有著較為準確的預(yù)測.圖5為軌跡跟蹤曲線,可以看出,在運動過程中,采用未加入RBF神經(jīng)網(wǎng)絡(luò)的SMC控制策略跟蹤效果較最差,存在明顯的誤差,說明加入神經(jīng)網(wǎng)絡(luò)可以明顯提高系統(tǒng)的魯棒性;通過對比RBF-SMC控制策略與3M-RBF-SMC控制策略的軌跡跟蹤曲線,可以發(fā)現(xiàn),在轉(zhuǎn)角處采用3M-RBF-SMC控制策略的軌跡跟蹤誤差會略大于采用RBF-SMC控制策略的軌跡跟蹤誤差,產(chǎn)生該現(xiàn)象的原因是3M-RBF-SMC控制策略在期望滾轉(zhuǎn)角或期望俯仰角過大時重新解算姿態(tài)角度,滾轉(zhuǎn)角與俯仰角的范圍受到限制,導(dǎo)致轉(zhuǎn)彎時軌跡跟蹤精度降低.圖6為RBF-SMC控制策略與3M-RBF-SMC控制策略的姿態(tài)曲線,可以看出,與RBF-SMC控制策略相比,采用3M-RBF-SMC控制策略會使偏航角有小范圍的波動,但可以明顯降低了滾轉(zhuǎn)角與俯仰角的峰值,使飛行器更加安全穩(wěn)定.因此,3M-RBF-SMC控制策略以跟蹤精度的較少犧牲換取了四旋翼飛行穩(wěn)定性的提升.

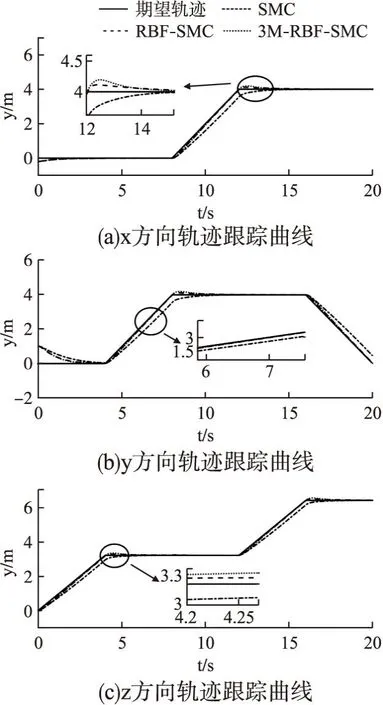
圖5 軌跡跟蹤曲線Fig.5 Trajectory tracking curve

圖6 姿態(tài)角度曲線Fig.6 Attitude angle curve

4 結(jié) 論

本文針對四旋翼飛行器姿態(tài)的穩(wěn)定問題,提出了一種多模式控制的滑模控制器.外環(huán)位置控制子系統(tǒng)采用自適應(yīng)RBF神經(jīng)網(wǎng)絡(luò)對未知擾動進行預(yù)測,并采用非奇異終端滑模控制器實現(xiàn)位置控制和對未知擾動的補償,有效提高了系統(tǒng)的魯棒性.內(nèi)環(huán)姿態(tài)控制子系統(tǒng)采用具備3種姿態(tài)解算模式的超螺旋非奇異終端滑模控制器,使姿態(tài)角保持安全區(qū)間內(nèi),使飛行器更加穩(wěn)定和安全,并通過仿真實驗,驗證了本文所設(shè)計的控制策略的有效性.