一道2022年聯賽試題的探究及在高考中的應用

王東海

(安徽省合肥市肥東縣城關中學,安徽 合肥 231600)

直線與圓錐曲線的位置關系問題一直是高考及聯賽的熱點和難點,頗受命題者的青睞.在這類考題的命題中往往都是探求一些特殊結論,這些結論看似特殊,實則往往都具有普遍性.我們在解答考題后要深入拓展到一般情況,還要注意探尋其他圓錐曲線的對偶性質.下面以2022年四川數學聯賽一道圓錐曲線試題的探究為例進行說明.

1 真題呈現

題目(2022年四川預賽第9題)如圖1所示,ABCD是一個矩形,AB=8,BC=4,M,N分別為AB,CD的中點,以某動直線l為折痕將矩形在其下方的部分翻折,使得每次翻折后點M都落在邊CD上,記為點M′,過點M′作M′P垂直于CD交直線l于點P.設點P的軌跡是曲線E.

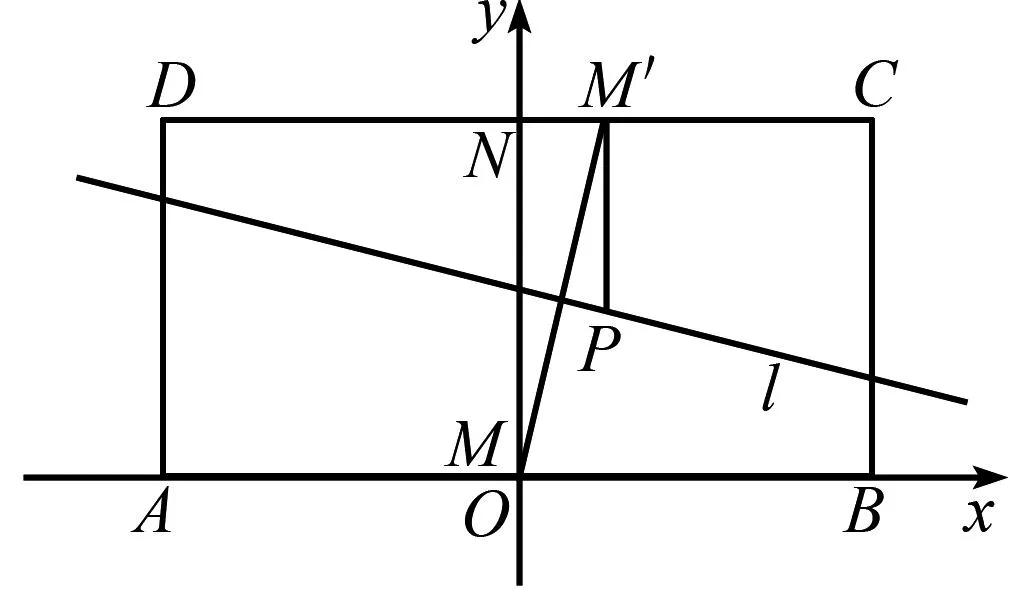
圖1 2022年四川預賽第9題圖

(1)建立恰當的直角坐標系,求曲線E的方程;

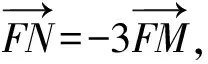
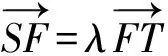
2 解法探究

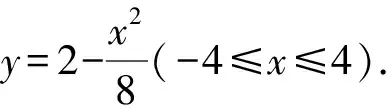
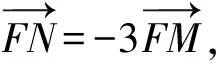
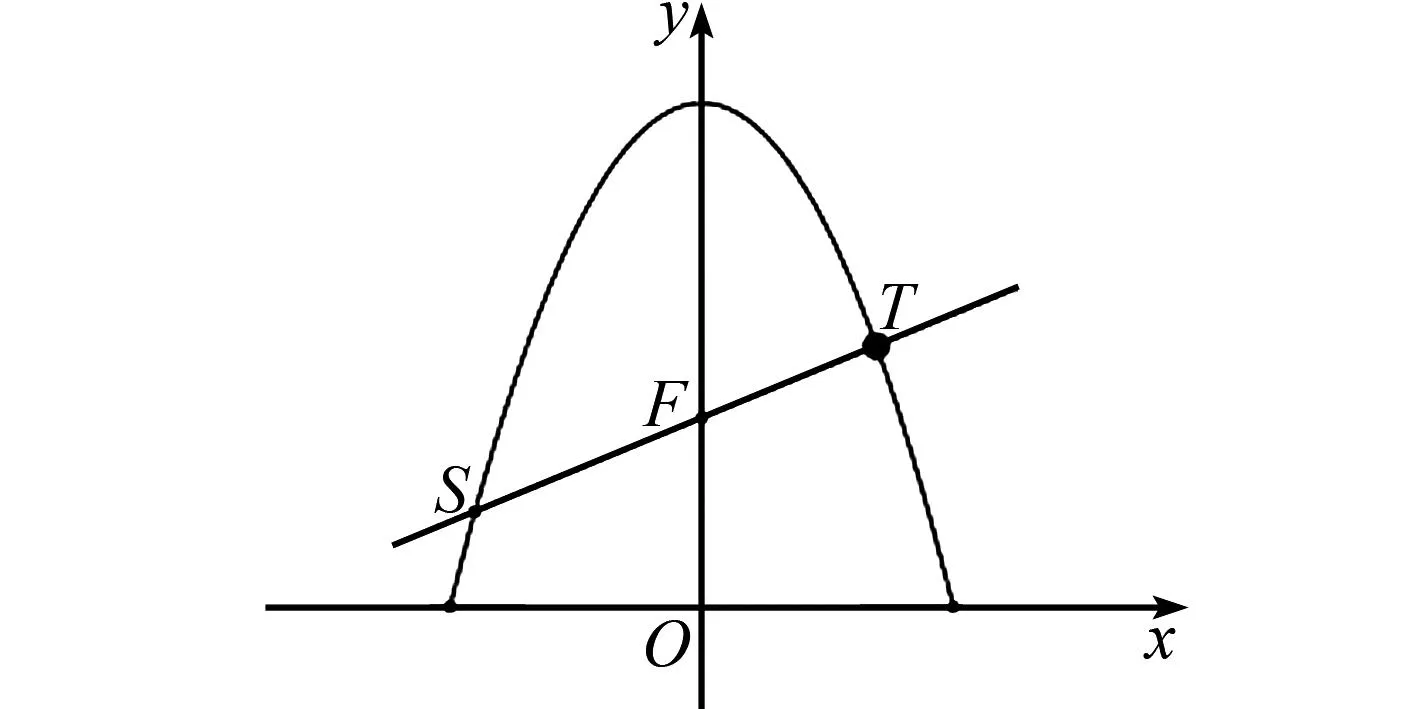
圖2 第(2)小問幾何圖

消元,得x2+8kx-8=0.

①

由韋達定理知x1+x2=-8k,x1x2=-8.

②

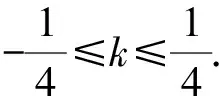
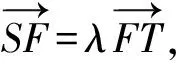
(-x1,1-y1)=λ(x2,y2-1).

所以x1=-λx2.

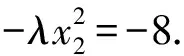
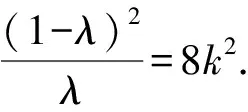
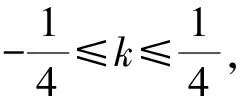
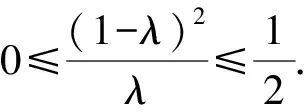
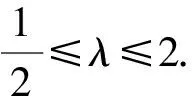
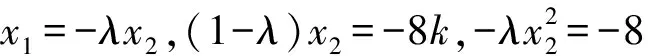
解法2 (點參法)設兩個交點為S(x1,y1),T(x2,y2),因為S,T在拋物線上,有

③

④

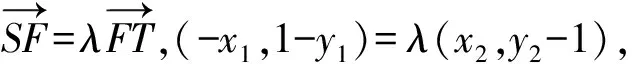
x1=-λx2,y1-1=-λ(y2-1).

將此式代入③,得

再將④式代入,得

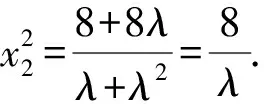
又根據題意知-4≤x2≤4,且由

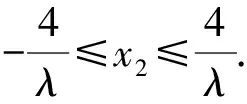
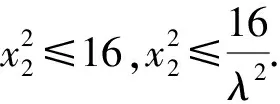
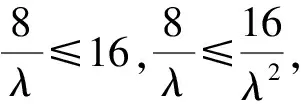
評注首先設出點坐標,然后推出含有五個未知數x1,y1,x2,y2,λ的四個方程,再通過消元處理可以得到x2與λ的一個等式.最后由點T的橫坐標x2的范圍來確定λ的取值范圍.

解法3 (定比點差法)設兩個交點為S(x1,y1),T(x2,y2),因為S,T兩點在拋物線上,有

③

④

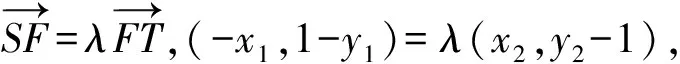
x1=-λx2,y1-1=-λ(y2-1).

④×λ2-③,得

從而λ2y2=1-λ(y2-1)+2λ2-2.

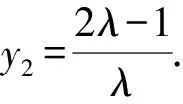
而由題意知0≤y2<2,

⑤

且由0≤y1<2,0≤1-λ(y2-1)<2,

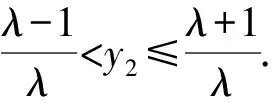
⑥

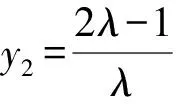
評注先利用定比點差法確定出坐標y2與λ的等量關系,再由坐標y2的范圍定出λ的范圍.使用定比點差法的關鍵在于根據方程特點先配比好系數然后作差,相比解法2運算量少一些.

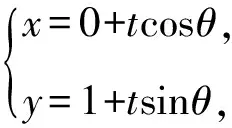
代入拋物線方程,得

整理,得cos2θ·t2+8sinθ·t-8=0.

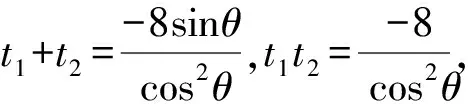
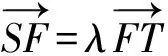
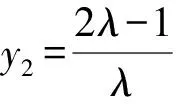
評注對于分點弦這類問題,使用直線的參數方程是常用方法.這是因為t的幾何意義恰能方便表示線段之比問題,但準確理解直線的參數方程中參數的幾何意義是解題的基礎.

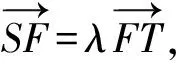
由拋物線參數方程可設T(8t,2-8t2),則得點S(-8λt,1-λ(1-8t2)),

將點S代入拋物線方程,可得

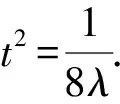
⑦

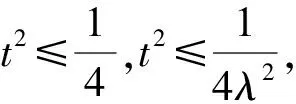
評注利用拋物線參數方程實際上還是先確定t和λ的等量關系,再由坐標t的范圍確定λ的范圍.

3 推廣探究

美籍匈牙利數學家波利亞曾說:“沒有任何一個題目是徹底完成了的,總還會有些事情可以做.”細品解題過程,筆者發現第(2)問的解答值得探究,筆者思考,對于一般性的拋物線有無一個統一的結論呢?需不需要也截取拋物線的一段呢?如果背景的圓錐曲線換成橢圓、雙曲線,是否仍有類似的結論呢[1]?基于以上思考,筆者探究得到如下結論:

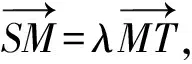
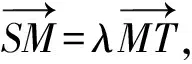
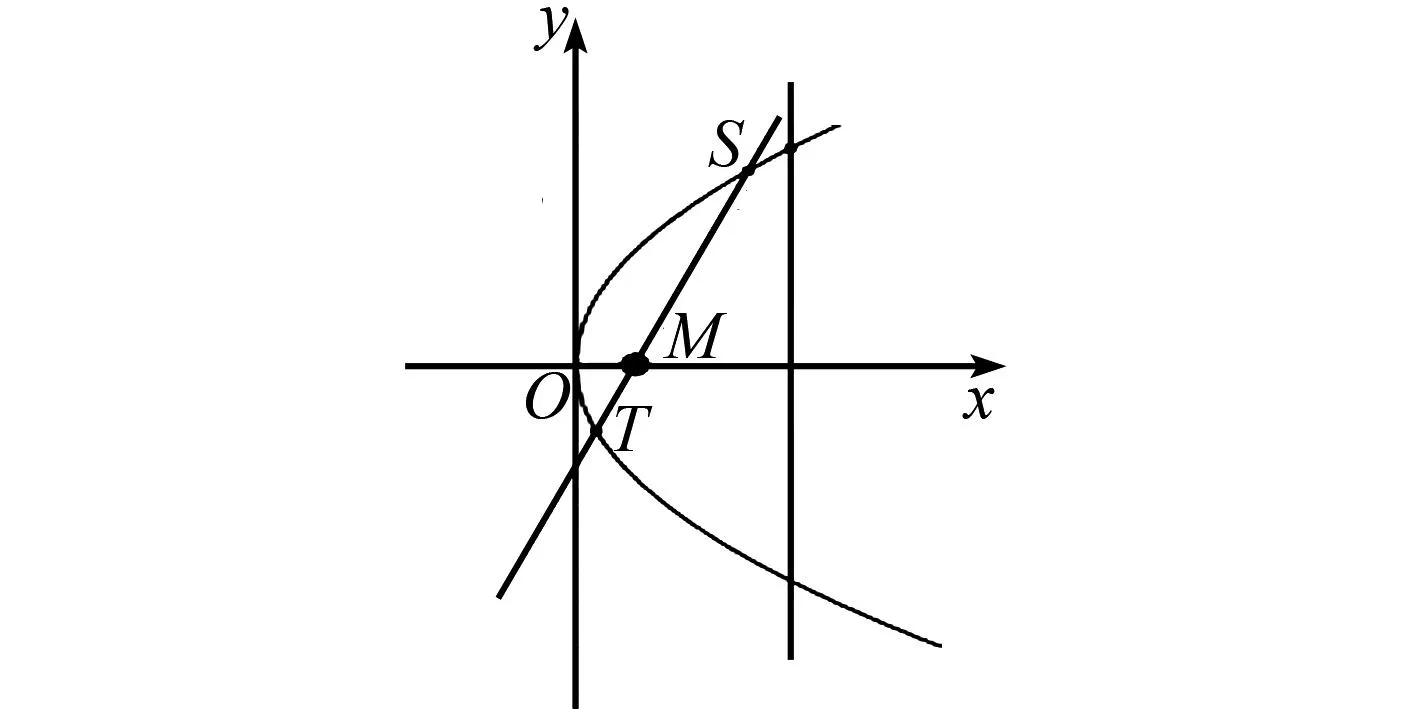
圖3 結論1幾何圖

從而得m-x1=λ(x2-m),-y1=λy2.

所以x1=m-λ(x2-m),

⑧

y1=-λy2.

⑨

又S,T兩點在拋物線上,代入,得

⑩

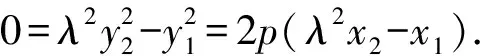
所以λ2x2-x1=0=λ2x2-m+λ(x2-m).

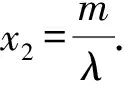
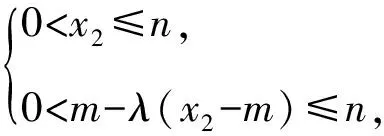
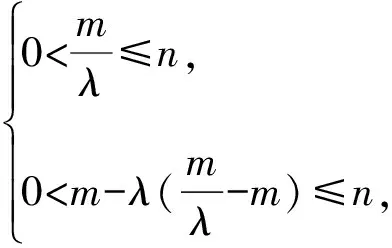
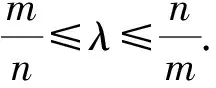
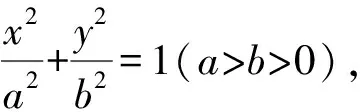
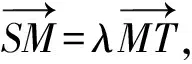
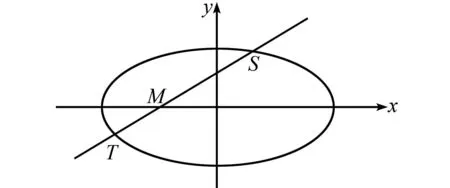
圖4 結論2幾何圖

所以m-x1=λ(x2-m),-y1=λy2.

所以x1=m-λ(x2-m),

⑧

y1=-λy2.

⑨

又S,T兩點在橢圓上,代入,得

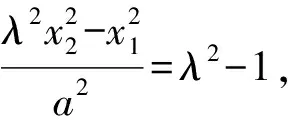
則(x2λ-m-λm+λx2)(x2λ+m+λm-λx2)=(λ2-1)a2.

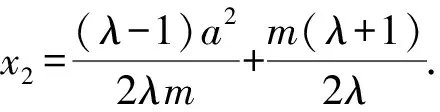
而由題意知-a≤x2≤a.

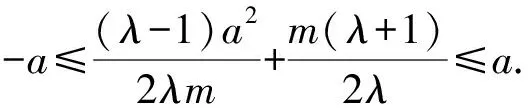
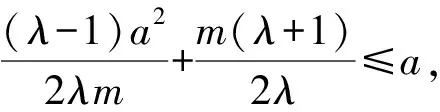
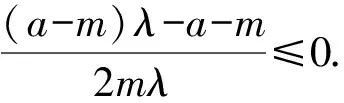
即2mλ[(a-m)λ-a-m]≤0.

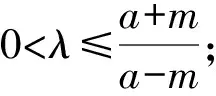
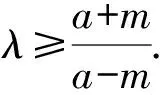
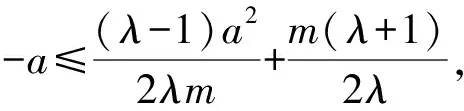
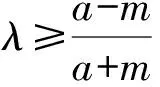
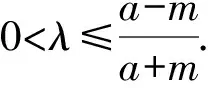
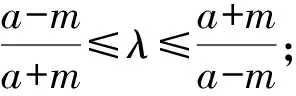
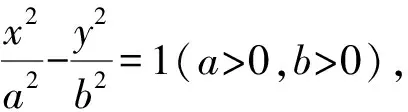
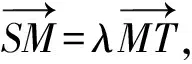
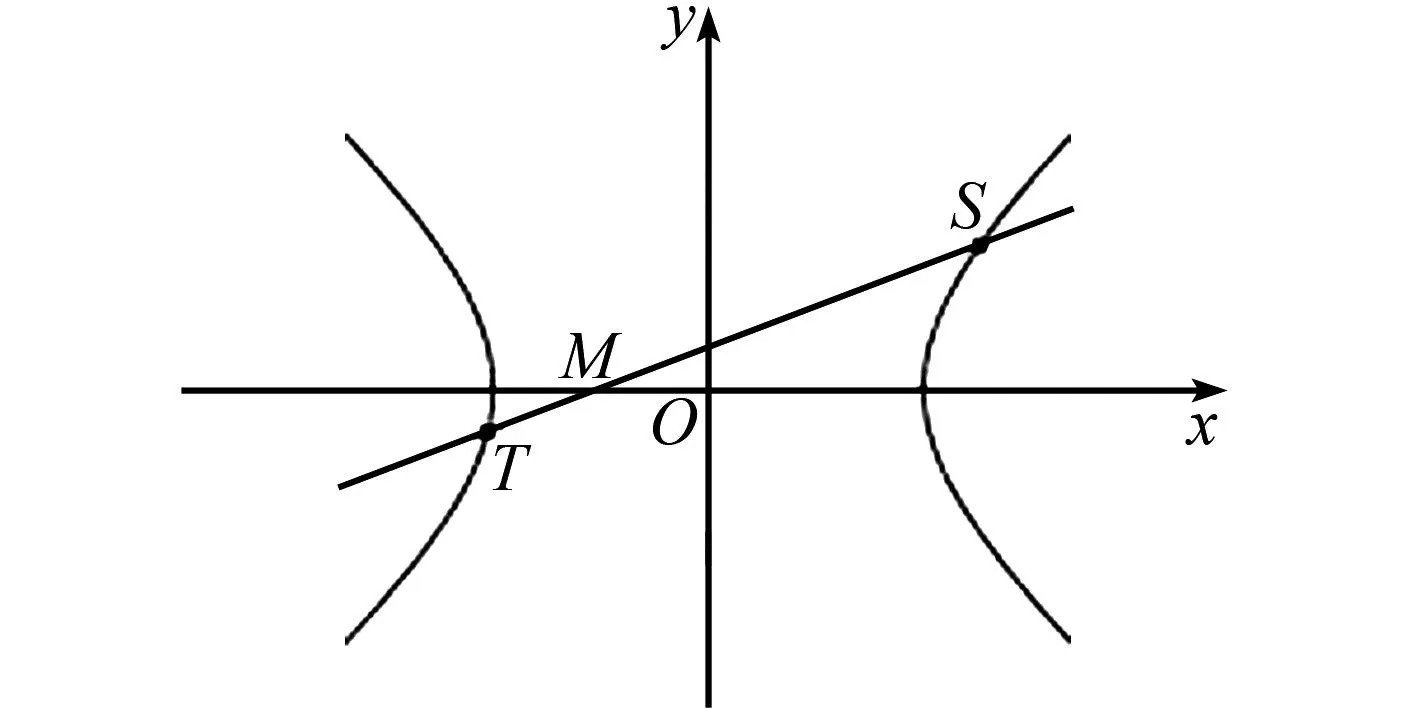
圖5 結論3幾何圖

所以m-x1=λ(x2-m),-y1=λy2.

所以x1=m-λ(x2-m),

⑧

y1=-λy2.

⑨

又S,T兩點在雙曲線上,則有

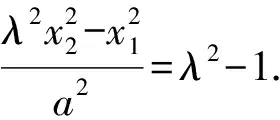
將⑧代入上式,得

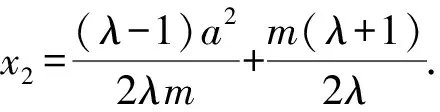
而由題意知x2≤-a,

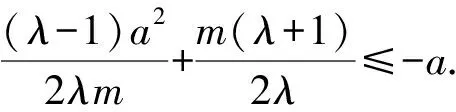
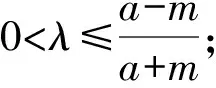
4 變式探究

此道四川聯賽試題,如果我們將題中λ變為常數,而將定點F改為x軸上一個動點(λ,0),那么此動點的橫坐標λ的取值范圍又是怎樣的呢?

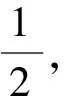
(1)求橢圓Γ的方程;

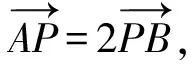
解析(1)易得橢圓Γ:x2+4y2=1.

(2)設A(x1,y1),B(x2,y2),A,B在橢圓上,故

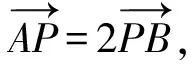
又λ=0不合題意,將式代入,得

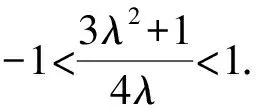
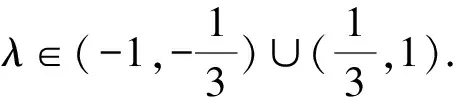
我們根據這道變式題,也可以把它推廣到一般情形 :

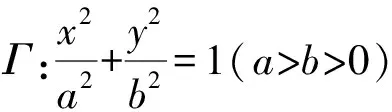
證明方法類似于結論2的定比點差法,略.

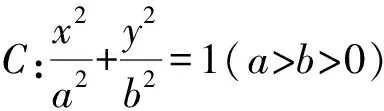
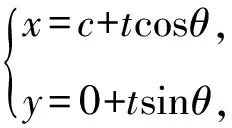
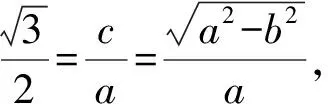
將直線AB參數方程代入橢圓方程x2+4y2=4b2,得(c+tcosθ)2+4t2sin2θ-4b2=0.

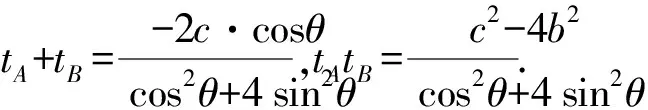
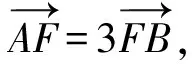
將其代入上式,得

化簡此式可得tan2θ=2.

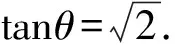
根據這道變式題,可以把它推廣到一般情形:

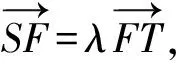
5 結論應用

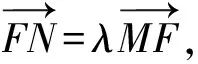
解析設l的縱截距為b,則e=1,k=-b.

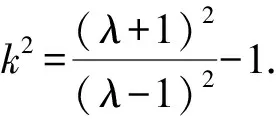
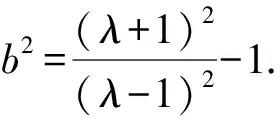
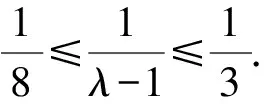
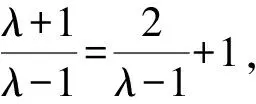
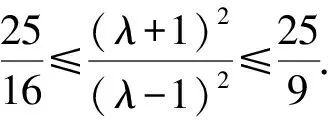
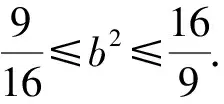
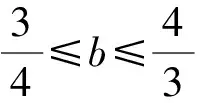
6 結束語

在數學教學中,我們不能滿足于將問題解決了就萬事大吉,而是要進一步進行探究.我們可以進行解法探究,也可以將問題一般化進行拓展研究,還可以進行變式研究.在教學中,教師要為學生提供探究的機會,讓學生在探究中體會到學習的快樂,讓探究成為一種習慣.