基于強化學習的電-氣-熱多微網系統定價策略

李媛，遲昆，王洲，彭婧，賈春蓉，劉炳文

（1.國網甘肅省電力公司經濟技術研究院，蘭州730050；2.西安交通大學電氣工程學院，西安710054）

0 引言

在低碳減排的能源背景下，含電、氣、熱等的多能源微網通過整合多類能源，在提升能源利用效率、滿足用戶靈活多樣的能源需求等方面展現出明顯的優勢［1］。未來電-氣-熱多微網的互聯可形成規模化的電-氣-熱多微網系統。然而由于各類能源的復雜耦合，電-氣-熱多微網系統在規劃、運行與管理等層面面臨諸多挑戰［2］。隨著能源交易市場化，多微網系統可能由微網服務商、微網等諸多市場參與者共同管理。各市場參與者間的交易行為將影響系統的運行和各方的利益［3］。

現有研究已引入了不同的方法研究類似的市場交易。文獻［4］研究了區域綜合能源系統的交易策略，并建立了雙層優化模型。文獻［5］考慮了能源梯級利用以研究能源交易策略。兩者都將雙層模型轉化為單層模型求解。文獻［6-7］等研究使用博弈論來描述市場交易過程。但上述文獻都采用集中式算法求解，考慮到市場環境下參與者之間的競爭與隱私保護行為，集中式算法難以實際應用。

因此，一些研究引入了啟發式等算法以保護用戶隱私。文獻［8］采用了粒子群算法解決配電網與各微網間的斯塔克爾伯格（Stackelberg）博弈。文獻［9］建立了三層優化問題，并采用遺傳算法求解最上層問題。文獻［10-12］等采用類似的啟發式算法優化園區、微網的主從博弈定價策略問題。另外，文獻［13］采用有效集法和最速下降法求解了綜合能源微網交易策略，很好地保護了用戶隱私。然而，對于大規模優化問題啟發式算法難以保證求解效率，得到的可行解可能偏離最優解。有效集法等算法受限于復雜的數學形式，實用性較差。

相對而言，依賴于馬爾可夫決策過程（Markov decision process，MDP）的強化學習算法以求解最優策略為目標，不易陷入局部最優，有更廣泛的適用性。近年來，強化學習特別是深度強化學習（deep reinforcement learning，DRL）算法，在多能系統［14-16］應用廣泛，能更好的應對系統的不確定性［17-18］。文獻［19-20］證明了DRL 算法可兼顧用戶隱私。除文獻［21-22］外少有研究將DRL 算法用于求解類似博弈問題，文獻［21-22］雖將斯塔克爾伯格博弈轉化為MDP，但均未考慮時間耦合約束，然而現實中時間耦合約束是難以忽略的。因此針對所研究的定價問題，本文提出了一種基于強化學習的求解方法，以解決含時間耦合的斯塔克爾伯格博弈問題。

基于以上分析，本文首先描述了電-氣-熱多微網系統內部交易過程并建立了相應的系統模型。其次，微網服務商的定價策略問題被描述為斯塔克爾伯格博弈。可以證明，該博弈存在唯一博弈均衡點。針對這一問題，提出了一種基于強化學習的求解方法以保護用戶隱私并提升求解效率。計算結果表明，該方法有效解決了含時間耦合約束的斯塔克爾伯格博弈問題，制定了符合各方利益的策略。

1 多微網系統模型

1.1 多微網系統結構

本文所研究的電-氣-熱多微網系統如圖1 所示，包含了1 個微網服務商和N個電-氣-熱微網。考慮到微網服務商與各微網均為獨立的經濟實體，交易時各方均追求自身利益最大化。

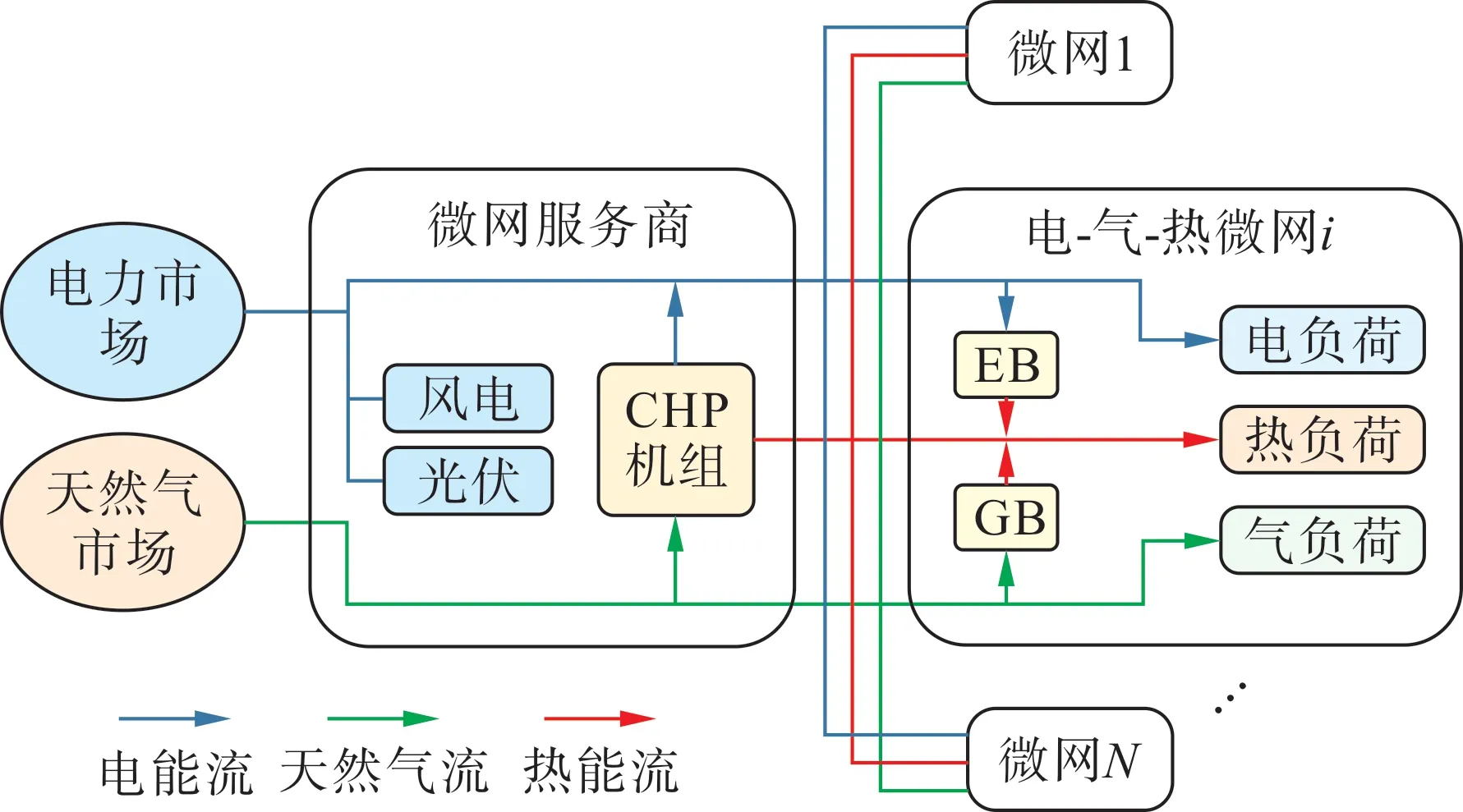
圖1 電-氣-熱多微網系統Fig.1 Electric-gas-heat multi-microgrid system

微網服務商主要服務于配網層面，其向上可接入上級能源市場以購入電能、天然氣，向下可連接區域內多個微網。微網服務商負責區域內配網的建設，其配備風電、光伏和熱電聯產機組等設備用以實現能源整合，同時制定零售價并向各微網供應能源以獲取利潤。

各電-氣-熱微網需從微網服務商購買能源以滿足自身用能需求。各微網均參與綜合需求側響應，根據零售價調整自身策略，同時配備有一定容量的電鍋爐（EB）、燃氣鍋爐（GB）設備以保證更經濟靈活的熱能供應。

本研究假定微網服務商不影響上級能源市場的價格。為保證可再生能源的消納，微網服務商可向上級能源市場出售富余電能，但為避免問題退化，該問題只在多微網系統內部交易完成后考慮。

1.2 微網服務商定價模型

微網服務商首先制定電、氣、熱能零售價，并得到各微網反饋的購能信息。基于所得信息微網服務商進一步優化定價策略和運行策略。

1.2.1 目標函數

微網服務商的目標是最大化其全天凈利潤，如式（1）所示。第一項為售能收入，第二項為總成本，包括購能成本、設備運行成本。

1.2.2 約束條件

多微網系統需滿足各類能源實時供需平衡。如式（2）—（4）所示，等式左側分別表示電、氣、熱能的供應量，等式右側分別表示各能源需求量。

式（5）—（8）為熱電聯產機組的運行約束。式（5）表示機組所消耗標準狀態下天然氣的體積，式（6）表示機組可輸出的電功率限制，式（7）表示機組輸出的熱功率，式（8）為機組的爬坡功率約束。

式中：κa、κb、κc為熱電聯產機組成本系數；λe-h為機組輸出熱、電功率比例；Pchp，max為機組輸出最大電功率；Pchp，rate為機組的最大爬坡速率。

式（9）—（11）為零售價格上下限約束，電、氣、熱能的零售價均應限制在合理范圍內。

1.3 電-氣-熱微網優化模型

各電-氣-熱微網根據能源零售價，進行綜合需求響應，并確定EB和GB的運行策略，以制定最符合自身利益的購能方案。微網模型可統一表示如下。

1.3.1 目標函數

電-氣-熱微網的的目標是最小化全天總成本，如式（12）所示。第一項為從微網服務商購能的成本。第二項包括需求響應成本和靈活供熱成本。

1.3.2 約束條件

EB 設備需滿足功率上下限約束和設備爬坡約束，如式（17）—（18）所示。

同樣地，GB 設備需滿足功率上下限約束和設備爬坡約束，具體形式類比式（17）—（18）。

電-氣-熱微網的實際購能量可由式（19）—（21）確定：

2 斯塔克爾伯格博弈

根據本文所研究的多微網系統模型，微網服務商與各電-氣-熱微網間存在如下交易過程：微網服務商首先向各微網報價；隨后，各微網優化自身策略，以最小化總成本，并將購能量反饋給微網服務商；最后，微網服務商依據反饋結果調整零售價和相關運行變量。此交易模式決定了該定價問題可被描述為“一主多從”結構的斯塔克爾伯格博弈，其中微網服務商可被視為領導者，不同的微網可被視為跟隨者，該博弈包含以下3個部分。

變電站改造期間臨時供電模式的風險及預控措施初探…………………………………………… 李世博，趙紅星（12-81）

1） 競爭者：包括1 個微網服務商和N個電-氣-熱微網，表示為P={MSP，{MG1，…，MGN}}。

可以證明，本文所提出的斯塔克爾伯格博弈存在唯一的博弈均衡點。

在達到博弈均衡點前微網服務商與各微網重復博弈的過程可被視為一類強化學習問題，即智能體代表微網服務商的利益不斷與環境中各微網交互。為此，本文進一步研究了一種基于強化學習的斯塔克爾伯格博弈均衡點求解方法。

3 強化學習求解方法

現有研究將領導者視為智能體（agent），跟隨者視為環境（environment），提出了相應的MDP［20-21］，利用強化學習訓練智能體與環境交互，求解斯塔克爾伯格博弈均衡。但此類方法無法本文模型中存在的式（16）、式（18）等時間耦合約束，這些約束將破壞其MDP 的馬爾可夫性。馬爾可夫性可表示為式（22），是指環境的下一狀態只與當前狀態有關，而與先前狀態無關。

式中：Pr［］表示［］中事件發生的概率。

因此本研究構造了一種新的MDP，以適應存在時間耦合約束的斯塔克爾伯格博弈。包括以下4個元素。

1） 狀態：智能體觀測到的環境狀態。既包括微網服務商已有的信息，如風光機組出力、熱電聯產機組狀態、上級能源市場的購買價格等；也包括各微網反饋的信息。針對某一確定的定價策略，每個微網都有唯一的最優響應，利用這一關系，可用定價策略唯一地表示微網的狀態。因此，狀態向量可表示為式（23）。

式中t包含包括所有僅與時間相關的狀態信息；各類能源的定價策略則反映了各微網的狀態。

3） 回報：智能體的目標應與微網服務商的目標函數一致，即時回報定義為式（25）：

式中：r1為時段1 的即時回報；rt為時段t的即時回報；(at，st)表示微網服務商基于at、st得到的完整定價方案；(s0)表示微網服務商的初始定價方案。

由式（26）可得，智能體總回報為：

4） 狀態轉移：首先，智能體確定某時段的動作值at；隨后，環境根據at確定st中的cet、cgt和cht并計算即時回報rt；最后向智能體反饋st和rt。狀態轉移過程中的st和rt完全取決于at和st-1，馬爾可夫性由式（22）得到保證。

利用該MDP，智能體可逐步優化微網服務商原有的定價策略，從而避免了時間耦合約束對馬爾可夫性的破壞，同時很好地保護了用戶隱私。

基于所提出的MDP，本研究提出的基于強化學習的求解流程如圖2所示。

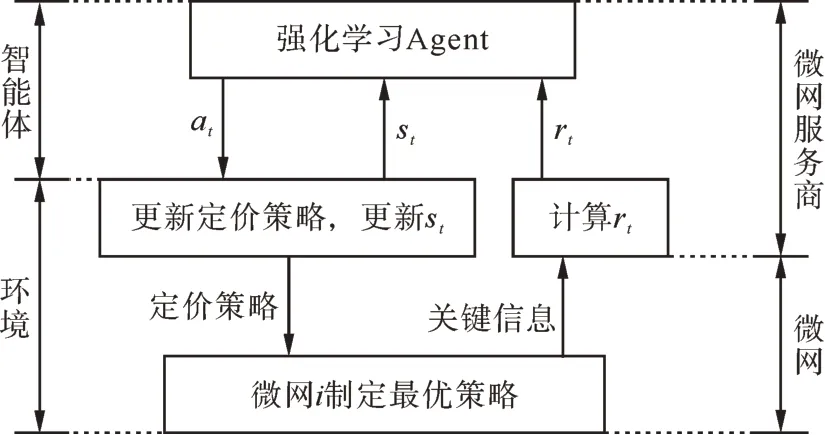
圖2 基于強化學習的求解方法示意圖Fig.2 Schematic diagram of the RL based solution method

4 算例及分析

本文選取了甘肅省3 個電-氣-熱微網作為研究對象。圖3 展示了微網服務商配備的風電、光伏機組的典型出力曲線，圖4 為微網服務商的購能價格，圖5展示了3個微網的典型日負荷曲線。

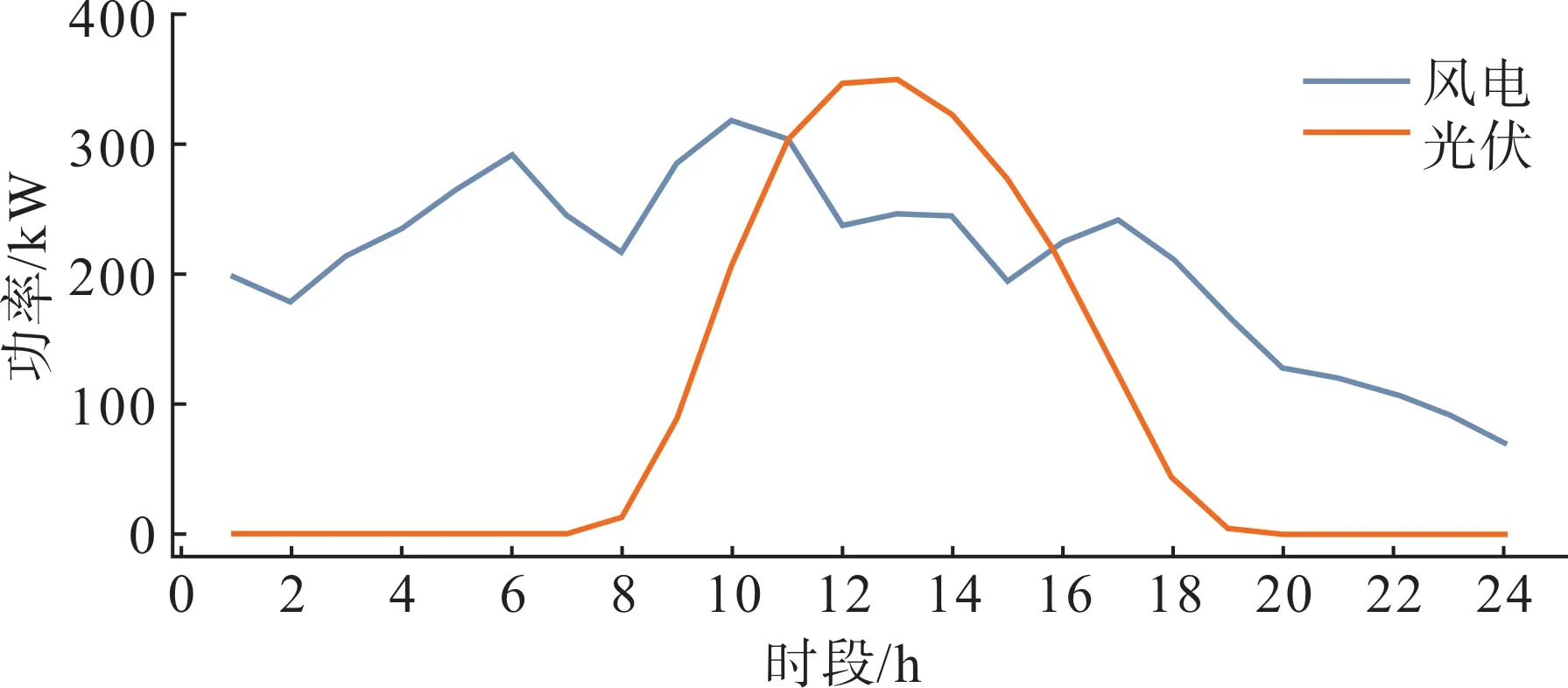
圖3 風電、光伏機組的出力曲線Fig.3 Output power curves of wind turbines and photovoltaic units

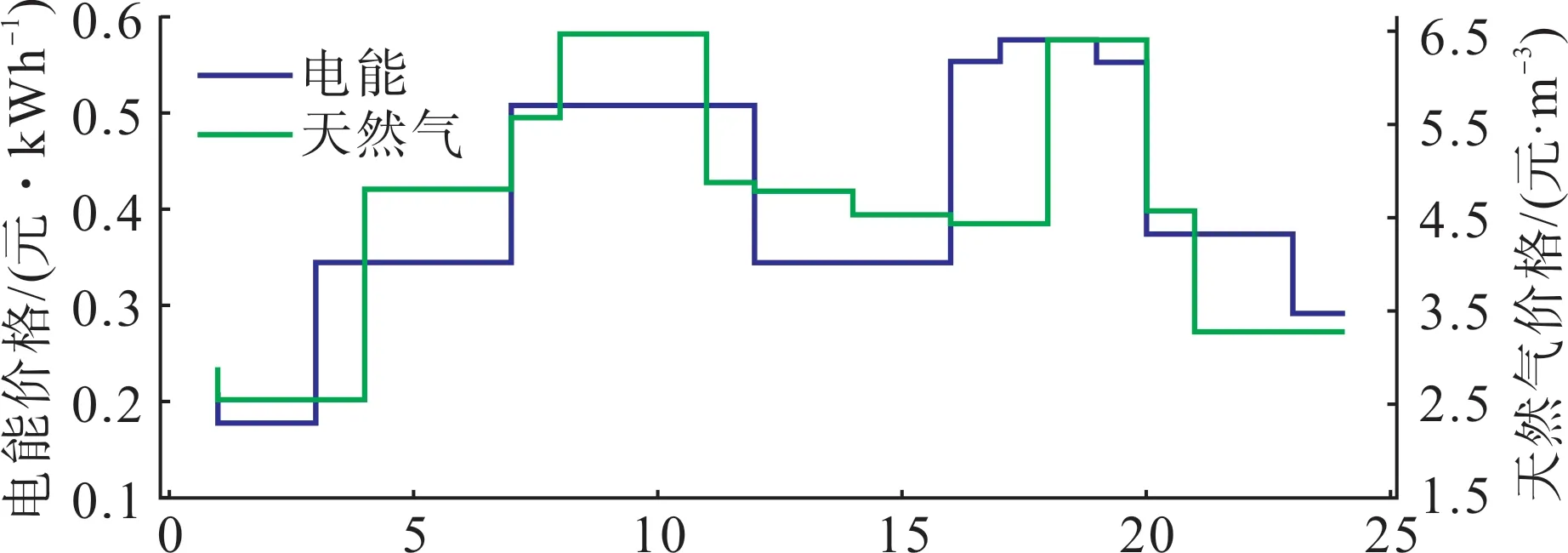
圖4 上級能源市場能源價格Fig.4 Energy prices in superior energy market

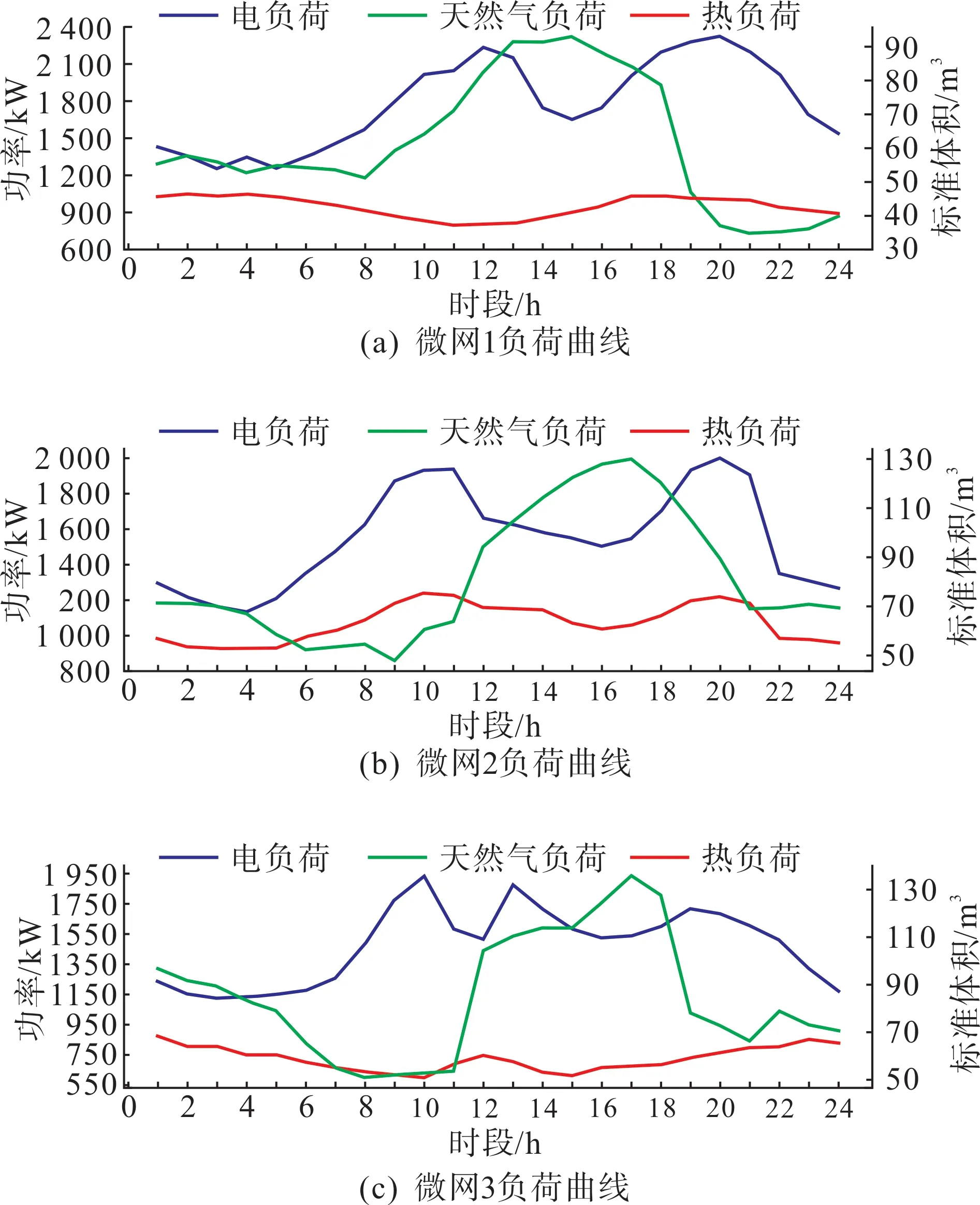
圖5 微網典型日負荷曲線Fig.5 Typical daily load curves of microgrids

電能、天然氣的零售價下限等于上級能源市場價格；熱能的零售價下限以天然氣價格為參照，并考慮一定的制熱成本；各類能源的零售價上限設定為下限的2 倍。微網服務商的初始定價方案設定為各類能源的價格下限。

本文選取了魯棒性強、數據效率高的PPO（proximal policy optimization）算法實現求解。學習率la=4.0×10-4，lc=2.0×10-3；折扣因子γ= 1；梯度裁剪閾值為0.2。

4.1 求解結果

4.1.1 收斂曲線

圖6 展示了本算例的收斂曲線，可以看出求解過程在1 165 次左右收斂。左坐標軸表示智能體的總回報，右坐標軸表示各微網目標函數的負值。訓練初期不合理的定價策略使各微網削減了更多彈性負荷，這使得服務商的利潤較低且微網的需求響應成本較高。隨著訓練的進行服務商的利潤有所提高，更低的需求響應成本也使得微網總成本有所下降。隨著定價策略不斷優化服務商的利潤持續提高，而各微網的總成本也持續增加，圖6 中左右軸對應曲線呈現相反的變化趨勢，這符合斯塔克爾伯格博弈中領導者與跟隨者非合作競爭的利益變化趨勢。當達到博弈均衡時智能體的總回報為43 293.99元，初始利潤為-1 885.81 元，則微網服務商的實際利潤達到41 408.18元，3個微網的總成本分別為43 791.53元、45 718.06元、39 223.76元。

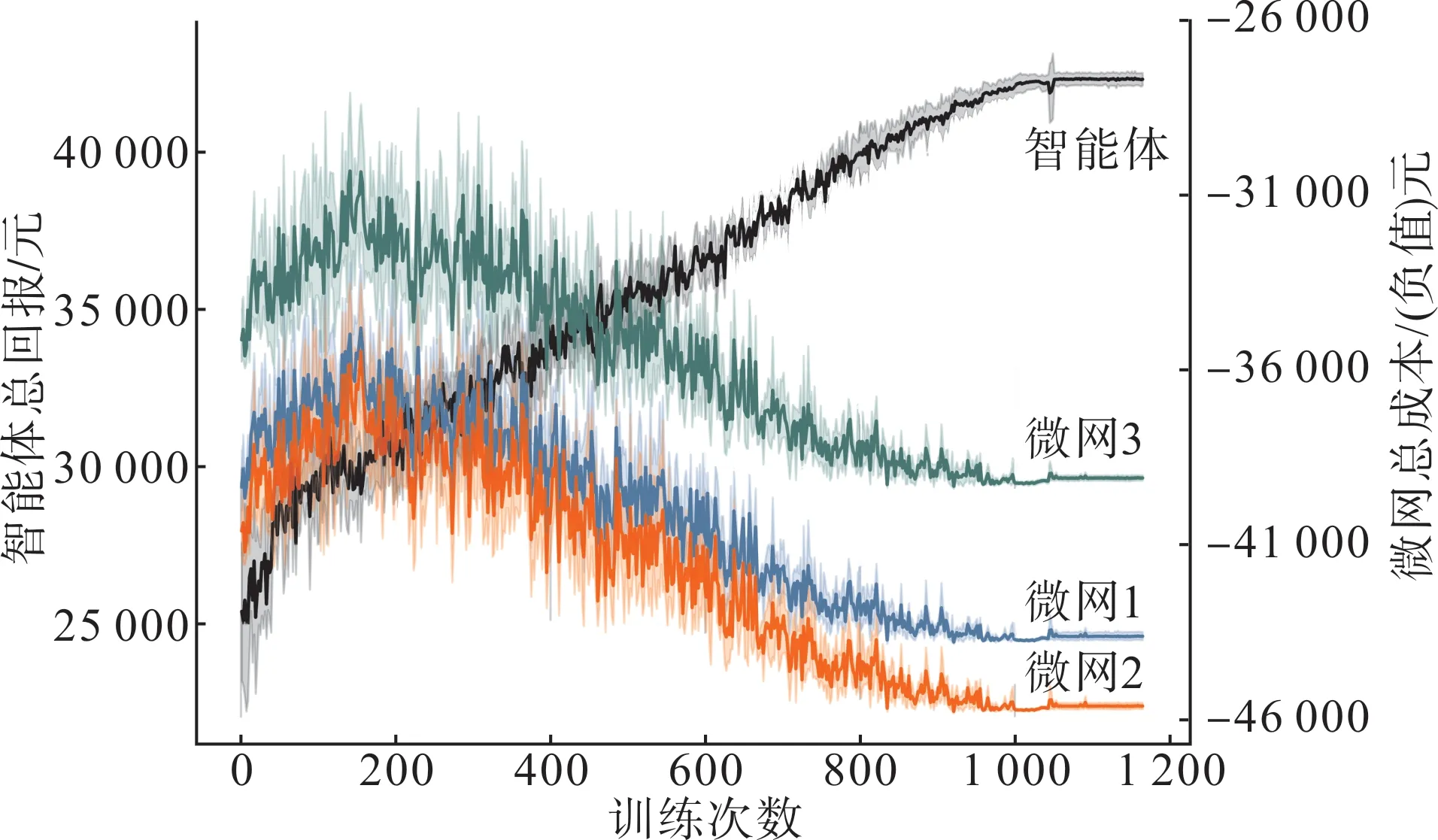
圖6 算例收斂曲線Fig.6 Convergence curves of the case

4.1.2 微網服務商及各微網策略

微網服務商的定價策略如圖7 所示，智能體的動作值 實際為初始定價方案的倍數。受篇幅限制，圖8以微網1為例展示了微網的最優策略。

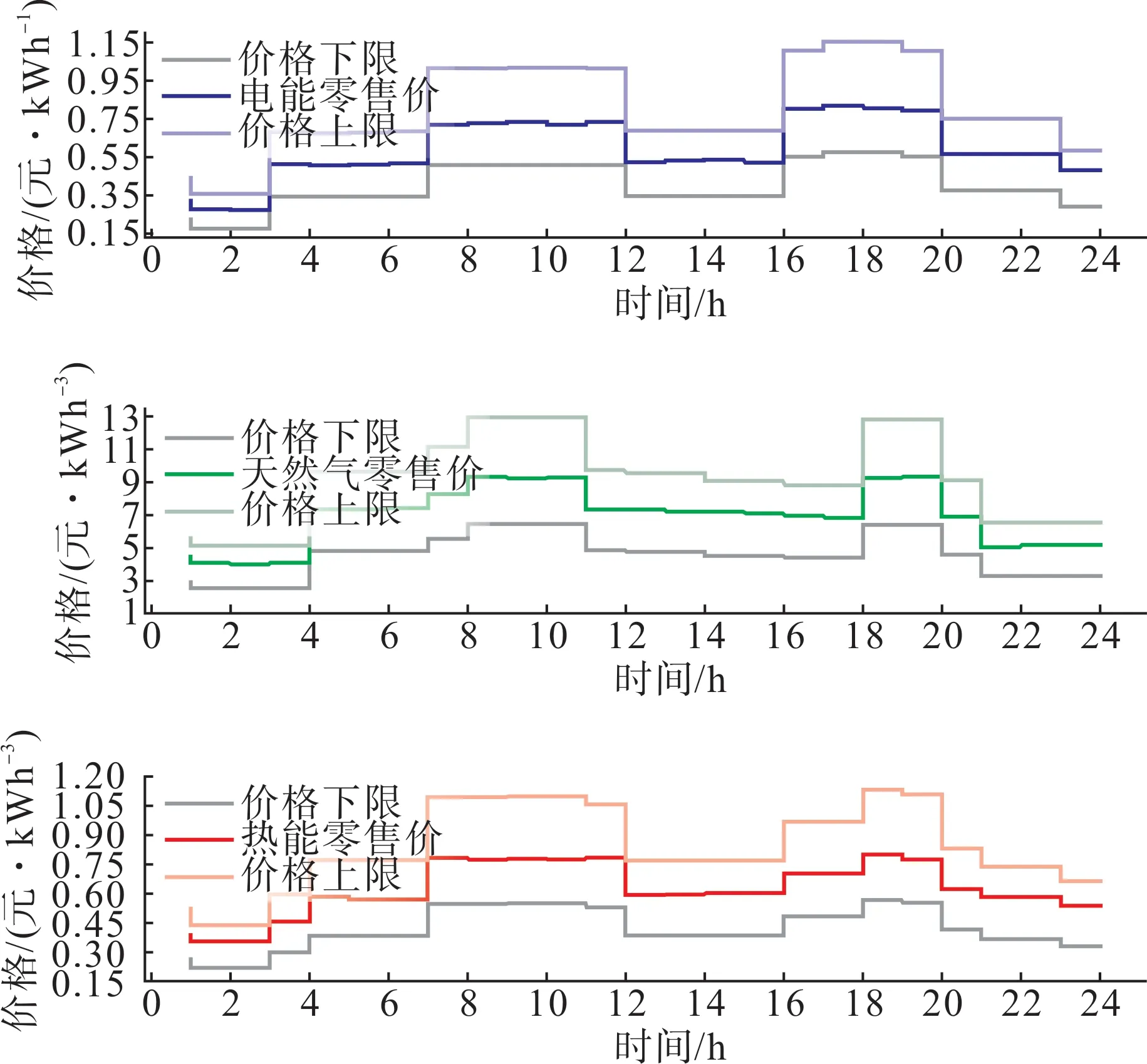
圖7 微網聚合商定價策略Fig.7 Pricing strategy of MSP

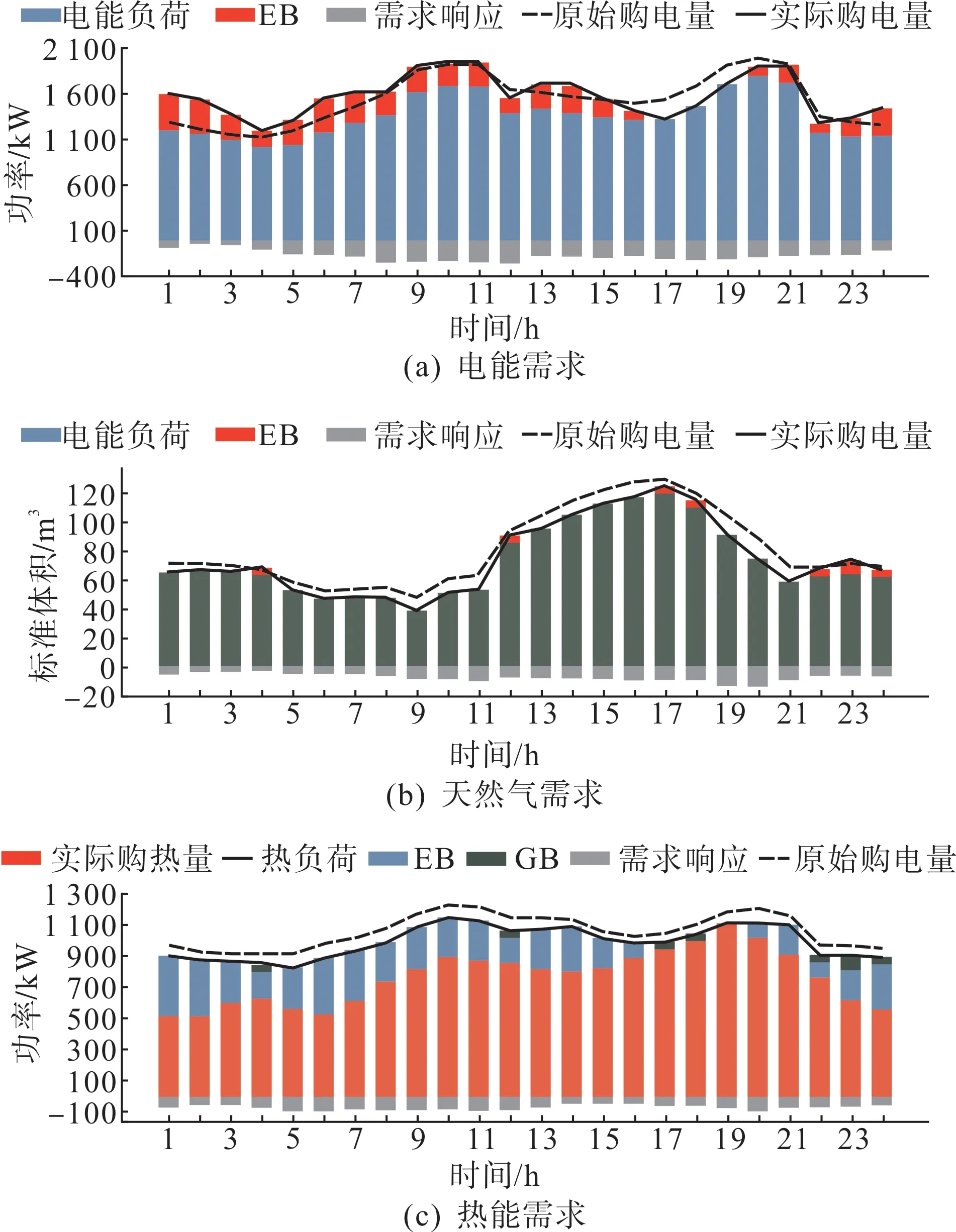
圖8 微網1最優策略Fig.8 Optimal strategy of microgrid 1

可以看出，當價格偏高時各微網會削減或平移更多的彈性負荷以減小購能成本，這也會影響微網服務商的利潤。因此，為避免相應時段的交易量大幅減少，微網服務商會采取更保守的定價策略。對比各微網的策略可以看出，各微網可通過調整需求響應參數影響博弈結果。另外，當熱能零售價過高時各微網也可利用EB、GB降低供熱成本。

4.2 求解方法評估

本節選取了不同的隨機數和零售價價格區間以驗證博弈均衡解的唯一性和所提方法的穩定性。

4.2.1 隨機數

PPO 算法受隨機數的影響，訓練結果可能影響均衡解的結果。圖9 以電價結果為例展示了5 組不同隨機數對均衡解的影響。不同隨機數對交易各方利潤或成本的影響不超過0.83%。

圖9 隨機數對均衡解的影響（以電價為例）Fig.9 Influence of random numbers on the equilibrium solution（e.g.electricity prices）

4.2.2 價格區間

研究不同價格區間，即智能體不同動作空間對結果的影響。圖10以電能零售價為例展示了3種價格區間的求解結果。結果表明不同動作空間下本方法的求解結果穩定。

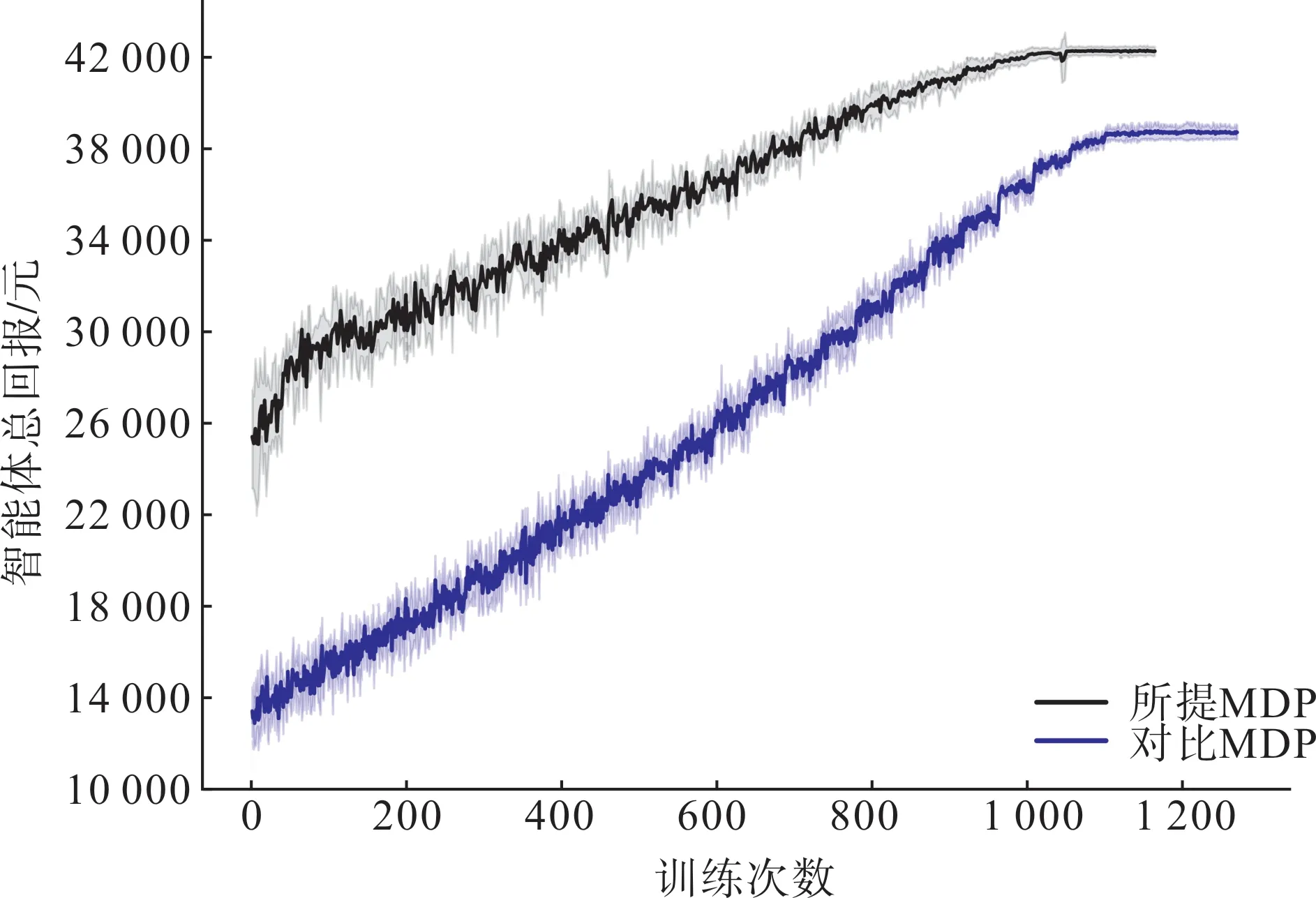
圖11 MDP效果對比Fig.11 MDP effect comparison

4.3 MDP效果對比

本文所提MDP 得到的微網服務商總利潤約為41 408.18 元。根據現有研究的MDP 微網服務商的利潤等于智能體總回報，約為39 525.43 元。由于不滿足馬爾可夫性，對比方法的收斂結果與本文所提MDP 方案差距達到4.55%。另外，由于環境的不確定性對比方法的訓練過程更不穩定。

4.4 計算性能

本節研究了多微網系統中微網數量對計算時間的影響。所有算例在性能相同的計算機上完成求解，計算結果見表1。

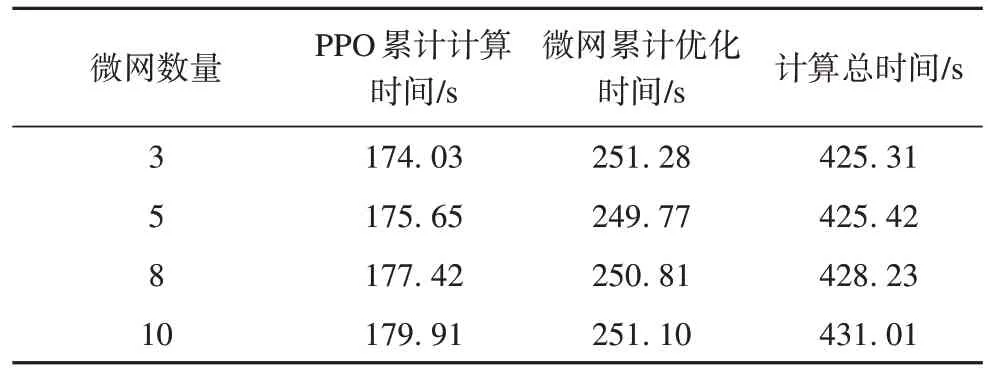
表1 不同微網數量下計算時間Tab.1 Computation time with different numbers of microgrids

本文所提方法展現了良好的計算性能，很好地解決了多微網接入的大規模斯塔克爾伯格博弈問題。由于各微網的優化過程可并行處理，斯塔克爾伯格博弈中跟隨者策略的求解受微網數量的影響較小。同時，微網數量的變化對PPO 算法的訓練時間沒有顯著影響，累計訓練時間僅略有增加。

5 結語

本文研究了電-氣-熱多微網系統中微網服務商零售價定價問題。所建立的多微網系統準確描述了微網服務商與各電-氣-熱微網間的交易模式，所關注的定價問題被描述為斯塔克爾伯格博弈，并被證明存在唯一的博弈均衡點。算例研究表明，所提出的基于強化學習的求解方法能很好地求解存在時間耦合的斯塔克爾伯格博弈。微網服務商采取了恰當的定價方案以提高利潤，各微網也能根據特定參數優化自身策略。此外，該方法很好地保護了各微網的隱私并提升了求解效率。