基于±800 kV特高壓直流輸電線路的中美規(guī)范風荷載對比研究

羅永磊，趙 崢，楊光耀

(中國電力工程顧問集團華東電力設計院有限公司，上海 200063）

0 引言

中美規(guī)范在輸電線路桿塔的荷載設計差異性大，在美國規(guī)范被高度驗證和認可的背景下，研究兩者應用的差異：一方面有助于中國規(guī)范在國際工程的理解、應用和推廣，另一方面在±800 kV特高壓直流輸電線路的電壓等級、單體規(guī)模相比常規(guī)線路工程不同，形成了一系列差異化設計。

風荷載通常是影響架空輸電線路結(jié)構(gòu)的主要因素，雖然美國規(guī)范和中國規(guī)范都是基于Davenport風速譜，但美國規(guī)范[1]主要通過調(diào)整重現(xiàn)期(mean recurrence intervals，MRI)來提升結(jié)構(gòu)可靠性，而中國規(guī)范[2]主要通過結(jié)構(gòu)重要性系數(shù)、分項系數(shù)調(diào)整風荷載效應以保證結(jié)構(gòu)可靠度。因此，從設計值進行分析能更清楚反映兩者的水平差別。

1 極限狀態(tài)設計法研究

1.1 重要性系數(shù)

中國規(guī)范規(guī)定建筑結(jié)構(gòu)設計時要根據(jù)結(jié)構(gòu)破壞可能產(chǎn)生的后果(危及人的生命、造成經(jīng)濟損失、產(chǎn)生社會影響等)嚴重性，采用不同的安全等級。將輸電線路劃分為三種結(jié)構(gòu)安全等級，分別為特高壓工程、110～750 kV線路工程以及臨時線路工程，不同安全級別的安全度設置水平通過結(jié)構(gòu)重要性系數(shù)來反映，特高壓工程的安全等級劃分為一級，重要性系數(shù)通常取為1.1。

相對應的，美國規(guī)范[3]根據(jù)使用條件、重要性及破壞后造成的損失程度，將建筑物分為四類風險類別：結(jié)構(gòu)失效對人的生命風險較低的為Ⅰ類，結(jié)構(gòu)失效可能會對平民日常生活造成重大經(jīng)濟影響或大規(guī)模破壞的為Ⅳ類，結(jié)構(gòu)失效可能對人的生命造成重大風險為Ⅲ類，其余均劃為Ⅱ類。但對于風荷載，各類建筑的重要性系數(shù)均為1.0。

1.2 荷載分項系數(shù)

中國規(guī)范風荷載分項系數(shù)取為1.4，而美國規(guī)范自2016年修整后將風荷載分項系數(shù)由1.6調(diào)整為1.0，主要通過業(yè)主要求來調(diào)整MRI，以此針對性地提升抗風能力。

1.3 風荷載重現(xiàn)期MRI

中國規(guī)范的風荷載MRI與電壓等級有關，對于±800 kV特高壓直流輸電線路工程，考慮到特高壓線路的重要性，MRI按照100 a考慮，風速值提高約6%，風壓值提高約12%。

美國規(guī)范[3]根據(jù)建(構(gòu))筑物風險級別，對不同風險級別建(構(gòu))筑物的風速取值取不同的MRI，對于風險級別為I、II、III、IV的建筑物MRI分別為300 a、700 a、1 700 a以及3 000 a，而適用于輸電線路的專用標準則要求可采用100 a。

2 風荷載設計分析

2.1 基本風速(風壓)

對于基本風壓的計算，由于統(tǒng)計資料和統(tǒng)計時間較長，美國規(guī)范和中國規(guī)范均根據(jù)氣象臺、站搜集到的歷年最大風速資料，按耿貝爾極值I型概率分布計算得到一定重現(xiàn)期、觀測平均時距和基準高度下的最大風速統(tǒng)計值，即為基本風速。中國規(guī)范對于±800 kV直流特高壓線路的基本風速取空曠平坦地面上10 m高度處10 min時距的平均最大風速，MRI為100 a。而美國規(guī)范對線路的基本風速取空曠平坦地面上10 m高度處3 s時距的陣風風速，MRI同樣為100 a，兩者主要差別在于時距。對于不同時距平均風速的對比關系，美國規(guī)范[1]提供了近似的比值關系，美國規(guī)范與中國規(guī)范對于±800 kV直流特高壓線路的設計風速比值大約為1.43。

2.2 地形地貌和高度影響因素

中美規(guī)范均對地形地貌進行了分類，并在風速(風壓)高度變化系數(shù)中考慮地面粗糙度的影響。體現(xiàn)在計算公式中，都是采用指數(shù)公式來計算風壓高度變化系數(shù)。

式中：zh為距地面高度；zg為常數(shù)；K、α為與地面粗糙類別有關的系數(shù)，參數(shù)對比見表1所列。需要注意的是，中美規(guī)范對于架空輸電線路地面粗糙類別分類不一樣：中國規(guī)范按照B類地面粗糙類別設計，美國規(guī)范按照C類地面粗糙類別設計。

表1 風壓高度變化系數(shù)的計算參數(shù)

將常數(shù)帶入后可知μz/Kz=0.810 7×zh0.09，中美規(guī)范風壓高度變化系數(shù)隨高度的變化關系如圖1所示。

圖1 風壓高度變化系數(shù)對比圖

由圖1可知：1)中國規(guī)范和美國規(guī)范的風壓高度變化系數(shù)均隨距地面高度的增加而增大，高度越高，增加得越慢；2)根據(jù)公式計算，當計算高度大于10.24 m時，中國規(guī)范風壓高度變化系數(shù)與美國規(guī)范相同。隨著高度越高，比值越大，中國規(guī)范與美國規(guī)范比值接近1.07～1.15。

2.3 風載體型系數(shù)

2.3.1 線條和絕緣子串

中國規(guī)范對于線條風載體型系數(shù)μsc，線徑小于17 mm應取1.1，線徑大于或等于17 mm取1.0。±800 kV特高壓線路導線線徑通常均大于17 mm，即導線風載體型系數(shù)μsc取為1.0，地線風載體形系數(shù)μsc取為1.1。而美國規(guī)范線條的風載體型系數(shù)cf取1.0。也就是，中國規(guī)范和美國規(guī)范導線風載體形系數(shù)一致均為1.0，中國規(guī)范地線風載體形系數(shù)1.1大于美國規(guī)范地線風載體形系數(shù)1.0。

2.3.2 桿塔

中國規(guī)范規(guī)定了具體的取值方法：對于角鋼塔為1.3，由角鋼組成四面方形自立式桿塔為1.3(1+η)。其中，η為塔架背風面荷載降低系數(shù)，與填充系數(shù)有關。而美國規(guī)范直接給出了桿塔風載體型系數(shù)(阻力系數(shù))與填充系數(shù)相關的計算公式Cf=4.0φ2-5.9φ+4.0，φ為填充系數(shù)。中美規(guī)范桿塔風載體型系數(shù)，如圖1所示。

由圖2可知：1)中國規(guī)范和美國規(guī)范的結(jié)構(gòu)式桿塔風載體型系數(shù)，均隨著填充系數(shù)的增大而降低；2)當填充系數(shù)大于0.2時，中國規(guī)范與美國規(guī)范比值接近0.7，且基本恒定。

圖2 中美規(guī)范桿塔風載體型系數(shù)

2.4 動力特性

輸電線路為柔性結(jié)構(gòu)，風荷載的脈動性對其影響巨大。中國規(guī)范和美國規(guī)范分別采用風振系數(shù)(線條風可視為陣風系數(shù)βC、檔距折減系數(shù)αL乘積)和陣風響應系數(shù)G來表征輸電線路結(jié)構(gòu)脈動風振。

2.4.1 導地線

中國規(guī)范中，線條的檔距折減系數(shù)αL和陣風系數(shù)βC主要與水平檔距、平均高度相關。當平均高度不變時，水平檔距越大，αL×βC越小。當水平檔距不變時，平均高度越大，αL×βC越小。

美國規(guī)范中，線條的陣風響應系數(shù)Gw也與水平檔距、有效高度相關。當平均高度不變時，水平檔距越大，Gw越小。但是，當水平檔距不變時，平均高度越大，Gw反而越大，結(jié)果見表2所列。

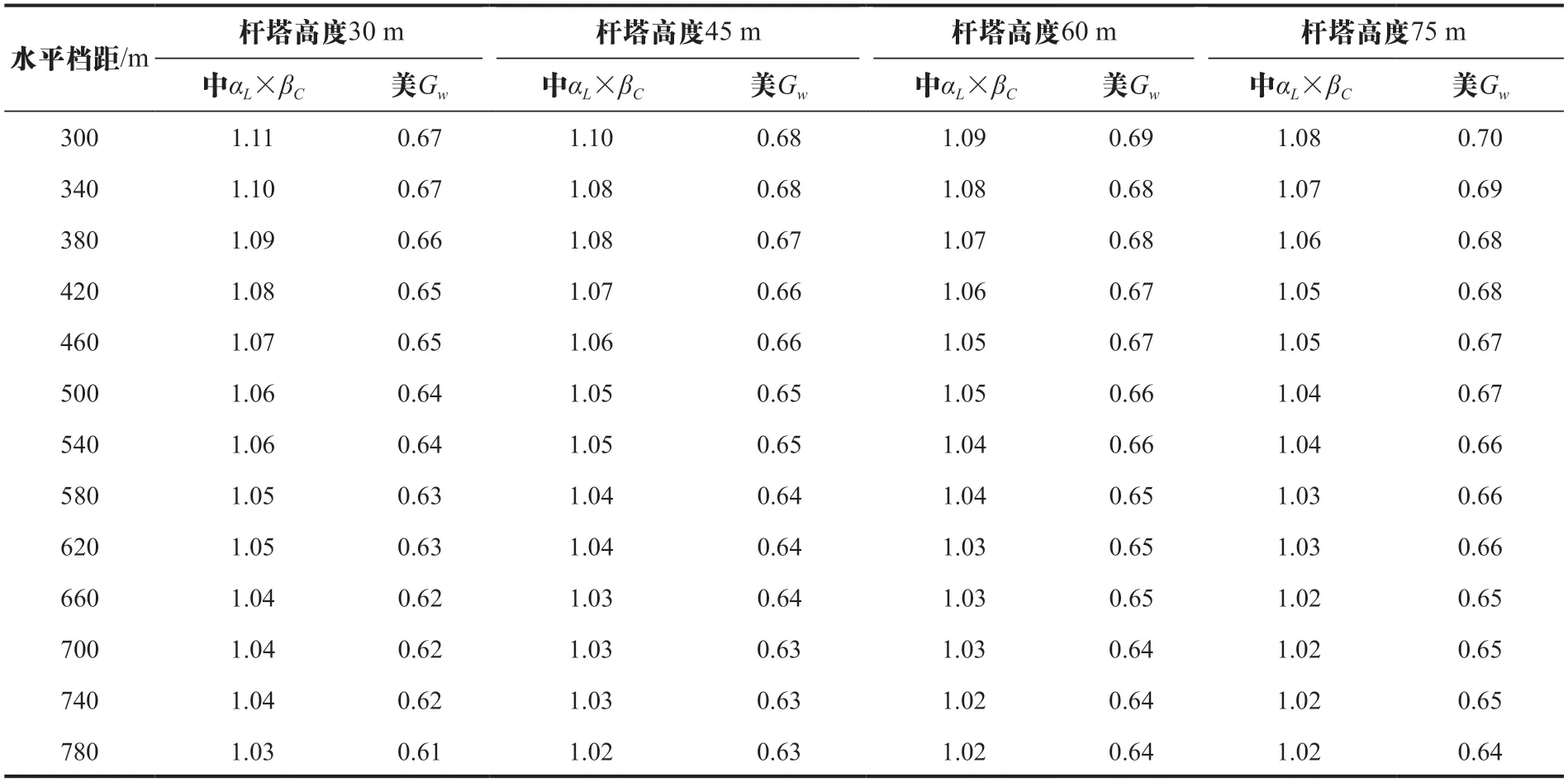
表2 中國規(guī)范αL×βC和美國規(guī)范Gw對比表

中國規(guī)范αL×βC均大于美國規(guī)范Gw，具體比值如圖3所示。

圖3 線條風動態(tài)特性系數(shù)比值(αL×βC/Gw)圖

由圖可知，中國規(guī)范與美國規(guī)范線條風動態(tài)特性系數(shù)比值αL×βC/Gw在1.53～1.67左右，且隨著檔距越大比值越大，導地線高度越大反而比值越小。

2.4.2 桿塔

中國規(guī)范的桿塔風振系數(shù)βZ采用團集質(zhì)量法，將桿塔分段簡化為若干個質(zhì)量和面積等效的點，從而形成基于桿塔外形的“質(zhì)點串”，僅考慮結(jié)構(gòu)第一振型一階自振頻率。其計算值與高度、質(zhì)量、迎風面積、自振頻率等密切相關，因此對于不同桿塔、同一桿塔的不同部分，風振系數(shù)計算值均可能不同。

美國規(guī)范的桿塔陣風響應系數(shù)Gt，則與桿塔計算高度Zh有關，且通常按照全高三分之二的高度作為計算高度，獲得的陣風響應系數(shù)Gt可簡化作為計算全塔的統(tǒng)一值，相對計算簡單。其陣風響應系數(shù)Gt均小于1，基本為0.8～0.84，且均隨桿塔高度的增加而緩慢減小。

中國規(guī)范的桿塔風振系數(shù)βZ大于1.0，體現(xiàn)了動力特性對風荷載的增大效應，而美國規(guī)范的桿塔陣風響應系數(shù)Gt小于1.0，體現(xiàn)了動力特性對風荷載的減小效應。原因主要在于中國規(guī)范采用10 min平均風速，而美國規(guī)范采用3 s的陣風風速。

3 結(jié)構(gòu)風荷載計算分析

以典型30 m/s風速、0 mm覆冰氣象條件的直線角鋼塔為例，單線圖如圖4所示。

圖4 直線塔桿塔單線圖

結(jié)合上文對中美規(guī)范的對比分析，具體設計參數(shù)取值見表3所列。為統(tǒng)一計算水平，將中國規(guī)范10 min平均最大風速換算為美國規(guī)范0.3 s的陣風風速。

表3 設計參數(shù)

3.1 導線風荷載與計算高度

計算高度對導線風荷載的影響主要體現(xiàn)在陣風系數(shù)βC、檔距折減系數(shù)αL(美國規(guī)范陣風響應系數(shù)GW)以及風壓高度變化系數(shù)KZ或μZ，常用經(jīng)濟水平檔距為460 m時，導線風荷載計算結(jié)果如圖5所示。

圖5 不同計算高度的線條風荷載

如圖可知：1)計算高度越高，中國規(guī)范和美國規(guī)范的線條風荷載就越大，基本成線性關系；2)對于線條風荷載標準值，各個高度的中國規(guī)范取值均小于美國規(guī)范，其比值約為0.92且基本恒定；3)對于線條風荷載設計值，受分項系數(shù)、重要性系數(shù)差異影響，趨勢有所變化。各個高度的中國規(guī)范取值均大于美國規(guī)范，其比值約為1.42且基本恒定。

3.2 線條風荷載與水平檔距

水平檔距對線條風荷載的影響主要體現(xiàn)在風振響應系數(shù)GW/風荷載調(diào)整系數(shù)βC，結(jié)合±800 kV架空輸電線路對地距離、實際桿塔排位應用情況，直線塔平均計算高度接近45 m，線條風荷載計算結(jié)果如圖6所示。

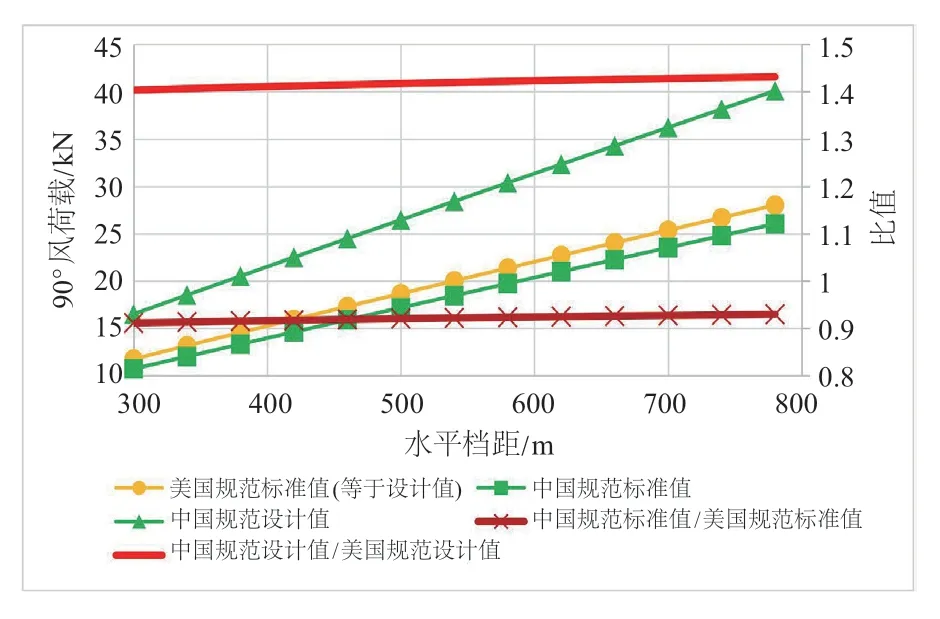
圖6 不同水平檔距的線條風荷載

如圖可知：1)水平檔距越大，中國規(guī)范和美國規(guī)范的線條風荷載就越大，基本成線性關系；2)對于線條風荷載標準值，各個水平檔距的中國規(guī)范取值均小于美國規(guī)范，其比值約為0.92且基本恒定；3)對于線條風荷載設計值，受分項系數(shù)、重要性系數(shù)差異影響，趨勢有所變化。各個水平檔距的中國規(guī)范取值均大于美國規(guī)范，其比值約為1.42且基本恒定。

3.3 塔身風荷載

以Z30101A-66塔型為例，塔身風荷載計算結(jié)果如圖7所示，其中橫擔風荷載僅占塔身風荷載的7%左右，在這里暫不計入。

圖7 Z30101A-66塔身風荷載(各風壓段)

由圖可知：1)對于塔身風荷載標準值，中國規(guī)范取值均小于美國規(guī)范。位置越低，差距越大，在桿塔腿部位置，中國規(guī)范取值與美國規(guī)范的比值約為0.4。隨著高度越高，差距逐漸縮小，當大于60 m時，中國規(guī)范取值與美國規(guī)范基本相等；2)對于塔身風壓設計值，當計算高度小于40 m時，中國規(guī)范取值小于美國規(guī)范，在桿塔腿部位置，中國規(guī)范取值與美國規(guī)范的比值約為0.6。隨著高度越高，差距越小，當計算高度大于40 m時，中國規(guī)范的取值反而大于美國規(guī)范；3)隨著高度增加，中國規(guī)范與美國規(guī)范的塔身風荷載設計值比值由0.6基本線性增加至1.6，這是由于隨著計算高度越高，美國規(guī)范的塔身陣風響應系數(shù)基本不變，而中國規(guī)范的塔身風振系數(shù)基本單調(diào)遞增；4)對于Z30101A-66塔身風荷載總標準值(各風壓段風荷載之和)，中國規(guī)范與美國規(guī)范比值約為0.65，而對于考慮結(jié)構(gòu)重要性系數(shù)以及分項系數(shù)后的設計值，中國規(guī)范與美國規(guī)范比值約為0.99，基本相等。

3.4 典型桿塔整體分析

結(jié)合上述線條和塔身風荷載分析成果，基于Z30101A-66(水平檔距為460 m)典型桿塔，通過中國規(guī)范設計方法進行內(nèi)力分析，從而判斷中美國規(guī)范風荷載對桿塔整體設計影響，輸入條件及計算結(jié)果見表4所列。

表4 Z30101A-66典型桿塔輸入條件及計算結(jié)果 kN

中國規(guī)范線條風荷載設計值為美國規(guī)范的1.41倍，而塔身風荷載基本相當。但是美國規(guī)范高空處計算的風荷載相對較小，而低空處計算的風荷載相對較大，受此塔身風荷載分布特點的影響，使得中國規(guī)范塔身的基礎作用力僅約為美國規(guī)范的1.39倍和1.28倍。

4 結(jié)論

1)美國規(guī)范主要通過調(diào)整MRI來提升結(jié)構(gòu)可靠性，而中國規(guī)范主要通過結(jié)構(gòu)重要性系數(shù)、分項系數(shù)調(diào)整風荷載效應以保證結(jié)構(gòu)可靠度。美國規(guī)范要求常規(guī)桿塔風荷載分項系數(shù)為1.0，MRI為100 a；中國規(guī)范對于±800 kV特高壓線路設計，風荷載分項系數(shù)為1.4，MRI為100 a，重要性系數(shù)為1.1。

2)中國規(guī)范與美國規(guī)范的線條風荷載的比值基本穩(wěn)定，不同高度與水平檔距的影響不大。塔身風荷載由于中國規(guī)范采用團集質(zhì)量法，通過結(jié)構(gòu)振型計算風振系數(shù)，所以塔身風荷載分布差異較大。

3)中國規(guī)范的線條風荷載標準值小于美國規(guī)范，比值基本恒定為0.92左右，但線條風荷載設計值卻大于美國規(guī)范，比值基本恒定為1.42左右。

4)基于Z30101A-66桿塔的分析計算，中國規(guī)范與美國規(guī)范的塔身各風壓段風荷載比值隨著高度增加而增大，設計值比值由0.6線性增加至1.6，這是由于隨著計算高度越高，美國規(guī)范的塔身陣風響應系數(shù)基本不變，而中國規(guī)范的塔身風振系數(shù)基本單調(diào)遞增。即使各分壓段風荷載分布規(guī)律不同，但中國規(guī)范與美國規(guī)范的塔身風荷載總設計值(各風壓段之和)之比約為0.99，基本相等。

5)通過對線條風荷載以及塔身風荷載的綜合分析，對于Z30101A-66典型桿塔的計算，中國規(guī)范的塔身基礎作用力為美國規(guī)范的1.39倍和1.28倍。也就是，按照美國規(guī)范[1]中的《輸電線路設施預標準最小設計荷載草案》來設計±800 kV架空特高壓輸電線路，其風荷載水平低于中國規(guī)范約23%。