環境風載荷下大口徑反射面天線波束指向分析
欒 天, 薛 松,, 連培園,, 余佳恒, 杜雨軒, 王 猛, 趙武林,盧 波, 許 謙, 王從思
(1. 西安電子科技大學 機電工程學院,陜西 西安 710071; 2. 西安電子科技大學 廣州研究院,廣東 廣州 510555;3. 陜西黃河集團有限公司,陜西 西安 710043; 4. 中國電子科技集團有限公司 第三十九研究所,陜西 西安 710065;5. 湖北省鄂州市天元砂輥有限責任公司,湖北 鄂州 436001; 6. 中國科學院 新疆天文臺,新疆 烏魯木齊 830011)
隨著天文學的發展,人類對深空領域的探索不斷深入,要求反射面天線能夠接收來自太空的極為微弱的電磁信號。為了提高觀測性能,反射面天線不斷朝著大口徑、高頻段、高指向的方向發展[1]。隨著反射面天線口徑的不斷增大,其剛度有所降低,環境載荷(如重力、溫度和風等)對反射面天線結構變形的影響逐漸變大。由于重力、溫度均屬于緩變載荷,可通過提前估計其對天線的影響來進行變形補償[2]。但是,風載荷具有時變性、不確定性等特性,如何快速評估風載荷下大口徑反射面天線結構的變形及其對波束指向特性的影響成為研究關鍵[3]。
現階段,國內外學者主要采用2種方法來消除風載荷對大口徑反射面天線變形的影響。第1種方法是安裝天線罩。例如:麻省理工學院的Olmi等[4]為Haystack天文臺的37 m口徑的射電望遠鏡安裝了天線罩,以減小風載荷對天線變形的影響。第2種方法是采用伺服控制系統來調整天線的指向,從而減小風載荷的影響。Kim等[5]將天線視為理想剛體,通過仿真分析驗證了模糊PⅠD(proportional-integral-differential,比例-積分-微分)控制相較于傳統控制方法的優越性。Gawronski[6]針對美國國家航空航天局的深空網絡天線控制系統,驗證了PⅠ(proportional-integral,比例-積分)控制算法的可靠性,但存在對高頻段控制效果不佳的問題;此外,還證明了LQG(linear quadratic Gaussian,線性二次高斯)控制和H∞算法能夠提高天線伺服控制系統的傳動性能,但因受到硬件的限制,控制效果不太理想。Lin等[7]將PⅠD控制與模糊理論相結合,用于改善天線的動態性能,該方法的控制效果較好。Tang 等[8]分析了PⅠ控制、LQG 控制、DFF(disturbance feed forward,擾動前饋)控制和DOBC(disturbance observer-based control,基于干擾觀測器的控制)下天線抗風擾的效果,結果表明,DOBC對風擾的抑制效果最好。
然而,上述針對天線伺服控制的研究通常將天線的反射面假設為剛性,即不考慮反射面的柔性變形,并將天線視為整體進行控制。但對于大口徑反射面天線,其反射面表面的結構變形對波束指向的影響不能忽略,因此須對反射面的變形機理進行研究。現階段,天線反射面風載特性的研究方法主要包括理論分析、數值模擬、風洞試驗以及現場實測等。因受制于成本、普適性和實驗難度等,數值模擬是目前最常用的技術手段。數值模擬是指利用CFD(computational fluid dynamics,計算流體動力學)方法,通過計算機對物體的風載特性進行仿真分析,其優勢是計算成本低、不受尺寸限制,且可以較方便地獲得不同工況下的風載特性[9]。Young等[10]針對風載荷對雙子座望遠鏡的球形保護罩的影響進行了數值模擬,結果表明,不同風場環境下球形保護罩的風載特性不同。Du等[11-12]對相控陣雷達的風載特性進行了數值模擬。王春圓、劉巖等[13-14]對大型射電望遠鏡的風載特性進行了數值模擬,并通過與風洞試驗結果進行對比來驗證數值模擬的準確性。Ladd 等[15]對GMT(giant Magellan telescope,巨型麥哲倫望遠鏡)進行了CFD數值模擬,所得結果可為望遠鏡的結構設計、選址提供參考。綜上,國內外學者雖已利用數值模擬及風洞試驗等方法對大口徑反射面天線的風載特性進行了分析,但對其面形精度和波束指向特性等的分析較少。
為此,筆者以奇臺射電望遠鏡(Qitai radio telescope, QTT)的110 m 大口徑反射面天線為研究對象,利用CFD數值模擬方法來分析和計算風擾情況下天線反射面表面的風壓系數和變形情況,并結合天線結構的變形情況對其波束指向特性的變化規律進行研究,旨在為大口徑反射面天線的抗風結構設計與系統控制研究提供理論指導。
1 大口徑反射面天線風場的數值模擬
CFD數值模擬具有控制方便、成本低、易模擬各種環境、可重復操作以及可獲得豐富的可視化信息等優點,常被用于大型結構的風場研究[16]。CFD數值模擬流程主要分為三部分:前處理、求解和后處理,具體如圖1所示。
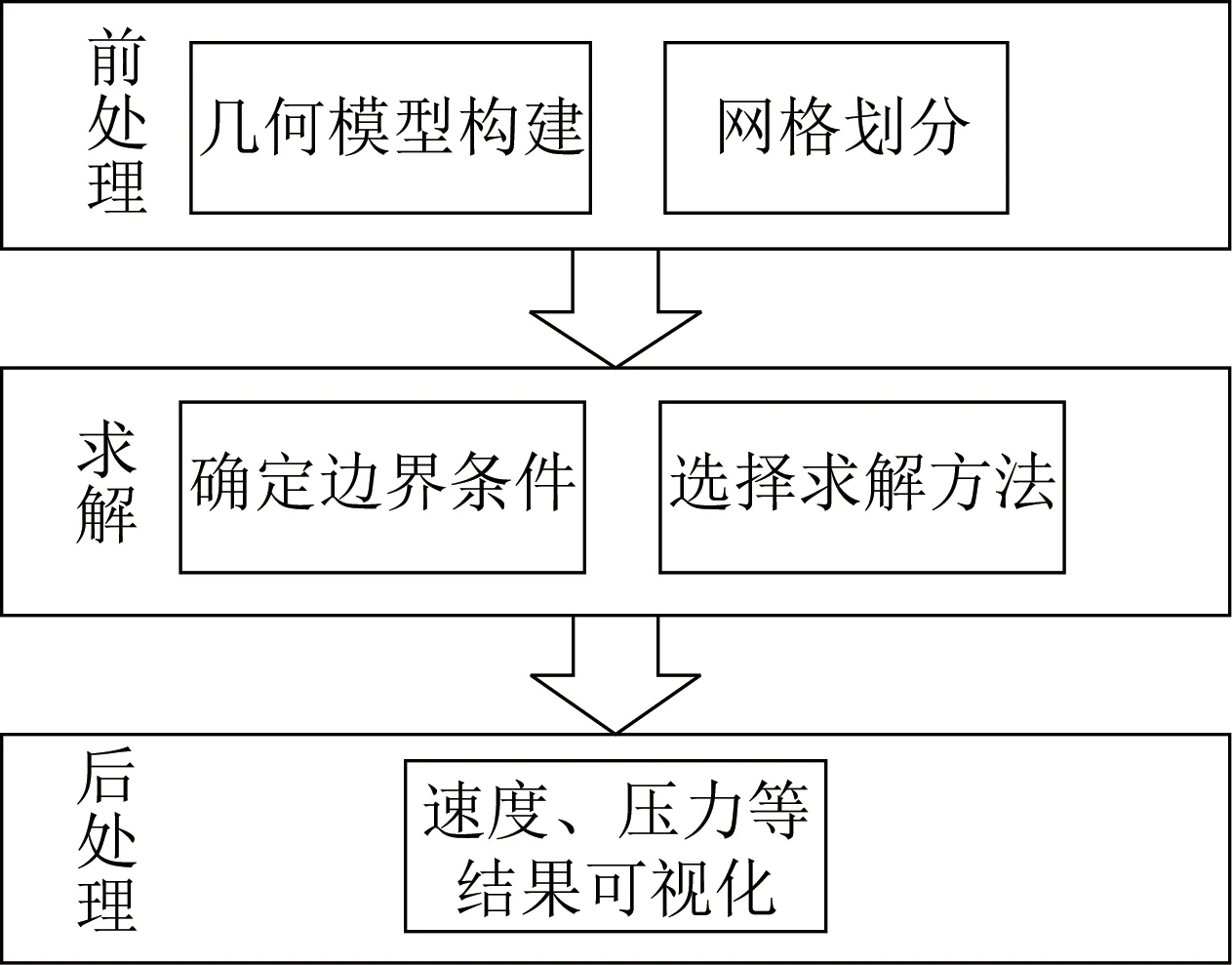
圖1 CFD數值模擬流程Fig.1 CFD numerical simulation process
根據圖1所示流程,首先采用Space Claim軟件對QTT 的110 m 大口徑反射面天線進行風場建模,然后采用Fluent軟件對天線反射面表面的風壓分布情況進行數值模擬,最后使用Tecplot軟件對天線反射面表面的風壓系數進行可視化后處理。
1.1 天線計算域模型的構建
由于受到網格生成方法的限制,在天線桁架桿件處無法有效劃分出合適的網格,且反射面的背架結構對反射面風壓分布的影響較小,故在劃分網格時,忽略背架結構,僅建立天線反射面的拋物面模型,以分析其風壓分布情況。計算域是指流體流經的區域,對于外部流動,計算域的邊界應遠離天線模型,以使湍流運動充分發展。若計算域尺寸過大,則會導致網格數量增加,從而造成計算量增大,這會大大降低計算效率,因此須對計算域模型的尺寸進行限制。
反射面天線計算域的尺寸參數包括高度H、上游尺寸L1、下游尺寸L2和寬度B等。為避免阻塞效應對天線結構周圍的流場產生干擾,同時保證計算速度,通常要求阻塞率不大于3%。當天線反射面的直徑為D時,根據文獻[13]確定天線計算域尺寸,具體如下:
根據阻塞率的計算公式和上述尺寸參數,可得:
式中:γ為阻塞率。
由式(1)可知,阻塞率滿足要求。基于上述尺寸參數,建立大口徑反射面天線的計算域模型,如圖2所示。
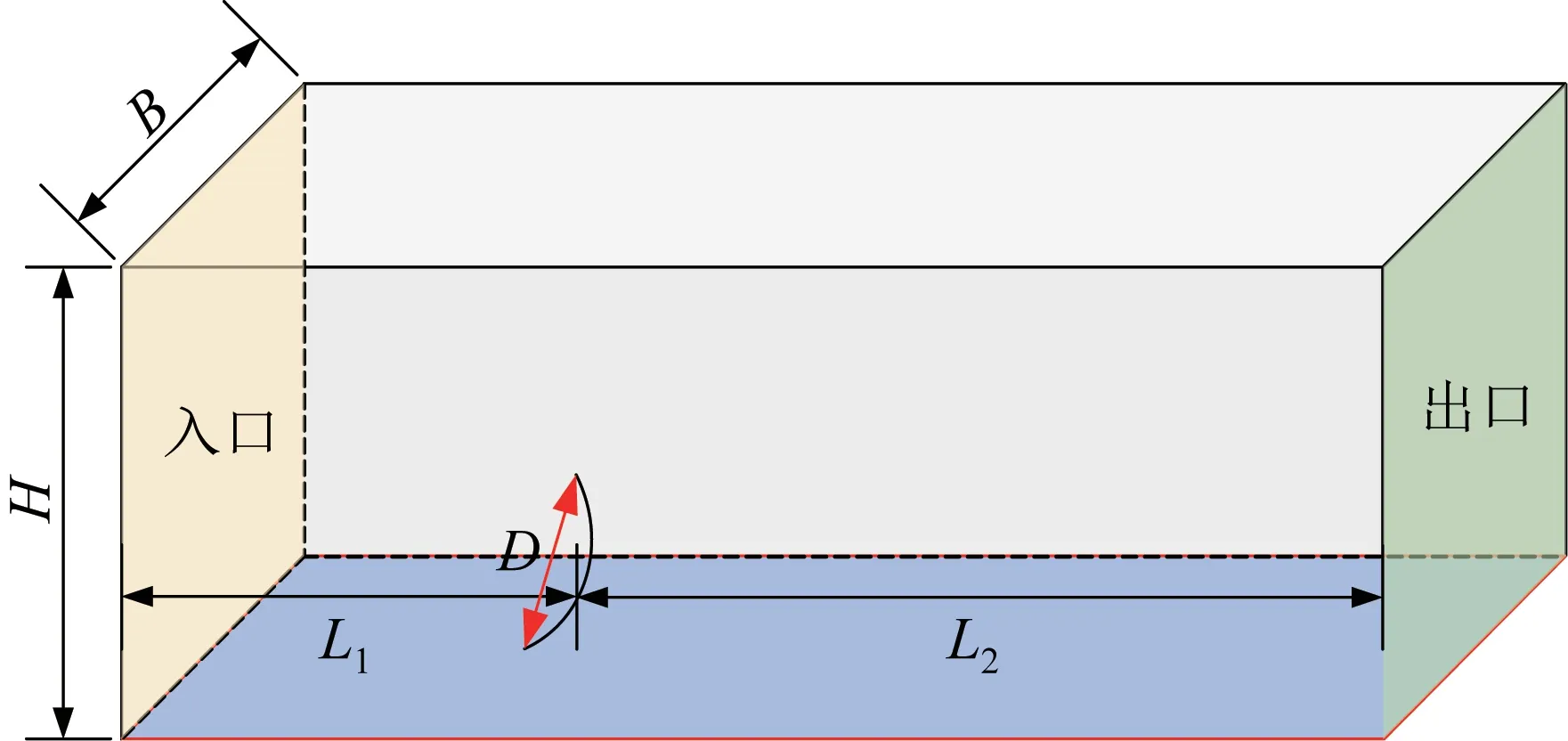
圖2 大口徑反射面天線計算域模型Fig.2 Computational domain model of large aperture reflector antenna
1.2 天線反射面表面風壓系數的計算
在求解前,應對大口徑反射面天線計算域模型設置合適的邊界條件:入口設為風的速度入口,假設出口處所有物理變量的法向梯度均為零;計算域的上表面及2個側面為滑動壁,計算域底面和天線反射面為非滑動壁。另外,在計算前還須對整個計算域進行網格劃分。鑒于非結構化網格具有較好的自適應性,能夠解決復雜流場的網格劃分問題,本文采用非結構化網格單元對所構建的計算域模型進行網格劃分。
RANS (Reynolds-averaged Navier-Stokes,雷諾平均湍流模型)通過引入合理的湍流模型來對雷諾應力項進行求解,該模型在求平均風壓等方面具有明顯優勢[17]。鑒于SSTk-ω模型對近壁面的模擬精度較高,本文采用該湍流模型對天線的流固耦合問題進行求解。在SSTk-ω模型中,動能k、湍流耗散率ε和比湍流耗散率ω的計算式如下:
式中:uz為任一高度處的平均風速;Ti為任意點處的溫度;Cμ為常數,常取0.09;l為湍流積分尺度。
利用Fluent軟件對大口徑反射面天線的網格模型進行求解,得到其反射面表面的風壓分布情況。通常情況下,采用風壓系數來描述風載荷對結構的力作用。結構表面風壓系數Cp的計算式如下:
式中:p為作用在結構表面的風壓,pref為參考點處的風壓,ρ為流體密度,v為參考點處的風速。
天線反射面表面所受的實際壓力為正、背面的壓力差,則風壓系數Cp可表示為:
式中:Cp_f、Cp_b分別為反射面正、背面的風壓系數。
根據式(3)和式(4),通過CFD 數值模擬得到天線反射面表面的風壓系數分布情況。由于天線反射面表面的風壓系數與風速無關,因此僅計算某一風速下反射面表面的風壓系數,即可獲得不同風速下天線反射面的風載特性。為探究俯仰角變化對天線反射面風載特性的影響,對天線方位角為0°、俯仰角不同(分別為5°,15°,30°,45°,60°,75°,90°)的工況下反射面正、背面的風壓系數進行計算,結果如表1所示。
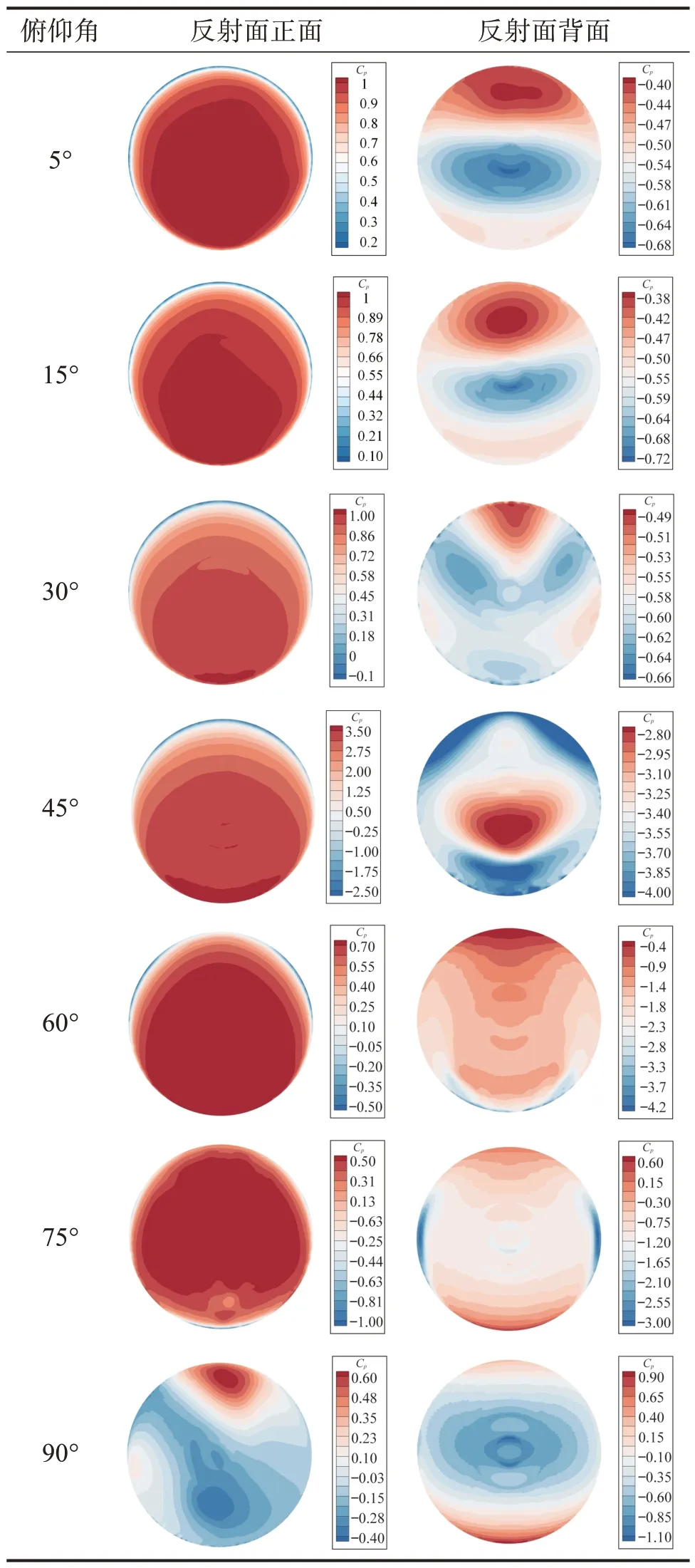
表1 不同俯仰角下天線反射面表面的風壓系數Table 1 Wind pressure coefficient on antenna reflector surface under different pitch angles
由表1所示的天線反射面正、背面的風壓系數分布情況可以看出,不同工況下最大變形均出現在反射面邊緣,且多為迎風口邊緣。這是因為來風在天線反射面的邊緣被分開,迎風處反射面正面的風向上產生正壓,背面的風向下產生渦流,形成負壓,正、背面的作用效果疊加,產生較大風壓。此外,在某些俯仰角工況下,風會在天線反射面的背面產生繞流,進而導致反射面邊緣處的風壓較大。
對天線反射面面板由內向外、按逆時針方向進行編號,由此得到不同反射面面板表面的風壓系數隨俯仰角的變化情況,如圖3(a)所示。以天線俯仰角為75°的工況為例,詳細展示天線第9 環、第16環反射面面板表面的風壓系數,如圖3(b)至圖3(d)所示。由圖3可以看出,天線反射面左右兩側邊緣處的風壓系數較大。

圖3 天線反射面面板表面風壓系數隨俯仰角的變化趨勢Fig.3 Variation trend of wind pressure coefficient on antenna reflector panel surface with pitch angles
2 大口徑反射面天線結構變形及面形精度分析
2.1 天線結構變形的有限元分析
對于所研究的110 m 大口徑反射面天線,本文只分析其反射面的流固耦合變形,即在有限元模型中將風載荷以風壓的形式直接作用于反射面上,從而分析反射面的結構變形。為方便計算,分析時對天線的有限元模型進行簡化,只建立反射面及背架結構的模型,將約束點設置在背架結構上,并在反射面上施加壓力載荷。
鑒于直接利用天線反射面上網格節點處風壓系數計算風載荷的過程非常復雜,為確定用于后文結構變形分析的風載荷值,擬對反射面進行區域劃分。反射面表面的風壓系數采用所有網格節點處的平均風壓系數來近似表示,隨后基于該平均風壓系數來計算反射面所受的壓力,并將壓力平均分布至反射面面板的各個頂點上。圖4所示為天線反射面表面的平均風壓系數的近似計算示意。
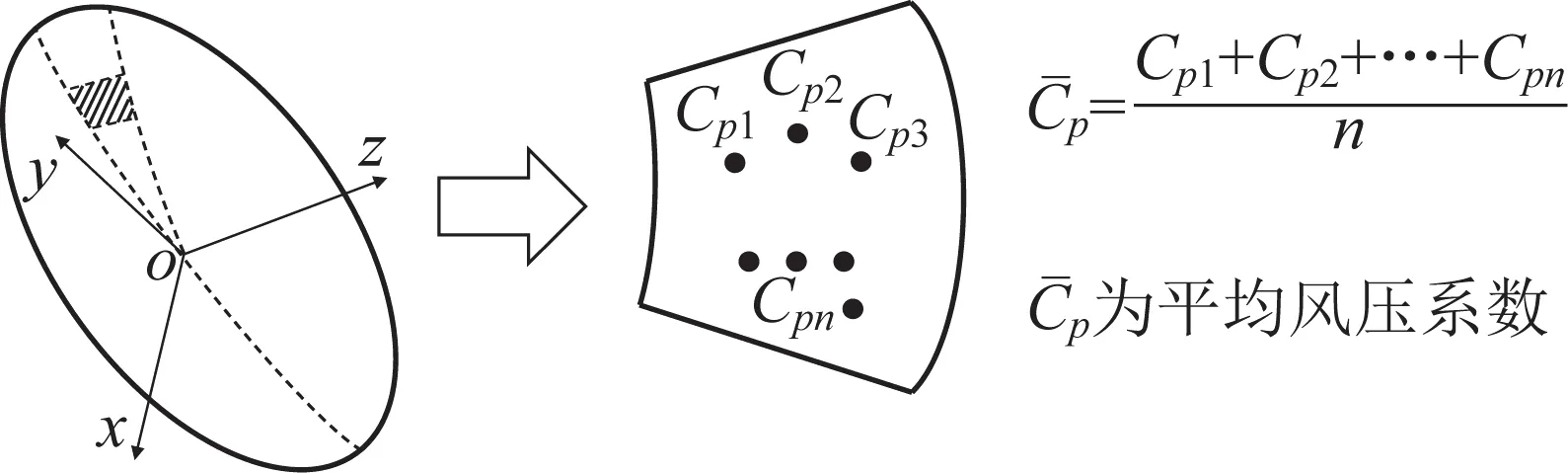
圖4 天線反射面表面平均風壓系數的近似計算Fig.4 Approximate calculation of average wind pressure coefficient for antenna reflector surface
根據平均風壓系數,可以計算出每一塊反射面面板上的均布載荷,其計算式如下:
式中:F為反射面面板所受的力,A為單一反射面面板的面積,Cˉp為反射面表面的平均風壓系數。
在天線有限元模型中,將每一塊反射面面板所受的載荷平均分布到4個頂點處,即可將流固耦合問題轉換為靜力學問題,通過靜力學有限元分析可快速計算得到天線反射面的結構變形。
根據文獻[18],大口徑反射面天線選址一般選擇風速較小處,QTT臺址處風速不大于6 m/s(四級風)的比例為87.7%。基于此,以四級風為例,計算不同俯仰角工況下天線反射面的變形情況,結果如圖5所示。
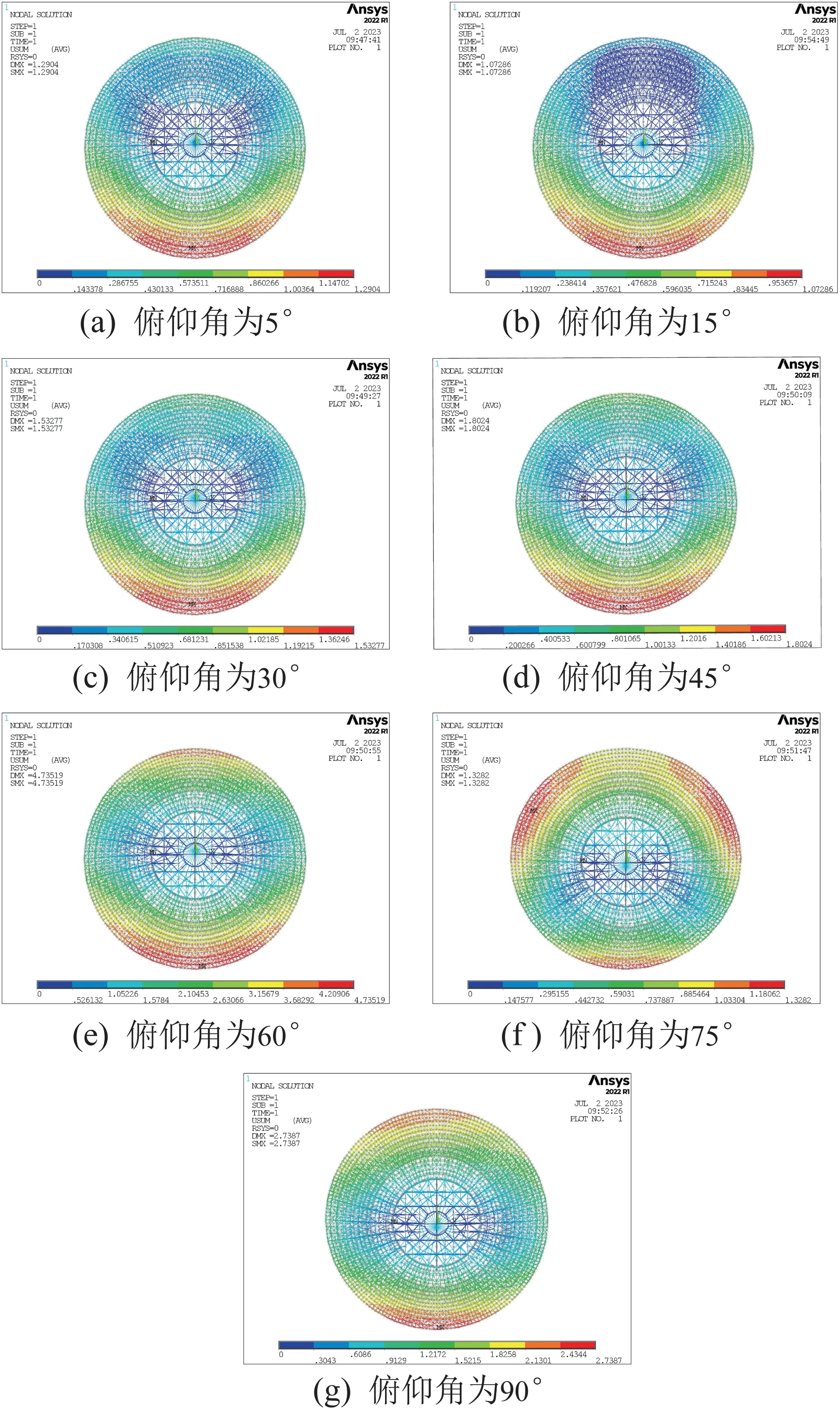
圖5 不同俯仰角下天線反射面的變形情況Fig.5 Deformation of antenna reflector under different pitch angles
由圖5可以看出,6 m/s風速下天線反射面變形的變化趨勢與風壓系數的變化趨勢相對應;當俯仰角較小時,天線下端迎風口區域的變形量最大。
圖6所示為6 m/s風速下天線反射面的變形極值隨俯仰角的變化趨勢。一般情況下,風壓系數較大時,天線反射面的變形也較大。但由圖6可知,俯仰角為90°時反射面表面的風壓系數不大,而結構變形卻較大。出現這一現象的原因如下:在其他俯仰角工況下,反射面表面的風壓系數均為正值,而當俯仰角為90°時,風直接吹到反射面的背面,使得反射面表面上一部分的風壓系數為負值,導致反射面受到了較強的傾覆力矩,從而產生了較大的變形。

圖6 不同俯仰角下天線反射面的變形極值Fig.6 Extreme value of deformation of antenna reflector under different pitch angles
2.2 天線面形精度分析
通常采用結構變形量的均方根誤差(root mean square error, RMSE)作為衡量天線反射面變形程度的指標。對不同風速、俯仰角工況下天線反射面變形量的RMSE進行計算,結果如圖7所示。

圖7 不同風速、俯仰角下天線反射面變形量的RMSEFig.7 RMSE of antenna reflector deformation under different wind speeds and pitch angles
由圖7可以看到,隨著風速的提高,天線反射面變形量的RMSE 逐漸增大;在天線俯仰角為60°的工況下,反射面的變形較嚴重,應作為控制調節的關注重點。
3 大口徑反射面天線波束指向分析
結構變形會影響天線的電性能,從而導致增益損失、指向偏差等問題。從天線的方向圖中可以看出天線在空間各個方向上接收電磁波的能力。通過繪制不同工況下大口徑反射面天線的方向圖,即可得到其波束指向的變化情況。
文獻[19-20]指出,物理光學法可以準確地分析大口徑反射面天線主、副瓣的特性。為此,本文基于物理光學法,將反射面的變形轉換為相位誤差并引入到天線電性能的積分公式中,則反射面天線遠區輻射電場的計算式可表示為:
其中:
式中:E為遠區輻射電場,(θ,?)為遠場觀測方向,h為自由空間波數,η為自由空間波阻抗,為等效面電流,r為遠場觀測點指向坐標原點的矢量,J為口徑面等效面電流,δ為口徑面的相位誤差,σA為反射面在口徑面上的投影面,Δz為軸向變形,θs為饋源坐標系os-xsyszs下反射面節點矢量與zs軸的夾角。
根據2.1 節,可以得到天線反射面上各點的徑向位移。由于CFD數值模擬耗時較長,為了快速計算得到不同俯仰角、風速工況下天線電性能的變化,可先提前計算并存儲反射面表面的風壓系數,隨后即可快速計算得到相應風速下反射面的結構變形量,最后根據變形量得到天線的方向圖,以分析其波束指向特性。大口徑反射面天線波束指向的分析流程如圖8所示。

圖8 大口徑反射面天線波束指向分析流程Fig.8 Analysis process for beam pointing of large aperture reflector antennas
利用文獻[21]中的方法,對式(6)的指數誤差項ejδ進行分段線性擬合,從而得到變形后天線的方向圖。圖9 所示為不同俯仰角工況下四級風(6 m/s)正吹時天線的方向圖。圖中:E面表示平行于電場方向的平面,H面表示平行于磁場方向的平面。由圖9可以看到,天線的電性能隨俯仰角的變化而變化,且變化程度與反射面的結構變形有關。從E面方向圖中可以看出,天線的增益損失較大,從H面方向圖中可以看到,天線的波束指向偏差較大。

圖9 6 m/s風速下天線的方向圖Fig.9 Directional pattern of antenna at 6m/s wind speed
圖10 所示為6 m/s 風速下天線的增益損失隨俯仰角的變化趨勢。從圖10中可以看出,天線的增益損失與反射面的結構變形呈正相關;在不同俯仰角工況下,反射面的結構變形越大,天線的增益損失越嚴重,則其觀測性能越差。
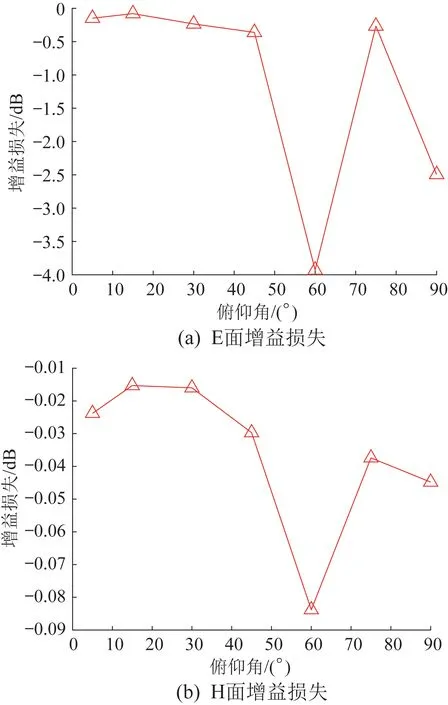
圖10 6 m/s風速下天線的增益損失Fig.10 Gain loss of antenna at 6 m/s wind speed
當天線在工作時,若其副瓣電平抬高,則會導致主瓣的能量降低,這不利于天線接收信號。天線副瓣電平越低,表示其抗干擾的能力越強。圖11所示為6 m/s風速下天線第一副瓣電平隨俯仰角的變化情況。從圖11中可以看到,在增益損失較大的不利工況下,天線第一副瓣電平會抬高,導致天線的觀測性能下降。
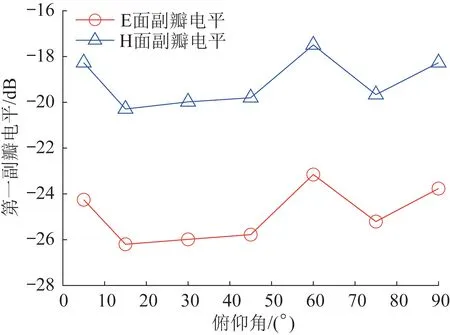
圖11 6 m/s風速下天線第一副瓣電平的變化情況Fig.11 Variation of the first sublobe level of antenna at 6 m/s wind speed
4 結 論
本文采用CFD 數值模擬方法分析了大口徑反射面天線表面風壓系數的分布情況,從而得到了其風載特性。隨后,利用風壓系數計算了天線各反射面面板所受的風載荷,并對天線進行有限元仿真分析,得到了天線的結構變形規律。最后,通過天線結構變形量—電磁場的耦合計算,得到了其反射面波束指向特性的變化情況。具體結論和建議如下:
1)天線反射面迎風口處所受的風壓較大,且此處的變形較大,在后續的柔性控制中應重點關注。
2)某些工況下天線的結構變形和波束指向偏差較大,故不同工況的控制應具有針對性。
3)由于天線的結構復雜,本文僅考慮了反射面的變形情況,后續研究應綜合考慮其他結構的變形。
通過分析大口徑反射面天線的風載特性可以快速計算得到其反射面的結構變形以及電性能的變化情況,這可為天線的風擾控制提供參考。

