接縫弱化后縱連板式無砟軌道溫度效應研究

曹毅杰，蔣典佑，劉 鈺，孫曉丹，朱星盛，谷永磊

(1.西南交通大學土木工程學院,成都 610031; 2.京滬高速鐵路股份有限公司,北京 100038)

引言

縱連板式無砟軌道作為我國主要軌道結構形式之一,已在京津、京滬、京廣等高速鐵路上廣泛應用。在運營過程中受極端氣候條件的影響,軌道結構發生了不同程度的損傷,主要表現為:軌道板與CA砂漿層間離縫、板間接縫擠碎或拉裂、支撐層擠壓斜裂和軌道板上拱等現象[1-5],其中,以夏季持續高溫天氣下縱連式軌道板在寬窄接縫處出現的上拱病害最為突出,軌道板上拱引起的鋼軌豎向位移局部增大將破壞線路的高平順性,嚴重時甚至威脅高速列車的運營安全。目前,基于軌道板上拱病害特征,存在上拱風險的區段往往通過植筋的方式對既有軌道結構進行加固和補強[6];而對于已經發生上拱病害的區段,通過先鑿除后填補的方式進行修復[7]。然而,這些措施難以從根本上解決軌道板上拱問題,高溫天氣下,軌道板內部依舊積存巨大的溫度應力。因此,釋放軌道板內的溫度應力,從根本上減少病害的產生,對緩解持續高溫天氣下的軌道板上拱具有重要的現實意義。

目前,針對極端條件下縱連板式無砟軌道上拱整治研究已取得一定進展。部分學者在不改變現有長縱連體系基礎上,對具體施工措施展開研究。如文獻[8-13]通過分析植筋錨固對上拱預防和整治的影響,給出合理的植筋建議,為現場維修提供參考;文獻[14]介紹在無砟軌道板上涂刷反射隔熱層的方法預防軌道板上拱。以上學者均對軌道板上拱整治做出了一定貢獻,但未從應力釋放的角度考慮病害整治。對此,另有部分學者嘗試把長縱連體系轉化為弱縱連體系或單元體系,并已取得一定成果。如文獻[15-16]提出采用換填寬窄接縫的整治方案,分析不同彈性模量的寬窄接縫對軌道結構受力和變形特征的影響。然而學者們研究時尚未考慮材料的非線性變形,也未充分考慮軌道結構的層間黏結關系。文獻[17]通過將縱連式軌道結構解鎖成單元結構的方式,引入內聚力單元和混凝土損傷塑性本構,分析解鎖成單元結構后的溫度適應性。但縱連結構轉化成單元結構后,需要通過植筋來約束縱向位移,在一定程度上增加了施工作業量,大大提高了維修成本。為此,采用折中的方式,在寬窄接縫處設置一定厚度、彈性模量較小的填充層,將原有縱連體系轉化成弱縱連體系,保證應力釋放的同時,不會產生較大的縱向變形,有利于解決夏季脹板問題。

因此,通過建立設有彈性填充層的縱連板式無砟軌道數值模型,引入內聚力單元和混凝土損傷塑性本構,分析設置彈性填充層后,在整體溫升作用下軌道結構應力、變形和損傷的變化情況,并探討節段長度和彈性模量對應力、變形以及損傷的影響。

1 模型介紹

1.1 數值模型

利用ABAQUS建立設置彈性填充層后的縱連板式無砟軌道數值模型,見圖1。由圖1可知,模型由鋼軌、扣件、軌道板、寬窄接縫、彈性填充層、CA砂漿、底座板和基礎組成。軌道板寬2 550 mm,底座板寬2 950 mm,基礎寬3 950 mm;軌道板厚200 mm,CA砂漿層厚30 mm,底座板厚200 mm。寬接縫縱向長210 mm。窄接縫縱向長50 mm,寬窄接縫厚度均為100 mm,在寬窄接縫縱向兩側分別設置縱向長10 mm的彈性填充層。模型長度考慮3塊板一節段和4塊板一節段,模型采用1.5塊+1.5塊軌道板和2塊+2塊軌道板的布置形式,如圖2所示。模型兩端設置對稱約束,梁底面節點全約束。模型所有部件施加整體溫升。

圖1 縱連板式無砟軌道數值模型(單位:mm)

圖2 不同節段長度模型整體示意

模型中鋼軌采用CHN60軌,利用實體單元模擬;扣件利用三向非線性彈簧模擬,扣件間距650 mm,扣件垂向、橫向剛度均為25 kN/mm,每組扣件縱向阻力15 kN,彈塑性臨界點2 mm;軌道板、寬窄接縫、CA砂漿和底座板均采用實體單元模擬,基礎采用剛體模擬。鋼軌、軌道板、寬窄接縫、CA砂漿和底座板的材料參數見表1。模型在軌道板與CA砂漿層之間采用1 mm的內聚力單元模擬界面黏結作用,離縫產生時,層間接觸屬性設為面面接觸。假設彈性填充層與軌道板和寬窄接縫黏結完好,又因為縱向連接鋼筋對接縫存在約束作用。因此,彈性填充層分別與軌道板和寬,窄接縫設置共節點約束,設有彈性填充層的新接縫底面與CA砂漿設置面面接觸,其中法向為硬接觸,切向摩擦系數設置為0.5。CA砂漿和底座板之間采用綁定約束;底座板底面與基礎設置面面接觸,其中法向為硬接觸,切向摩擦系數設置為0.3。

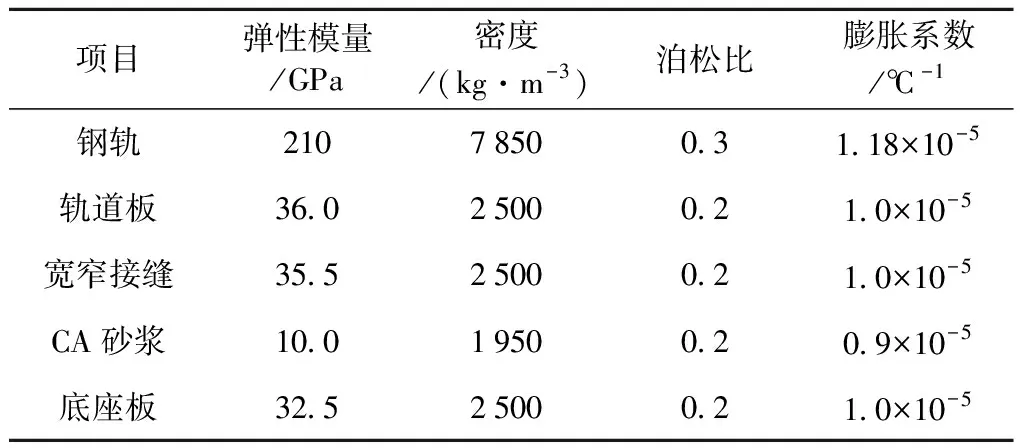
表1 CRTSⅡ型板式無砟軌道主要結構參數

1.2 層間界面內聚力模型

為描述軌道板與CA砂漿層的層間界面力-位移關系,采用圖3所示的雙線性內聚力模型。

圖3 雙線性型內聚力模型

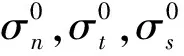
(1)

當層間界面出現損傷后,界面強度可由下式計算得到

(2)

式中,δn,δs分別表示對應的法向位移和切向位移;Dcoh表示內聚力單元的損傷,介于0～1之間,由下式計算

(3)

(4)

假定層間界面切向性能均勻連續,則有GⅡC=GⅢC。本文數值模擬采用的雙線性內聚力模型,其法向和切向內聚力參數參照《京滬公司推板試驗研究報告》[18],列于表2。

表2 雙線性型內聚力模型參數

1.3 混凝土損傷判別因子

采用混凝土損傷塑性模型模擬混凝土的失效行為,并引入混凝土損傷因子Di[19-20]描述混凝土的損傷情況,Di介于0～1之間,0表示混凝土未損傷;1表示混凝土完全損傷。

(5)

式中,i為混凝土受力狀態;i=t時表示混凝土受拉;i=c時表示混凝土受壓;σi和εi為混凝土單軸受拉(壓)應力和應變;Ei為混凝土的彈性模量。根據GB 50010—2010《混凝土結構設計規范》[21],σi和εi關系為

σi=(1-di)Eiεi

(6)

式中,di為混凝土單軸受拉(壓)損傷演化參數。

(7)

(8)

式中,αi為混凝土單軸受拉(壓)本構關系曲線下降段參數;x,n和ρi分別為

(9)

式中,fi,r為混凝土單軸抗拉(壓)強度代表值;εi,r為對應抗拉(壓)強度的峰值應變。

混凝土塑性損傷模型相關參數見表3。

表3 混凝土塑性損傷材料力學參數

1.4 模型驗證

參照鐵科院《CRTSⅡ型板式無砟軌道溫度變形與控制措施研究總報告》[22]中軌道板上拱試驗,如圖4所示。考慮既有線軌道板上拱大部分都發生在接縫處,將寬窄接縫重新灌注,窄接縫不灌注,模擬現場施工過程中窄接縫灌注質量缺陷,來判斷誘發軌道板上拱變形的成因。現場試驗通過對軌道縱向兩端施加推力來等效結構的整體溫升,對此先建立CRTSⅡ型板式無砟軌道計算模型,并將模型中的窄接縫移除,見圖5。對模型兩端施加縱向推力所等效的溫升,最終選取軌道板上、下表面應力與上拱量對應關系作對比驗證,見圖6。由圖6可知,模擬結果與實測曲線基本吻合,表明本文建立的CRTSⅡ型板式無砟軌道溫度應力計算模型合理可靠。

圖4 軌道板上拱試驗

圖5 有限元計算模型

圖6 有限元計算與試驗對比驗證

2 整體溫升下軌道板應力、變形和損傷分析

為更直觀地表現出設置彈性填充層后軌道板頂、底面的應力釋放情況,以彈性填充層彈性模量1 775 MPa,節段長度3塊板的結果為例,根據圖7路徑所示,沿路徑方向提取整體溫升10 ℃、20 ℃、30 ℃、40 ℃和50 ℃時,軌道板頂面和底面設置彈性填充層前后的縱向應力差(設置彈性填充層后的縱向壓應力-未設置彈性填充層的縱向壓應力),同時提取設置彈性填充層后的軌道板上下表面縱向應力差(設置彈性填充層后軌道板頂面的縱向壓應力-設置彈性填充層后軌道板底面的縱向壓應力),見圖8,其中,0 m處為設置彈性填充層的接縫縱向中心。

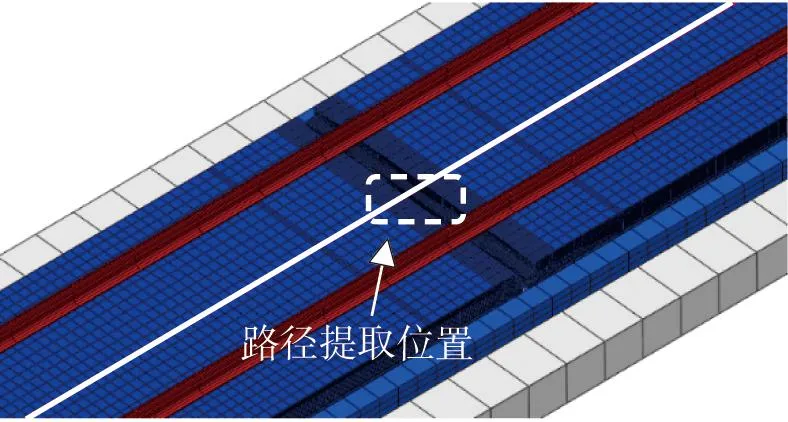
圖7 路徑提取示意

圖8 路徑上應力差分布

由圖8可知,軌道板頂、底面設置彈性填充層前后的縱向應力差存在負值,說明設置彈性填充層后,軌道板頂、底面應力得到釋放;反之,出現正值,說明軌道板頂、底面應力出現了應力增加。對于設置彈性填充層后的軌道板上下表面應力差,當值不為0時,說明出現偏心作用。接縫弱化后,整體溫升10 ℃時,0.25 m以外應力差基本為零;0.25 m以內出現應力波動,寬接縫頂面和軌道板底面出現應力釋放,最大達到2.27 MPa,窄接縫底面和軌道板頂面出現少量應力增加。由此說明,溫升較低時,彈性填充層對軌道板的應力釋放有限。整體溫升增大至30 ℃,0.25 m以外軌道板頂、底面出現少量應力釋放,達到0.4 MPa;0.25 m以內應力釋放量和應力增加量均隨溫升增大而增大。由于彈性填充層彈性模量較小,整體溫升作用下變形比軌道板和接縫大,同時又受寬窄接縫T形構造的影響,局部區域的軌道板和接縫均出現偏心作用,見圖8中藍線。對比偏心作用位置和縱向應力差出現波動位置可得,偏心作用是導致軌道板出現應力增加的主要原因。

整體溫升40 ℃時,偏心作用開始向遠離彈性填充層的方向擴展,應力波動范圍增大,0.35 m以外,軌道板頂面和底面應力釋放量達到0.6 MPa;0.35 m以內,應力釋放量和應力增加量繼續增大,最大應力釋放量達到6.39 MPa。

然而,隨著溫升繼續增大,應力釋放量開始減小,整體溫升50 ℃時,應力釋放量為5.75 MPa,下降10%。其原因是整體溫升50 ℃時,接縫和軌道板均發生了一定程度的損傷,見圖9。在損傷和偏心的相互作用下,應力釋放受到抑制。觀察圖9發現,整體溫升50 ℃時,損傷主要集中在接觸位置,這是因為彈性填充層彈性模量較低,相同溫度力作用下縱向變形較大,又受到偏心作用的影響,使得彈性填充層與接縫和軌道板的接觸不均勻,從而導致損傷發生并集中在接觸面上。

圖9 損傷示意

圖10為沿圖7路徑提取整體溫升50 ℃時,軌道板和底座板的縱向位移分布。由圖10可知,底座板縱向位移最大值0.024 mm,軌道板縱向位移最大值0.096 mm,后者縱向位移是前者的3倍。由此說明,設置彈性填充層會使得軌道結構層間變形難以協調,進而導致層間損傷發生的臨界溫升降低,層間損傷演化過程見圖11。由圖11可知,當整體溫升達到23 ℃時,層間發生損傷,損傷出現在縱向靠近彈性填充層一端,隨著溫升不斷增加,損傷逐漸向遠離彈性填充層方向擴展。當溫升達到50 ℃時,損傷最大值發生在縱向靠近彈性填充層端部,達到0.66。

圖10 路徑上的縱向位移分布

圖11 層間損傷演化過程

由于設置彈性填充層后層間損傷在較低溫升下就會發生,因此損傷區的黏結強度有所下降,再加上偏心作用的影響,彈性填充層旁軌道板和接縫難免會產生一定上拱量,最終映射到鋼軌上,從而影響行車安全。因此,提取鋼軌、接縫、軌道板和底座板設置彈性填充層后的最大上拱增量(設置彈性填充層后豎向位移最值-未設置彈性填充層豎向位移最值)隨整體溫升的變化過程,見圖12。

圖12 不同結構層最大上拱增量隨溫升變化情況

由圖12可知,設置彈性填充層后,鋼軌上拱量未增加。對于接縫,其上拱增量的增長速率隨著溫升增大不斷提高;對于軌道板,溫升較低時,其上拱增量為負,隨著溫升增大,上拱增量逐漸由負轉正,并且增長速率也越來越大。由圖8可知,接縫位置處存在較大偏心力,在偏心作用下,接縫上凸會導致相鄰兩側軌道板板端下凹,從而使得上拱增量為負值。當溫升不斷增大后,混凝土自身受熱膨脹以及偏心作用范圍的增加,導致軌道板上拱增量由負轉正,最終增長速率越來越大。對于底座板,彈性填充層對其影響很小,上拱增量僅0.003 mm。盡管接縫和軌道板在設置彈性填充層后增加了一定的上拱位移,但鋼軌上拱位移未增加,未設置彈性填充層的鋼軌豎向位移為0.38 mm,在規范[23]允許范圍內(±2 mm)。

3 損傷、應力和鋼軌上拱量影響分析

為探討3塊板和4塊板兩種節段長度以及彈性填充層彈性模量對損傷、應力、軌道板和鋼軌豎向位移的影響,設計彈性填充層彈性模量分別為17 750,3 550,1 775,355,177.5 MPa,同時計算未設置彈性填充層的原始工況(35 500 MPa)進行對比。

3.1 對損傷的影響

圖13為不同彈性模量下,整體溫升50 ℃時,節段長度3塊板和4塊板的接縫、軌道板和層間損傷最大值。

圖13 不同工況下損傷情況

由圖13可知,不同節段長度下,軌道板、接縫和層間界面損傷均隨彈性模量降低逐漸增大。相同彈性模量下,節段長度4塊板的接縫和軌道板損傷大于節段長度3塊板的接縫和軌道板損傷。當節段長度為4塊板,彈性模量等于1 775 MPa時,接縫損傷已大于0.8,此時損傷區已很難再承受溫度應力。當節段長度為3塊板,彈性模量等于355 MPa時,接縫和軌道板損傷均已大于0.8,此時結構同樣很難再承受溫度應力。對于層間界面,3塊板與4塊板的損傷基本相同,當彈性模量低于355 MPa時,損傷大于0.9,軌道板與CA砂漿層之間即將出現離縫。

3.2 對應力的影響

提取兩種節段長度在整體溫升50 ℃時,不同彈性模量下,設置彈性填充層前后接縫和軌道板縱向應力釋放量最大值,見圖14。

由圖14可知,兩種節段長度下,隨著彈性模量降低,接縫和軌道板的應力釋放量均逐漸增大,并且接縫的應力釋放量大于軌道板的應力釋放量。對于軌道板,節段長度3塊板的應力釋放量始終大于節段長度4塊板的應力釋放量,最大應力釋放相差達到5.42 MPa。這是因為節段長度4塊板的軌道板損傷大于節段長度3塊板的軌道板損傷,軌道板塑性損傷越大,其抗壓能力就越弱,自身能夠承受的壓力越小,最終限制了應力釋放。對于接縫,彈性模量不小于355 MPa時,節段長度3塊板的應力釋放量大于節段長度4塊板的應力釋放量;彈性模量小于355 MPa時,節段長度3塊板的應力釋放量逐漸小于節段長度4塊板的應力釋放量。

由前文分析可知,設置彈性填充層后,軌道板局部區域會受到偏心作用,導致其出現應力增加。因此,提取兩種節段長度在整體溫升50 ℃時,不同彈性模量下,設置彈性填充層前后軌道板縱向應力增加量最大值和軌道板上下表面應力差最大值,見圖15。

圖15 不同工況下軌道板應力增量和上下表面應力差

由圖15(a)可知,隨著彈性模量降低,兩種節段長度下的軌道板應力增加量均逐漸增大。彈性模量不低于1 775 MPa時,節段長度3塊板的應力增加量低于節段長度4塊板的應力增加量;彈性模量低于1 775 MPa時,節段長度3塊板的應力增加量逐漸高于節段長度4塊板的應力增加量。由圖15(b)可知,彈性模量不低于3 550 MPa時,兩種節段長度的偏心作用基本相同,隨著彈性模量降低,軌道板偏心作用逐漸增大。彈性模量177.5 MPa時,兩種節段長度的軌道板偏心作用最大相差7.19 MPa。其原因在于,彈性模量較大時,盡管兩種節段長度的溫度力不同,但溫度力導致彈性填充層的變形較小,因此,偏心作用差異不明顯;彈性模量較小時,溫度力導致彈性填充層變形較大,進而偏心作用的差異逐漸明顯。

3.3 對鋼軌上拱量的影響

圖16為設置彈性填充層后,不同彈性模量下,整體溫升50 ℃時,節段長度3塊板和4塊板的軌道板和鋼軌最大上拱增量(設置彈性填充層后的豎向位移-未設置彈性填充層的豎向位移)。

圖16 不同工況下的鋼軌和軌道板最大上拱增量

由圖16可知,兩種節段長度下,隨著彈性模量降低,軌道板和鋼軌最大上拱增量逐漸增大,彈性模量低于3 550 MPa后,節段長度4塊板的最大上拱位移增量大于節段長度3塊板的最大上拱位移增量。對于層間界面,節段長度4塊板的損傷略大于節段長度3塊板的損傷,層間損傷越大,界面黏結強度越低。同時,對于接縫和軌道板,節段長度4塊板的塑性損傷大于節段長度3塊板的塑性損傷,塑性損傷越大,結構自身的抗壓能力就會越弱。因此,在損傷的綜合作用下,節段長度4塊板的上拱增量大于節段長度3塊板的上拱增量。由于兩個節段長度下,未設置彈性填充層時鋼軌豎向位移均為0.39 mm,因此不同節段長度和不同彈模下的鋼軌豎向位移均在規范允許范圍內(±2 mm)。

4 結論

通過建立設有彈性填充層的縱連板式無砟軌道計算模型,引入內聚力單元和混凝土損傷塑性本構,分析整體溫升作用下,接縫弱化對軌道結構應力、變形和損傷的影響,并且探討了節段長度和彈性模量對應力、變形和損傷的影響,主要結論如下。

(1)設置彈性填充層后,軌道板和接縫的縱向應力均得到一定程度釋放,但接縫和軌道板局部區域會發生偏心作用,進而出現應力增加。此外,彈性填充層的設置也會使軌道結構層間變形難以協調,導致接縫、軌道板和層間界面損傷產生的臨界溫升較低。結構損傷較大時,軌道板和接縫的應力釋放會受到限制,并且彈性填充層附近也會產生一定上拱增量,最終在一定程度上影響行車安全。

(2)兩種節段長度下,軌道板、接縫和層間界面損傷會隨著彈性模量降低逐漸增大。相同彈性模量下,節段長度4塊板的接縫和軌道板損傷大于節段長度3塊板的接縫和軌道板損傷。

(3)隨著彈性模量降低,接縫和軌道板的應力釋放量均逐漸增大,最大應力釋放量發生在接縫處。此外結合損傷可得:節段長度為4塊板時,彈性填充層彈性模量選取建議高于1 775 MPa并低于3 550 MPa;節段長度為3塊板時,彈性填充層彈性模量選取建議高于355 MPa并低于1 775 MPa。

(4)兩種節段長度下,隨著彈性模量降低,軌道板和鋼軌最大上拱增量逐漸增大,彈性模量低于3 550 MPa后,節段長度4塊板的最大上拱位移增量大于節段長度3塊板的最大上拱位移增量。對于鋼軌,兩種節段長度下的豎向位移均在規范允許范圍內。