不完全信息Epsilon納什均衡的航天器末端追逃博弈策略

湯 旭，葉 東，肖 巖，孫兆偉

（哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所，哈爾濱 150001）

0 引言

隨著太空技術(shù)的不斷升級(jí)，空間航天器的功能日趨完備，越來(lái)越多的航天器具備了空間態(tài)勢(shì)感知的能力［1-2］。當(dāng)攔截航天器接近目標(biāo)航天器時(shí)，目標(biāo)方將采取機(jī)動(dòng)策略加以躲避，這使得攔截航天器控制系統(tǒng)在應(yīng)對(duì)新體系下迅速發(fā)展的空間攻防任務(wù)時(shí)面臨著困境［3］。因此，在爭(zhēng)奪戰(zhàn)時(shí)空間信息優(yōu)勢(shì)的過(guò)程中，亟待發(fā)展新的軌道控制策略。

針對(duì)此類具有自主機(jī)動(dòng)、自主決策能力的航天器攔截問(wèn)題，需要對(duì)連續(xù)動(dòng)態(tài)對(duì)抗的雙邊復(fù)雜態(tài)勢(shì)進(jìn)行研究，傳統(tǒng)的單邊優(yōu)化攔截控制方法將不再適用［4］。此時(shí)，攔截器與目標(biāo)存在利益沖突，構(gòu)成博弈關(guān)系，空間攔截、交會(huì)對(duì)接問(wèn)題也將發(fā)展成雙方航天器間的追逃博弈問(wèn)題［5］。此外，由于空間戰(zhàn)場(chǎng)環(huán)境的限制、航天器固定指向以及傳感器的約束，攔截器將不能完全獲悉目標(biāo)信息，導(dǎo)致攔截呈現(xiàn)不完全信息態(tài)勢(shì)。因此，研究不完全信息下的航天器軌道追逃問(wèn)題對(duì)于應(yīng)對(duì)未來(lái)空間領(lǐng)域的新形勢(shì)具有重要意義［6］。

針對(duì)目標(biāo)具有機(jī)動(dòng)能力的雙邊攔截博弈問(wèn)題，應(yīng)用最廣泛的研究方法是微分對(duì)策理論，該理論已成熟應(yīng)用于導(dǎo)彈攔截問(wèn)題中。文獻(xiàn)［7］基于簡(jiǎn)化的雙積分系統(tǒng)導(dǎo)彈攔截模型，設(shè)計(jì)了導(dǎo)彈攔截矢量制導(dǎo)率，并分別給出了制導(dǎo)率在極坐標(biāo)和球坐標(biāo)下的分量表示，以便在不同坐標(biāo)系下進(jìn)行描述。文獻(xiàn)［8］在攔截過(guò)程中考慮了存在角度測(cè)量有界噪聲的情況，通過(guò)設(shè)計(jì)狀態(tài)觀測(cè)器實(shí)現(xiàn)對(duì)角度的估計(jì)并分別給出了不同噪聲條件下脫靶量的估計(jì)值。文獻(xiàn)［9］針對(duì)制導(dǎo)率包含攔截剩余時(shí)間且該時(shí)間難以確定的問(wèn)題，建立了關(guān)于剩余時(shí)間的方程，并討論了該方程的分叉現(xiàn)象，以求解最短攔截時(shí)間，從而實(shí)現(xiàn)快速攔截。盡管微分對(duì)策理論在導(dǎo)彈領(lǐng)域得到了廣泛的應(yīng)用，但在太空領(lǐng)域中仍有較大的提升空間。

與傳統(tǒng)的空間交會(huì)攔截問(wèn)題相比，航天器追逃博弈策略需要考慮博弈雙方的控制策略。文獻(xiàn)［10］將非線性攔截逃逸相對(duì)動(dòng)力學(xué)簡(jiǎn)化為CW方程，根據(jù)攔截任務(wù)終止要求引入零控脫靶矢量將動(dòng)力學(xué)方程降階，采用攔截脫靶量和燃料消耗作為二次最優(yōu)目標(biāo)函數(shù)，推導(dǎo)了衛(wèi)星軌道次優(yōu)控制策略。文獻(xiàn)［11］則以CW 方程為基礎(chǔ)，推導(dǎo)了最優(yōu)推力角博弈策略，并采用粒子群優(yōu)化算法解決了協(xié)態(tài)變量初值難以確定的問(wèn)題，得到了開(kāi)環(huán)解。同時(shí)，通過(guò)預(yù)先生成一系列最優(yōu)軌跡，并進(jìn)行插值和外推，得到反饋控制策略的閉環(huán)解。文獻(xiàn)［12］考慮了航天器追逃的雙邊博弈問(wèn)題，提出了混合控制策略，以適配多任務(wù)的需求。通過(guò)博弈值函數(shù)與軌跡界柵判斷是否需要執(zhí)行策略切換，以實(shí)現(xiàn)追逃任務(wù)與自身任務(wù)的平衡。文獻(xiàn)［13-14］對(duì)航天器遠(yuǎn)程攔截博弈問(wèn)題進(jìn)行了研究，針對(duì)協(xié)態(tài)變量初值難以確定的問(wèn)題，通過(guò)遺傳算法優(yōu)化求解近似初值，然后將運(yùn)動(dòng)軌跡離散化，為各離散點(diǎn)配置狀態(tài)，并使用非線性規(guī)劃優(yōu)化求解協(xié)態(tài)變量初值的精確值。文獻(xiàn)［15］研究了航天器多段博弈攔截問(wèn)題：在遠(yuǎn)程攔截段，基于微分對(duì)策理論分別給出了閉環(huán)鞍點(diǎn)解和開(kāi)環(huán)鞍點(diǎn)解，兩組解在形式上相同；在近程攔截段，考慮不同的指標(biāo)函數(shù)，分別建立了不同的博弈策略。通過(guò)分析得出，實(shí)現(xiàn)攔截的充要條件是攔截器的推力幅值大于目標(biāo)的推力幅值。文獻(xiàn)［16］針對(duì)多航天器的末端攔截博弈問(wèn)題，根據(jù)攔截空間是否具有防御器將博弈態(tài)勢(shì)分為雙星博弈和三星博弈，并提出了一種博弈切換策略，將三星博弈轉(zhuǎn)化為分段的雙星博弈，并將雙邊時(shí)間方程擴(kuò)展到三星博弈中，使得攔截器能夠在不被防御器反攔截的情況下快速攔截目標(biāo)。

由于空間攻防時(shí)戰(zhàn)場(chǎng)的不確定性、信息不對(duì)稱等因素，航天器追逃任務(wù)中往往存在信息不完全的情況。因此，攔截航天器需要在有限時(shí)間內(nèi)對(duì)目標(biāo)航天器的不完全信息進(jìn)行估計(jì)，以便實(shí)施有效的機(jī)動(dòng)策略。在這種情況下，航天器追逃博弈理論可以為攔截任務(wù)提供有效的決策支持。針對(duì)不完全信息下的攔截問(wèn)題，文獻(xiàn)［17］研究了目標(biāo)的逃逸防御問(wèn)題，通過(guò)給定攔截器策略，考慮目標(biāo)與防御器之間存在單向通訊或雙向通訊的不同情況，建立了目標(biāo)與防御器間的最優(yōu)博弈策略。文獻(xiàn)［18-19］中使用雙積分系統(tǒng)作為動(dòng)力學(xué)模型來(lái)探究目標(biāo)信息不完全和動(dòng)力學(xué)信息不完美的情況，將不完全信息和不完美信息視為擴(kuò)展的狀態(tài)變量，采用了增廣原動(dòng)力學(xué)的方法處理信息缺失問(wèn)題。同時(shí)，設(shè)計(jì)了觀測(cè)器對(duì)擴(kuò)展?fàn)顟B(tài)進(jìn)行有效估計(jì)。文獻(xiàn)［20-21］中提出了一種基于狀態(tài)觀測(cè)的博弈值函數(shù)近似方法。該方法利用級(jí)數(shù)展開(kāi)對(duì)博弈值函數(shù)進(jìn)行近似，然后通過(guò)觀測(cè)目標(biāo)的狀態(tài)信息對(duì)級(jí)數(shù)的各系數(shù)進(jìn)行更新。該方法具有較高的計(jì)算效率和精度，已經(jīng)在空間攻防任務(wù)中得到了廣泛應(yīng)用。文獻(xiàn)［22-23］中考慮了模型不確定問(wèn)題，首先預(yù)設(shè)了多種攔截彈可能采取的制導(dǎo)率，并設(shè)計(jì)了多個(gè)估計(jì)器并行計(jì)算不同情況下攔截彈的最優(yōu)狀態(tài)估計(jì)，并給出相應(yīng)估計(jì)后驗(yàn)概率。然后，通過(guò)概率融合方法將不同估計(jì)器得到的最優(yōu)狀態(tài)估計(jì)和后驗(yàn)概率融合，得到更加準(zhǔn)確的攔截彈制導(dǎo)率。最后，通過(guò)設(shè)計(jì)目標(biāo)和防御器的協(xié)同制導(dǎo)率有效躲避了攔截。

雖然追逃博弈問(wèn)題已經(jīng)得到了廣泛研究，但大多數(shù)研究都是以攔截器可以完全獲得目標(biāo)信息的假設(shè)為基礎(chǔ)進(jìn)行的，或者是基于簡(jiǎn)化的動(dòng)力學(xué)模型研究不完全信息博弈，這與實(shí)際的航天器追逃博弈態(tài)勢(shì)存在較大差異。因此，本文針對(duì)不完全信息下的航天器追逃博弈問(wèn)題進(jìn)行了研究，實(shí)現(xiàn)了在不完全信息下對(duì)目標(biāo)的快速攔截。隨著低軌目標(biāo)攔截技術(shù)不斷發(fā)展，任務(wù)能夠快速準(zhǔn)確地獲得發(fā)射窗口［24］，該方法也將成為未來(lái)處理一類具備智能體特性的失控航天器的機(jī)動(dòng)策略之一。通過(guò)快速接近不受地面指令控制的失控航天器，并將其引導(dǎo)到安全軌道，可以避免對(duì)其他航天器和空間設(shè)施造成威脅。

綜合前文所述，本文針對(duì)不完全信息下航天器末端追逃博弈問(wèn)題，首先建立了航天器末端攔截動(dòng)力學(xué)模型，并給出了完全信息下的納什均衡策略對(duì)。然后，考慮目標(biāo)控制矩陣信息不完全的情況，設(shè)計(jì)了基于廣義卡爾曼濾波的行為學(xué)習(xí)信息估計(jì)算法，并嚴(yán)格證明了所提出的不完全信息下微分博弈策略對(duì)滿足Epsilon 納什均衡。最后，通過(guò)仿真驗(yàn)證了算法的有效性和攔截的快速性。本策略不僅適用于航天器攔截任務(wù)，還可以作為星群中具備智能體特性的失控航天器的處理方法，具有實(shí)際應(yīng)用價(jià)值。

1 航天器相對(duì)運(yùn)動(dòng)狀態(tài)方程

在航天器末端攔截段，攔截航天器與目標(biāo)航天器的相對(duì)距離遠(yuǎn)小于兩星質(zhì)心到地心的距離，因此在攔截衛(wèi)星附近設(shè)置參考衛(wèi)星O1，P為攔截航天器，如圖1 所示。假設(shè)參考衛(wèi)星運(yùn)行在圓軌道，以參考衛(wèi)星為原點(diǎn)，x軸沿著參考衛(wèi)星地心矢徑方向，z軸沿著軌道角動(dòng)量方向，y軸滿足右手定則，定義虛擬衛(wèi)星軌道坐標(biāo)系O1xyz［25］，在LVLH 坐標(biāo)系下攔截器相對(duì)參考衛(wèi)星的動(dòng)力學(xué)方程可以簡(jiǎn)化為CW方程：

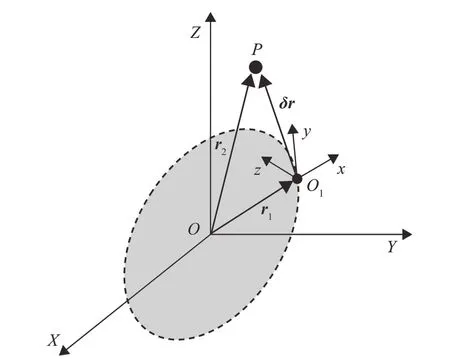
圖1 攔截器與參考衛(wèi)星Fig 1 Interceptor and reference satellite

式中：x，y，z為攔截器相對(duì)參考衛(wèi)星的位置；ω為參考衛(wèi)星的軌道角速度；ux，uy，uz分別為攔截器三軸方向上的控制輸入。

由線性系統(tǒng)理論可得狀態(tài)轉(zhuǎn)移矩陣為：

式中的子矩陣［26］分別為：

式中：τ=t-t0，且滿足(t，t0)=Φ(t，t0)A。

當(dāng)τ=tf-t時(shí)，狀態(tài)轉(zhuǎn)移矩陣Φ滿足(tf，t)=-Φ(tf，t)A。在該虛擬衛(wèi)星軌道坐標(biāo)系下，攔截器與目標(biāo)動(dòng)力學(xué)均滿足CW方程，即：

式中：Ui(i=P，E)分別為攔截器P 以及目標(biāo)E 的推力，且均滿足幅值限制‖UP‖＜ρP，‖UE‖＜ρE。

定義攔截器與目標(biāo)的相對(duì)狀態(tài)為：

對(duì)其求導(dǎo)并將式（4）代入可得相對(duì)狀態(tài)方程：

式中：CE=BP。

2 有限時(shí)間追逃博弈策略對(duì)

在末端博弈過(guò)程中，雙方將圍繞攔截結(jié)束時(shí)的距離展開(kāi)爭(zhēng)奪。攔截器盡可能以最小代價(jià)實(shí)現(xiàn)對(duì)目標(biāo)的快速接近，而目標(biāo)則盡可能以最小代價(jià)增大與攔截器之間的距離。因此，本文定義以下指標(biāo)函數(shù)：

式中：S＞0為對(duì)稱正定矩陣；Q≥0為對(duì)稱半正定矩陣；RP＞0與RE＞0均為對(duì)稱正定矩陣，且滿足：

式中：I∈R3×3為單位陣。

定義如下哈密頓函數(shù)：

式中：λ為協(xié)態(tài)變量。

設(shè)協(xié)態(tài)變量與狀態(tài)變量滿足如下關(guān)系：

式中：P為對(duì)稱正定陣，即P＞0，PT=P。

對(duì)式（12）求導(dǎo)，并將其與式（7）和式（11）代入式（13），可得黎卡提微分方程如式（14）所示。

因此，攔截器與目標(biāo)的鞍點(diǎn)策略對(duì)為：

式中：P滿足式（15），推力滿足幅值限制‖UP‖≤ρP，‖UE‖≤ρE。

3 不完全信息下博弈策略設(shè)計(jì)

本節(jié)考慮攔截航天器無(wú)法獲取目標(biāo)航天器控制矩陣的不完全信息情況。在這種情況下，追逃博弈不再滿足納什均衡，因此本文采用Epsilon 納什均衡（后文簡(jiǎn)寫(xiě)為ε-納什均衡）［27］對(duì)其進(jìn)行描述。此外，目標(biāo)航天器實(shí)際采取式（16）中的博弈策略，掌握著博弈進(jìn)程的完全信息，進(jìn)而獲得更好的逃逸性能。

假設(shè)1.在本節(jié)研究的情境下，攔截器在面對(duì)不完全信息時(shí)存在行為學(xué)習(xí)信息估計(jì)進(jìn)程，而目標(biāo)無(wú)法獲取攔截器的實(shí)際機(jī)動(dòng)策略。

注1.如果目標(biāo)能夠獲取攔截器的實(shí)際策略，那么它將采取誘導(dǎo)策略來(lái)迷惑攔截器，而攔截器則會(huì)采取相應(yīng)的對(duì)策來(lái)應(yīng)對(duì)誘導(dǎo)策略。這種無(wú)限變化的過(guò)程可以被看作是一個(gè)無(wú)限維博弈，因?yàn)殡p方都在不斷地改變自己的策略以適應(yīng)對(duì)方的變化。為了避免這種情況，本文假設(shè)1 指出只有攔截器存在信息估計(jì)的策略，而目標(biāo)不知道該過(guò)程和其實(shí)際機(jī)動(dòng)策略。

定義擴(kuò)展?fàn)顟B(tài)變量Y=[XPETrE]T，則擴(kuò)展?fàn)顟B(tài)方程與量測(cè)方程為：

由于擴(kuò)展?fàn)顟B(tài)方程的非線性，本文采用廣義卡爾曼濾波（類EKF）對(duì)RE進(jìn)行估計(jì)。定義標(biāo)稱狀態(tài)為Yn，Zn，則在標(biāo)稱狀態(tài)點(diǎn)對(duì)式（17）進(jìn)行一階泰勒展開(kāi)可得：

式中：ΔY=Y-Yn，ΔZ=Z-Zn為狀態(tài)偏差，F(xiàn)n為雅克比矩陣，Hn為量測(cè)矩陣，具體形式如下：

式中：Φ(k，k-1)為狀態(tài)轉(zhuǎn)移矩陣，且Φ(k，k-1) ≈I+FnT，Wk-1為過(guò)程噪聲，Vk為量測(cè)噪聲，T為采樣時(shí)間，且滿足如下條件：

式中：Ψk為系統(tǒng)噪聲序列的方差陣，為半正定陣；Rk為量測(cè)噪聲序列的方差陣，為正定陣；δkj為Kronecker符號(hào)。

圖2所示為不完全信息下的博弈控制策略流程，針對(duì)線性化的狀態(tài)方程（21），采用卡爾曼濾波進(jìn)行狀態(tài)估計(jì)，此時(shí)的濾波方程為：

為了盡可能減小狀態(tài)偏差，本文希望狀態(tài)標(biāo)稱值盡可能接近于狀態(tài)最優(yōu)估計(jì)值。因此，可以將狀態(tài)標(biāo)稱值設(shè)置為狀態(tài)最優(yōu)估計(jì)值，以減少估計(jì)誤差。

式中：P*滿足如下黎卡提方程：

且P*仍滿足終端條件P*(tf)=S。

4 滿足ε-納什均衡的數(shù)學(xué)證明

在實(shí)際的空間攻防過(guò)程中，存在許多不確定性因素，例如戰(zhàn)爭(zhēng)迷霧、傳感器約束、目標(biāo)無(wú)規(guī)律機(jī)動(dòng)等。這些因素導(dǎo)致了目標(biāo)信息的不完全性，從而無(wú)法滿足完全信息下的納什均衡，因此完全信息策略不再適用。本節(jié)將嚴(yán)格證明所設(shè)計(jì)的微分博弈策略對(duì)滿足ε-納什均衡。這意味著，當(dāng)策略對(duì)滿足更加寬松的ε-納什均衡時(shí)，可以確保攔截航天器處在不完全信息下的最劣情況時(shí)仍能獲得近似最優(yōu)解，并且目標(biāo)航天器的機(jī)動(dòng)策略不會(huì)對(duì)其收益帶來(lái)較大影響。

定理1.設(shè)攔截航天器與目標(biāo)航天器的動(dòng)力學(xué)方程為式（7），指標(biāo)函數(shù)采用式（8），攔截器實(shí)際采取的策略為式（25），記為，目標(biāo)實(shí)際采取的策略為式（16），記為。此時(shí)博弈策略對(duì)形成ε-納什均衡，即：

證.采取狀態(tài)估計(jì)策略下，相應(yīng)的航天器狀態(tài)分別記為，協(xié)態(tài)變量記為λ*，此時(shí)的博弈策略對(duì)改寫(xiě)為：

將式（29）代入相對(duì)狀態(tài)方程（7），并積分可得：

此時(shí)的指標(biāo)函數(shù)為：

注2.當(dāng)攔截器采取不同的機(jī)動(dòng)策略時(shí)，會(huì)導(dǎo)致兩者相對(duì)狀態(tài)變量的不同，因此盡管目標(biāo)都采取了最優(yōu)策略，但是對(duì)應(yīng)的控制輸入?yún)s可能是不同的。綜上所述，本文將這種情況下的目標(biāo)策略記為。

此時(shí)的狀態(tài)變量為：

此時(shí)的指標(biāo)函數(shù)為：

同時(shí)，對(duì)式（13）進(jìn)行積分，并結(jié)合橫截條件可得：

式中：i為任意策略。

定義狀態(tài)變量差為ΔX=X*-X+，協(xié)態(tài)變量差為Δλ=λ*-λ+，分別將式（30）、（33）和（35）代入得到：

對(duì)上式中的ΔXT(tf)SX+(tf)項(xiàng)進(jìn)行積分變換，則有：

令τ1-t0=τ-tf，則有：

式中：λmax(·)表示矩陣的最大特征值，由函數(shù)積分有界性定理可知：

因此，不完全信息下的追逃博弈策略設(shè)計(jì)滿足ε-納什均衡。

5 仿真校驗(yàn)

為了驗(yàn)證所提出的行為學(xué)習(xí)信息估計(jì)追逃博弈策略在不完全信息條件下的有效性，本節(jié)進(jìn)行了3 種不同情況的對(duì)比分析，包括完全信息、不完全信息和不完全信息條件下的信息估計(jì)博弈策略。

在完全信息條件下，假設(shè)雙方都可以獲取對(duì)方采取的納什均衡策略和當(dāng)前狀態(tài)信息。而在不完全信息條件下，假設(shè)攔截器只獲取到初始位置和對(duì)方可能采取的策略集合。在信息估計(jì)博弈條件下，本文考慮實(shí)際空間攻防中末端追逃場(chǎng)景，采用提出的不完全信息下ε-納什均衡博弈策略追擊目標(biāo)。通過(guò)對(duì)比分析3 種不同條件下的末端追逃結(jié)果，本節(jié)評(píng)估了所提出的不完全信息ε-納什均衡的航天器追逃博弈策略的有效性。

初始條件設(shè)定如下：假設(shè)攔截航天器與目標(biāo)均運(yùn)行在近地軌道附近，選取近地軌道上與其相近的衛(wèi)星作為參考衛(wèi)星，其軌道角速度ω=0.001 rad · s-1。攔截器與目標(biāo)的初始位置分別為[1.5 0.5 0]Tkm，[0 0 0]Tkm，初始速度分別為[0 0 0]Tkm · s-1，[ -0.05 0 0.05]Tkm · s-1。

假設(shè)攔截器與目標(biāo)的最大推力加速度均為10 m·s-2，廣義Kalman 濾波中過(guò)程噪聲方差陣為diag[10-610-610-60.25 × 10-60.25 × 10-60.25 × 10-61010]，量測(cè)噪聲方差陣為diag[10-810-810-80.25 ×10-80.25 × 10-80.25 × 10-8]。

5.1 完全信息博弈

在這種情況下，攔截器可以精確獲取到目標(biāo)的控制矩陣RE。通過(guò)仿真，可以觀察到圖3和圖4中展示的航天器三維運(yùn)動(dòng)軌跡和相對(duì)距離變化，在488 s時(shí)，攔截器成功地?cái)r截了目標(biāo)。此外，圖5展示了完全信息博弈進(jìn)程中攔截器的控制加速度變化情況。

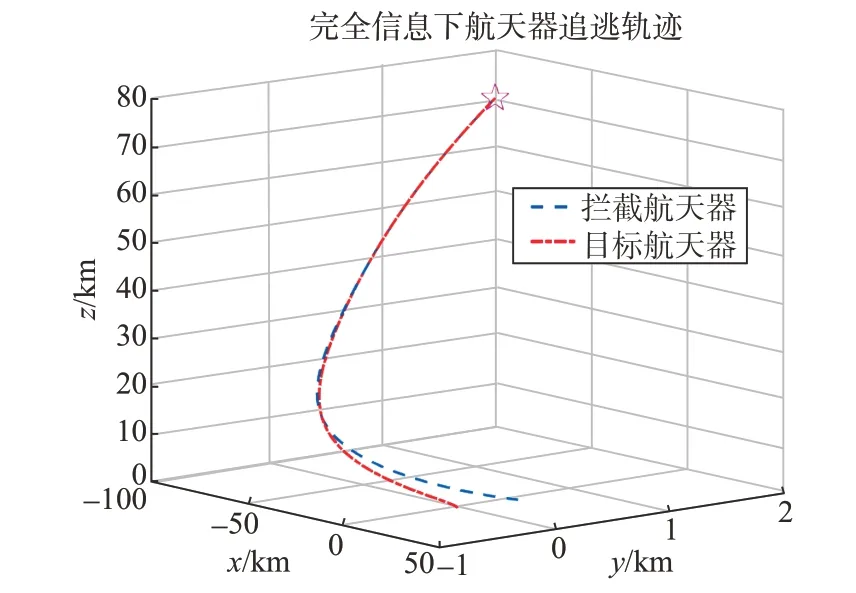
圖3 完全信息下航天器追逃軌跡Fig.3 Spacecraft pursuit-evasion trajectory under complete information

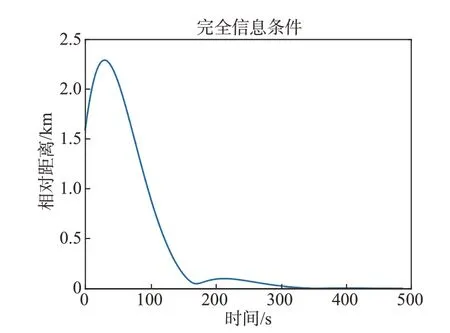
圖4 完全信息下航天器相對(duì)距離Fig.4 Relative distance of spacecraft under complete information

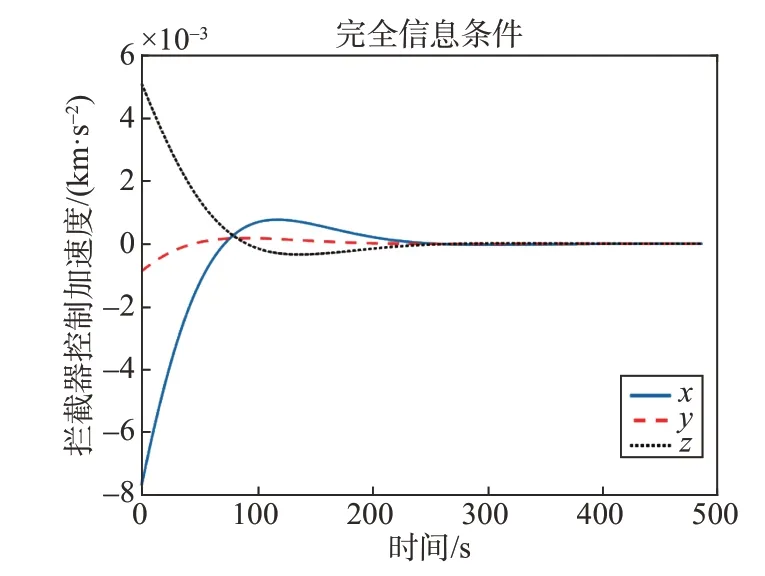
圖5 完全信息下攔截器控制加速度Fig.5 Control acceleration of the interceptor under complete information

5.2 不完全信息博弈

在這種情況下，攔截器無(wú)法準(zhǔn)確獲取到目標(biāo)的控制矩陣，只能通過(guò)猜測(cè)該矩陣來(lái)設(shè)計(jì)攔截器策略，假設(shè)攔截器猜測(cè)的目標(biāo)控制矩陣為=2 ×106I3。

通過(guò)仿真圖6 可以看出航天器間追逃軌跡，且攔截器在1 979 s 時(shí)成功攔截了目標(biāo)。然而，從圖7中可以看出，攔截器與目標(biāo)的相對(duì)距離變化很劇烈，經(jīng)過(guò)多次震蕩，攔截器才最終實(shí)現(xiàn)攔截。

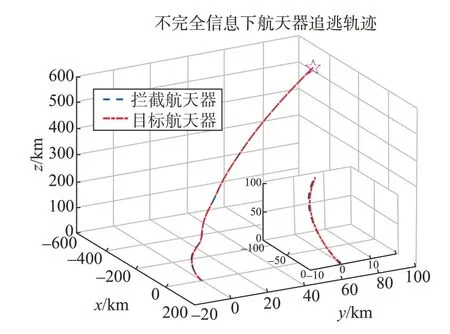
圖6 不完全信息下航天器追逃軌跡Fig.6 Spacecraft pursuit-evasion trajectory under incomplete information

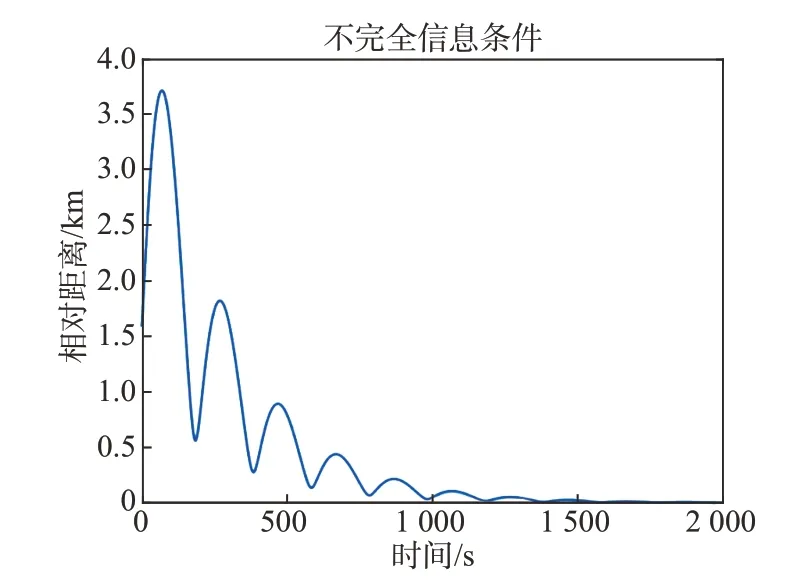
圖7 不完全信息下航天器相對(duì)距離Fig.7 Relative distance of spacecraft under incomplete information

通過(guò)比較圖5 和圖8 可以看出，由于攔截器是在猜測(cè)較大的值下決策的，該條件下的控制加速度表現(xiàn)出劇烈的振蕩，攔截過(guò)程的控制性能顯著下降。仿真結(jié)果表明，如果攔截器不能完全獲得目標(biāo)的信息，會(huì)導(dǎo)致攔截時(shí)間增加、攔截性能下降。因此，在航天器追逃控制中，對(duì)目標(biāo)的不完全信息進(jìn)行估計(jì)具有重要意義。

5.3 不完全信息下信息估計(jì)博弈策略

在這種情況下，攔截器采用信息估計(jì)的方法來(lái)適配目標(biāo)的控制矩陣，從而建立不完全信息下的博弈策略。假設(shè)攔截器對(duì)目標(biāo)控制矩陣的初始估計(jì)值為=2 × 106I3。

通過(guò)圖9和圖10可以觀察到航天器的三維追逃軌跡以及兩者間相對(duì)距離的變化情況，攔截器在經(jīng)過(guò)501 s 的追擊后成功地?cái)r截了目標(biāo)。從仿真圖11中可以看出，在估計(jì)目標(biāo)控制矩陣并采取相應(yīng)的行為學(xué)習(xí)方法后，攔截器的控制性能與完全信息條件下的情況相對(duì)接近，說(shuō)明在目標(biāo)信息不完全的情況下，通過(guò)信息估計(jì)來(lái)適配目標(biāo)的控制矩陣可以有效提高航天器的攔截性能。

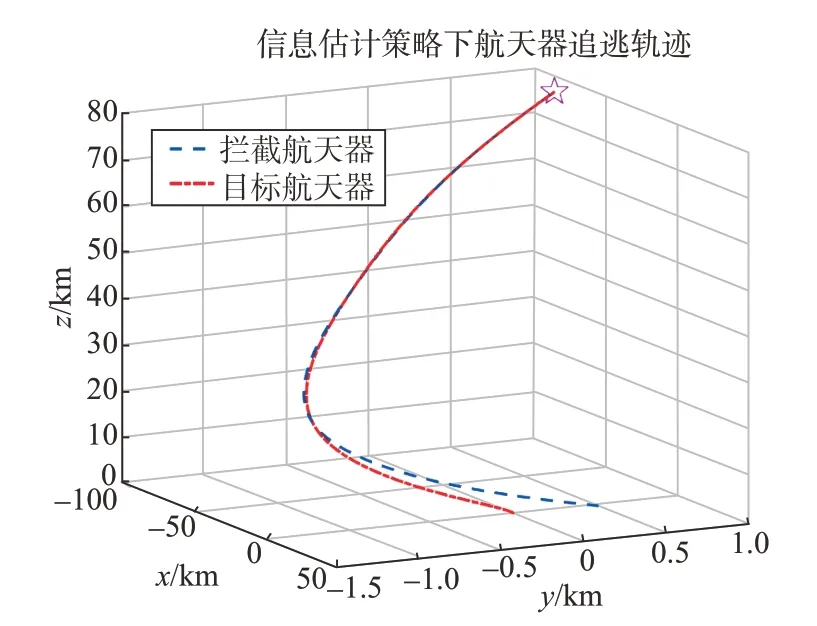
圖9 不完全信息估計(jì)策略下航天器追逃軌跡Fig.9 Spacecraft pursuit-evasion trajectory under estimation strategy

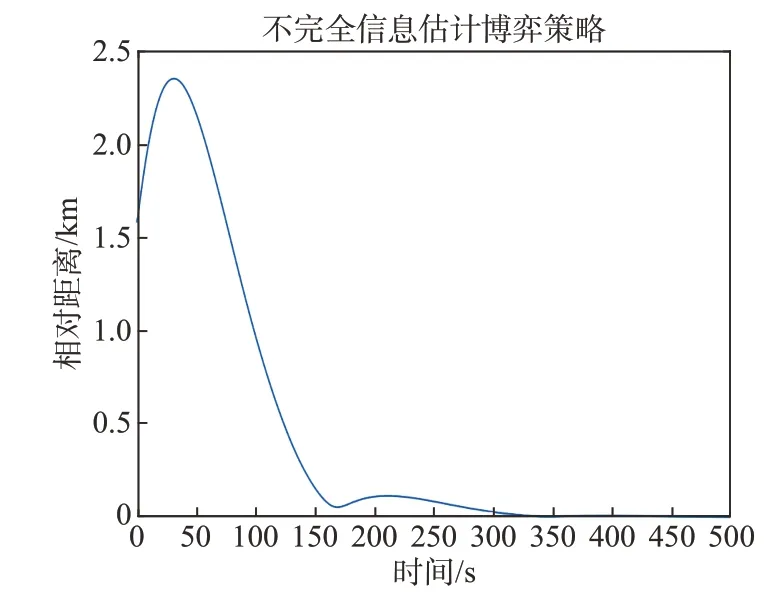
圖10 不完全信息估計(jì)策略下航天器相對(duì)距離Fig.10 Relative distance of spacecraft under estimation strategy

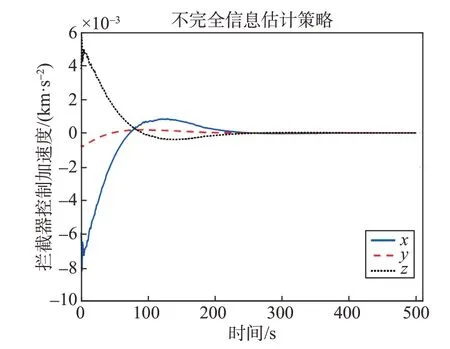
圖11 不完全信息估計(jì)策略下攔截器控制加速度Fig.11 Control acceleration of the interceptor under estimation strategy

圖12 顯示了攔截器對(duì)目標(biāo)控制矩陣信息的估計(jì)誤差，通過(guò)廣義Kalman 濾波算法，可以有效地對(duì)目標(biāo)信息進(jìn)行估計(jì)，估計(jì)誤差快速收斂。

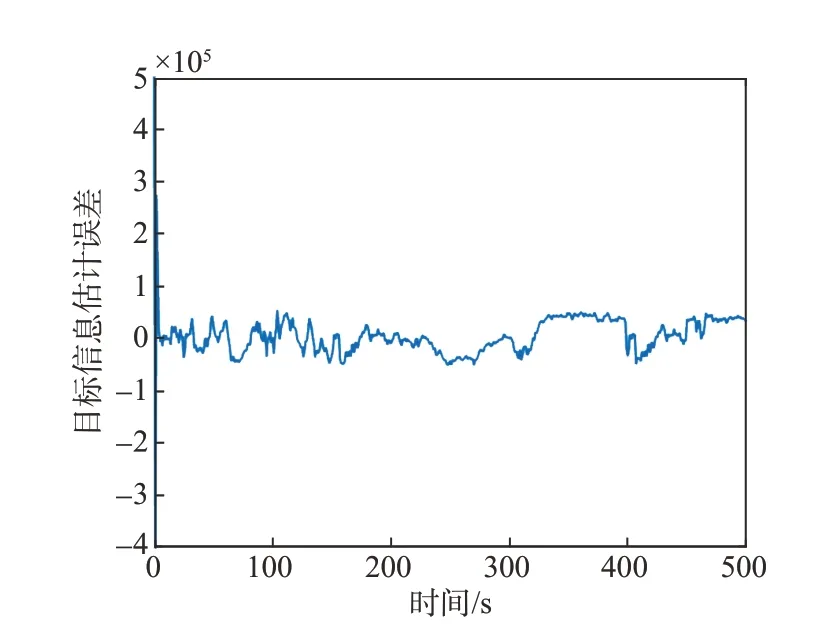
圖12 目標(biāo)信息估計(jì)誤差Fig.12 Estimation error of the target information

在追逃博弈中，代價(jià)函數(shù)值是衡量策略優(yōu)劣的標(biāo)準(zhǔn)。圖13 給出了3 種博弈場(chǎng)景的代價(jià)函數(shù)指標(biāo)。結(jié)果表明，當(dāng)攔截器采用信息估計(jì)策略時(shí)，相應(yīng)的指標(biāo)明顯優(yōu)于不完全信息方案，攔截時(shí)間短、成本低，并且接近完全信息方案的指標(biāo)，這驗(yàn)證了不完全信息估計(jì)博弈策略的有效性。

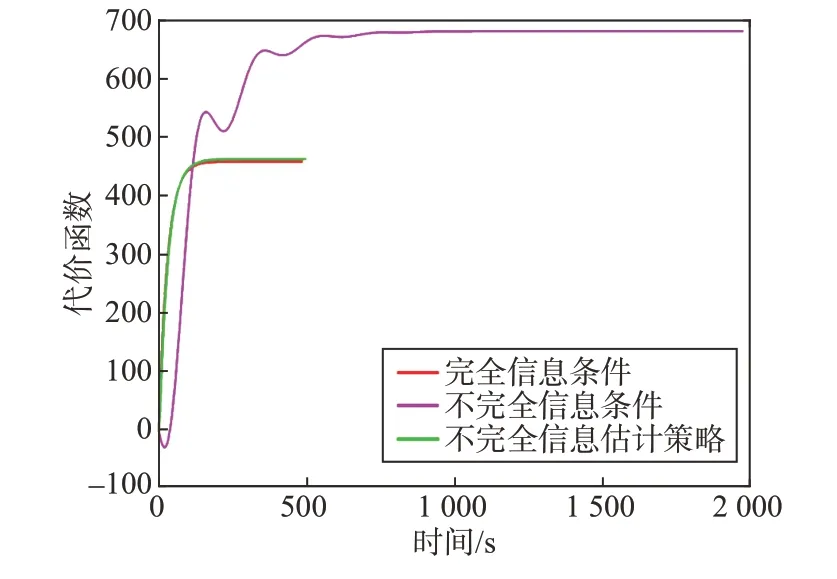
圖13 三種博弈場(chǎng)景的代價(jià)函數(shù)指標(biāo)值Fig.13 The cost function values of the three game scenarios

6 結(jié)論

本文探討了在不完全信息的情況下，如何設(shè)計(jì)一種快速、有效的航天器末端追逃博弈策略。首先，本文基于微分對(duì)策理論推導(dǎo)出完全信息下的納什均衡策略對(duì)。為了對(duì)未知的目標(biāo)信息進(jìn)行估計(jì)，進(jìn)一步提出了基于廣義Kalman 濾波的估計(jì)算法。在此基礎(chǔ)上，設(shè)計(jì)了不完全信息下的航天器追逃博弈策略，并嚴(yán)格證明了該策略滿足ε-納什均衡條件。最后，通過(guò)仿真分析驗(yàn)證了該策略的有效性，結(jié)果表明采用本文提出的末端追逃博弈策略可以有效地估計(jì)目標(biāo)信息并實(shí)現(xiàn)快速攔截。

綜上所述，博弈論與空間飛行器導(dǎo)航、制導(dǎo)與控制相結(jié)合具有廣闊的應(yīng)用前景，能夠?yàn)槲磥?lái)具有自主避障能力的航天器攔截領(lǐng)域研究提供新的思路和方法，有望成為未來(lái)空間攻防任務(wù)的重要突破點(diǎn)。