先行組織促遷移,動點距離探最值

華南師范大學數學科學學院(510630) 黃雅萱 梁鈺清

廣州市白云區白云實驗學校(510080) 黃詩韻

1 先行組織者

先行組織者由奧蘇伯爾提出,是學習新知識材料時呈現一種起組織作用、抽象概括程度較高的材料;是把新內容與學生已有的知識聯系起來,幫助學生組織要學習的材料.先行組織者分為陳述性與比較性,陳述性組織者主要通過定義和概括進行,用于較陌生的學習材料,即向學生呈現概括性水平高于新知的材料,讓學生獲得同化新知識的框架.比較性組織者主要通過類推進行,用于較熟悉的學習材料中,即當學生面對新的學習任務時,倘若其認知結構中已經具有了可以利用的同化新知識的適當觀念,但原有觀念不清晰或不穩定,學生難以應用,或者他們對新舊知識之間的關系辨別不清,則可以設計一個揭示新舊知識異同的比較性組織者.通過在數學課堂中呈現比較性先行組織材料,能夠將學生認知結構中的某類知識與新知識進行類推,增強新舊知識之間的可辨別性,幫助學生明晰新舊知識的關系[1].

2 先行組織者在教學中的應用案例

2.1 運用先行組織者策略的內容解析

兩條平行線之間的距離的定義以及性質在教材中是由平行四邊形的性質引出,選自人教版《義務教育課程標準實驗教科書·數學》八年級下冊的18.1 節.

點到直線的距離(以下簡稱點線距離)是一個定點與在一條直線上的動點之間的距離問題,兩條平行線之間的距離(以下簡稱線線距離)是平行線間兩個動點之間的距離問題——即點線距離和線線距離的本質是兩點之間的距離(以下簡稱點點距離).換言之,點點距離是點線距離、線線距離的“比較性先行組織材料”.課例創設“鄉村振興”主題情境,在情境中以問題串引導學生明確三種距離本質上都是點點距離,搭建先行組織者與新知材料的關系(見圖1).最后,動點間距離的最值問題是新學習材料的一個直接應用,要求學生扎實掌握新知識的特征,并明晰新學習材料的本質后,從題目條件中抽象出新學習材料的特征結構,從而轉化問題,進行求解.

圖1 先行組織者策略運用思路

2.2 教學目標與重難點分析

(1)理解線線距離的概念;了解線線距離和點點之間的距離、點線的距離的聯系;

(2)通過從先行組織材料中得到新知的方式培養學生遷移的能力,在經歷將實際問題轉化為數學問題的過程中體會轉化思想;在利用線線距離的知識解決最值問題中發展推理能力;

(3)運用數學知識解決鄉村振興問題,激發數學學習積極性,產生利用知識回報鄉村的積極想法.從解決數學問題的過程中,感悟數學來源于生活、運用于生活.

“距離”是初中數學中重要的知識,在最短路徑等最值問題中具有重要的價值,且作為初高中銜接的一個重要內容,扎實掌握距離的相關知識對于高中距離的進一步學習具有重要鋪墊作用.在學習“線線距離”時,學生對于距離的學習過去了一年,且是結合平行四邊形給出線線距離的概念,對學生的知識遷移能力要求較高.為此,依托先行組織者策略整合教材內容,讓學生理解平行線間距離是教學重點之一,同時,線線距離的應用——動點間距離最值問題是本節教學的另一個重難點,以多個變式引導學生探究如何分析條件轉化最值問題,培養學生解決一類最值問題的能力,啟發思維.

2.3 教學片斷

(1)情境引入,初探新知

情境創設:為響應鄉村振興的號召,干部深入基層運用專業知識支援鄉村發展.2022 年修建了旅游公路,其中旅游公路與田地垂直而建.為充分利用村里的土地,提高經濟效益,干部和村長敲定種植出品馬鈴薯和油菜等農產品.但是馬鈴薯和油菜是需水量較大的農作物,還需要引渠灌溉.農田附近有一條河流,此河流恰與旅游公路垂直(如圖1).為節約成本,如何修建水渠才能最短? 你能幫助德美村解決這個問題嗎?

問題1:河流和農田有何種位置關系?

師生活動:教師用手勢比劃河岸及農田與旅游公路的關系,學生觀察教師動作、結合情境,回答農田與河流都與旅游公路垂直,可以將農田與河流看作一組平行線(如圖2).

圖1

追問:同學們可以將“如何修建水渠才能最短”這一實際問題轉化為數學問題嗎?

生1:在一組平行線之間連線,其中哪一條最短? (如圖3)

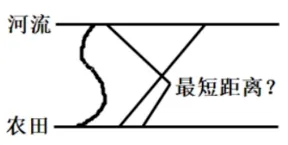
圖3

設計意圖《全日制義務教育數學課程標準》強調要讓學生經歷現實情境的水平數學化[2],本環節以鄉村振興為背景創設情境,一方面引出數學問題,學生提高水平數學化能力,另一方面滲透振興鄉村的思想,加強學生的德育教育.

(2)知識串聯,同化建構

師生活動:教師用手勢比劃兩條平行線上不同位置,語言強調在兩條平行線上任意取1 點連線,學生觀察教師動作,感受“在一組平行線之間連線,其中哪一條最短? ”這一問題的本質是“在平行線上的兩動點間連線,哪條線最短? ”

問題2:如圖4,三種連線方式,哪種連線方式長度最短?

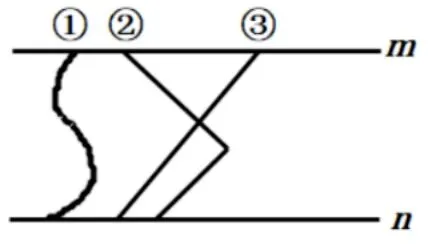
圖4

生2:方案③最短,因為兩點之間,線段最短.

問題3:平行線上有無數個點,分別選取哪兩點連線段,才能使線段最短呢?

學生思考并未回答問題.

追問:同時考慮兩條平行線上的2 個動點很困難,可否先固定其中一點呢? 如圖5,在直線m上選定一點P,請在直線n上確定一點,使得兩點連線最短.

圖5

學生活動:學生發現這是點到直線的最短距離問題,所以過點P作關于直線n的垂線段,此時點P到直線n的距離最短(如圖6).

圖6

追問:如圖7,在直線m再取一點E,向直線n作垂線段,那么PQ=EF嗎? 如何證明?

圖7

師生活動:大部分學生猜測PQ=EF,接下來教師引導學生利用平行四邊形的判定與性質定理完成證明.

追問:我們利用兩條垂線段平行的條件,利用平行四邊形的判定及性質定理證明了在兩條平行線間,垂線段互相平行且相等.那么在兩條平行線間,任意一組平行線段長度相等嗎?

學生集體回答相等,運用同樣的方法可以證明.

師:通過以上的證明,我們知道平行線間任意一組平行線段長度相等.那么在無數組長度相等的平行線段中,哪一組線段最短呢?

生3:垂線段是最短的,因為在平行線上任意選一點,向另一條平行線作垂線段最短.

師:沒錯! 在無數組長度相等的平行線段中,垂線段最短.

設計意圖通過手勢與語言強調讓學生感受線線距離的本質是平行線間兩個動點之間的距離問題,再進一步引導學生將兩個動點點間的距離問題轉化為一個定點與在一條直線上的動點之間的距離問題——在此過程中,呈現點點距離和點線距離這一比較性先行組織材料,循序漸進引導學生在比較性先行組織材料(點點距離、點線距離)與新知(線線距離)之間建立遷移橋梁,有助于學生明晰線線距離與點點距離、點線距離的關系.

(3)知識生成,鞏固升華

教師活動:根據以上探究過程,教師闡述兩條平行線間的距離的定義.

定義:兩條平行線中,一條直線上任意一點到另一條直線的距離,叫做兩條平行線之間的距離.

師生活動:根據環節三得到的結論,教師引導學生表述平行線間距離處處相等的性質及命題.

命題1:兩條直線平行,那么一條直線上所有的點到另一條直線的距離都相等.

命題2:兩條直線平行,一條直線上任一點到另一條直線的距離,為兩條平行線之間的最短距離.

問題4:請同學們利用數學知識,設計一個建渠方案.

學生們回答在河岸上取若干灌水點,向農田作垂直于農田水渠.

師生活動:回顧建造水渠中問題轉化的過程,歸納點點距離、點線距離與線線距離的關系,如圖8.

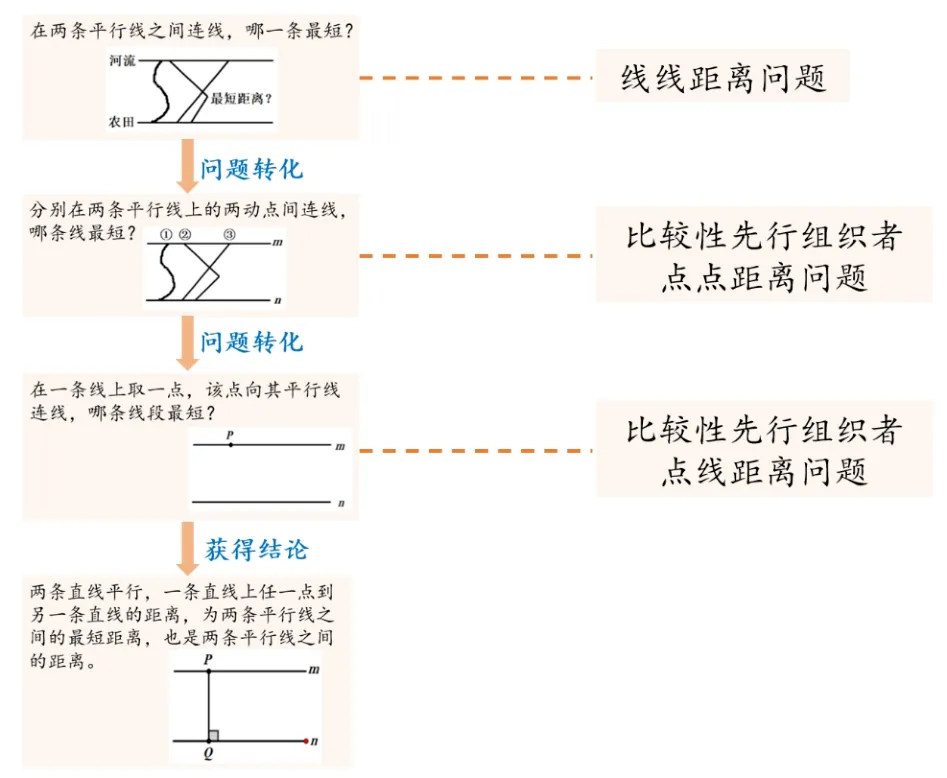
圖8

圖9

設計意圖基于前三個環節的鋪墊,學生基于“點點距離”、“點線距離”等比較性先行組織材料,經歷了知識的同化與建構,此環節總結習得的定義及命題、闡述點點距離、點線距離和線線距離的關系,加深對平行線之間距離的意義的理解,達到教學目標,突破教學重難點.

(4)知識應用,拾級而上

以本道例題作為變式的基礎,該題是線線距離的定義和性質的直接應用,學生初步感知線線距離在最值問題中的應用.

變式1:如圖10,在RtΔABC中,∠B=90°,AB=4,BC＞AB,點D在BC上,四邊形ADCE是以AC為對角線的平行四邊形,求DE的最小值.

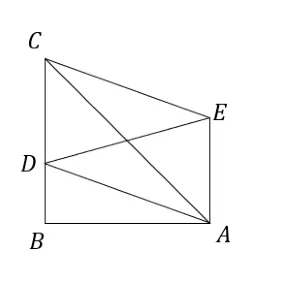
圖10

此題以平行四邊形提供一組平行線,已知D點是動點,題目條件以AC為對角線構造平行四邊形,隱含著的E點是平行線上的一個動點,即通過構造圖形給出一個隱含條件,教師引導學生外顯隱形條件后直接利用性質解題.

變式2:如圖11,在菱形ABCD中,AB=4,點P、M、N分別是BC、AC、AB邊上的動點,求PM+MN的最小值.

圖11

首先運用“將軍飲馬”將線段和最值轉化為一條線段的最值,由于菱形的性質,轉化后,線段兩端點恰在菱形的一組平行對邊上,通過一次轉化,一個隱含條件將問題轉化為平行線上動點間距離最值問題,從而利用性質解題.

變式3:如圖12,在RtΔABC中,∠C=90°,AB=點E、F分別是線段BC、AC上一動點,運動過程中保持FA=FD、ED=EB,G為AD中點,求EF的最小值.

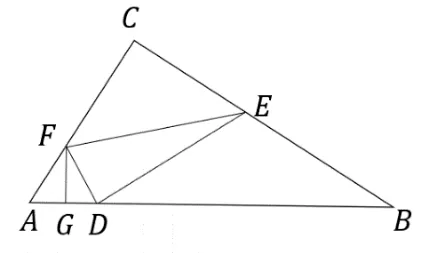
圖12

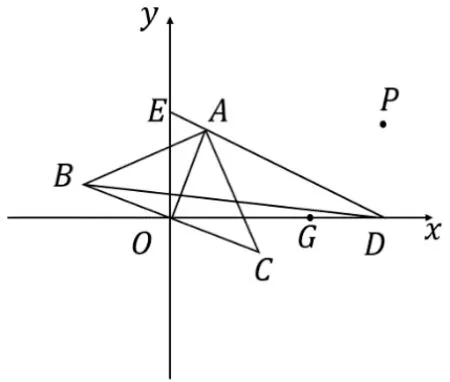
圖13

首先分析題目,由FA=FD、ED=EB得到兩個等腰三角形,根據“三線合一”,過E點作AB的垂線,這是第一次轉化,也是兩條平行線的隱含條件——兩條垂線平行,兩條運動的平行線始終是由兩動點E,F引出,這是動態中蘊含的靜態轉化,最后將問題轉化為兩條運動的平行線間的最短距離問題,通過“三線合一”再次轉化,得到最短距離與AB的關系.

變式4:如圖,等腰直角三角形ABC的斜邊BC的中點與坐標原點重合,D(6,0),G點是OD上的一個動點,已知SΔABD=18,AC平分∠OAD,若P點是一個與A點縱坐標相等的動點,求PG的最小值.

本題首先根據P點與A點縱坐標相同,連接PA可得PA//OD,由此將PG最值轉化為平行線間最短距離,接著,如何求解兩平行線間的距離呢? 引導學生發現由等腰直角三角形和角平分線可以推出∠CAD=∠ACB,由“內錯角相等,兩直線平行”得BC//AD.教師再引導學生依據平行線間距離處處相等的性質,進行等面積轉化,得到SΔABD=SΔAOD,由此結合D點坐標可以求得A到OD的距離,即為平行線AP與OD間的距離.

設計意圖距離最短問題是初中幾何中常見的幾何類型,這些問題最終都會轉化為“兩點之間,線段最短”或“垂線段最短”.特別的,平行線上兩動點之間距離最短問題是其中一類重要的題型,也是本課例的教學重點之一.本環節旨在以多個變式層層遞進,不斷減少顯性條件,增強綜合性,強化學生從條件中識別出平行線上動點間距離問題的能力,提高學生解決此類最值問題的能力.

3 教學反思

3.1 符合認知規律,突破教學難點

奧蘇伯爾說:“影響學習的唯一的最重要的因素是學習者已經知道了什么.”本課例中以先行組織者為教學策略、以鄉村振興為教育背景,進行“平行線間的距離”的教學;并以例題為基礎,精心編制層層遞進的變式,讓學生鞏固習得的“新材料”,培養學生解決最值問題的能力.課例采取的先行組織者策略,以比較性先行組織材料類推新知,關聯知識,促進學生的遷移,符合學生從舊知到新知的認知遷移過程,突破了三種距離問題關系難以明確的教學難點,也克服了學生長久未接觸距離問題而生疏的認知困難.

3.2 增強解決距離最值問題能力

本課例的教學重點之一是線線距離的最值問題探究,四個變式,不斷減少顯性條件,添加知識點,變式2 到變式4 分別利用將軍飲馬、等腰三角形、坐標系三個其他知識進行轉化,最后一個變式更是利用平行線間距離處處相等的性質進行求解.學生通過不同條件下尋找平行線上兩動點距離的幾何模式,不斷強化識別該類模式的能力,增強一類最值問題的解題能力,在課后距離最值問題的作業中完成情況良好,學生反應本節變式的探究讓其腦海中擁有了平行線上動點距離模式,在課后練習中能夠從不同幾何背景中較快地尋找該模式解決問題.