非對(duì)稱集中荷載下無腹筋RC 梁受剪性能試驗(yàn)研究

袁健，劉家棟，段紹偉

（中南林業(yè)科技大學(xué) 土木工程學(xué)院，湖南 長沙 410004）

非對(duì)稱集中荷載作用下的鋼筋混凝土簡(jiǎn)支梁，同一根梁中存在兩個(gè)不同的剪跨比.其中，小剪跨段分擔(dān)的剪力作用較大并具有較高的受剪承載力，大剪跨段受剪承載力較低且剪力作用較小.Brown 等［11］開展了非對(duì)稱集中荷載作用下4 根鋼筋混凝土有腹筋簡(jiǎn)支梁剪切破壞試驗(yàn)，每根梁的小剪跨比為1.7，大剪跨比取值范圍為3.0～5.8.當(dāng)梁中兩個(gè)剪跨比分別為1.7 和5.8 時(shí)，小剪跨段分擔(dān)的剪力是大剪跨段的3.4 倍.作者預(yù)估該梁在小剪跨段發(fā)生剪切破壞，而試驗(yàn)結(jié)果卻恰恰相反.此外，其余3 根梁也均在大剪跨段發(fā)生剪切破壞.由此可見，盡管小剪跨段承擔(dān)的剪力較大，但以混凝土斜壓桿傳遞剪力的方式會(huì)使小剪跨段具有更高的承載力.然而，梁中各剪跨段受剪承載力與剪力作用之間的相對(duì)大小存在不確定性，發(fā)生剪切破壞的位置尚不明晰，相關(guān)試驗(yàn)研究也鮮見報(bào)道.

Brown 等的試驗(yàn)研究中箍筋作用與剪跨比兩個(gè)影響因素交織在一起，在一定程度上不利于直觀地揭示問題的本質(zhì).為此，本文開展6 根非對(duì)稱和4 根對(duì)稱集中荷載作用下鋼筋混凝土無腹筋簡(jiǎn)支梁的受剪性能試驗(yàn)研究，并分析GB 50010—2010、修正壓力場(chǎng)理論（簡(jiǎn)稱“MCFT 公式”）［12-13］、基于截面應(yīng)變分析的抗剪模型（簡(jiǎn)稱“Choi 公式”）［14-15］和Zsutty 統(tǒng)計(jì)公式的適用性.

1 試驗(yàn)概述

1.1 試件設(shè)計(jì)

本試驗(yàn)共設(shè)計(jì)10 根鋼筋混凝土無腹筋簡(jiǎn)支梁試件，梁截面尺寸均為200 mm×400 mm，截面有效高度為360 mm.梁底部配置3 根直徑為22 mm 的HRB400 級(jí)縱向受拉鋼筋，配筋率為1.58%.其中，6根梁采用非對(duì)稱加載方式，4根梁在跨中施加集中荷載作為對(duì)比.為加強(qiáng)梁端縱筋的錨固效果，所有試件的縱筋在支座以外彎起并配置箍筋.試件的具體設(shè)計(jì)參數(shù)見圖1和表1.表1中，基于梁的極限承載力試驗(yàn)值Pu，利用力學(xué)平衡關(guān)系計(jì)算得到大、小剪跨段承擔(dān)的剪力分別為VW和VE.

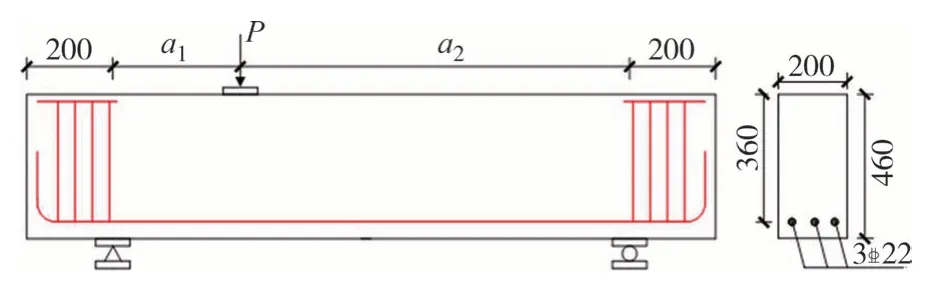
圖1 試件截面尺寸及配筋（單位：mm）Fig.1 Cross-sectional size and reinforcement of specimens（unit：mm）

1.2 材性試驗(yàn)

為了盡可能保證所有試件的混凝土強(qiáng)度相同，采用強(qiáng)度等級(jí)為C35 的商品混凝土，粗骨料最大粒徑為26.5 mm.澆筑試件過程中，制作12 個(gè)邊長為150 mm 的混凝土立方體試塊，并與試件同條件養(yǎng)護(hù)至試驗(yàn)階段.按照《混凝土物理力學(xué)性能試驗(yàn)方法標(biāo)準(zhǔn)》（GB/T 50081—2019）［16］的規(guī)定，以0.5 MPa/s的加載速率實(shí)測(cè)得到混凝土立方體抗壓強(qiáng)度平均值fcu，m=42.8 MPa.采用《混凝土強(qiáng)度檢驗(yàn)評(píng)定標(biāo)準(zhǔn)》（GB/T 50107—2010）［17］的非統(tǒng)計(jì)方法進(jìn)行評(píng)定，可取混凝土立方體抗壓強(qiáng)度的標(biāo)準(zhǔn)值為37.2 MPa，將其代入GB 50010—2010 中相關(guān)公式可計(jì)算得到混凝土的彈性模量Ec=3.19 × 104N/mm2.按照《金屬材料拉伸試驗(yàn) 第1部分：室溫試驗(yàn)方法》（GB/T 228.1—2010）［18］的相關(guān)規(guī)定，實(shí)測(cè)得到縱向受拉鋼筋的屈服強(qiáng)度為422 MPa.根據(jù)GB 50010—2010 取鋼筋的彈性模量Es=2.0 × 105N/mm2，計(jì)算得到相應(yīng)的屈服應(yīng)變?yōu)? 110 με.

1.3 加載方式和測(cè)量?jī)?nèi)容

試驗(yàn)采用液壓千斤頂施加集中荷載，AB 系列試件加載點(diǎn)位于試件跨中偏東，B 系列試件加載點(diǎn)位于試件的跨中處，加載裝置示意圖如圖2 所示.其中，加載點(diǎn)處鋼墊塊及支座寬度均為80 mm.需要說明的是，本文確定剪跨比時(shí)未考慮鋼墊塊及支座寬度的影響.試驗(yàn)前進(jìn)行預(yù)加載，檢查各采集儀器是否正常工作.正式加載過程中，根據(jù)預(yù)估破壞荷載進(jìn)行分級(jí)加載，每級(jí)荷載增量為預(yù)估破壞荷載的1/10；完成加載后持荷5 min，及時(shí)描繪裂縫、量測(cè)裂縫寬度并記錄數(shù)據(jù)；接近破壞時(shí)，每級(jí)荷載增量調(diào)整為5 kN，加載直至試件破壞.

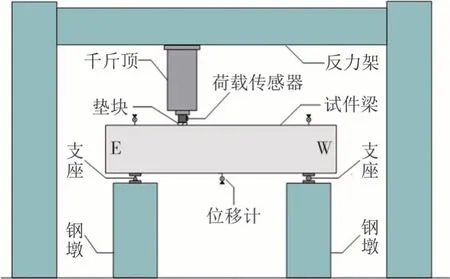
圖2 試驗(yàn)裝置示意圖Fig.2 Schematic diagram of test set-up

在跨中和支座處布置數(shù)顯位移計(jì)，用于測(cè)量梁跨中處的位移及支座處的沉降.千斤頂施加的荷載直接通過壓力傳感器讀取，并采用DH3821靜態(tài)應(yīng)變儀采集應(yīng)變數(shù)據(jù).縱向受拉鋼筋表面應(yīng)變片的布置情況，如圖3所示.

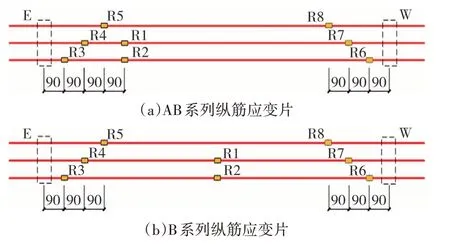
圖3 縱向受拉鋼筋應(yīng)變測(cè)點(diǎn)布置（單位：mm）Fig.3 Layout of strain measuring points for longitudinal tensile reinforcement（unit：mm）

2 試驗(yàn)結(jié)果及分析

2.1 破壞形態(tài)

試件破壞形態(tài)如圖4所示，主要試驗(yàn)結(jié)果見表1.其中，參照文獻(xiàn)［19］判定試件AB1.0-1.5發(fā)生了混凝土劈裂破壞；試件AB1.0-3.5、AB1.0-4.0 和B-3.0 發(fā)生斜拉破壞，而其余試件發(fā)生剪壓破壞.

實(shí)時(shí)數(shù)據(jù)庫是MCGS應(yīng)用系統(tǒng)的數(shù)據(jù)處理中心。系統(tǒng)各個(gè)部分均以實(shí)時(shí)數(shù)據(jù)庫為公用區(qū)交換數(shù)據(jù)，實(shí)現(xiàn)各個(gè)部分協(xié)調(diào)動(dòng)作。在本項(xiàng)目中，實(shí)時(shí)數(shù)據(jù)庫中主要包括狀態(tài)監(jiān)控和參數(shù)設(shè)置兩大類，需要將所有用到的數(shù)據(jù)創(chuàng)建出來。

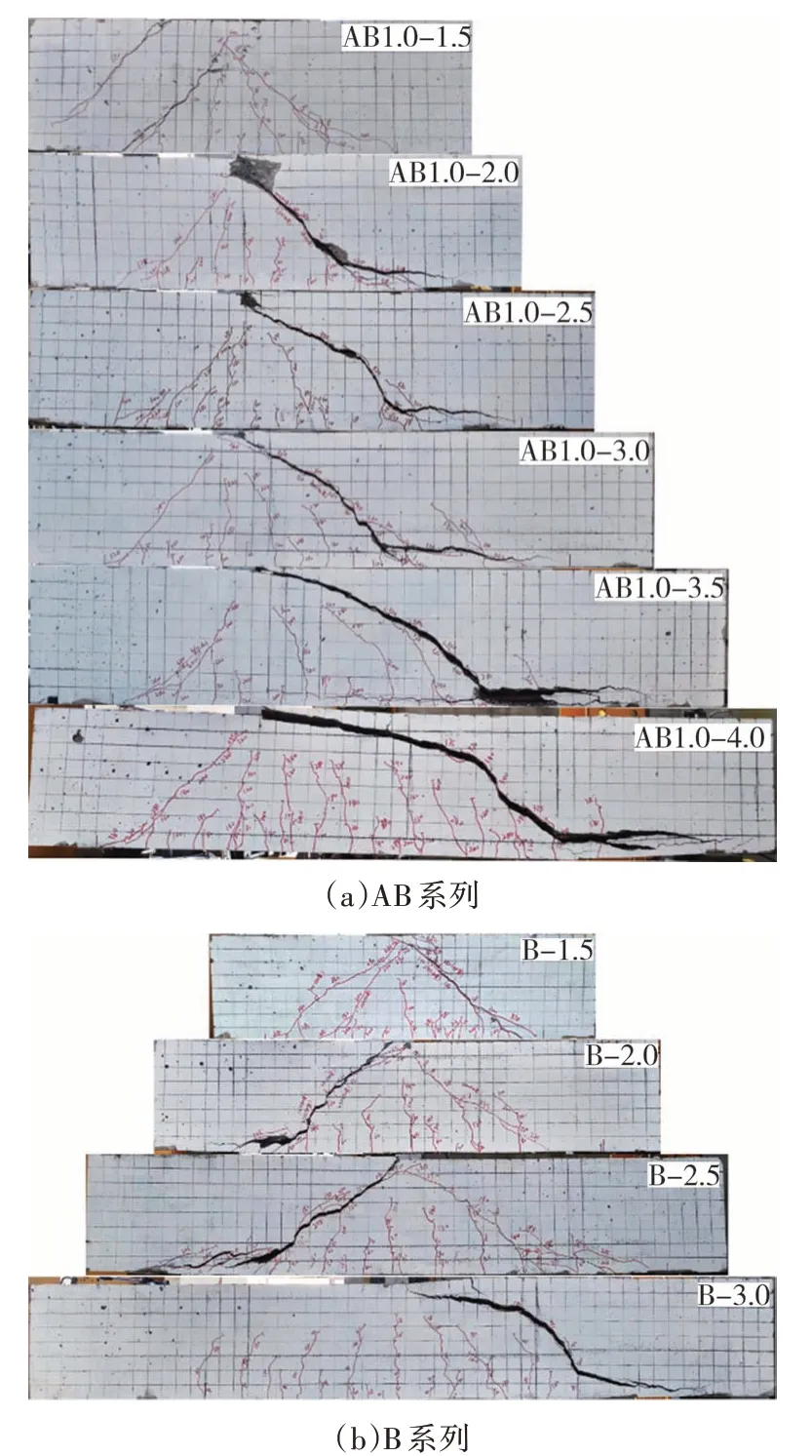
圖4 試件破壞形態(tài)Fig.4 Failure modes of specimens

1）劈裂破壞.試件AB1.0-1.5具有顯著的深梁剪切破壞特征，破壞前大剪跨段已形成貫通的斜裂縫，但由于試件整體延性較高而未立即發(fā)生剪切破壞.隨著荷載的進(jìn)一步增大，梁的小剪跨段上表面距加載點(diǎn)0.5h0處產(chǎn)生劈裂裂縫而導(dǎo)致破壞.

2）剪壓破壞.試件破壞之前，試件AB1.0-2.0、AB1.0-2.5、AB1.0-3.0 和B-1.5、B-2.0、B-2.5 均形成了明顯的臨界斜裂縫，但未立即發(fā)生剪切破壞.隨著荷載的進(jìn)一步增大，試件最終發(fā)生剪壓破壞.

3）斜拉破壞.接近極限荷載時(shí)，試件AB1.0-3.5、AB1.0-4.0中大剪跨段的斜裂縫以及試件B-3.0中的臨界斜裂縫僅發(fā)展至梁高一半處，隨后試件突然發(fā)生剪切破壞，具有顯著的斜拉破壞特征.其中，試件AB1.0-3.5 和AB1.0-4.0 中大剪跨段靠近支座處的混凝土保護(hù)層出現(xiàn)撕裂破壞現(xiàn)象.

結(jié)合圖4（a）和表1 可知，試件AB1.0-1.5 在小剪跨段發(fā)生劈裂破壞，其余AB 系列試件的剪切破壞均發(fā)生在大剪跨段.當(dāng)AB 系列試件的大剪跨比為2.0～3.0 時(shí)，梁的極限荷載和大剪跨段承受的剪力均隨大剪跨比的增大而降低，故可判定其在大剪跨段形成臨界斜裂縫并最終導(dǎo)致梁發(fā)生剪切破壞.盡管試件AB1.0-3.5 和AB1.0-4.0 最終在大剪跨段發(fā)生斜拉破壞，但兩者的極限承載力分別比試件AB1.0-3.0 高11.5%、11.1%，小剪跨段承擔(dān)的剪力非常接近且均高于試件AB1.0-3.0.由此可見，試件AB1.0-3.5 和AB1.0-4.0的極限承載力主要由小剪跨段控制.

2.2 裂縫發(fā)展

所有試件達(dá)到極限荷載的30%左右時(shí)，加載點(diǎn)正下方出現(xiàn)彎曲裂縫并逐漸向上延伸；當(dāng)達(dá)到極限荷載的50%左右時(shí)，基本上不再產(chǎn)生新的豎向彎曲裂縫.隨著荷載繼續(xù)增大，最外側(cè)的豎向彎曲裂縫逐漸傾斜并向荷載作用點(diǎn)延伸.其中，AB 系列試件先在小剪跨段產(chǎn)生斜裂縫.B 系列試件發(fā)生破壞之前，兩剪跨段的裂縫基本上呈對(duì)稱分布狀態(tài)，發(fā)生剪切破壞的區(qū)段具有隨機(jī)性.其中，試件B-3.0 的裂縫發(fā)展過程如圖5（a）所示.

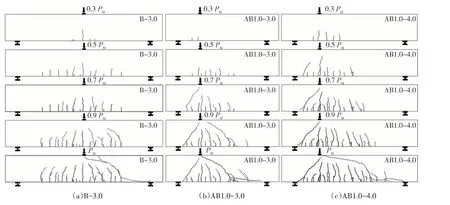
圖5 裂縫發(fā)展過程Fig.5 Crack development processes

試件AB1.0-3.0 的裂縫發(fā)展過程，如圖5（b）所示.當(dāng)加載至極限荷載的30%時(shí)，大剪跨段未出現(xiàn)豎向彎曲裂縫.當(dāng)加載至極限荷載的70%時(shí)，小剪跨段先形成幾乎貫穿整個(gè)梁高的斜裂縫.當(dāng)加載至極限荷載的90%時(shí)，大剪跨段形成了新的斜裂縫并最終發(fā)展為臨界斜裂縫而導(dǎo)致梁發(fā)生剪切破壞.

對(duì)于試件AB1.0-3.5 和AB1.0-4.0，當(dāng)加載至極限荷載的90%時(shí)，小剪跨段的斜裂縫已完全形成，而大剪跨段仍未出現(xiàn)明顯的斜裂縫.當(dāng)達(dá)到極限荷載時(shí)，大剪跨段突然出現(xiàn)斜裂縫而導(dǎo)致梁發(fā)生斜拉破壞.其中，試件AB1.0-4.0 的裂縫發(fā)展過程如圖5（c）所示.

2.3 荷載-跨中位移曲線

試件的荷載-跨中位移曲線，如圖6 所示.結(jié)合表1 和圖6 可知，對(duì)于AB 系列試件，當(dāng)大剪跨比由1.5 增大至3.0 時(shí)，梁的極限承載力呈降低趨勢(shì)；小剪跨段承擔(dān)的剪力呈現(xiàn)先降低后提高的趨勢(shì)，其拐點(diǎn)出現(xiàn)在大剪跨比為2.5 處.當(dāng)大剪跨比由3.0 增大至3.5 時(shí)，梁的極限承載力及小剪跨段承擔(dān)的剪力提高幅度較大.由于試件AB1.0-3.5 和AB1.0-4.0 的極限承載力主要受小剪跨段控制，故兩者的極限承載力非常接近且均高于試件AB1.0-3.0.AB 系列試件中大剪跨段承擔(dān)的剪力隨大剪跨比的增大而降低，這與B系列試件的變化規(guī)律類似.

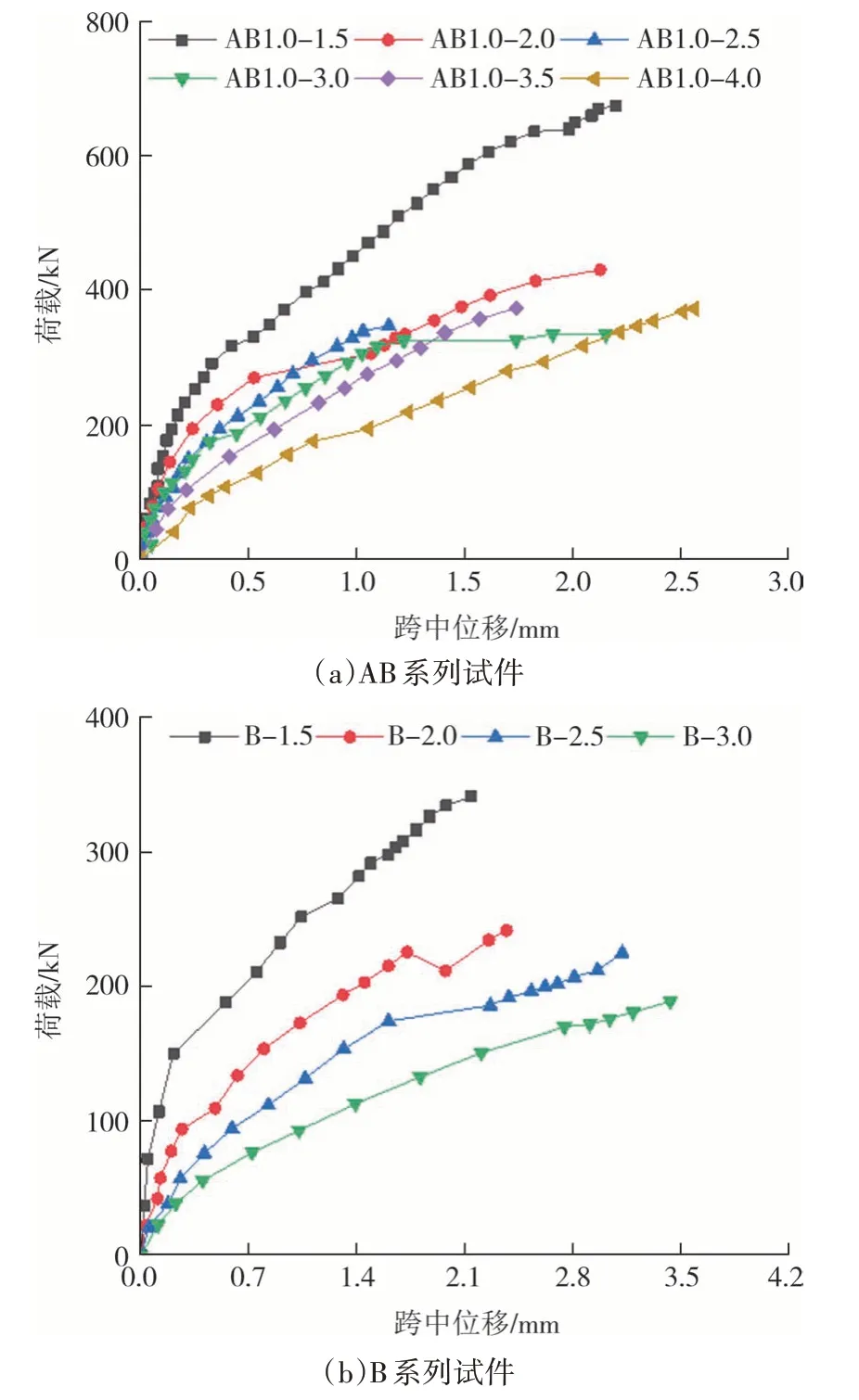
圖6 荷載-跨中位移曲線Fig.6 Load-midspan displacement curves

試件AB1.0-1.5、AB1.0-2.0、AB1.0-2.5和AB1.0-3.0中大剪跨比分別與試件B-1.5、B-2.0、B-2.5和B-3.0 的剪跨比相同.其中，試件AB1.0-1.5 和AB1.0-2.0 中大剪跨段承擔(dān)的剪力分別比B-1.5 和B-2.0 提高了58.0%、14.2%，而試件AB1.0-2.5 和AB1.0-3.0大剪跨段承擔(dān)的剪力分別比B-2.5 和B-3.0 降低了12.0%、11.5%.上述現(xiàn)象，在一定程度上反映出非對(duì)稱荷載作用下鋼筋混凝土無腹筋梁受剪機(jī)理的復(fù)雜性，小剪跨段對(duì)大剪跨段的受剪承載力產(chǎn)生了顯著影響.

2.4 縱筋應(yīng)變分析

所有試件發(fā)生剪切破壞時(shí)，加載點(diǎn)正下方的縱向受拉鋼筋均未屈服.其中，AB 系列試件中縱向受拉鋼筋部分應(yīng)變隨荷載變化的情況如圖7所示.

圖7 縱筋應(yīng)變-荷載關(guān)系曲線（AB系列）Fig.7 Strain-load relationship curves of longitudinal tensile reinforcement in AB series specimens

從圖7（a）可以看出，AB 系列試件中加載點(diǎn)正下方縱向受拉鋼筋在加載初期的應(yīng)變值較小且基本相同；當(dāng)達(dá)到極限荷載的30%左右時(shí)，由于該部位產(chǎn)生了豎向彎曲裂縫，鋼筋應(yīng)變開始出現(xiàn)不同程度的變化.圖7（b）和圖7（c）表明應(yīng)變片R4 處的應(yīng)變先于R7 出現(xiàn)劇增現(xiàn)象，這與前者所在截面的彎矩大于后者有關(guān).

3 計(jì)算模型誤差分析

假設(shè)非對(duì)稱集中荷載在鋼筋混凝土無腹筋梁中大、小剪跨段產(chǎn)生的剪力分別為VW和VE，而兩剪跨段的實(shí)際受剪承載力分別為RW和RE.其中，VW和VE的大小與剪跨段長度成反比.理論上，當(dāng)滿足式（1）時(shí)，大剪跨段先發(fā)生剪切破壞；當(dāng)滿足式（2）時(shí)，小剪跨段先發(fā)生剪切破壞.

Kani［2］開展了大量鋼筋混凝土無腹筋簡(jiǎn)支梁四點(diǎn)彎曲試驗(yàn)，不同配筋率的4 個(gè)系列試件試驗(yàn)結(jié)果如圖8 所示.其中，所有試件的截面尺寸及有效高度均相同，混凝土圓柱體抗壓強(qiáng)度約為 26.2 MPa.圖8 中抗剪強(qiáng)度νu為梁受剪承載力試驗(yàn)值與截面寬度和有效高度之積的比值；λ為剪跨比；ρ為縱向受拉鋼筋配筋率；混凝土軸心抗拉強(qiáng)度ft，m=0.88 ×并取從圖8 可以看出，相同條件下不同縱筋配筋率的無腹筋梁具有不同的抗剪強(qiáng)度，抗剪強(qiáng)度隨剪跨比的增大而呈非線性變化趨勢(shì)，并均在剪跨比為2.5處出現(xiàn)了明顯拐點(diǎn).

圖8 抗剪強(qiáng)度隨剪跨比的變化Fig.8 Variation of shear strength with shear span-depth ratio

一方面，采用GB 50010—2010公式預(yù)測(cè)文獻(xiàn)［2］中試件的受剪承載力，結(jié)果如圖8 中虛線所示.計(jì)算過程中，剪跨比的取值范圍為1.5～3.0.圖8 表明GB 50010—2010公式預(yù)測(cè)無腹筋梁受剪承載力的精度較差，這與鋼筋混凝土梁斜截面剪切破壞機(jī)理復(fù)雜且規(guī)范公式主要依據(jù)試驗(yàn)結(jié)果取下包絡(luò)線有關(guān).另一方面，采用GB 50010—2010 公式預(yù)測(cè)本文試件兩剪跨段的受剪承載力和，并將其替代式（1）和式（2）中的RW和RE以判斷剪切破壞位置，考慮試件AB1.0-1.5破壞模式的復(fù)雜性而不予討論，結(jié)果見表2.從表2 可知，GB 50010—2010 公式預(yù)測(cè)得到梁發(fā)生剪切破壞的位置均與試驗(yàn)結(jié)果相反.

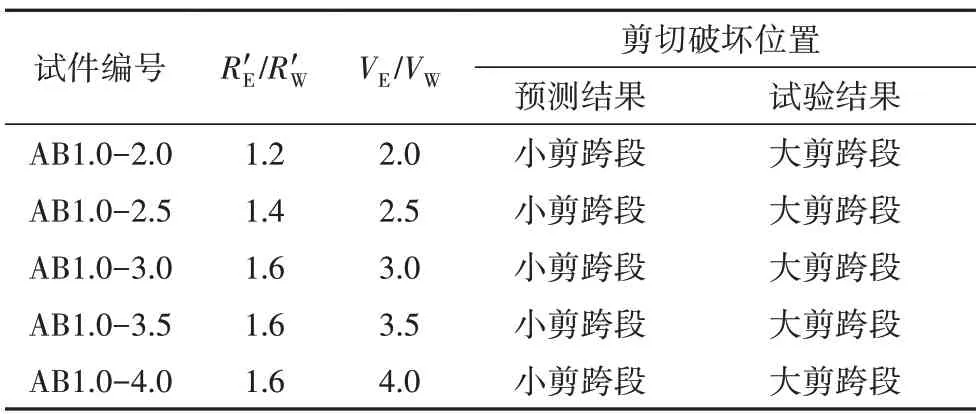
表2 剪切破壞位置Tab.2 The location of the shear failure

MCFT 公式、Choi 公式和Zsutty 統(tǒng)計(jì)公式的計(jì)算表達(dá)式，見表3.采用上述計(jì)算模型分別預(yù)測(cè)AB 系列試件極限承載力及剪切破壞位置，結(jié)果見表4.其中，剪切破壞位置判斷的原則與表2 相同.考慮到同一試件中兩剪跨段的剪跨比不同而不可能同時(shí)發(fā)生剪切破壞，以致不能簡(jiǎn)單地將兩剪跨段受剪承載力的預(yù)測(cè)值直接疊加而得到梁的極限承載力.因此，本文分別利用兩剪跨段的受剪承載力預(yù)測(cè)值推算梁所能承受的荷載Pcal，E、Pcal，W，并取Pcal，E和Pcal，W兩者中的較小值作為極限承載力代表值Pcal.計(jì)算過程中，根據(jù)混凝土立方體抗壓強(qiáng)度實(shí)測(cè)值平均值換算得到圓柱體抗壓強(qiáng)度=34.2 MPa.計(jì)算截面按以下原則選取：MCFT 公式取與支座距離為（a-d）和0.5a中的較大值［20］；Choi公式和Zsutty統(tǒng)計(jì)公式取支座處截面.

表3 計(jì)算模型表達(dá)式Tab.3 Expressions of calculation models

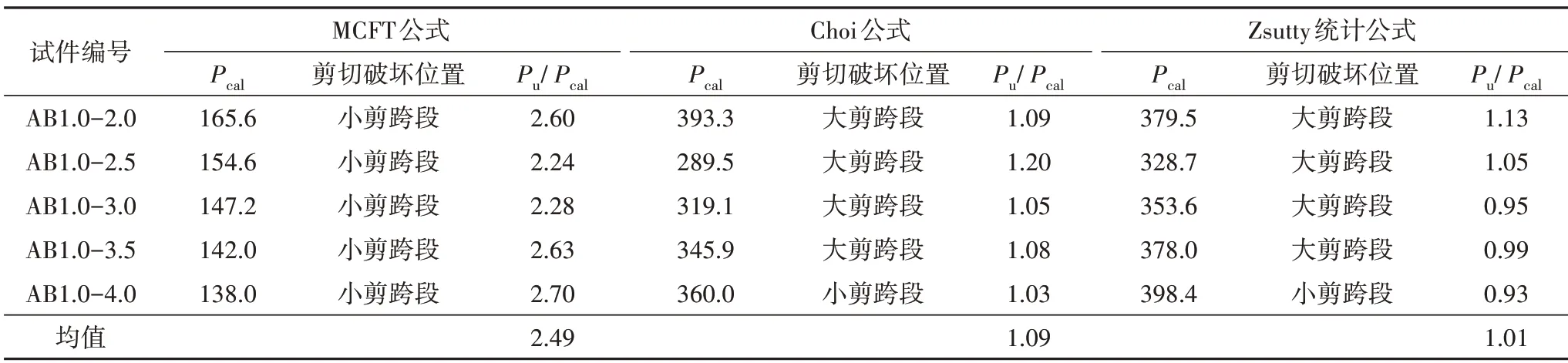
表4 計(jì)算模型預(yù)測(cè)結(jié)果Tab.4 Prediction results of calculation models

從表4 可以看出，極限承載力試驗(yàn)值Pu與MCFT公式預(yù)測(cè)結(jié)果之比的均值為2.49，而且剪切破壞位置的預(yù)測(cè)結(jié)果均與試驗(yàn)結(jié)果相反.Choi 公式和Zsutty統(tǒng)計(jì)公式預(yù)測(cè)得到的Pu/Pcal均值分別為1.09和1.01，且兩者預(yù)測(cè)剪切破壞位置的效果也較理想.相比之下，Zsutty統(tǒng)計(jì)公式的預(yù)測(cè)效果最好.

4 結(jié)論

通過開展6 根非對(duì)稱（小剪跨比恒為1.0）和4 根對(duì)稱集中荷載作用下鋼筋混凝土無腹筋梁受剪性能試驗(yàn)研究及分析，主要得出以下結(jié)論：

1）當(dāng)大剪跨比為2.0～4.0 時(shí)，非對(duì)稱集中荷載作用下鋼筋混凝土無腹筋梁均在大剪跨段發(fā)生剪切破壞，但小剪跨段先于大剪跨段形成明顯的斜裂縫，且梁的極限承載力及小剪跨段承擔(dān)的剪力呈非單調(diào)變化趨勢(shì).

2）非對(duì)稱集中荷載作用下鋼筋混凝土無腹筋梁大剪跨段承擔(dān)的剪力隨著剪跨比的增大而降低，與對(duì)稱集中荷載作用時(shí)受剪承載力的變化規(guī)律相同；小剪跨段對(duì)大剪跨段的受剪承載力產(chǎn)生了顯著影響.當(dāng)大剪跨比由3.0增大至3.5時(shí)，梁的極限承載力出現(xiàn)由大剪跨段控制轉(zhuǎn)變?yōu)樾〖艨缍慰刂频默F(xiàn)象.

3）對(duì)于非對(duì)稱集中荷載作用下鋼筋混凝土無腹筋梁，采用《混凝土結(jié)構(gòu)設(shè)計(jì)規(guī)范》（GB50010—2010）公式預(yù)測(cè)發(fā)生剪切破壞位置的結(jié)果與試驗(yàn)現(xiàn)象相反，修正壓力場(chǎng)理論模型預(yù)測(cè)極限承載力過于保守且不能準(zhǔn)確判定剪切破壞的位置，而Zsutty統(tǒng)計(jì)公式的預(yù)測(cè)效果最好.