基于科技項目評審專家異質性的共識測度方法

李 山，王 俊，趙旭東

（1.華東交通大學經濟管理學院，江西南昌 330013；2.江西新型智庫數據中心，江西南昌 330013）

0 引言

現行同行評議制度下，非共識項目由于其風險性與同行評議制度的不相適應，導致此類項目大量落選［1-2］。非共識項目所蘊含的重大創新是現代科學發展所必需的元素，近現代科學許多重大發現與突破都發源于蘊藏著潛在機遇的非共識項目［3］。因此非共識項目的再挖掘就顯得尤為重要［4］。對于非共識項目的再挖掘，首先就是推薦合適的專家組［5］，若僅依據現有專家推薦要素即專家研究方向、學術關系等遴選專家［6-7］，專家的評審認知依舊可能會導致非共識現象大量存在［8］。共識度反映的是專家組評審總體認知，共識度越高，越利于非共識項目的再挖掘［9］，因此，若要為非共識項目的再挖掘推薦合適的專家組，有必要引入評審專家群體共識度測算。國內外共識度的相關研究傾向于偏好相似程度的度量和集結［10］，集中于OWA 算子、模糊語義量化等方法［11］。在項目評審領域，暫未出現專家評審共識度計算的相關文獻，因此本文利用科技項目同行評議數據，結合歷史評審數據與專家知識計算共識度，充分考慮專家歷史信息與當下信息，在保證相對客觀的同時，也能反映專家的主觀偏好信息。本文提出的共識度測算方法具體過程是以2020 年某科研類科技項目評審數據為研究對象，評審專家有著豐富的學術背景，存在大量公開發表的論文等數據可以作為專家知識度量的依據。因此，首先通過這些學術型評審專家歷史評審數據［12］構建的專家先驗權重，結合反映專家異質性的主題覆蓋度和權威度［13］確定的專家后驗權重，得到最終的專家權重，再利用互反矩陣共識決策算法［14］11計算專家評審結果的共識方案排序，并利用排名偏差重疊計算每位專家的評審共識度。

1 文獻綜述

大群體決策共識過程是指決策群體通過討論或其他方式協調不同意見與看法，達成某種意義上的一致，最終做出決策［15］，此過程主要包含群體共識度的測度以及非共識的修正兩個步驟［16-17］。科技項目評審亦屬群體決策，對于難以做出決策的非共識項目，則需要為其推薦合適的專家組對其進行再挖掘［18-19］。現有專家遴選標準主要包括專家權威度、專家知識結構、主題匹配度、專家學術關系網等［20］，若依舊按照現有標準遴選專家，評審專家的主觀認知和偏好依舊會導致非共識現象的產生［21］。共識度反映的是專家組評審偏好的一致性，共識度越高，越利于挖掘出有價值的非共識項目［9］，因此針對非共識項目的評審專家推薦，需要引入反映專家評審偏好的共識度。但由于群體內的異質性難以量化，共識度的難以測度直接對決策環境的共識進程產生影響，因此，共識度的測度一直是研究熱點［22］。現有研究主要集中于偏好相似程度的度量和集結中［10］。在偏好相似程度的度量方面，Liu 等［23］依據曼哈頓距離計算偏好相似度；Wu 等［24］提出度量偏好相似程度的重要依據之一是個體評價的傳遞性特征；王運等［25］融合用戶與物品之間關系提出了偏好相似度的概率矩陣分解推薦算法；Wang 等［26］和Zhang等［27］都利用了規劃模型測度并改進個體評價中的偏好相似程度。在偏好關系的集結方面，OWA 算子是最經典的集結模型［28］；Liu 等［11］依據決策者自信程度集結偏好關系；羅世華等［29］提出一種改進的Choquet Bonferroni 算子，將偏好關系轉化為決策者權重后再集結；Del 等［30］通過測算不同集結方式對群體共識度的影響，提出了基于有序集結算子的集結模型。根據上述研究，發現群體共識度測算存在以下不足：一方面，現有文獻對科技項目評審共識度的關注較少；另一方面，專家的異質性在測算中并未得以區分，如專家研究方向、權威度的差異極易導致共識度的計算產生偏差，且未考慮專家歷史評審偏好。基于以上考慮，本文提出了一種結合歷史信息與當下信息的共識度測算方法，選擇某次科技項目專家評審數據為研究對象，結合此次評審專家的歷史評審數據測度歷史評審偏好，并結合專家研究背景知識計算此次評審活動的群體共識度。

在方法的選擇上，群體共識是現代決策科學的重要組成部分，是目前決策領域的研究熱點之一，國內外在共識模型、算法及其應用等方面具有深度研究［31］。吳志彬［14］11在《群體共識決策理論與方法》中闡述的基于互反矩陣的群體共識決策方法，不僅考慮了個體理性和群體理性，而且分別給出了個體一致性改進和群體共識達成的算法，具有良好的可調節性。因此本文選擇互反矩陣共識決策用以計算依據專家評審數據達成的共識決策方案，但此方法在專家權重確定時主觀賦予每位專家相同權重，專家的異質性并未得以體現。權重作為專家異質性的一種重要表達方式，一直都是群體決策領域的重點研究問題［32］，學者從很多方面對該問題展開了研究。易平濤等［12］根據數據聚類思想及信息集結方法、時間權向量的求解思路，給出了一種兼顧專家先驗權重和后驗權重的權重確定方法；趙千等［13］提出融合主題覆蓋度和專家權威度的專家推薦框架，綜合考慮覆蓋度和權威度兩種因素作為專家權重。本文為計算專家的異質性，首先借助易平濤等［12］人的研究提出的先驗權重確定方法，以專家歷史評審數據確定專家歷史評審偏好作為先驗權重；其次參考趙千等［13］人的研究提出的專家權重確定方法，結合專家研究方向與項目內容的相似度、權威度作為后驗權重；最后結合先驗權重與后驗權重得到最終專家權重。此權重確定方法同時兼顧專家歷史信息和當下信息，并考慮了專家研究方向、權威度等極易導致共識度產生偏差的指標。由于后驗權重的計算依賴于專家公開發文數據作為基礎，因此本次研究對象針對的是科研類科技項目評審專家，這些專家均有豐富的學術背景，有著大量公開發表的論文，可以用于測度專家知識。確定專家權重后，以互反矩陣共識決策計算本次評審活動的共識決策方案，再利用Chen 等［33］提出的排名偏差重疊計算每位專家與共識決策方案的相似程度得到群體共識度。

2 問題描述與條件假設

本文要解決的問題是：一是決策者異質性權重的獲取。在過往共識度的計算中，決策者異質性一直是難點之一，本文利用決策者背景數據，通過Word2Vec 詞向量模型、Critic 法等方法測度異質性權重。二是共識度的獲取。借助客觀數據，通過互反矩陣共識決策模型獲取共識決策方案，并對比各決策者方案，通過排名偏差重疊計算得到共識度。為了更準確地說明問題，現給出2 個假設：

（1）決策者均為本次評價活動專業相關領域的專家；

（2）各位專家的判斷具有一定的穩定性。

3 基礎知識

3.1 互反矩陣

3.2 個體一致性度量

根據吳志彬等［14］12關于個體一致性的度量標準，給出以下的定義。

則稱A為具有滿意一致性的互反矩陣。

3.3 共識程度度量

定義5：令A1,A2,,Am為m個互反矩陣。假設是由幾何平均算子集結得到的群體互反矩陣。的群體共識一致性指標定義為

4 方法與基本原理

4.1 決策者權重的確定

m個決策者針對n個項目做決策，在決策過程中由于決策者之間研究方向、判斷水平等知識存在差異，每位決策者以不同的方式解釋評價指標，導致決策者最終決策未能達成共識。

4.1.1 決策者先驗權重

通過歷史評審數據來反映決策者的歷史評審水平，并與最終評審結果對比［12］。具體過程如下：

（1）收集每位決策者歷史評審數據，將每位決策者評審數據處理為表1 形式。

表1 決策者歷史評審信息

（2）決策者歷史序值相關系數的計算。本文采用斯皮爾曼等級相關系數對決策者在不同時期內的評審結果進行序值的相關系數計算，其計算公式為：

式（6）中：d表示序值之間的差距，j表示等級個數，序值一致性越高r越大。

（3）運用指數平滑推測本次評審中決策者的序值相關系數。一次指數平滑的公式為：

4.1.2 決策者后驗權重

在評審過程中，由于決策者研究方向的影響，決策者對與自己研究方向相近的評審項目會有更清晰的判斷，因此以主題覆蓋度來反映該影響因素。同時，決策者權威度會導致決策的可信度產生偏差，因此選擇將主題覆蓋度與決策者權威度同時納入專家權重的計算，并稱之為后驗權重。

（1）主題覆蓋度。

利用決策者發文摘要與項目研究內容，通過Word2vec 詞向量模型輸出摘要-研究內容詞對，計算余弦相似度，以此反映決策者研究方向與評審項目研究內容的相關程度，即主題覆蓋度。具體步驟如下：

①將決策者發文摘要與評審項目研究內容去除停用詞，切分成詞的形式并導入語料庫，處理成Word2vec 模型的訓練格式。

②建立所有決策者的發文摘要與所有評審項目研究內容的Word2vec 詞向量模型。

③通過余弦相似度對訓練得到的摘要—研究內容詞向量計算決策者發文摘要與評審項目研究內容的相似程度。余弦相似度的計算公式為：

④主題覆蓋度權重計算公式為：

（2）決策者權威度。

決策者權威度的計算需要利用決策者論文發表量、h 指數、被引量等指標信息，通過critic 權重法對決策者權重進行計算。具體步驟如下：

①獲取決策者論文發表量、h 指數、被引量等指標信息，并處理為critic 權重法所需的數據類型。

②對各指標歸一化處理。正向指標的做法為：

負向指標的做法為：

③變異性的處理。在critic 權重法中利用標準差表示變異性，變異性較大的決策者信息，反映出更多信息，應賦予更高的權重。變異性的計算公式為：

④沖突性。決策者之間的相關系數越大，沖突性就越小，權重也越小。critic 權重法中使用相關系數的形式反映相關性，計算公式為：

⑤信息量越大的決策者應被賦予更高的權重，信息量的計算公式為：

⑥權重的確定。

（3）后驗權重的確定

第q位決策者后驗權重為：

4.1.3 決策者最終權重

在本次評審中，決策者最終權重為

4.2 互反矩陣共識決策

互反矩陣共識決策是在同時考慮個體理性與群體理性的情況下，給出個體一致性改進和群體共識達成的算法，一共分為個體一致性控制階段、共識達成階段、方案排序階段3 個階段［14］14。

4.2.1 個體一致性控制算法

算法1：互反矩陣的個體一致性改進。

個體一致性控制階段的具體過程。

（1）根據定義1，從各決策者對項目的決策數據中，提取出m位決策者初始偏好信息A1,A2,,Am；

4.2.2 共識達成算法

算法2：基于互反矩陣的共識達成過程。

個體一致性控制階段實現后，共識達成階段的過程如下：

4.2.3 方案排序

4.3 共識程度的獲取

獲取排序列表后，借助排名偏差重疊（rank biased overlap，RBO）計算每個決策個體的排序列表與群體的共識程度［33］，計算步驟如下：

假設S為決策個體的排序列表，T為群體互反矩陣對應的排序列表。為列表S的第i個元素，表示列表中從位置c到位置d所有元素組成的集合。在深度為d時，列表S和T的交集為：

交集的元素個數相對于深度d的比值稱為列表S和T的一致度，再賦予每個深度的一致度權重,得到相似度：

因此，設定參數p，排名偏差重疊（RBO）距離度量方法可以簡化為

RBO 指標范圍在［0,1］之間，值越接近1 表示列表之間共識程度越高。

5 應用算例

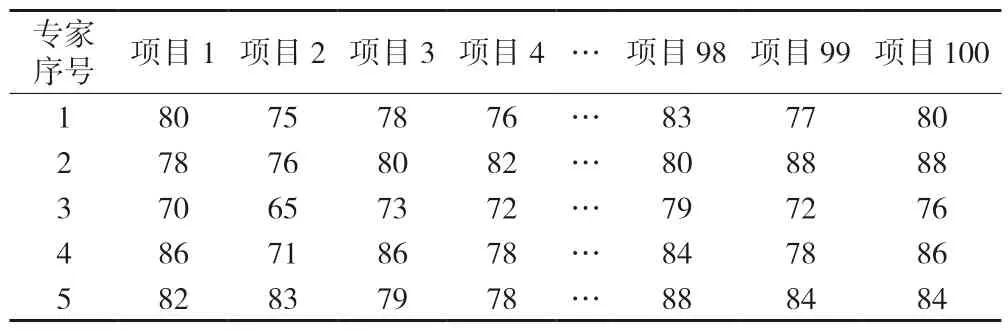
表2 專家評分 單位：分

5.1 專家權重的確定

5.1.1 專家先驗權重的確定

5 位學術型專家的先驗權重計算結果為

表3 專家評審數據 單位：分

表3 專家評審數據 單位：分

表4 專家群最終評審數據 單位：分

表5 專家序值信息

表5 專家序值信息

表6 專家群序值信息

表7 專家序值相關系數表

表7 專家序值相關系數表

5.1.2 專家后驗權重的確定

（1）主題覆蓋度

主題覆蓋度反映的是每位學術型專家所有發文摘要與評審項目研究內容的余弦相似度，根據4.1.2主題覆蓋度的計算過程所述得到結果為

計算過程如下：

①收集每位專家所有發文摘要與評審項目的研究主題，利用Python 的jieba 庫將其分詞后，再加載停用詞，去除停用詞后導入語料庫中。

②利用每位專家發文摘要的語料庫，結合評審項目研究主題的語料庫訓練Word2vec 模型，訓練出5 位專家的Word2vec 詞向量模型。

③定義余弦相似度求取函數，并利用5 位專家的Word2vec 詞向量模型求取每位專家的余弦相似度，結果為

④主題覆蓋度權重的確定。5 位學術型專家主題覆蓋度權重為

（2）專家權威度

專家判斷的差異對于項目評審的影響是毋庸置疑的，本文利用學術型專家權威度反映專家判斷水平，所使用的指標包括專家學位、評審年份、參與評審的課題、論文發表量、著作數量、h 指數、被引量等指標數據，通過critic 權重法對學術型專家賦權，根據4.1.2 決策者權威度的計算過程所述得到結果為

計算步驟如下：

①獲取5 位學術型專家學位、評審年份、參與評審的課題、論文發表量、著作數量、h 指數、被引量等指標信息，并將其處理為critic 權重法所需的數據類型。

②由于指標特征值都有含義，因此不需要對負向指標、正向指標標準化，每位專家的變異性為

③計算沖突性。沖突性相關系數為

④計算信息載量。5 位專家的信息載量是

⑤根據信息載量獲得5 位專家權威度權重分別為

（3）后驗權重的確定

根據公式（18），由于主題覆蓋度與專家權威度對項目評審的影響都不可忽視，因此本次取0.5，最后求得專家后驗權重為

5.1.3 專家最終權重

5.2 互反矩陣共識決策

確定專家權重后，為方便進行基于互反矩陣的共識決策，需要將每位專家當期100 個評審項目的評分數據轉化為互反矩陣。本文將每位專家評分的極差九等分，得到定義1 中的互反矩陣，根據專家一的評分數據轉化為的互反矩陣如表8 所示。得到5 位專家的互反矩陣后，即可按照基于互反矩陣的決策支持模型來獲取專家決策共識情況。

表8 專家一互反矩陣

表8 專家一互反矩陣

5.2.1 個體一致性控制階段

計算5 位專家的初始一致性指標，由于數據量較大，計算過程均通過Python 實現，此處僅列出計算結果。步驟如下：

（1）群體互反矩陣Ac的構造。根據5 位專家的權重

結合定義2 構造的群體互反矩陣如表9 所示。

表9 群體互反矩陣

表9 群體互反矩陣

（2）一致性指標矩陣的構造。根據定義3，對5 位專家的互反矩陣A1,A2,A3,A4,A5以及Ac分別構造出含一致性指標的矩陣，根據專家一互反矩陣構造的如表10 所示。

表10 矩陣

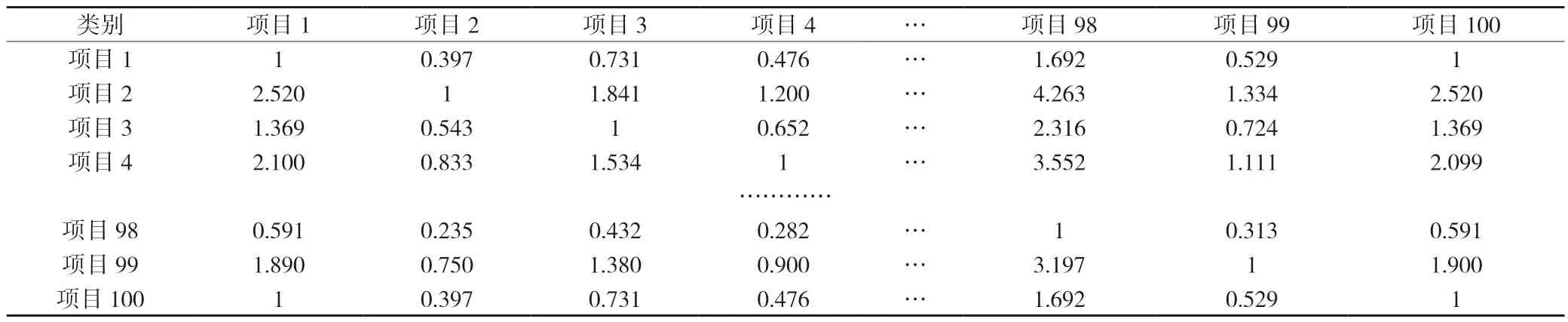
表10 矩陣

5.2.2 共識達成階段

每位專家的共識一致性指標值的計算及修正步驟如下：

（1）群體共識指標GCIH(A)的計算。根據定義5，5 位專家的互反矩陣A1,A2,A3,A4,A5結合群體互反矩陣得到群體共識指標為

表11 共識指標修正過程

表12 處理后的群體互反矩陣

表12 處理后的群體互反矩陣

經過17 次迭代之后，修正后的群體一致性指標值為

5.2.3 方案排序階段

圖1 的排序

圖2 專家的排序

圖3 專家的排序

圖4 專家的排序

圖5 專家A4的排序

圖6 專家的排序

5.3 共識度計算

得到排序列表后，將每位專家的排序列表與共識達成后的排序列表進行對比，設置p值為0.9，按照RBO 算法計算得到共識度為

5.4 對比分析

為展示本文方法的可行性與合理性，本文選擇基于決策者一致性水平、群體共識度水平兩方面數據與傳統共識決策模型進行效果對比，具體過程是用傳統共識決策模型計算本文案例的共識決策方案。

圖7 決策者性水平對比

圖8 群體共識度水平對比

綜上所述，本文對于科研類科技項目評審的學術型專家共識測度方法充分考慮了歷史信息和當下信息，充分挖掘了專家異質性的測度，計算過程中加入專家歷史評審偏好、主題覆蓋度、專家權威度等易對共識度計算產生影響的異質性指標，均以客觀數據信息為依據，減少了主觀信息的影響，使得整體結果在個體一致性水平和群體共識度水平上均有一定程度的提升，相比傳統的共識決策模型有更好的適用性和靈活性。

6 結論

迄今，已有研究證明可對偏好相似程度進行度量和集結，但對于專家之間的異質性考慮較少，且鮮見利用評審數據測度專家共識的文獻。本文提出的專家共識測度方法特點是利用科技項目評審數據、專家知識，考慮專家歷史評審偏好的差異，結合主題覆蓋度與專家權威度體現專家之間的異質性，進而通過互反矩陣共識決策模型計算專家共識度。從問題解決效果來看，本文設計的研究思路及決策步驟，充分考慮了影響決策進程達成共識的因素——專家異質性，解決了科技評審專家的共識測度問題，為非共識項目的再挖掘做好了鋪墊。由于本次研究對象主要是科研類科技項目的評審，評審專家學術背景豐富，均有發文作為數據分析的基礎，忽略了缺少研究論文數據支持的技術型專家的共識測度問題，從而使得本研究存在一定的局限性。但這也是下一步研究工作的重點，即將非科研類科技項目評審專家間的共識度納入評審專家推薦模型中，為非共識項目推薦合適的專家組進行再挖掘，以此提升科技項目評審的準確性與整體質量，推動科技項目研究水平的穩步發展。