分數階光敏神經元的動力學特性分析及其同步研究
楊寧寧 孟詩悅* 吳朝俊
①(西安理工大學電氣工程學院 西安 710048)
②(西安工程大學電子信息學院 西安 710048)
1 引言
神經系統是一個龐大而復雜的網絡,是由眾多神經元通過突觸連接形成的信息網絡[1]。神經元作為神經系統的基本結構和功能單位,能夠感知和傳遞刺激,具有連接和整合輸入信息和傳遞信息的功能[2]。當神經元受到刺激時,細胞膜內外的離子濃度會發生突變,從而觸發動作電位[3]。這種電生理信號沿軸突傳輸到突觸前端,進一步被相鄰神經元的突觸后端捕獲和感知,實現神經元之間信號的傳輸和編碼。單個神經元在受到相鄰神經元或外部刺激后,可誘發多種放電模式,如靜息態、周期放電態、混沌放電態等復雜的放電模式。在實際環境中,神經元并不是獨立存在的,而是彼此通過突觸相互耦合、相互影響的。因此搭建神經元電路為研究其復雜的非線性動力學行為和信息傳輸提供了有效的途徑[4-6]。常見的神經元模型有Hodgkin-Huxley模型[7]、FHN模型[8]、Hindmarsh-Rose模型[9]、Izhikevich[10]模型等。
在實際的生理環境中,神經元會受到如光照、溫度、外磁場等外部刺激的影響,此時其輸出電壓可以反映神經元電路的興奮性。馬軍[11]在單個神經電路中嵌入不同的物理器件設計了光敏神經元、熱敏神經元等多種功能神經元。Liu等人[12]用光電管來激活FHN神經元模型,詳細地分析了系統參數對神經元放電模式的影響。現有的基于理想元件的神經元電路研究主要集中在整數階,而研究表明分數階神經元模型更精確,可以提高信息處理的效率。Yao等人[13]分析了分數階FHN神經元的動力學特性,并證明了分數階神經元更適合與模擬神經行為。Yang等人[14]研究了憶阻突觸耦合分數階神經元的同步特性。研究結果表明隨著分數階階次的變化,神經元在周期態和混沌態之間過渡。Abdelaty等人[15]研究表明分數階模型由于額外的自由度,可以豐富模型的靈活性和動態特性。
本文的其余部分組織如下:在第2節中,提出了分數階光敏神經元模型;在第3節中,通過分岔圖、相軌跡圖和時間序列圖等方法分析了分數階光敏神經元的動力學行為;在第4節中,采用dSPACE驗證了仿真結果。最后,對全文進行了總結并說明了本文所提出的模型潛在的應用前景。
2 分數階光敏神經元數學模型
光線進入眼睛,在視網膜上感光并觸發神經電活動響應,從物理過程來看視網膜實現了光電轉換,把電磁波能量轉化為生物電信號,并以動作電位的方式進一步刺激腦視覺功能區來產生響應。光敏神經元模型可以近似模擬這一物理過程,而分數階光敏神經元比整數階模型更精確,動力學行為更豐富,此節介紹分數階光敏神經元模型。
2.1 分數階光敏神經元
本文在文獻[16]整數階光敏神經元的基礎上,用分數階電容和電感替代整數階神經元電路中的理想元件,得到了分數階光敏神經元電路模型,如圖1所示。其中 NR 是非線性電阻,C表示分數階電容,L為分數階電感,R是與感應線圈串聯的電阻,iS代表外部刺激電流,E為施加的恒定電壓源,VS為余弦電壓源,RS為支路的電阻。
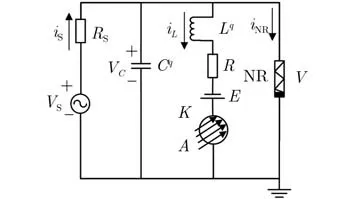
圖1 分數階光敏神經元電路示意圖
根據基爾霍夫定律、伏安關系及分數階電容、電感模型[17,18]得到圖1的電路方程為
非線性電阻 NR的電壓和電流之間的關系表達式為[16]
其中,ρ,V0是電阻的歸一化參數;V是非線性電阻的電壓。
對電路方程式(1)采用以下的無量綱變換
從而得到分數階光敏神經元的動力學方程[19]
其中,x表示膜電位,y表示恢復變量對應的慢電流, 0<q ≤1 是分數階的階數,a,b,c,ξ是系統參數。外部激勵源和光電管輸出為uS=B1cosωτ,且ug=B2cosωτ。其中B1、B2和ω分別表示激勵和光電管的幅值和頻率。也就是說,光電管可以用作電壓源,產生時變刺激,激活神經回路。
2.2 穩定性分析
從分數階系統(4)中移除外部電壓源和光電管輸出,對此神經元進行穩定性分析
假設平衡點為 (x0,y0),此點的雅可比矩陣為
相應的特征方程為
相應的特征值為
如果其中一個特征值滿足
平衡點是不穩定的。顯然,它是由參數a,b,c和參數ξ決定的。
3 數值仿真及動力學分析
在本節中,通過數值仿真分析分數階光敏神經元模型的動力學特性。系統的歸一化參數選取為a=0.7,b=0.8,c=0.1,ξ=0.175,變量初始值為(x0,y0)=(0.2,0.1)。
3.1 分數階階次q =0.99
取參數B1=0.8,ω=0.4,B2=0.2,繪制系統的動力學隨參數B1和ω變化的分岔圖,如圖2所示。可以看出,改變外界驅動參數B1和ω,可以使系統在周期放電和混沌放電之間過渡。
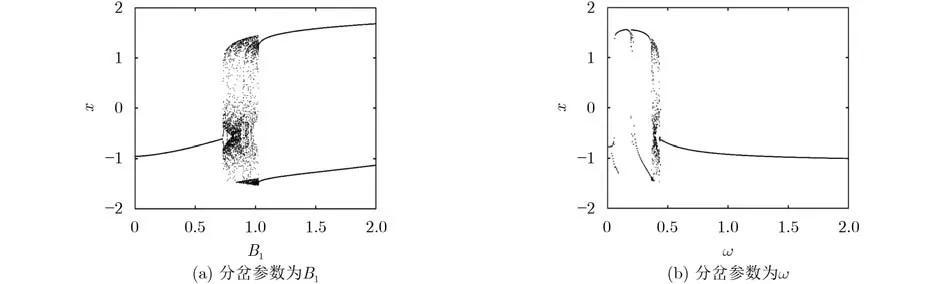
圖2 q=0.99時不同分岔參數下的分岔圖
當固定其他參數不變時,隨著參數B1的增大,系統由單周期放電過渡到混沌放電狀態,而后轉變為雙周期放電狀態(圖3)。若只改變參數ω,系統經過單周期放電、尖峰放電過渡到混沌放電,而后轉為雙周期放電狀態(圖4)。結果表明,在不同的參數選擇下,系統膜電位可以呈現出不同的放電模式,即周期放電態、尖峰放電態及混沌放電態。
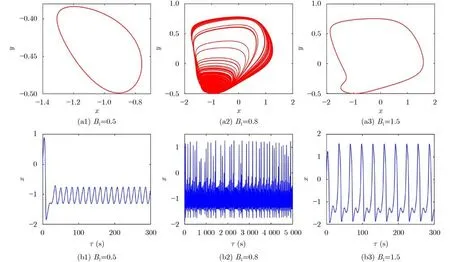
圖3 q=0.99時參數B1取不同值時的相圖及時間序列圖
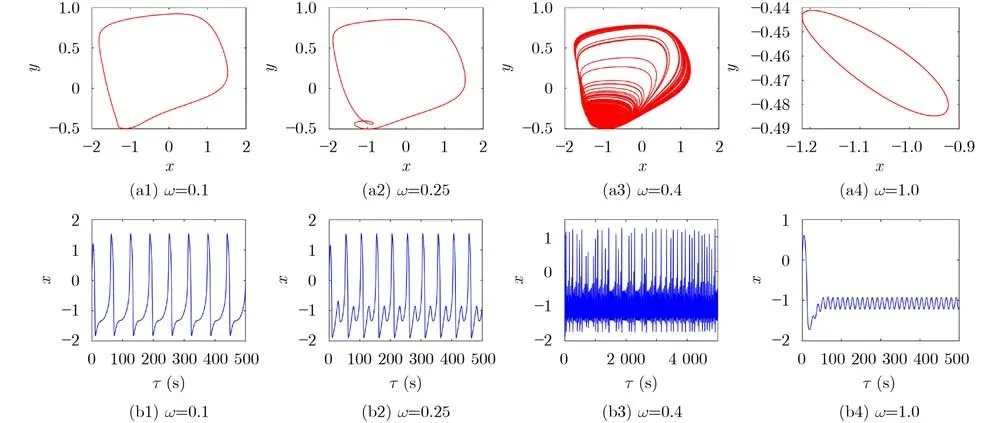
圖4 q=0.99時參數ω取不同值時的相圖及時間序列圖
3.2 分數階階次q =0.9
取參數B1=0.8,ω=0.4,B2=0.2,隨參數B1和ω變化的分岔圖如圖5所示。可以看出,隨著分數階階次的降低,系統的混沌區域減少且時間滯后,神經系統對外界信號的適應能力增強。
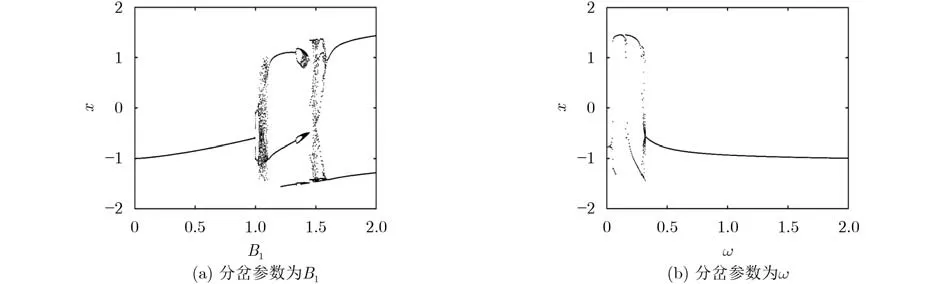
圖5 q=0.9時不同分岔參數下的分岔圖
當固定其他參數不變時,隨著參數B1的增大,系統在周期放電狀態和混沌放電狀態之間轉換(圖6)。若只改變參數ω,系統經過周期放電過渡到混沌放電,而后轉回單周期放電狀態(圖7)。結果表明,在不同的參數選擇下,系統膜電位可以呈現出不同的放電模式,即周期放電態、尖峰放電態及混沌放電態。
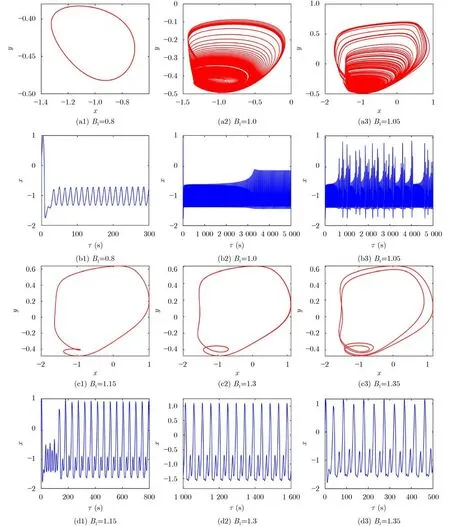
圖6 q=0.9時參數B1取不同值時的相圖及時間序列圖
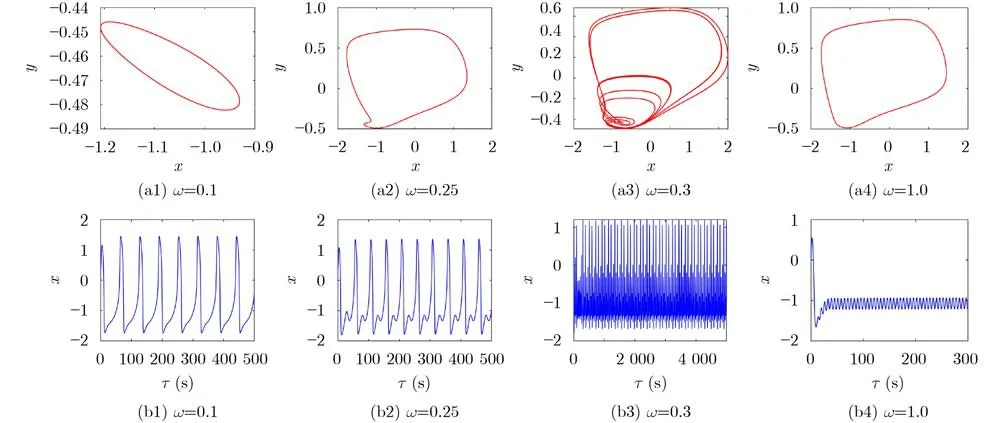
圖7 q=0.9時參數ω取不同值時的相圖及時間序列圖
3.3 隨分數階階次 q 變化
考慮到分數階階次q的變化對分數階光敏神經元電路動力學特性的影響。取B1=0.8,ω=0.4,B2=0.2,q ∈[0.9,1] 。系統隨階次q變化的分岔圖如圖8所示。由圖可以看出,系統隨階次變化的分岔圖可以分為兩種狀態:周期狀態和混沌狀態。當q ∈[0.9,0.962] , [0.967,0.97] , [0.973,0.974]時,系統處于周期態,當q ∈[0.962,0.967] , [0.97,0.973],[0.974,1]時,系統會表現出復雜的混沌狀態。
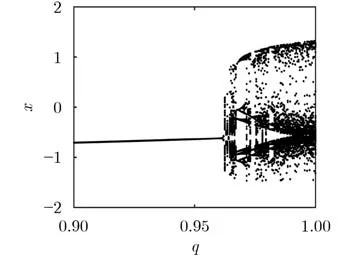
圖8 系統隨階次q變化的分岔圖
3.4 基于電突觸耦合策略的分數階光敏神經元的同步控制
神經元同步在大腦信息交流和處理的過程中發揮了重要的作用。本文采用電突觸耦合方式實現了兩個分數階光敏神經元的同步。如果忽略耦合的時間延遲,則兩個光敏神經元組成的系統為其中:a,b,c,ξ是參數,r是耦合強度,0<q ≤1是分數階的階數。
設e1=x1-x2,e2=y1-y2,若t →+∞時,有e=|e1|+|e2|→0,則兩個耦合神經元達到完全同步。取定系統的歸一化參數B1=0.8,ω=0.4,B2=0.2,r=50, 系統初始值為 (x1,y1)=(0.2,0.1),(x2,y2)=(0.02,0.01) ,分數階階次q=0.99和0.9,光敏神經元不同階次對初值的同步如圖9所示。
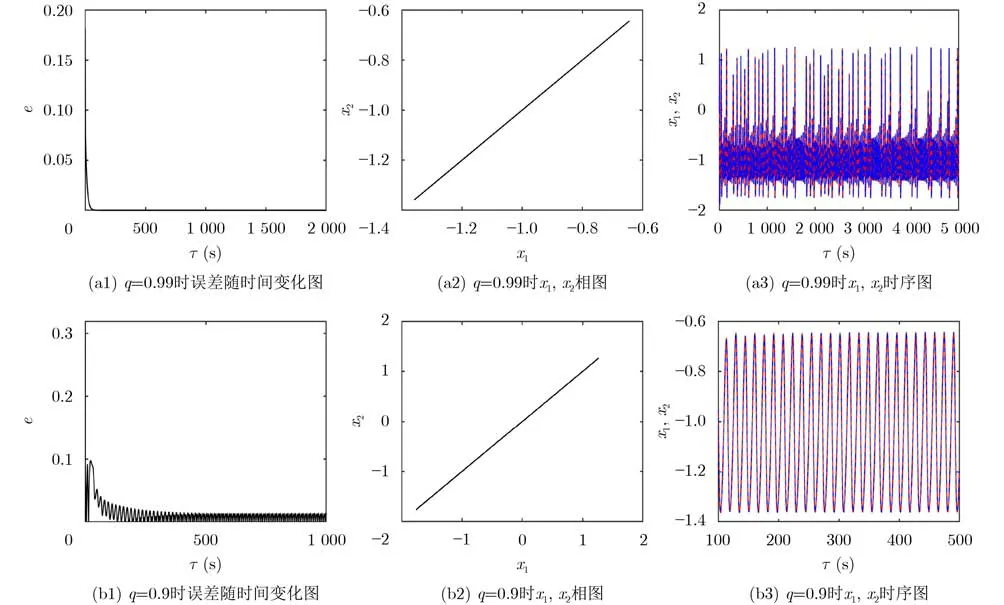
圖9 光敏神經元不同階次對初值的同步
由圖9可知,在相同的耦合系數下,當q=0.99時,兩個分數階光敏神經元之間可以達到完全同步;當q=0.9時,兩個光敏神經元之間相位同步,尖峰的高度不等,實現了近似同步。
4 基于dSPACE的分數階光敏神經元實現
本文利用時域-頻域轉換法,構建分數階積分器,對模型進行分數階求解。然后采用dSPACE工作平臺(如圖10)對Simulink輸出信號經比例縮放驗證分數階光敏神經元的動力學行為,其中系統參數變化對動力學特性的影響如圖11-圖14所示,分數階光敏神經元的耦合同步如圖15所示。

圖10 基于dSPACE的工作實驗平臺
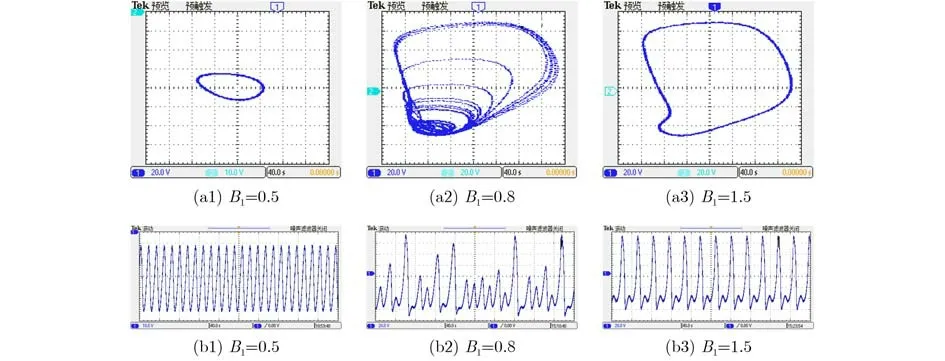
圖11 q=0.99時參數B1取不同值時的相圖及時間序列圖

圖12 q=0.9時參數B1取不同值時的相圖及時間序列圖
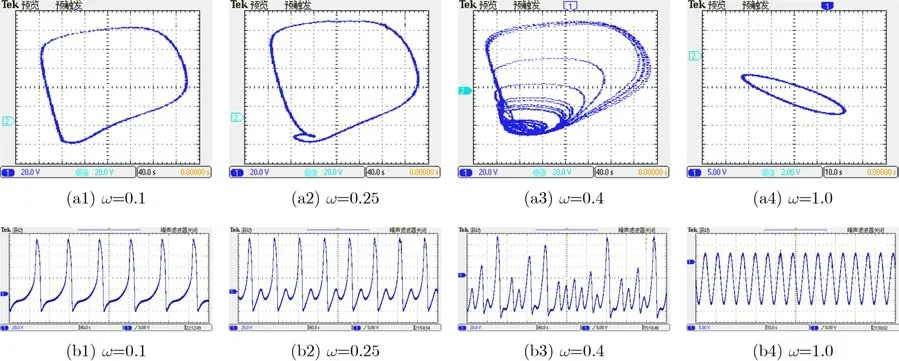
圖13 q=0.99時參數ω取不同值時的相圖及時間序列圖
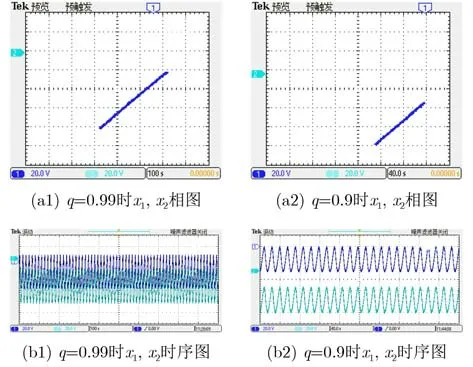
圖15 光敏神經元不同階次對初值的同步
5 結束語
本文在整數階光敏FHN神經元電路中引入分數階微積分理論,提出了分數階光敏神經元模型。通過分岔分析,光電流的改變可以誘發系統豐富的放電模式,如周期放電、尖峰放電和混沌放電狀態。綜合分析結果表明,分數階光敏神經元系統對相同的外部信號表現出更多的周期性放電區域,隨著分數階階次的降低,分數階系統的混沌區域減少,光敏神經元的活躍度增加,對外界信號的適應能力增強。數值仿真和dSPACE實現結果表明,當選取不同的系統參數時,神經元系統在周期放電和混沌放電狀態之間轉換;當參數選取不同值時,系統可以誘發周期放電、混沌放電、尖峰放電等不同的放電模式。此外,使用電突觸耦合的方式連接兩個分數階光敏神經元,并通過調整耦合系數來實現神經元之間的相位同步和完全同步。結果表明,分數階神經系統具有較強的信息編碼和傳輸能力,對進一步研究功能性神經電路與神經網絡的應用具有一定的借鑒意義。

