設計參數不確定條件下滾動直線導軌運動性能分析

李云峰

(三江學院機械與電氣工程學院,南京 210012)

0 引言

滾動直線導軌具有定位精度高、摩擦系數小、精度保持性好、可維護性好等優點,因此在主軸系統和進給系統中廣泛應用,已經成為了數控機床重要的功能部件[1-2]。直線導軌的運動特性直接影響到產品的加工精度和質量,因此研究滾動直線導軌的動態運動性能具有重要的意義[3-4]。

影響滾動直線導軌動態運動性能的因素很多,一般從摩擦、磨損、預緊力和裝配誤差等方面開展研究工作。YI等[5]通過研究摩擦對導軌微觀和宏觀的動態特性的影響規律,對直線導軌位置精度進行了研究工作。ZOU等[6]研究了直線導軌在使用過程中由于摩擦和磨損的影響而引起的接觸剛度變化,建立導軌接觸剛度預測模型。TAO等[7]建立了滑塊滾道磨損引起的位移計算模型,對直線導軌的磨損和性能進行預測。梁醫等[8]分析了滾道中心距不同誤差情況下對滾動直線導軌承載能力的影響規律。KONG等[9]綜合考慮預緊力、初始接觸角和球徑等因素的影響,研究了線性導軌的動態特性和穩定性。

但是,在實際工程中,由于不能完全消除參數的隨機性,不可避免地存在如材料性能、幾何尺寸、載荷等著不確定因素,導致了直線導軌運動特性的不確定性[10]。針對此問題,WANG等[11]利用正太分布表征幾何參數的不確定性,采用隨機攝動法計算動態誤差的統計矩,實現對直線導軌動態運動性能的分析。然而,由于工程問題的復雜性和樣本數量的限制,很難得到參數精確的概率分布[12]。假設幾何參數服從特定的概率分布,即使是偏離真實值的微小變化,也可能造成較大的計算誤差[13]。雖然無法準確定義不確定參數的概率分布,但是可以比較容易確定參數的上下界,因此可以用區間模型來處理參數的不確定性[14]。區間分析方法僅需知道不確定參數的上下界,可以更大程度保留參數的原始信息,使得分析計算結果更符合實際情況,因此得到了廣泛的應用[15-16]。

目前,尚未有關于設計參數不確定性對滾動直線導軌運動性能的研究。本文利用區間模型表征直線導軌設計參數的不確定性,通過分析直線導軌實際受載情況并基于Hertz接觸理論,建立了滾動直線導軌二自由度動力學分析模型;然后,利用龍格-庫塔法進行求解,得到各個時刻直線導軌的動態響應值。以SHS-45R系列滾動直線導軌為例,利用本文所述方法對不同精度等級的導軌運動性能進行了分析。

1 直線導軌動力學分析模型

1.1 直線導軌受力模型

直線導軌在實際運行過程中,受到復雜的工作載荷的作用,考慮到實際工作情況,假設直線導軌受到垂直載荷Fy和水平載荷Fx的作用,如圖1所示,并假設Fx和Fy均為簡諧激振力[17]。

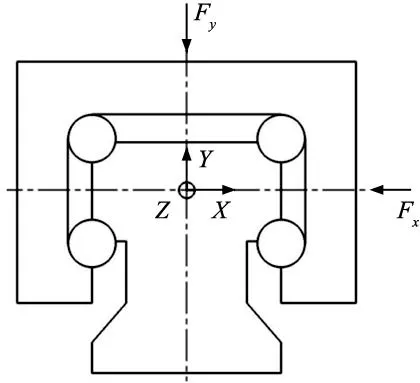
圖1 直線導軌受力分析圖

1.2 直線導軌定位誤差分析

直線導軌精度公差包括行走平行度公差與尺寸公差[11]。如圖2所示,導軌的幾何公差包括M向的公差ΔA以及W向的公差ΔB,通過提高安裝精度可以降低幾何誤差[18]。直線導軌實際工作過程中,由于載荷的作用,產生垂直位移V和水平位移H。由于幾何參數的不確定性,導致滑塊各個時刻V和H的值出現波動,由此造成導軌運動過程中的平行度誤差。

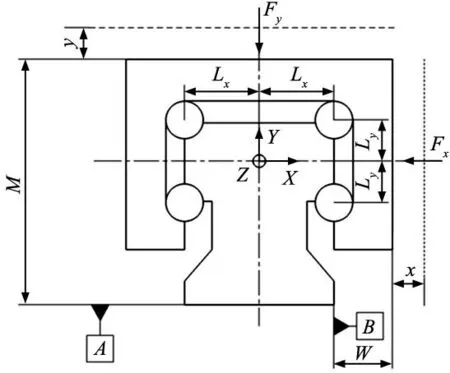
圖2 滾動直線導軌的精度公差

1.3 接觸變形與載荷分析

圖3為直線導軌的結構組成,主要包括滑塊、滾珠和導軌3部分。導軌受到載荷Fy、Fx的作用,因此滑塊產生垂直位移V、水平位移H。4列滾珠編號為i(i=1,2,3,4),第i列滾珠受到的接觸面法向載荷為Qi(i=1,2,3,4)。根據Hertz理論,對滾珠與滾道的接觸進行分析,滾珠與軌道與滑塊接觸模型如圖4所示。Oci和Ori為滑塊和導軌溝槽初始曲率中心,曲率半徑分別為Rc和Rr,通常情況下Rc和Rr相等。

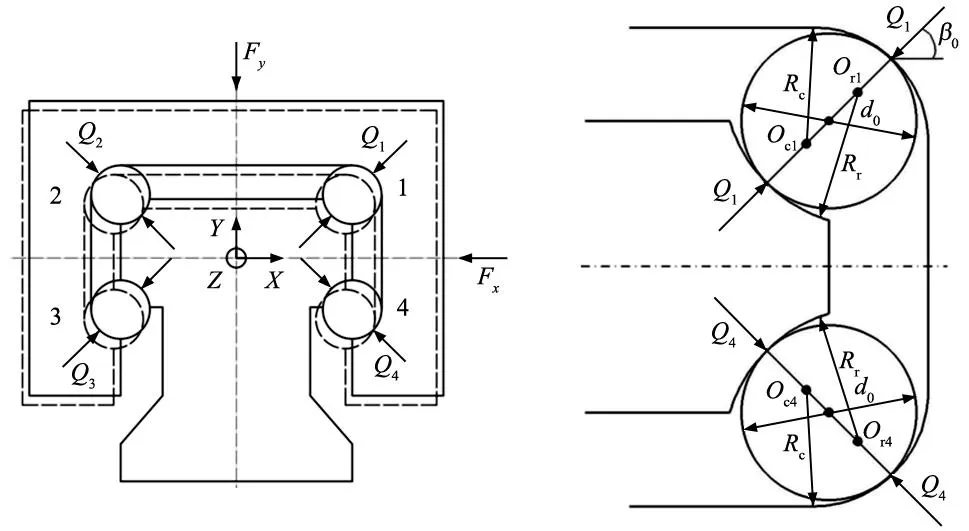
圖3 滾動直線導軌副結構及受力圖

當僅受預緊力P0時,滾珠的初始接觸變形為δ0,通過分析得到Oci和Ori之間的距離s0為:

s0=Rc+Rr-d+δ0

(1)

式中:d表示沒有安裝滾珠時導軌溝槽與滑塊溝槽之間的空間距離,d0為滾珠沒有發生形變時的直徑。在預緊力作用下,滾珠的變形δ0為:

δ0=d0-d

(2)

將滾珠與滾道接觸視為彈性接觸,根據Hertz接觸理論[19],滾珠與滑塊溝槽和導軌溝槽的接觸力為:

(3)

式中:δi為滾珠的彈性變形,v1和v2分別為滾珠和溝槽材料的泊松比,E1和E2分別為滾珠和溝槽材料的彈性模量,μ為與剛度相關的赫茲系數,∑ρ為滾珠與溝槽接觸的綜合曲率。μ、∑ρ可以通過Hertz接觸理論進行計算獲得。將式(3)進行簡化,得到:

(4)

式中:ξ描述了滾珠接觸載荷Qi與彈性變形之間的關系,稱為接觸系數:

(5)

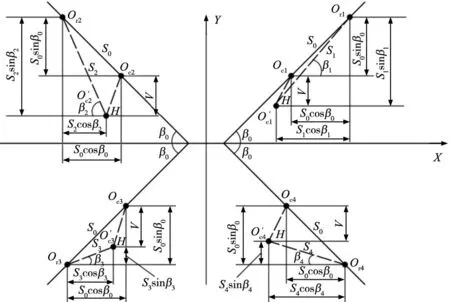
圖5 滾動直線導軌位移與變形的幾何關系

通過分析計算,得到各排滾珠的彈性變形和接觸角表示為:

(6)

(7)

將式(6)帶入式(4),得到滾珠的接觸載荷:

(8)

通過式(8)可知,接觸載荷Qi是關于垂直位移V、橫向位移H的函數。但是,隨著位移的增大,滾珠可能會失去與滾道的接觸,此時接觸載荷Qi會逐漸減少到0,因此接觸載荷V和H的分段非線性函數[11]。直線導軌內部對滑塊總的作用力可簡化為:

(9)

式中:n表示每一排滾珠的數目,FH和FV分別表示導軌內部對滑塊的橫向載荷和垂直載荷。

1.4 直線導軌的動態運動方程

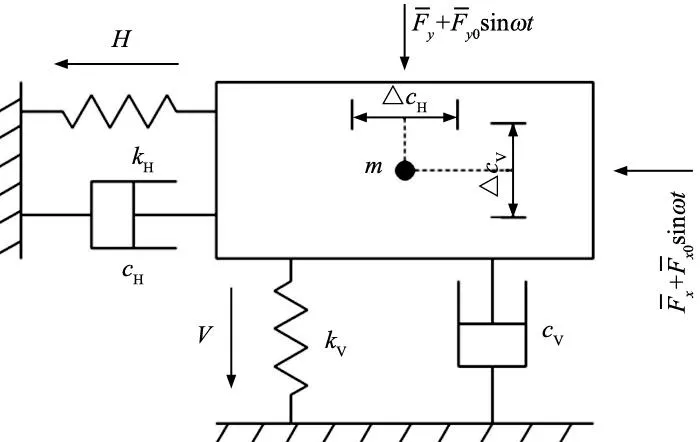
圖6 直線導軌滑塊二自由度動力學模型

由上述分析得到滑塊的動態運動方程為:

(10)

由1.3節對直線導軌的載荷與接觸變形分析可知,滾珠與滑塊的接觸剛度ki是滾珠彈性變形δi的非線性函數[11]。由式(6)可知滾珠彈性變形δi是關于水平位移H和垂直位移V的函數,因此ki同樣為H和V的函數。式(10)中的kHH和kVV分別表示滑塊系統因水平位移H和垂直位移V所產生的接觸載荷,而等效剛度kH和kV為H和V的非線性函數[21]。為了簡化計算,將kHH、kVV兩項分別用滾珠對滑塊的作用載荷進行表示[19]。由式(8)得表達式為:

(11)

將式(11)帶入式(10)得到滑塊系統的動態運動方程:

(12)

由式(12)可知,直線導軌的動力學方程比較復雜,且參數相互耦合,解析求解比較困難,因此利用龍格-庫塔法進行求解,得到各個時刻直線導軌的動態響應值。

2 直線導軌幾何參數不確定分析

本文用區間數對直線導軌的幾何參數的不確定性進行表征,區間數DI是指任意一對封閉有界的實數[14]:

DI=[DL,DU]={D|DL≤D≤DU}

(13)

式中:上標L和U分別表示區間數的下限和上限。

區間數的中點Dc和半徑Dw表示為:

(14)

因此,區間數還可以表示為:

DI=Dc+[-1,1]Dw

(15)

直線導軌動態性能受多個幾何參數的影響,包括初始接觸角β0、滾球直徑d0、凹槽曲率rc和初始變形量δ0[11]。由于直線導軌零部件尺寸公差的存在以及在制造裝配過程的隨機因素影響,幾何參數具有不確定性。因此,利用區間模型表示結構參數的不確定性。假設幾何參數的不確定度為η,因此上述幾何參數的取值區間為:

(16)

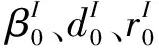
3 算例分析

3.1 直線導軌模型

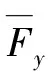
3.2 直線導軌動態響應分析

當各個設計參數在理想值時,采用文獻[11]中的載荷條件,利用第2節中建立的動態模型計算滾動直線導軌的單自由度動態響應。圖7為本文模型計算的直線導軌單自由度的動態響應值與文獻[11]的對比結果。

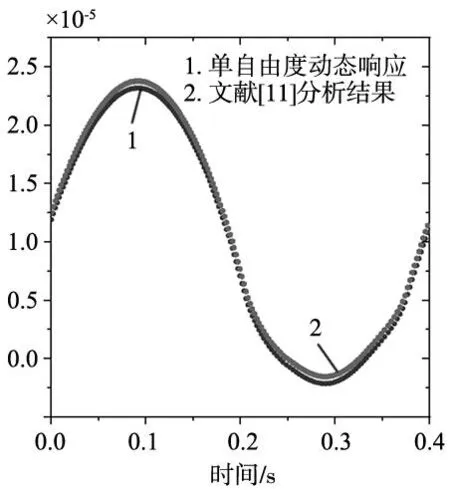
圖7 動力學模型分析結果對比

從圖7可以得到,在相同的載荷條件下,直線導軌垂直方向的動態響應結果基本一致。因此本文所建立的直線導軌動態分析模型的計算精度滿足分析要求。

接下來,分別利用本文所建立的二自由度動力學分析模型對直線導軌的動態特性進行分析,得到了直線導軌的垂直位移和水平位移的動態響應。假設直線導軌幾何參數[β0,d0,rc,δ0]的不確定度η=0.02,因此由式(16)可以得到幾何參數的區間值。在幾何參數區間分布情況下,通過二自由度動力學分析模型,得到直線導軌水平方向和垂直方向的動態位移響應。如圖8所示,直線導軌水平位移和垂直位移的最大值、最小值以及理想值的分布情況,其中,圖8a和圖8b分別表示水平位移和垂直位移。對每個時刻,位移的最大值和最小值位于理想值的兩側。當直線導軌的精度等級為高精度時,其行走平行度公差為3 μm,從圖中可以得到在一個運動周期中,直線導軌水平位移在公差范圍之內約占運動周期的20%(其中上邊界為32.5%,下邊界為20%,取綜合有效值20%),而垂直位移在公差范圍之內約占運動周期的50%。

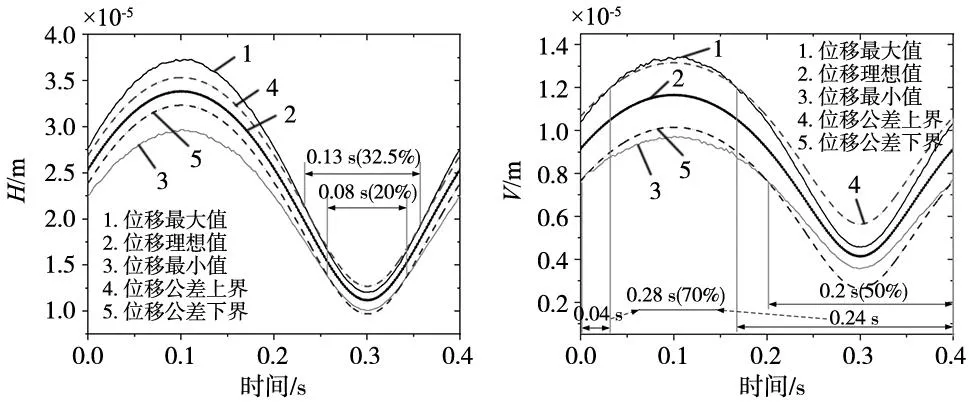
(a) 水平位移特性 (b) 垂直位移特性

由直線導軌受力情況可知,垂直方向載荷大于水平方向載荷,但是從圖8可知,直線導軌水平方向的位移大于垂直方向,而且水平方向位移波動較大,一個周期內運行在公差范圍之內的時間占比較小。主要原因是,由于垂直載荷的作用,第3列和第4列滾珠與滾道接觸狀態發生變化(圖3所示),導致水平方向的等效剛度變小,而垂直方向等效剛度變大。

滾動直線導軌根據運動精度等級的不同,分為普通精度級、高精度級、精密級等,對應的行走平行度公差分別為5 μm、3 μm、2 μm。利用文中所述方法分別評估直線導軌的動態特性,導軌綜合運動特性如表2所示。在相同載荷下,隨著直線導軌精度等級的提高,允許的行走平行度公差逐漸減小,直線導軌水平方向和垂直方向運行在公差范圍之內的時間占比逐漸減小。

表2 不同精度直線導軌運動性能

4 結束語

本文提出了一種考慮幾何參數不確定性的直線導軌運動性能分析方法。根據直線導軌的精度等級確定了運動響應的合理范圍。分析直線導軌實際受載情況,基于赫茲接觸理論,建立了考慮直線導軌接觸特性和結構力學特性的二自由度動力學模型。

為了提高運動性能分析的準確性,用區間模型表示幾何參數的不確定性。通過滾動直線導軌的兩個方向的動態位移響應范圍與運動誤差范圍的對比,得到了滾動直線導軌水平方向和垂直方向上動態位移位于運動公差合理區間內的時間占比。隨著導軌精度等級的提高,兩個方向上動態位移位于運動公差合理區間內的比例越來越小。

本文分析結果對于滾動直線導軌的設計、制造以及實際生產過程中的選型都具有重要的指導意義。但是,也存在不足的地方,比如滾動直線導軌受到負載載荷作用時會產生偏轉、俯仰等運動特性。因此,未來將根據導軌受力情況,建立三自由度、四自由度或五自由度的動力學分析模型,實現對滾動直線導軌運動性能更加準確的分析。