基于改進FNN-BP網絡的304不銹鋼薄板焊接質量推斷模型*

文德沐,胡曉兵,張雪健,毛業兵,陳海軍

(1.四川大學機械工程學院,成都 610065;2.四川大學宜賓園區,宜賓 644000)

0 引言

隨著機器視覺、智能控制、機器學習等新興數字與信息化技術的飛速發展,激光焊接機器人智能化和自動化升級改造也出現了新的發展思路,首先,以各種傳感器和工業相機為基礎的激光焊接焊接過程控制的改造升級[1]。目前,應用最為廣泛的焊接狀態的獲取方式就是基于工業相機的焊接工件圖像采集。基于采集到的圖像,人們可以準確識別焊縫位置并提取特征。激光焊接機器人視覺系統,因其使用方式簡單、數據易于處理等優點,是激光焊接焊縫識別和焊縫追蹤技術的研究熱點;其次,是以專家系統和模糊推斷為基礎的焊接工藝控制智能升級[2]。

傳統的焊接工藝,絕大多數是基于人工經驗與工程手冊獲得的[3]。因此,激光焊接機器人智能化改造的重要一個環節就是如何讓機器人具有人的“經驗”,并可以基于這種“經驗”完成焊接工藝的推定。而以視覺系統和各種類型的傳感器為引導,以神經網絡、模糊控制和專家系統等技術為決策核心的新型智能焊接控制系統以逐漸成為了發展的重點[4]。該種方案,可實現完全的焊接機器人自主作業而最大程度減少人工干預和主觀干擾[5]。因此,基于提出的激光焊接機器人智能化和自動化改造方向[6],搭建出一套基于機器視覺、神經網絡和模糊控制的智能激光焊接機器人系統,對我國激光焊接機器人的智能化和自動化改造提供了新的設計思路和發展方向,具有很強的實際意義。

通過調研,發現常見的焊接質量的評估分為兩種:一類是以傳統的破壞性或機器檢測方式對焊接件焊縫進行檢測,該種檢測方式需要較長的周期,同時也較為浪費人力、物力和財力,一般情況下只會在月度檢查或抽檢中使用;另一種方式就是生產技術人員目視檢測,通過肉眼或一些觀測儀器通過分析焊接件的焊縫圖像特征去人為依靠于人工經驗去判定該種工藝的焊接質量,該種方式具有很強的主觀性和經驗主義,無法進行復現和標準化表達。本文從實際應用場景出發,對304不銹鋼的激光焊接質量評價提出了一種新的質量評價標準和實現方案,并建立一個完整的304不銹鋼薄板激光焊接質量評價體系。

基于該建立的激光焊接質量評價標準和焊接工藝參數與焊接質量之間的影響關系,本文建立了一個激光焊接質量推斷專家系統模型[7-8],該模型可以通過輸入激光焊接工藝參數,智能推斷該工藝參數帶來的激光焊接質量,進而簡化焊接工藝的選擇和優化過程。為實現激光焊接質量的智能預測,本文采用模糊推斷[9-10]、改進專家系統[11-12]和BP神經網絡[13]相結合的方法,基于焊接規律對304不銹鋼激光焊接質量進行推斷,然后通過仿真實驗驗證該推斷系統的準確性。

1 質量評價體系

將焊縫圖像的評價標準數值化時,采用表1所示規則。

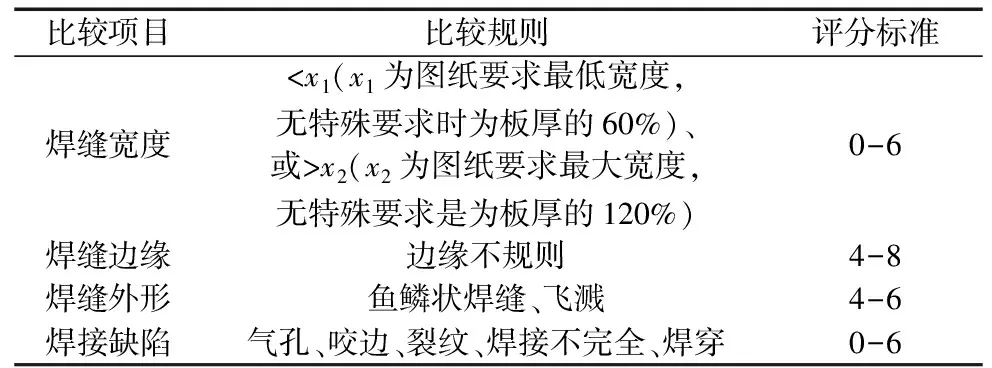
表1 焊縫圖像質量評分規則

對焊接件平面度的質量評價主要就是對焊前母材和焊后焊接件的平面度差值Δx。

2 智能推斷模型的搭建

2.1 系統整體方案

本文基于板材厚度、焊接速度、焊接功率、離焦量、占空比和峰值功率設計304不銹鋼焊接質量智能推斷模型,該模型的輸出預測參數為平面度和焊接質量評分,預測系統整體結構流程如圖1所示。

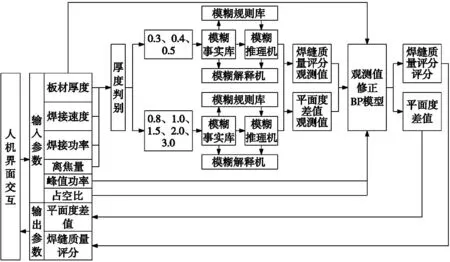
圖1 預測系統整體結構

預測方案的實現過程為:

步驟1:數據分類。對實驗測試數據進行分析,匹配,然后基于匹配結果,人為將板材按照厚度劃分為“薄板”,即板材厚度為0.3 mm、0.4 mm、0.5 mm,和“厚板”,即板材厚度為0.8 mm、1.0 mm、1.5 mm、2.0 mm、3.0 mm,然后基于兩類板材厚度建立不同的模糊規則庫和模糊推斷模型;

步驟2:模糊預測。基于焊接速度、焊接功率和離焦量3個輸入參數對于焊縫圖像質量評分和焊接件平面度差值的影響,采用TSK模糊系統,建立各厚度下各輸入參數的隸屬度函數與模糊規則庫,進而基于模糊規則庫推斷焊接件平面度差值和焊縫質量評分的觀測值;

步驟3:預測值修正。本文基于板材厚度、峰值功率、占空比和觀測值,建立了一個BP神經預測網絡,通過該網絡實現焊接質量預測值對不同板材厚度、峰值功率、占空比的修正與補償,以提高預測準確性。

2.2 模糊推斷模型

本文采用模糊系統去對該種“經驗”進行數字化建模,采用三輸入-二輸出的Takagi-Sugeno系統搭建焊縫質量評分與平面度差值推斷模型,如圖2所示。

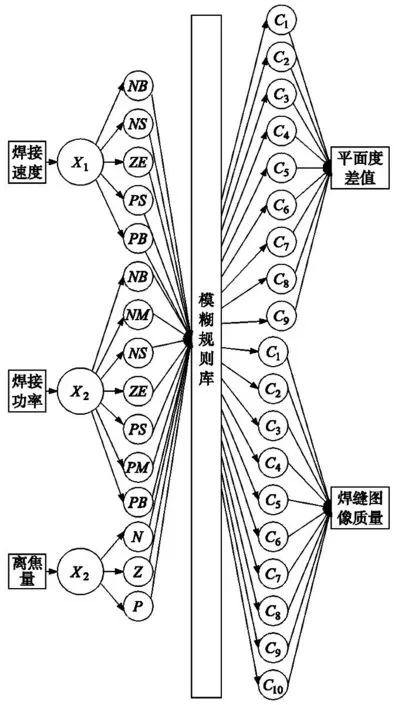
(a) 薄板類

2.2.1 隸屬度函數設計

本文對兩個厚度等級下不同的模糊推斷系統的輸入參數進行單獨的論域取值和模糊子集設定,輸入參數論域和模糊子集如表2所示。

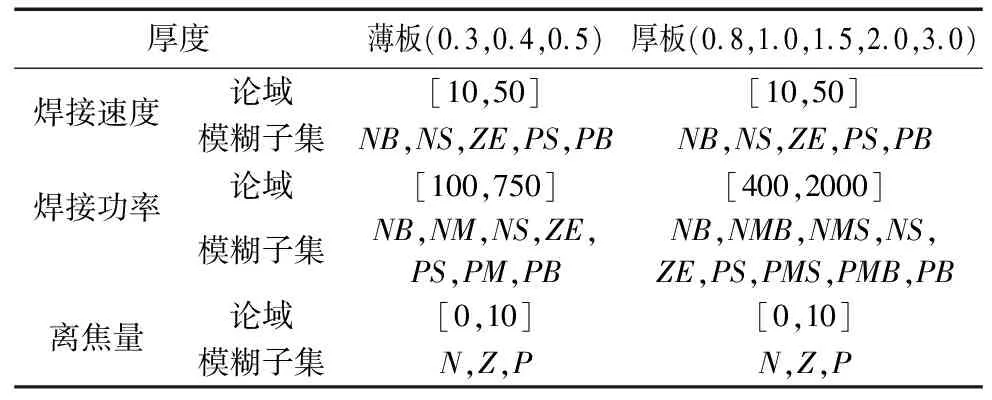
表2 輸入參數論域及其模糊子集

其隸屬度函數,如圖3所示。

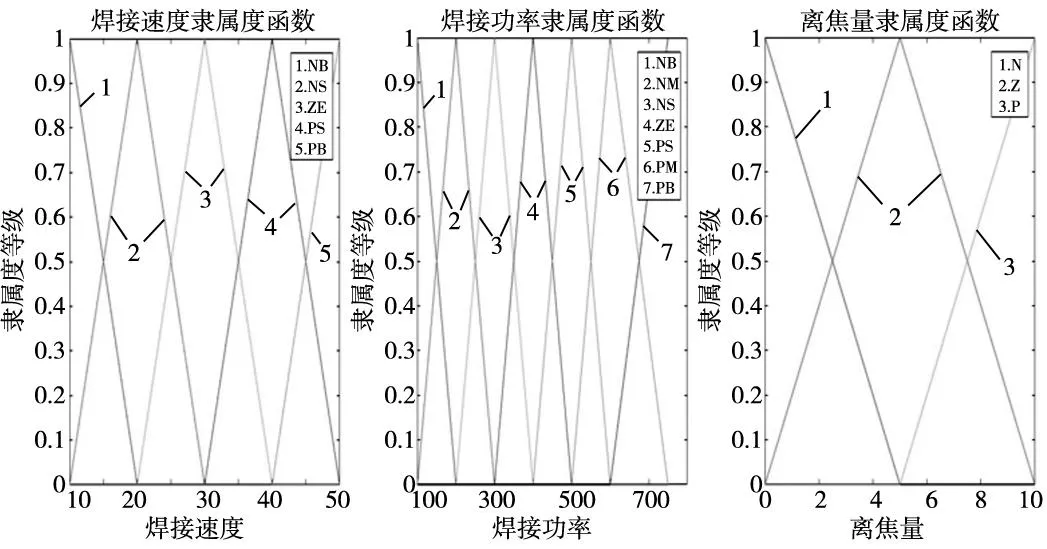
(a) 薄板類零件

對于輸出參數而言,采用TSK單值輸出的方式直接輸出推斷值。

通過實驗測定和資料查閱,本文將焊縫質量評分的預測輸出值設定為0～9級,共10個等級,其中1～9級分別代表著焊接質量從1～9,即從差到好,而0級代表著未完成焊接過程。而對于焊接平面度而言,本文對實驗數據中不同厚度的平面度差值取值經過分析和計算后,為兩個厚度等級設定不同的平面度差值取值。對“薄板”,將其設定為1～9級,其中,1～8級分別代表著最大平面度差值為0.3、0.5、0.8、1.0、1.2、1.5、2、3 mm,而9級取值為-1,代表著未完成焊接。對“厚板”,將其設定為1～12級,其中1～11級分別代表著最大平面度差值為0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.5 mm,而12級取值為-1,代表著未完成焊接。

2.2.2 模糊規則設計

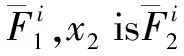
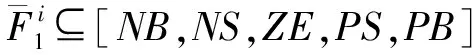
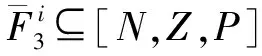
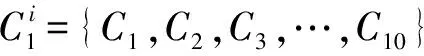
對“薄板”,模糊系統一共有5×7×3=105條。

因此通過上述的模糊規則庫,可以將不同厚度條件下的焊接速度、焊接功率、離焦量和焊縫質量評分和焊接件平面度差值進行匹配和對應。進而可以通過隸屬度函數的不同,去匹配不同的模糊規則,實現由前件事件(焊接輸入參數)到后件事件(焊接質量評價)的模糊推斷。

2.2.3 解模糊化

通過比較各解模糊化方法的準確性和計算量,選擇面積重心法進行模糊的解模糊化[14]。面積重心法取的μC(z)加權平均值為z的準確值,即:

(1)

當取值論域為離散域時,

(2)

最后根據上文設計的模糊推斷系統工作流程,分為薄、厚板分別輸入去解模糊化。

2.3 預測值修正模型

除了焊接速度、焊接功率、離焦量3個主要參數外,板材厚度、峰值功率、占空比這3個參數對焊接質量也有較大影響。因此,本文基于上述3個參數,分別建立“薄板”和“厚板”條件下,由模糊推斷模型獲得的焊接焊縫質量評分觀測值和平面度差值觀測值到實際輸出的焊縫質量評分預測值和平面度差值預測值的修正BP神經網路模型,如圖4所示。

圖4 模糊預測值BP修正模型

上述4個模型,其BP神經網絡采用“1-1-1”的結構,即一層輸入層、一層隱含層和一層輸出層,每一層都與下一層全連接。

輸入層4個參數x=(x1,x2,x3,x4),x1為模糊系統輸出觀測值,x2為板材厚度,x3為峰值功率,x4為占空比。

輸出層1個參數y,y為修正后預測值。

由Kolmogorov定理可得,由于輸入層有4個節點,輸出層有1個節點,因此中間層隱含節點個數滿足下列關系式:

(3)

即通過分析,上述4個BP模型中間層隱含個數分別為12,12,13,13。

對上述4個模型,隱藏層結果和輸出層結果可由下式表達,即:

(4)

(5)

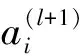
該網絡采用反向傳播算法更新參數,首先計算損失函數J(θ),然后再逐層反向求出損失函數J(θ)對各層的偏導數,采用梯度下降的算法更新網絡,輸出層參數更新算法為:

(6)

(7)

(8)

(9)

式中:J(θ)表示BP神經網絡的損失函數,yi為網絡輸出,α為學習速率。

2.4 模型仿真分析

基于上文建立的模糊推斷模型和預測值修正模型,本文使用MATLAB數據處理軟件對該模型進行建模分析,測試并驗證本文提出的激光焊接質量智能推斷模型的可靠性[15]。

2.4.1 模糊系統建模

基于MATLAB中的設定參數和上文設定的隸屬度函數,本文建立了薄板和厚板的模糊模型,如圖5所示。

(a) 薄板

2.4.2 神經網絡建模

本文基于MATLAB建立上述4個BP參數修正模型,基于上述設定參數和已有實驗數據,本文分別訓練了4個BP模型,其訓練準確率如圖6所示。

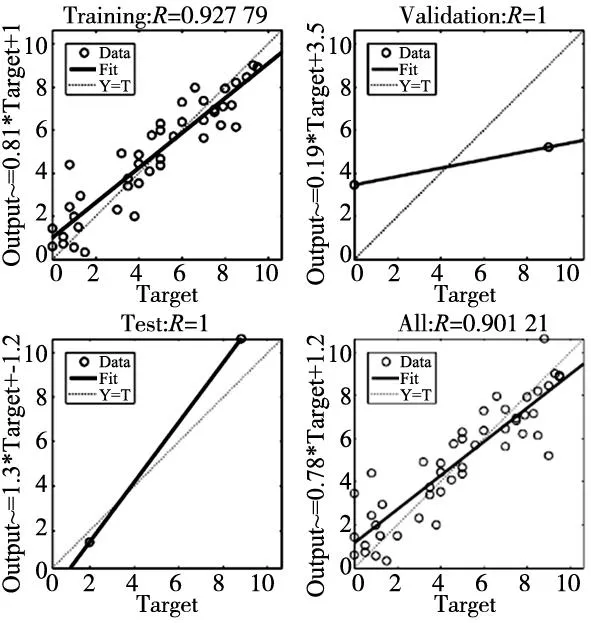
(a) 薄板焊縫質量評分預測值修正模型

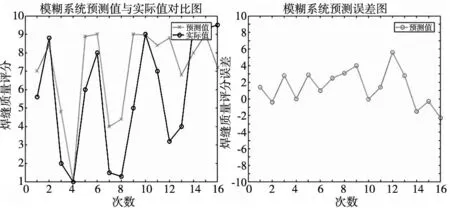
(a) 模糊系統預測0.5 mm不銹鋼板材焊縫質量評分對比圖及其誤差圖

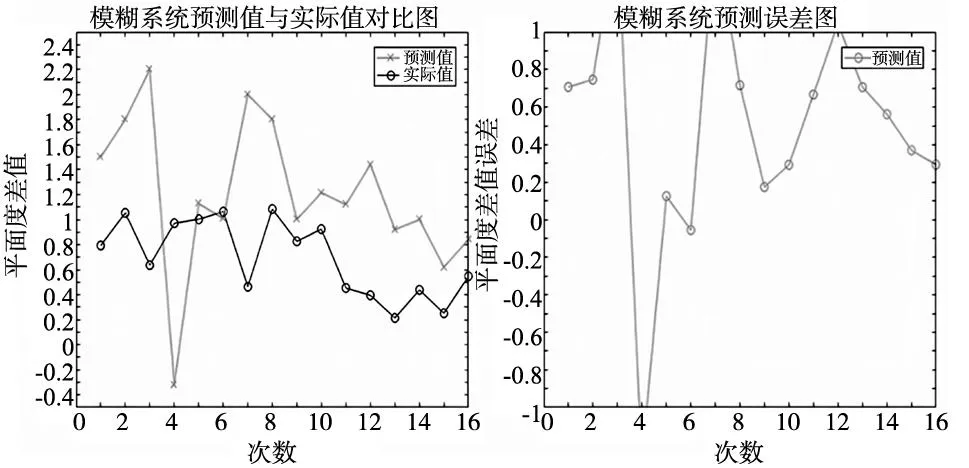
(a) 模糊系統預測0.5 mm不銹鋼板材平面度差值對比圖及其誤差圖

2.4.3 模型對比仿真

基于上文建立的模糊推斷模型和預測參數修正模型,選擇0.5 mm厚度的304不銹鋼進行焊縫質量評分和平面度差值進行無修正模型和有修正模型的預測。

(1)焊縫質量評分

(2)平面度差值

2.4.4 模型仿真分析

對焊縫質量評分、平面度差值預測進行誤差分析,如表3和表4所示。

表3 焊縫質量評分模型誤差分析

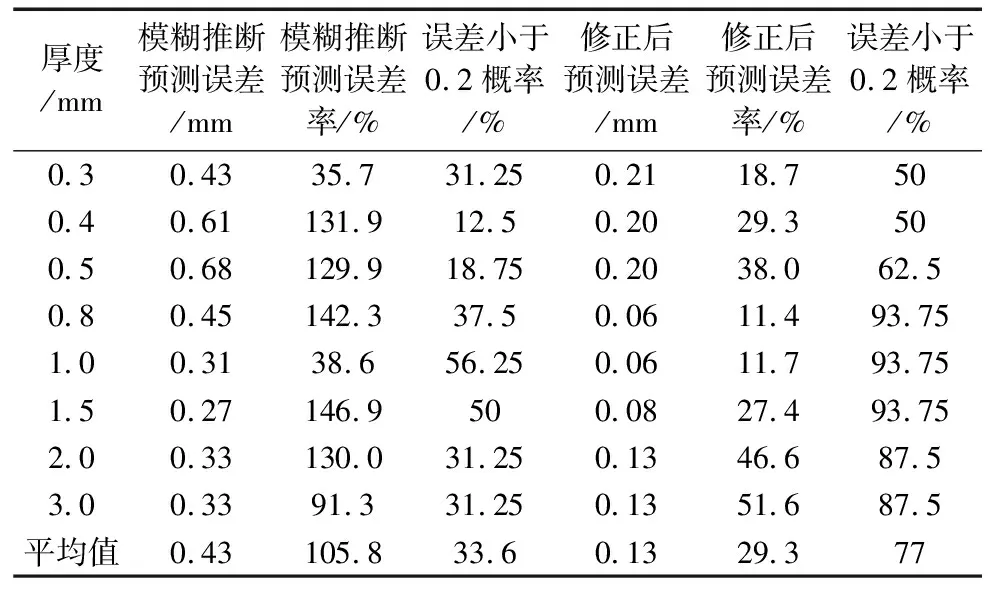
表4 平面度差值模型誤差分析

對304不銹鋼板材激光焊接的焊縫質量預測進行分析,可得:

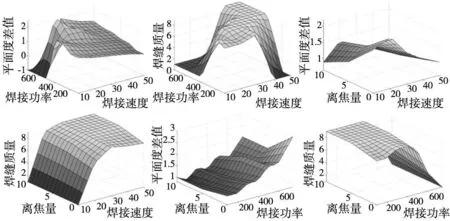
(1)對于由焊接規律建立的焊接件焊縫質量模糊推斷模型而言,其平均預測誤差為2.51,平均誤差率為113.7%,平均預測準確性僅為39.8%(誤差小于1),最大預測誤差為4.44,最大誤差率為241.2%,其預測較為準確的概率為18.75%。雖然其并無法在所有厚度條件下獲得較好的預測效果,但是其在厚度為0.5mm、2.0mm、3.0mm以及其他厚度的部分取值下也可以獲得較為準確的焊接件焊縫質量預測值,由此可得得出,雖然由于模糊系統隸屬度函數設計和規則設計的不準確,導致模糊推斷存在誤差,但是通過圖表可知該預測在一定程度上符合已有的304不銹鋼焊接中焊接質量與焊接參數的對應關系,其預測具有一定的可行性。

(2)對比直接由模糊推斷獲得的焊接件焊縫質量評分預測值,經過BP修正模型修正后,焊接件預測值的準確性大幅提高,其平均誤差降為0.88,平均誤差率降低82.4%,為31.3%,此外修正后預測值的突變概率和極值可能性大大降低,最大誤差降為1.19,最大誤差率也降為56.7%。此外,對于預測準確性而言,對于所有厚度其平均有67.2%的預測準確性,而對于部分厚度而言,其均有70%以上的預測準確性。由此可知,經過該修正模型修正后、焊接件焊接質量的預測基本可以符合準確性要求。

對304不銹鋼激光焊接焊接件平面度差值預測模型進行分析,可得:

(1)對于由焊接規律建立的焊接件平面度差值模糊推斷模型而言,其平均預測誤差為0.43,平均誤差率為105.8%,平均預測準確性僅為33.6%(預測誤差小于0.2),最大預測誤差為0.68,最大誤差率為146.9%,最小預測準確的概率為12.5%。由于板材較薄時平面度變化較為嚴重,因此該模糊推斷模型在“薄板”條件下的預測效果較差。但是當板材厚度增加時,平面度差值變化率降低,其在“厚板”條件下可以獲得較為準確的預測效果,即預測誤差在0.3左右。由此可以得出,由于焊接件平面度變化規則較為復雜,且模糊系統隸屬度函數設計和規則設計的準確性不夠,導致模糊推斷存在誤差,而這種誤差單純使用隸屬度函數增加、模糊規則數增加等方式無法實現較好的改善。但是通過圖表可以看出,該模糊預測模型在變化趨勢和部分取值上具有一定的可靠性。因此,其在一定程度上符合已有的304不銹鋼焊接中焊接質量與焊接參數的對應關系,其預測具有一定的可行性。

(2)對比直接由模糊推斷獲得的焊接件平面度差值預測值,經過BP修正模型修正后,焊接件預測值的準確性大幅提高,其平均誤差降為0.13,平均誤差率降低76.5%,為29.3%,此外修正后預測值的突變概率和極值可能性大大降低,最大誤差降為0.21,最大誤差率也降為56.7%。此外,對于預測準確性而言,對于所有厚度其平均有77%的預測準確性,而對于部分厚度而言,其均有93.75%以上的預測準確性。由此可知,經過該修正模型修正后、焊接件平面度差值的預測基本可以較好符合準確性要求。

3 結論

本文將已有的激光焊接人工經驗進行分類歸納和總結,并結合相關資料和數據,基于模糊專家系統提出了焊接參數的到焊接質量的推斷模型,建立輸入參數的隸屬度函數和模糊規則庫。由于板材激光焊接的復雜性,焊接數據離散化嚴重,無法使用單一模糊推斷模型進行準確預測,因此本文根據板材厚度、峰值功率和占空比與焊接質量的關系,建立了模糊推斷值的BP神經網絡修正模型。通過模型將模糊推斷值進行修正,進而獲得較為準確的焊接質量預測。基于上述研究,本文認為使用神經網絡、模糊推斷、專家系統等新興計算機技術,可實現一定程度上模擬人腦的邏輯思維與判斷,進而可以將傳統機械加工制造業中絕大多數人工經驗型工作進行機器替代,包括焊接、打磨等。該種機械替代方式,不僅保留著人工經驗在作業過程中的優點,而且充分發揮了計算機技術的優勢,真正做到了“兩全其美”,該人工與機器結合的方式,在制造業發展轉型過程中也必將起到重要作用。