水工隧洞礦山法爆破參數設計及對臨近隧洞的影響
楊 東,符 龍,方 超
(云南省滇中引水工程有限公司,昆明 650000)
0 引 言
傳統礦山法施工因其技術成熟,在水工隧洞工程的施工中得到廣泛采用。根據勘察設計和計劃發揮的作用,水工隧洞通常采用雙洞設計,在確定好施工位置后,一般采用一前一后的施工方式;后續施工的隧洞,采用礦山法進行鉆爆施工過程中,由于爆破振動,在不同程度上對已施工隧洞產生影響。因此,對施工參數效果評估和影響研究具有重要意義。
為此,許多學者進行了相關研究。林大超等[1-2]基于對爆炸波在空氣中傳播的方式以及對空氣產生的壓縮波,改進了爆炸時爆炸波在傳播的超壓函數,提出了新的超壓函數修正計算公式。楊軍等[3-4]采用高速攝影手段,對爆破過程中巖土中的裂紋分布進行了試驗研究,結果表明,采用柱狀裝藥爆破,在爆破時,巖體中的裂紋將隨時間而不斷延展,呈現出規律性變化特征。盧文波等[5-6]對爆破后布置炮孔位置處徑向裂紋尖端的應力集中效應進行了定量評估和計算,對爆破裂紋的擴展階段進行了劃分,結果表明,爆破后徑向裂紋擴展主要分為兩個階段,即穩定階段和間斷擴展階段。
上述文獻主要針對在爆破時,孔徑大小和孔內應力集中現象和裂紋擴展情況進行了研究,并得出相應規律,而較少采用數值模擬軟件,研究雙洞隧道施工中爆破對另一隧洞的影響。因此,本文利用ANSYS/LS-DYNA軟件,構建模型,通過設計不同的裝藥量,研究爆破振動對已建水工隧洞的安全性影響。
1 幾何模型
本文以雙洞設計形式的水工隧洞礦山法施工為研究背景,隧洞的幾何外部邊界尺寸為43.1m×6m×20.5m,隧道拱頂距離上邊界為5m,隧道拱底距離下邊界為5m,左側待建水工隧道的左邊界距離模型左邊界為5m,右側已建水工隧道的右邊界距離模型的右邊界為5m。雙洞均設計為拱門形狀,左右兩側隧道尺寸一致,洞寬8m,高9.9m,襯砌厚度0.3m,左右兩側隧道間隔15.9m進行施工,左側待建隧道掘進1m。整體隧洞幾何尺寸見圖1;巖體的物理力學參數見表1。

表1 巖體的物理力學參數
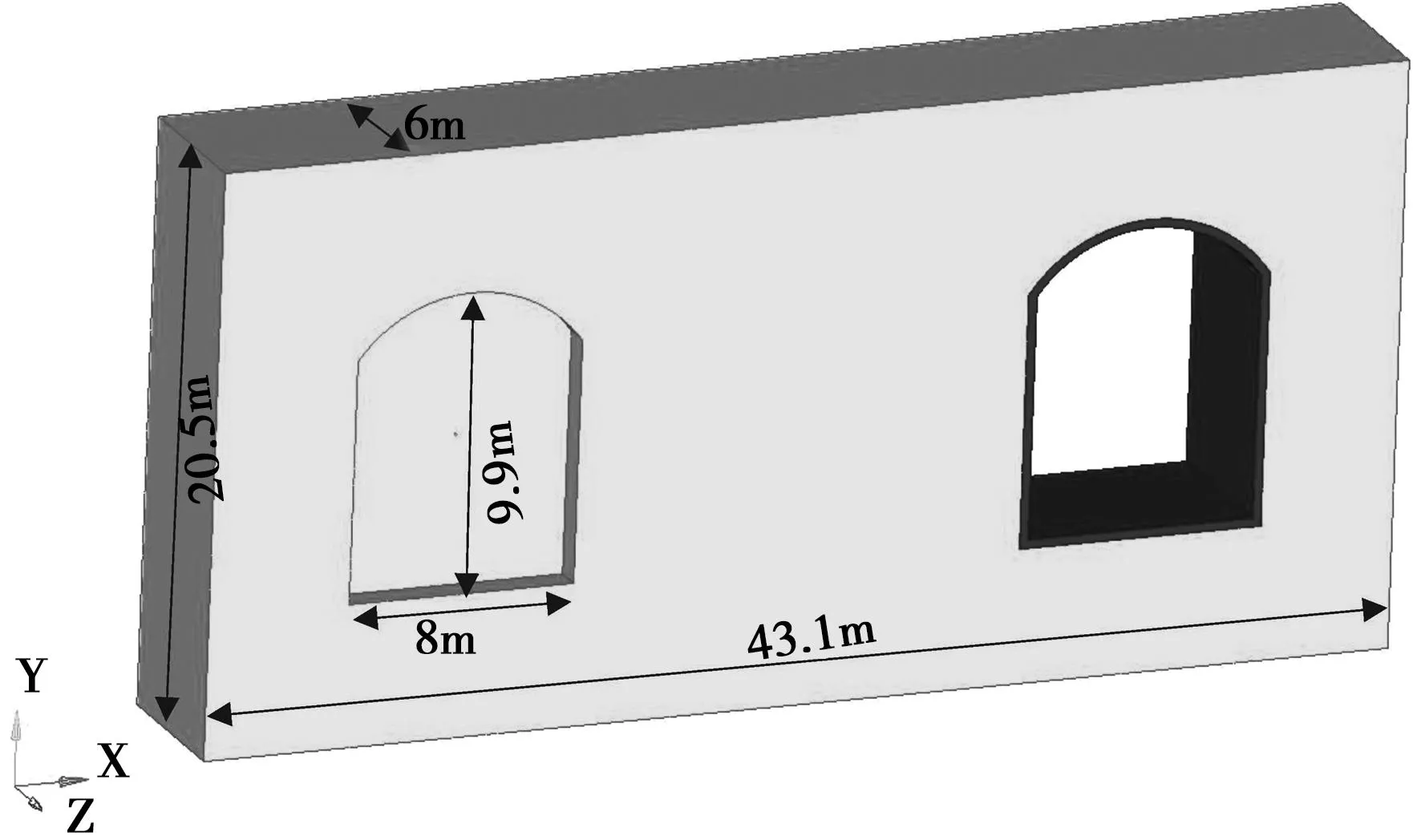
圖1 幾何模型尺寸
2 數值模型建立
采用非線性動力學分析軟件ANSYSLS-DYNA求解器,進行求解分析。首先,在具有良好銜接功能的proe軟件中,根據圖1幾何模型,建立用于計算雙洞設計的水工隧洞幾何模型。然后,將建好的幾何模型通過導入的方法在hypermesh14.0中打開,在hypermesh14.0軟件中對已經建好的幾何模型進行網格劃分,模型見圖2。最后,將模型導出成K形式的文件格式,以便與ANSYSLS-DYNA求解器軟件能夠良好兼容,再采用該軟件對模型進行求解,利用軟件中內嵌的LSPREPOST模塊進行結果輸出和處理[7]。
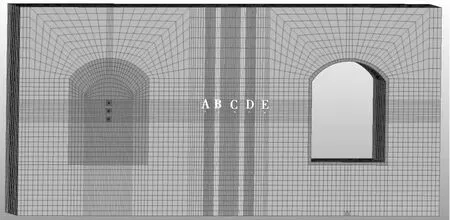
圖2 分析模型圖
3 計算結果分析
3.1 0.5ms應力
為了研究在設計單孔裝藥量2.8kg下爆破后的應力傳播過程,分別對不同峰值時刻的應力云圖進行繪制并導出,得到爆破后0.5ms時刻的應力云圖,見圖3。

圖3 0.5ms應力云圖
由圖3可知,在單孔裝藥爆破后,圓柱形炸藥以近似圓柱狀向四周擴散,由圖3中紅色區域可知,此時的大應力影響范圍較小,僅限于圓柱形炸藥孔周圍區域,這種顯著的瞬時應力集中效應,會造成振動波沿圍巖體的快速傳播和波速的急劇上升,后續振動波速隨著時間的變化曲線可以得到印證。由應力云圖的整體輪廓大小可知,此時的爆炸整體影響范圍也局限于爆炸孔周圍部分,爆炸產生的能量在爆破孔周圍區域迅速產生應力集中效應,在0~0.5ms時間段內圍巖的應力來不及消散,處于能量積聚、應力累積階段。
3.2 8.5ms應力
為了研究在設計單孔裝藥量2.8kg下爆破后的應力傳播過程,分別對不同峰值時刻的應力云圖進行繪制并導出,得到爆破后8.5ms時刻的應力云圖,見圖4。

圖4 8.5ms應力云圖
由圖4可知,在單孔裝藥爆破后,圓柱形炸藥在0~0.5ms時間段內以近似圓柱狀向四周擴散,在0.5~8.5ms時間段內以近似圓形向四周擴散。由圖4中紅色區域可知,此時的大應力影響范圍較0.5ms時刻增大,這一階段屬于應力急劇消散階段,此刻傳播出的振動波沿圍巖體向周圍的傳播速度有所下降,最大波速急劇減小,同樣可以從后續振動波速隨著時間的變化曲線得到印證。由應力云圖的整體輪廓大小可知,此時的爆炸整體影響范圍顯著增大,爆炸產生的能量在爆破孔周圍區域迅速消散,處于能量消散、應力衰減階段。
3.3 59.5ms應力
為了研究在設計單孔裝藥量2.8kg下爆破后的應力傳播過程,分別對不同峰值時刻的應力云圖進行繪制并導出,得到爆破后59.5ms時刻的應力云圖,見圖5。

圖5 59.5ms應力云圖
由圖5可知,在8.5~59.5ms時間段內應力消散范圍不再顯著增大,基本以8.5ms時的外部輪廓為準。由圖5中紅色區域可知,此時的大應力影響范圍與8.5ms時刻相當,在經過0.5~8.5ms的應力急劇消散階段后,這一階段應力消散已十分有限,屬于應力殘余消散階段,此刻傳播出的振動波沿圍巖體向周圍的傳播速度顯著減小,最大波速將遠小于8.5ms時刻,同樣可以從后續振動波速隨著時間的變化曲線得到印證。
3.4 振動速度時程變化
為了研究在設計單孔裝藥量2.8kg下爆破后的應力傳播過程,繪制爆破后圖2中A、B、C、D、E監測點的振動速度隨著時間的變化曲線圖,見圖6。
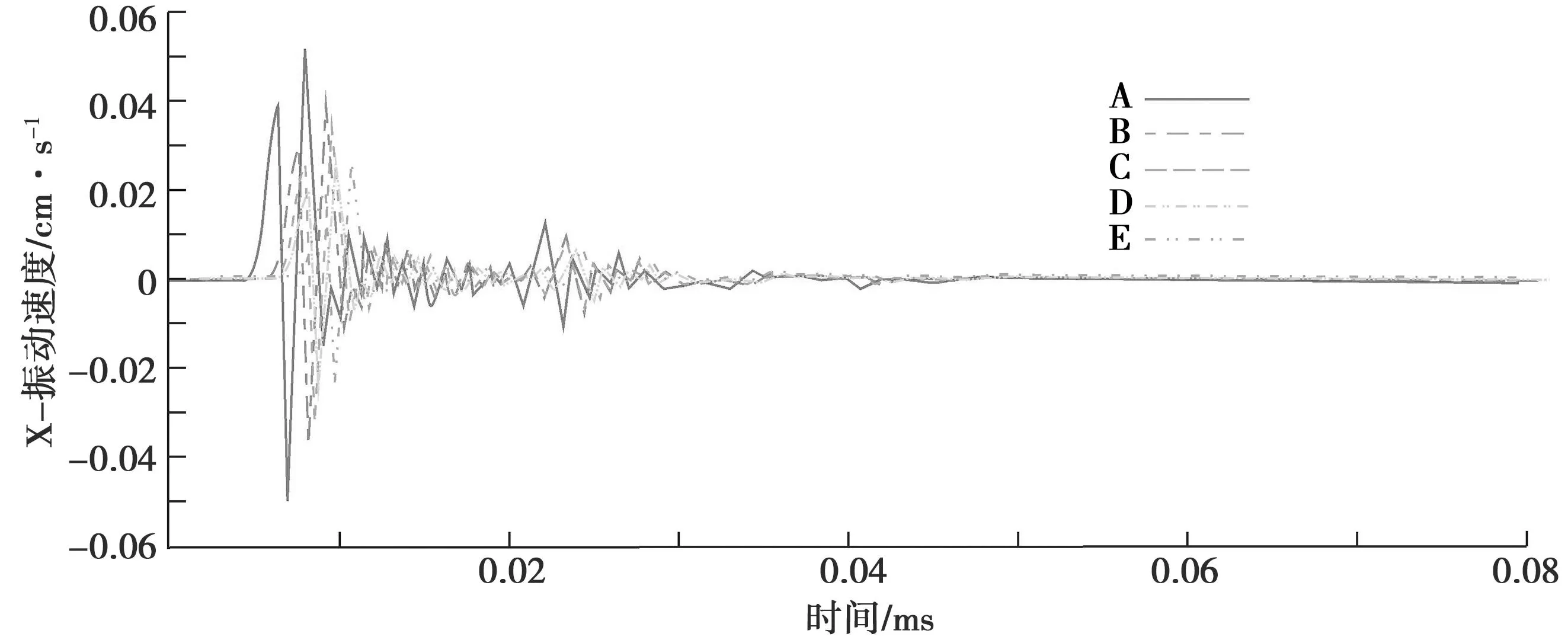
圖6 振動速度時程曲線圖
圖6為5個監測點的最大振動速度隨著時間的變化曲線圖。由圖6可知,距離爆孔不同距離的監測點最大振動速度均表現為隨著時間呈指數形式弱化的趨勢,波長和振幅隨時間均顯著減小。在0.5ms時刻, 5個監測點的振動速度均為最大;在8.5ms時,各監測點的速度峰值明顯減小,顯著小于0.5ms的初值最大振動速度;當達到40ms時,振動速度基本可以忽略。由此可知,在初始時刻時,爆炸產生的應力波急劇擴散,迅速衰減。
3.5 各監測點最大振動速度
為了研究在設計單孔裝藥量2.8kg下爆破后的應力傳播過程,提取A、B、C、D、E監測點的振動速度峰值,并將各監測點處監測到的最大振動速度峰值進行統計,見表2。
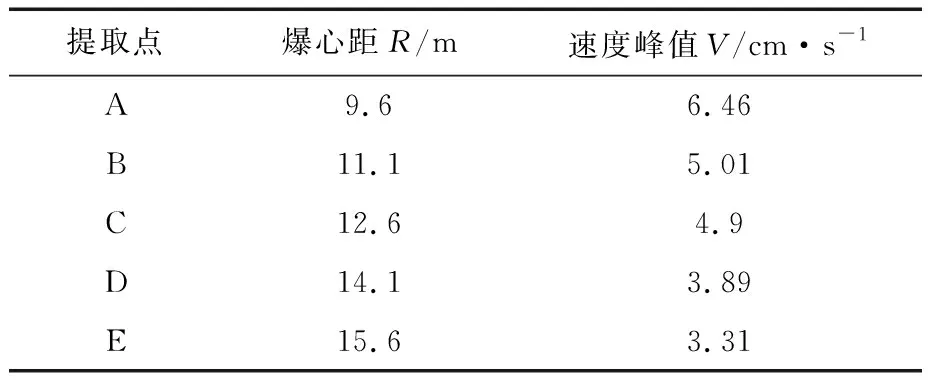
表2 各監測點的最大振動速度值
由表2可知,隨著距離爆孔越遠,最大振動速度越小,當距離相差6m時,最大振動速度差值為3.35m/s,其差值大于E點的最大振動速度3.31m/s。可見,距離爆心的長度大小對最大振動速度具有顯著影響,設計時應考慮設計合理的隧洞間距離,使經濟效益和安全影響的綜合影響達到最優化。由表2還可以看出,盡管各監測點距離爆炸中心的距離間隔均為1.5m,但振動速度的差值并不均勻。因此,在不同距離上,最大振動速度的衰減速率各異,這也為雙洞隧洞間距的選擇提供了有效參考。
3.6 峰值速度變化曲線
為了研究在設計單孔裝藥量2.8kg下爆破后的應力傳播過程,根據表2數據繪制最大振動速度隨爆心距的變化曲線圖,見圖7。
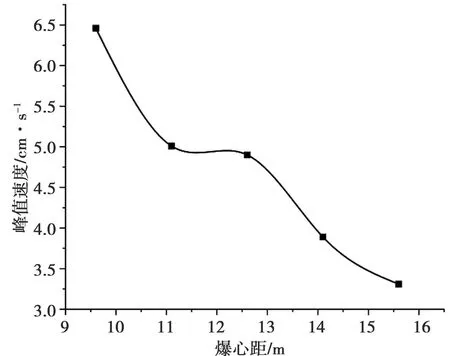
圖7 峰值速度隨爆心距的變化曲線圖
圖7為5個不同爆心距監測點的最大振動速度隨著距離爆炸中心的長度變化曲線。由圖7可知,最大振動速度總體隨著爆心距的增大而不斷減小,當9.6m爆心距增大至11.1m爆心距時,最大振動速度由6.46cm/s減小至5.01cm/s,共計減小1.45cm/s,減小速率為0.97cm/s/m;當爆心距由11.1m增大至12.6m時,速度僅減小0.11cm/s,減小速率為0.07cm/s/m,遠小于第一次增大爆心距時的速率。因此,再次得出在不同距離上最大振動速度的衰減速率各異的結論,為雙洞設計的水工隧洞最優化間距設計和選擇提供了定量依據。
4 結 論
本文以采用雙洞設計形式的水工隧洞礦山法施工為研究背景,進行了數值模擬,結論如下:
1)爆炸能在圍巖體內的傳播經歷了0~0.5ms的能量積聚、應力急劇累積階段,0.5~8.5ms的能量迅速傳播釋放、應力快速衰減階段,以及8.5~59.5ms的殘余能量緩慢釋放、應力殘余消散階段。
2)爆孔距監測點的最大振動速度均表現為隨時間呈指數形式弱化的趨勢,0.5ms時刻振動速度最大,8.5ms時速度峰值明顯減小,達到59.5ms時振動速度幾乎為零,表明初始時段爆炸產生的應力波急劇擴散。
3)最大振動速度總體上隨著爆心距的增大而減小,減小速率在某一爆心距區間內存在極值。本文模型中區間為9.6~11.1m,可為雙洞設計的水工隧洞最優化間距設計提供定量依據。

