優化數學認知結構 提升一輪復習效率
——以“函數零點”復習課為例

福建省浦城縣第二中學 (353400) 黃慧美

一輪復習是高考復習教學的關鍵一環.在此階段,學生依然是課堂的主體,然大多復習課堂卻以教師為主導,延續著“師講生聽”的教學模式,課堂容量大、頻率快,容易出現學生“懂而不會”的尷尬局面.實際上,一輪復習要重視通性通法的提煉,讓解題方法和解題策略更具系統性和方向性,使復習更高效,解題更流暢.本文筆者以“函數零點”復習為例,以典型問題為切入點,引導學生在鞏固基礎知識的同時,掌握解題通法,構建數學思想方法體系,進而優化認知結構,提升復習效率.

一、教學實錄

1.明確方向,激發欲望

A.(0,1) B.(1,2) C.(2,4) D.(4,+∞)

在復習階段,不能將目光定位在解題上,而是要透過題目了解考試動向,分析核心考點,進而進一步鞏固“雙基”,掃清解題障礙.

師:題中涉及到什么概念?

生齊聲答:函數的零點.

師:函數零點的概念大家還記得嗎?

生1:使函數f(x)=0成立的實數x叫函數y=f(x)的零點.

師:很好,那么想一想例1該如何求解呢?

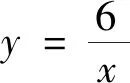
生3:生2的解法沒有問題,解題時既要畫圖又要代值,我覺得這個問題可以換個思路來解,可以考慮應用零點存在的定理來解答.

師:說說你的解題思路.

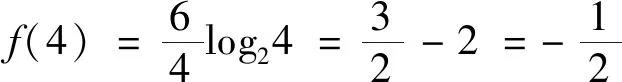
師:很好,通過代數法和幾何法都順利地得到了答案.生2是從定義的角度去考慮,首先將函數零點問題轉化為方程的根,然本題方程難以直接求解,為此又繼續轉化,將其轉化為函數的交點問題,最后利用數形結合的思路精準地求得了答案,這是解決此類問題的一個常用的方法,看來大家已經掌握了解題的精髓.生3結合題目特點,根據零點存在定理巧妙地解決了問題.

師:如果例1中需要求零點的個數,生3的方法還有效嗎?

通過交流,學生運用不同的解題方案順利地求解了問題,通過剖析發現解決此類問題可以從代數和幾何兩方面入手,同時體驗了數形結合思想和轉化思想在解題中的重要價值,為了進一步強化認識,教師又給出新問題,引導學生繼續探究,不斷挖掘,揭開問題的實質.

2.拓展應用,活躍思維

師:思考一下,下面問題該如何求解?

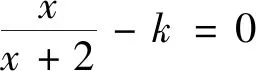
問題給出后,教師鼓勵學生從不同角度思考,進而通過拓展逐漸完善認知,鞏固應用.

生5:我沒有畫圖也做出來了,通分得(1-k)x-2k=0,所以當k=1時,無實數根,當k≠1時,方程有1個根.

師:生4和生5分別從幾何和代數的思路進行求解,他們的解題過程是否有問題呢?(眼尖的學生已經發現了問題)

生6:根據生5的代數式,是否要檢驗k一定不等于-2呢?

師:觀察得非常仔細,非常好!檢驗會發現k一定不等于-2.其實方程簡單的情況下用代數法更為方便,然在解題過程中一定要注意隱藏條件,要確保轉化的等價性.如果將例2中的函數做一些改變,你認為該如何求解呢?(教師PPT給出變式)

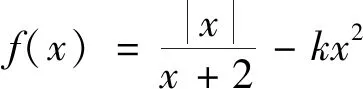
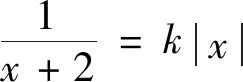
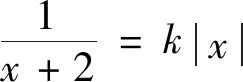
在教師的引導下,學生利用幾何方法輕松地解決了問題.問題解決后,教師又鼓勵學生利用代數法進行求解,然學生嘗試后發現,應用代數法問題變得更加復雜了,很難求解.通過對比學生發現,處理零點問題時可以應用代數法和幾何法,那么哪種方法為最優解決方案則需要根據實際問題來判斷,若是簡單的問題,利用代數法效率會更高,而對于較為復雜的問題,可以考慮借助圖形的直觀性來判斷,但是應用幾何法時,要使問題向容易作圖的方向轉化.

3.鞏固強化、升華認知

師:大家看看這個題又該如何轉化呢?(教師PPT展示變式2)

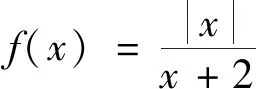
師:本題較前面問題相比,略顯復雜,是關于復合函數的零點問題,這個又該如何轉化呢?(教師鼓勵學生進行合作探究,以此既能活躍課堂氣氛,又能發揮個體優勢)

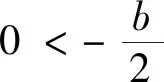
可見,通過以上的變式訓練,學生已經很好地掌握了解決此類問題的方法,極大程度上提高了解題信心.雖說高考題變化莫測,然若將知識點學懂吃透,規律會自然地涌現,新題變成了舊題,復雜題變成了簡單題,解題也就自然水到渠成了.

二、教學反思

在一輪復習中,以下幾點應引起師生重視:

首先,在解題教學中既要掌握通性通法,又要善于結合題型和題目特點進行靈活轉化.在夯實“雙基”的同時,也要積累一些解題技巧,提高解題效率.

其次,教師在典型問題的處理上要遵循由淺入深,從簡到繁的原則,使例子的呈現具備一定的層次性,順應學生思維發展,提高學生解題信心.

再次,對于一些規律性的問題,需要教師的及時點撥.對關鍵的方法和結論進行了及時的總結和歸納,引導學生認清問題的本質,找到解題通法.

最后,教師要為學生提供鞏固強化的時間和空間.教師應結合教學內容和學生認知設計變式題目,通過“變”感受通性通法的價值,體驗那些不變的規律,進而深化認知,活化數學思維,鍛煉學生靈活應用數學的能力.