教材尋法 巧解真題*
——以2023年高考圓錐曲線題為例

浙江省杭州學軍中學海創園學校 (311121) 陶勇勝

圓錐曲線問題是考查學生的數學運算和邏輯推理核心素養的重要抓手之一,在近幾年高考及各地模擬考試中,此類問題因在求解過程中含多個變量,往往具有較大且復雜的運算量,讓學生束手無策、望而生畏,是學生解題過程中的一個“痛”點.對于高考中的這一熱點和難點,如果能根據已知條件,選擇合適的直線參數方程,將會使得解題過程更為簡潔、高效.本文先介紹直線參數方程的相關概念,再以2023年圓錐曲線高考題為例,運用直線參數方程對其進行探究,回歸教材尋求突破之法.

1.直線參數方程的相關概念

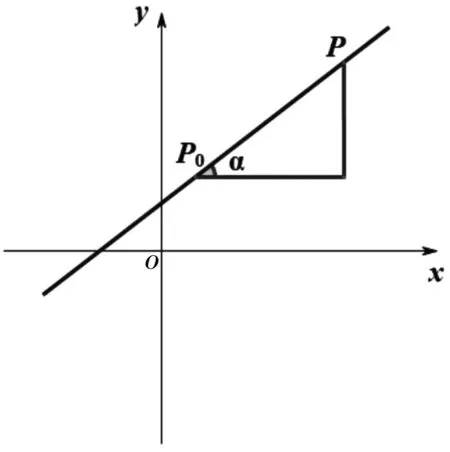
圖1

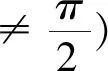
一般地,若過定點P0(x0,y0)直線l與二次曲線相交于P1、P2兩點,P1,P2對應參數分別為t1,t2,則根據參數方程中的t幾何意義,有以下性質:

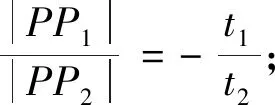
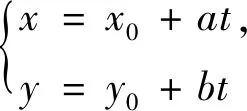
2.直線參數方程在圓錐曲線中的應用

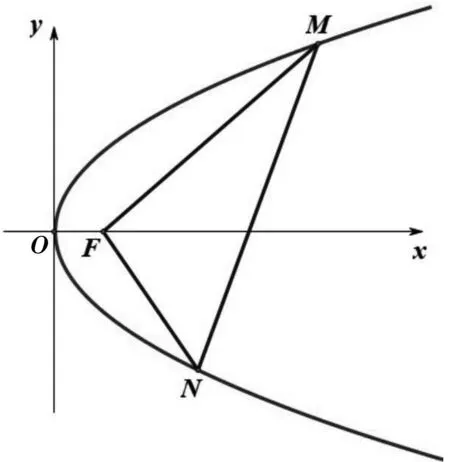
圖2

解:(1)易得p=2.

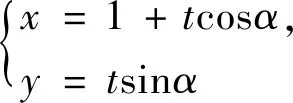
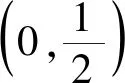
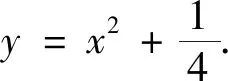
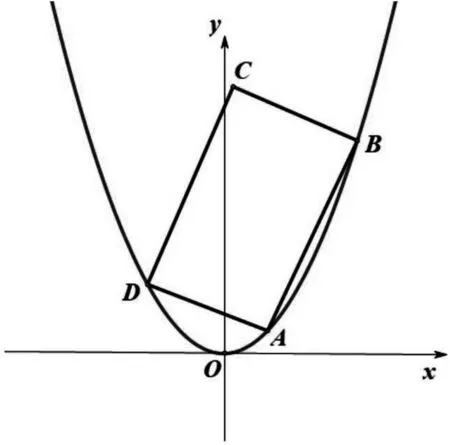
圖3

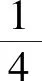
點評:該題設計巧妙、新穎,以一個邊長變化的矩形“搭”在拋物線上為載體,考查矩形在滑動過程中求矩形周長的最值問題,需要學生有一定的動態思維能力,又需要在變化過程中找到不變量的邏輯推理能力.本題選擇合適的直線參數方程,利用上述中的性質(1),簡潔地得到矩形兩邊的邊長,進而得到矩形周長L的表達式,突破本題的難點.由于(＊)式中各項均為正,周長L的最小值只有當分子為零時取得,整個解題過程簡潔、高效,避免了繁雜的運算.

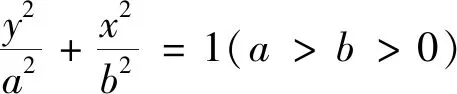
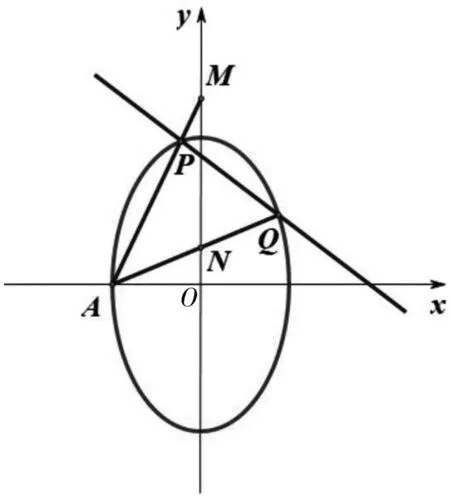
圖4

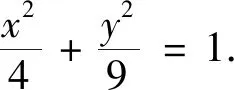
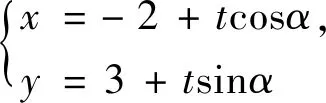
點評:該題以“若kAM+kAN為定值,則直線MN過定點”的定點問題為背景,其背景熟悉、表達簡練、切入口寬.本題的關鍵點是由直線AP、AQ的方程得到點M、N的坐標.設直線PQ的參數方程后,便捷得到點P、Q的坐標,再結合點A的坐標,得到直線AP、AQ的方程,突破本題的關鍵點.顯然,除了解決圓錐曲線中與長度有關的問題,直線的參數方程對于解決定點問題仍是一種十分高效的方法.實際上,此題與2022年全國數學理科乙卷第20題背景相似,也可以用直線的參數方程求解,讀者可以進行嘗試.

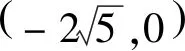
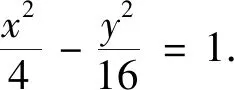
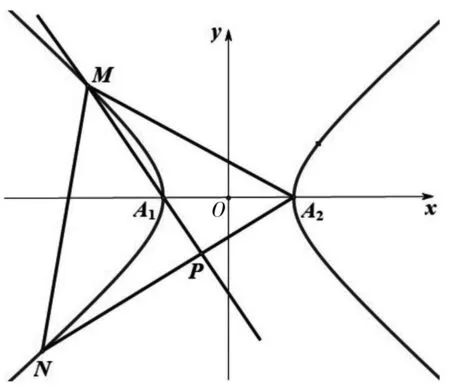
圖5

點評:該題考查直線與雙曲線的位置關系,可以從多個角度理解直線MN,點M、N可以看成直線MA1、NA2與雙曲線的交點,也可以看成直線MN與雙曲線的交點,即選擇直線MN的初始參變量不同,將導致解題過程的運算量大小不同.本題把點M、N看成直線MN與雙曲線的交點,巧設直線MN的參數方程,整個解題過程中始終將t作為初始參變量,大大減少了運算量.與例3相比,例4出現了非對稱韋達結構,常將sinα或cosα用t1、t2表示,轉化為關于t1、t2的一次式進行化簡運算,體現了轉化和化歸的數學思想.

3.教學啟示

3.1 深究教材,為教學活動多元化奠定基礎

直線的參數方程這一部分內容在新人教A版教材中以“探索與發現”的形式出現,似乎在高考中直接考查并不多,故在平時教學中容易忽視,但高三復習時,教師應充分挖掘新教材的思想,滲透新教材的方法,利用直線的參數方程開展多元化的教學活動,引導學生多題一解,拓寬學生的解題思路,在提高解題正確率的同時有助于學生擺脫解題慣性,培養學生的創新思維.

3.2 尋法教材,為破解高考真題提供良策

從近幾年圓錐曲線的高考試題來看,基于教材中的數學思想和方法為出發點的命制試題不在少數,教材是教師和學生學習知識的共同載體,也是高考命題的重要依據,命題專家根據教材挖掘有價值的材料,進行命題設計,能起到良好的導向作用,教師可與學生一起在教材中“尋法”,通過教材尋求破解方法,幫助學生實現“遷移數學知識、類比解題方法,從具體的教學情境中抽象出共性、方法和體系”[1],突破機械式“刷題”,使得“減負增效”落到實處.

3.3 回歸教材,為落實依標施教精準定位

章建躍博士認為:“回歸教材、依標施教是高考命題改革的大勢所趨,教材是從課標到教學的橋梁紐帶,教學中注重用好教材,切實做到依標施教”[2].如果教師脫離教材教學,一味追求教輔上的“二級結論”,熱衷“秒殺大招”,將導致學生在知識和方法遷移上捉襟見肘,遇到新的面孔,不能套路化,不會思考,長期以往,師生苦教苦學,教學效果甚微.唯有在課堂中注重教材中的通性通法,幫助學生在教師指導下,超越具體特技、特法深入到思維層面,注重學習的遷移運用和問題解決,在相似的情境中能夠做到“舉一反三”,才能使得學生真正成為學習的主人.

3.4 立足教材,為試題命制和解題教學把握方向

試題命制和解題教學都是教師在教學活動中不可缺少的重要技能,從教材中的數學思想和方法研究出發的試題命制和解題教學,既能幫助教師把握命題邏輯的正確性,確保命題試題的廣度和深度,也能幫助教師從不同角度對高考試題引申、類比和拓展,把高考試題價值最大化,還能幫助教師能從數學的本質出發,呈現知識的生成過程,使得復習備考真正做到“精準高效”.