一道2023年中國北方奧林匹克競賽試題的解法探究及其推廣

貴州師范大學數學科學學院 (550025) 文 帥 梁明端 袁興菊

1.試題呈現

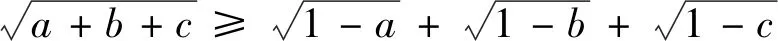
分析:這是2023年第十八屆中國北方奧林匹克競賽試題的一道不等式證明題,其中已知條件是以循環和的形式呈現,求證的不等式為根式的最值問題,形式上具有數學的美感.本文對該題進行解法探究,并對其進行變式和推廣,與大家一起分享.

2.解法探究

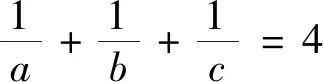
評注:此證法借助了柯西不等式.

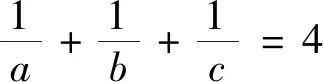
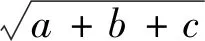
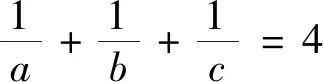
評注:此證法借助了基本不等式的推廣與柯西不等式.

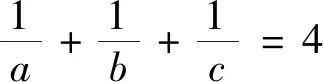
評注:此證法利用函數的凹凸性與琴生不等式,將不等式問題轉化為求函數最值問題.

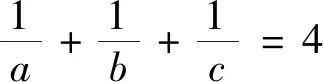
評注:此證法利用切線的性質,將不等式問題轉化為求函數最值問題.

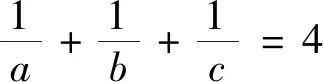
評注:此證法是從不等式本身進行分析,借助于均值不等式使問題得以證明.

3.試題變式

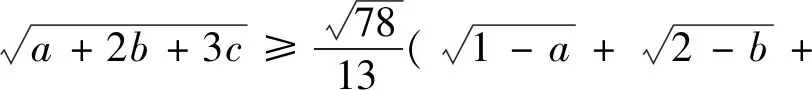
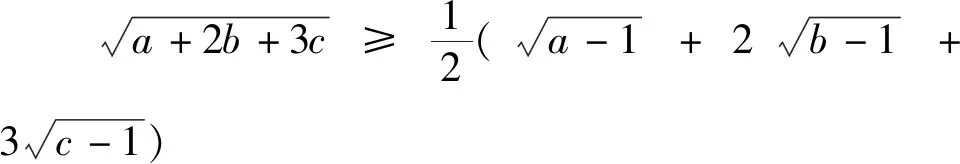
變式1與變式2在試題的基礎上改變不等式結構以及題設條件而得到的,證明方法與證法1類似,此處不再敘述.

4.試題推廣

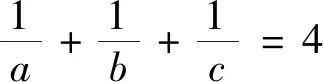
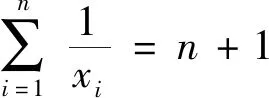
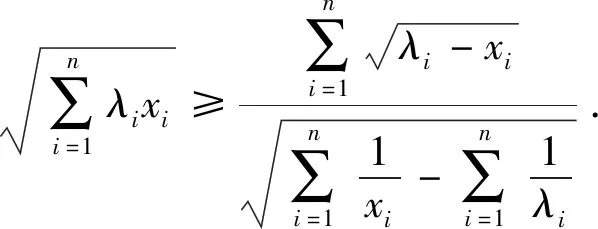
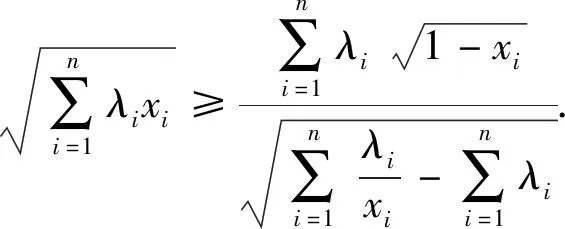
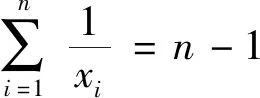
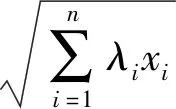
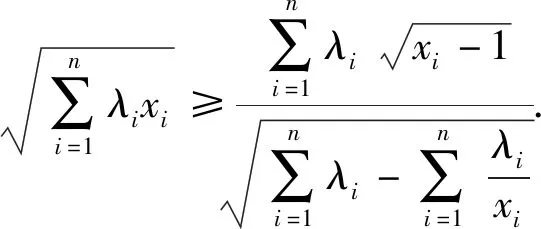
分析:上述推廣是在試題的基礎上改變不等式結構以及題設條件而得到的,下面列舉推廣3和推廣4的證明過程,其它推廣的證明過程不再敘述.

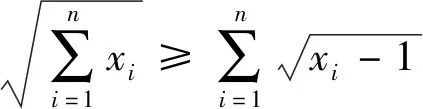
推廣,對于數學學習、數學競賽和數學研究有著十分重要的意義.在數學學習中,推廣可以加強觀察、分析、比較、綜合、概括、歸納、類比和發現的能力,拓展不同的解題思路,提升創造性的思維.在數學競賽中,推廣可以激發學習興趣與求知欲,引領新的發現[1]. 在數學研究中,推廣可以產生新問題與新方法,加深自身對問題的認識與理解[1].