基于APOS理論的初中數學概念教學的設計初探

張衡

【摘 要】? 為探究APOS理論的教學設計在數學教育中的應用，本文以"一次函數"單元為例，從行動、過程、對象、圖式四個階段的進行數學概念的教學設計，幫助提高初中學生對數學概念的理解和掌握程度.

【關鍵詞】? APOS理論；一次函數；數學概念；教學設計

數學教學一直以來都是一個需要不斷創新和改進的領域[1].隨著教育理論的不斷發展，越來越多的教學方法和原理被提出和運用到實際教學中.其中，APOS理論作為一種理論框架，為教學設計提供了新的思路和方法[2].APOS是指 Action，Process，Object，Schema（行動、過程、對象、圖式）四個階段，描述了學習數學概念的過程.本文以初中數學中的"一次函數"單元為例，探討了基于APOS理論的概念教學設計，旨在幫助學生深入理解和掌握一次函數的概念、性質和應用.

1? “一次函數”概念的教學設計

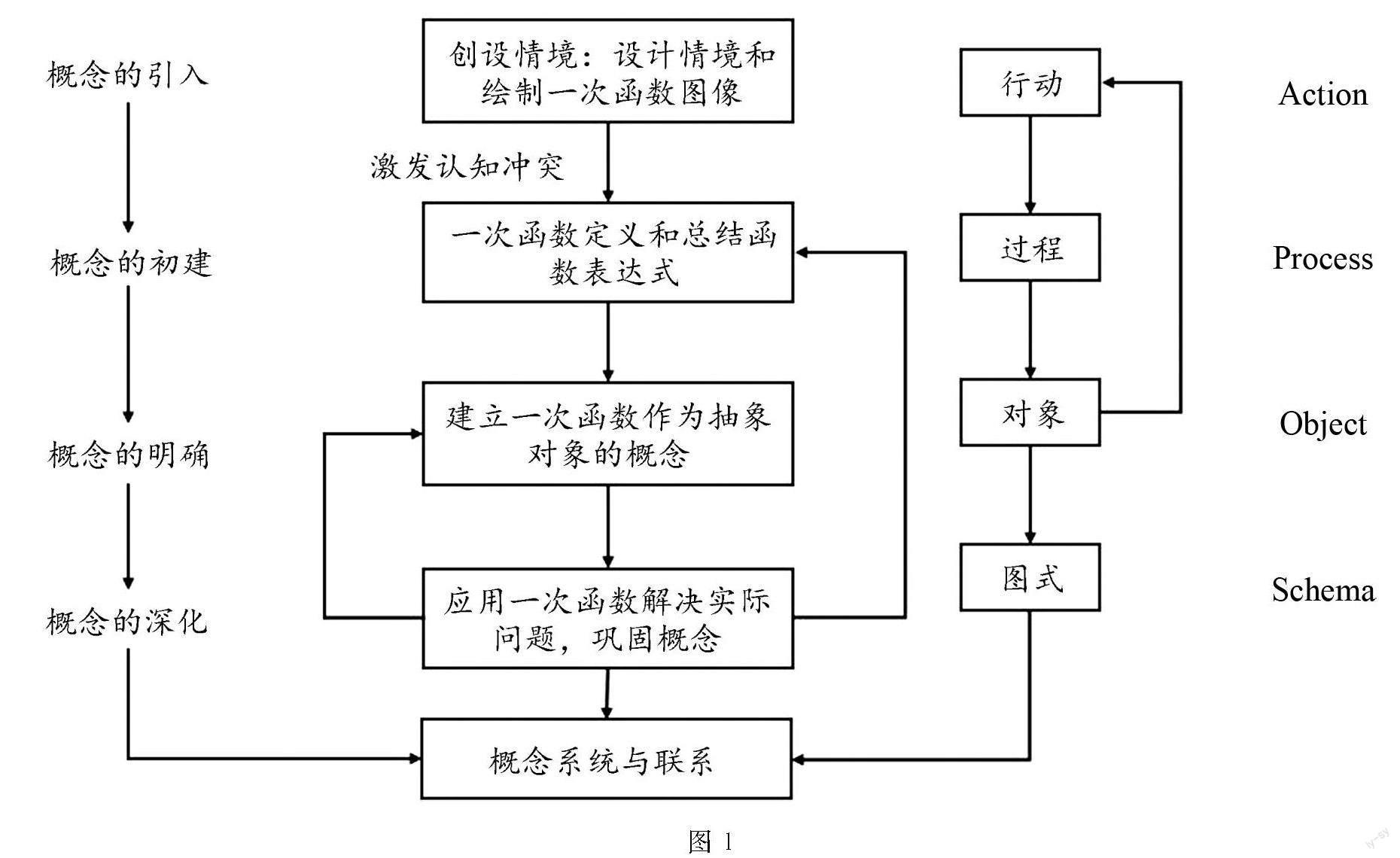
基于APOS理論對該單元進行概念教學設計的探究流程如下圖1所示.

圖1

2.1? 行動階段-創設情境感知概念

在第一個階段可以通過引導學生通過直觀的操作和實際的例子，感知一次函數的特征和性質，引發學生對一次函數的興趣和思考.

情境引入? 如圖2，如果我們知道一個物體A從一個位置出發，以一定的速度勻速向右運動，我們能否根據時間來確定物體的位置呢？

圖2

教師：在上述情境中，哪個量是固定不變的？哪個量是變化的？

學生1：因為是勻速行動，則速度是不變的.

學生2：變量是時間，時間在變化.

教師：行駛的距離和時間構建函數為，當這里的速度=80m/min，你能求出=10min，t2=20min時物體運動的距離嗎？請分別列出他們的表達式.

學生3：S1=·=8010=800m，S2=·=8020=1600m.

教師：引入一次函數的概念，一次函數表示了兩個變量之間的線性關系.其中，t是自變量，s是因變量.當t增加或減少時，s的值也按照一定的比例增加或減少.

實際操作? 將學生分為幾個小組，讓他們按照圖3將木板墊起來至不同高度，觀察小球的運動速度，小球到達底端的時間.

圖3

學生4：模板越高越斜，小球運動得越快，到達木板底部的距離越短.

教師：一次函數的代數表示形式是y=mx+b，其中m是斜率，b是截距.通過這個實驗我們可以知道斜坡傾斜程度和小球下滑速度之間的關系，可以很好的理解斜率這個特性.那么對于截距該如何理解？

學生5：表示當自變量為0的時候，起始的情況.

教師：設計一個人走的距離實驗.學生可以使用不同的起始位置開始行走，并測量記錄每個位置對應的步數和距離.教師：展示一次函數圖像如圖4.讓學生思考一次函數圖像特性以及一次函數的基本概念.

圖4

設計意圖：通過直觀的操作和實際的例子，學生可以更好地感知一次函數的特征和性質，從而對其有更深刻的理解.

2.2? 過程階段-解決問題初建概念

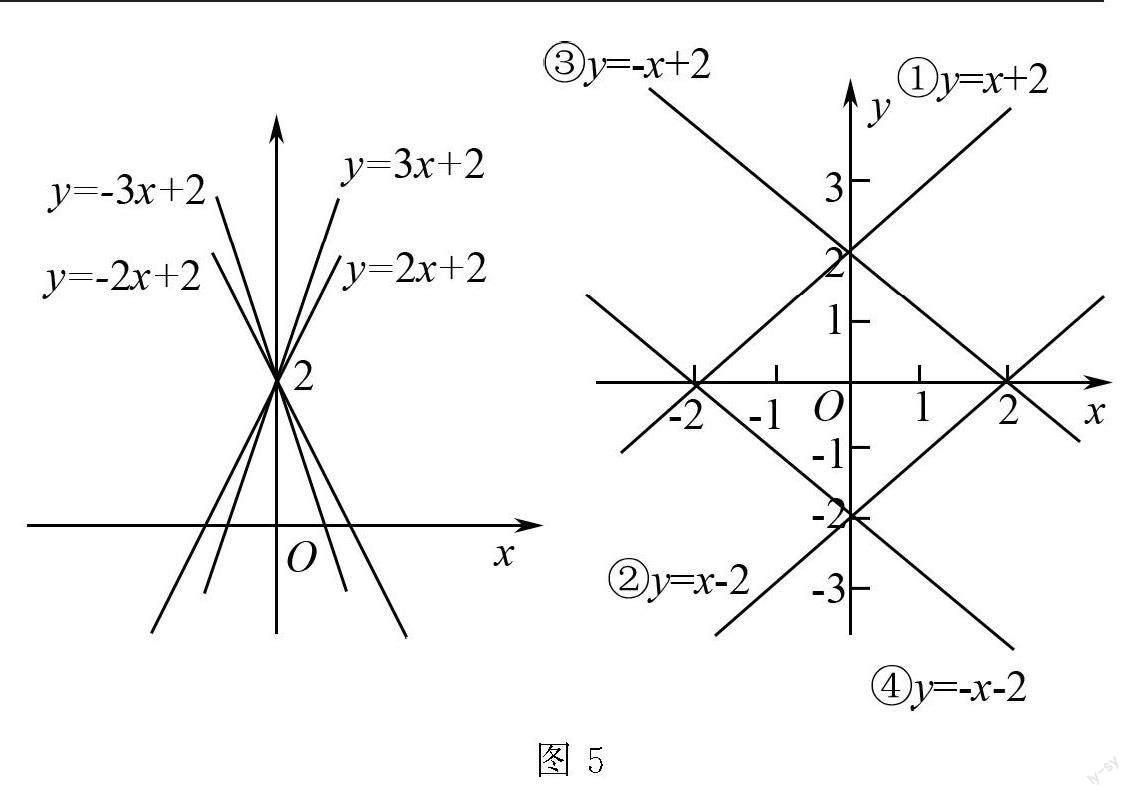
探究過程? 教師向學生展示不同斜率和截距的直線函數如圖5.

圖5

教師：對圖像對應的直線進行講解，讓學生觀察和分析一次函數的圖像特征，引導他們發現斜率、截距和圖像形狀之間的關系.

學生6：斜率表示直線的傾斜程度或者斜率的大小.

學生7：當斜率為正數時，直線向上傾斜.這表示隨著自變量x的增加，因變量y的值也會增加.斜率越大，變化越陡峭.

學生8：當斜率為負數時，直線向下傾斜.這表示隨著自變量x的增加，因變量y的值會減少.斜率越小（即絕對值越大），變化越陡峭.

教師：斜率和截距是直線性質中重要的參數，它們決定了直線的斜率、傾斜方向、位置和平移.

解決問題? 瑪麗買了一些蘋果，她每天吃掉的蘋果數量和剩余的蘋果數量之間存在一種線性關系.已知第一天剩下10個蘋果，經過5天后，剩下2個蘋果.利用一次函數來解決經過6天后，預計還剩下幾個蘋果？

學生9：假設函數的自變量為天數（x），因變量為剩余蘋果數量（y）.通過題意可以得到兩對坐標點：（1，10）和（5，2），得一次函數為

學生10：將x=6，代入一次函數中，y=0，則預計剩下0個蘋果.

教師：根據這個實例，學生將一次函數運用其中，對一次函數的概念、性質以及應用更加理解.

3? 反思感悟

在這個教學設計中，需要注重設計了各種互動和探究活動，通過讓學生積極參與掌握知識，可以激發他們的興趣和動力.并強調將新的數學概念與學生已有的知識和經驗進行連接，可以幫助學生更容易地理解和接受新的概念.使用圖表、方程、實例等來表達和解決一次函數的問題學生靈活地在不同的表征形式中轉換和應用知識，可以促進他們對概念的深入理解.

參考文獻：

[1]彭小烜.基于APOS理論的初中數學概念教學優質課的特征研究[D].重慶三峽學院，2023.

[2]王悅，馬旭.APOS理論指導下的初中數學概念課教學——以“直線、射線和線段”為例[J].數學教學通訊，2023（14）：10-13.