杠桿平衡條件的三類典型應用
李鑒秀


【摘要】本文通過對獨輪車、桿秤和塔吊等具體案例進行分析,闡述杠桿平衡條件的應用方法,旨在提供對杠桿平衡條件的深入理解,并展示其在不同領域的廣泛應用.
【關鍵詞】杠桿平衡條件;初中物理;解題技巧
杠桿平衡條件是物理學中的一個基本原理,它描述了杠桿在平衡狀態下的力和力矩之間的關系.這個原理在多個領域中都有廣泛的應用,本文將探討杠桿平衡條件的幾類典型應用,并通過具體案例進行分析.
1? 杠桿的平衡原理概述
在物理學中,杠桿的力臂是指從杠桿的支點到力作用線的垂直距離.根據杠桿平衡條件,當力臂與力的乘積相等時,杠桿處于平衡狀態.掌握這個概念在解決與杠桿相關的問題時非常重要.
2? 杠桿平衡條件的典型應用
2.1? 獨輪車的平衡
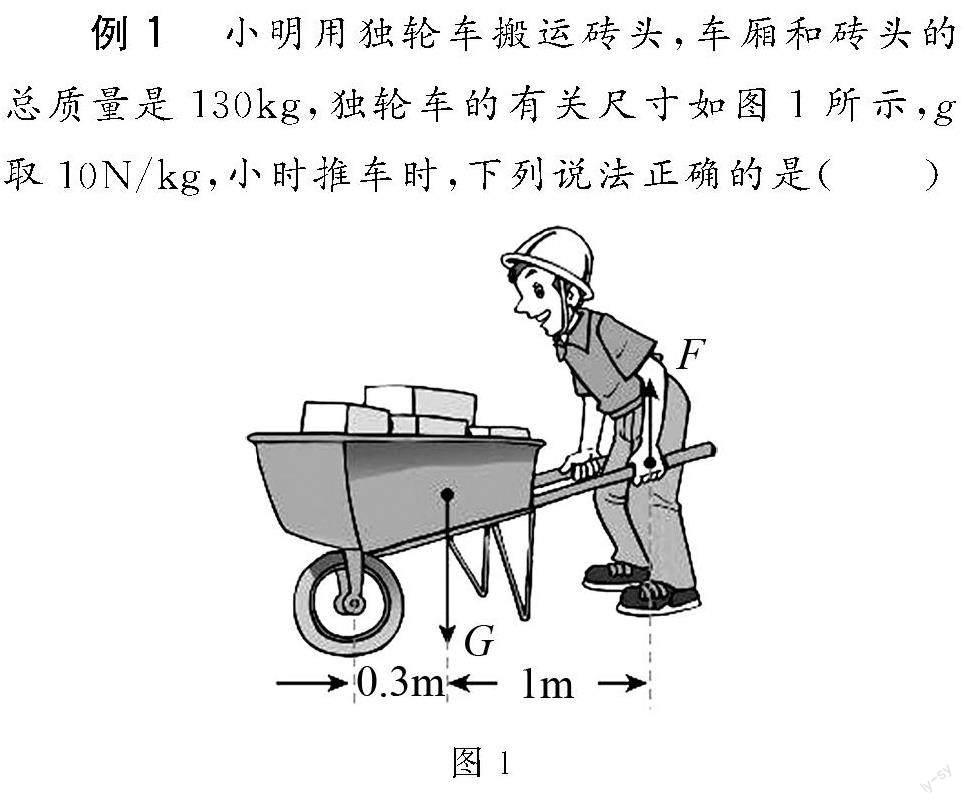
例1? 小明用獨輪車搬運磚頭,車廂和磚頭的總質量是130kg,獨輪車的有關尺寸如圖1所示,g取10N/kg,小時推車時,下列說法正確的是(? )
(A)獨輪車是費力杠桿.
(B)動力臂是0.7m.
(C)阻力臂是1m.
(D)人手豎直向上的力F的大小是300N.
解析? 由圖1可知,獨輪車在使用過程中,動力臂大于阻力臂,是省力杠桿,故(A)錯誤;支點在車輪的軸上,力F為動力,所以動力臂的長度為1.3m,阻力是G,阻力臂的長度為0.3m,故(B)(C)錯誤;磚頭及車廂的總重G=mg=130kg×10N/kg=1300N,由杠桿平衡條件F1l1=F2l2可知,人手豎直向上的力F=Gl2l1=1300N×0.3m1.0m+0.3m=300N,故(D)正確.
點評? 獨輪車的平衡是一種典型的杠桿平衡問題,它利用杠桿平衡原理,并讓動力臂大于阻力臂達到省力的作用.
2.2? 桿秤的原理
例2? 桿秤是我國古代勞動人民的一項發明,是各種衡器中歷史最悠久的一種,稱量物體質量時,它相當于一個杠桿.某桿秤的示意圖如圖2所示,C處是秤鉤,A,B位置各有一個提紐,桿秤秤桿(包含秤鉤、提紐)的重力為1N,秤砣質量為0.5kg,BC=7cm.提起B處提紐,秤鉤不掛物體,將秤砣移至D點,桿秤恰好水平平衡,BD=1cm,則桿秤秤桿(包含秤鉤、提紐)的重心O點到B點的距離為??? cm;將質量為2.5kg的物體掛在秤鉤上,提起B處提紐,將秤砣移至最大刻度E處,當桿秤再次水平平衡時BE=??? cm.若要稱量質量更大的物體,應選用??? 提紐(選填“A”或“B”).
解析? 秤鉤不掛物體時,由杠桿的平衡條件可知G砣×BD=G秤×LOB,根據G=mg,可得m砣g×BD=G秤×LOB,所以桿秤秤桿的重心O點到B點的距離為LOB=m砣g×BDG=5cm;將質量為2.5kg的物體掛在秤鉤上時,由杠桿平衡條件可知:G物×BC=G秤×LOB+G砣×BE,代入數據解得BE=34cm;根據杠桿的平衡條件,提著B處秤紐、秤砣在E點時,G物×BC=G秤×L0+G砣×BE,提著A處秤紐、秤砣在E點時,G物′×AC=G秤×(L0+AB)+G砣×(BE+AB),因BC>AC,故可得G物′>G物,即提A處秤紐時,此秤的稱量大.
點評? 桿秤是一種利用杠桿平衡條件來測量物體質量的儀器.桿秤的兩端分別放置待測物體和秤砣,通過調整秤砣端的力臂,使杠桿達到平衡狀態.根據杠桿平衡條件,當兩端的力矩相等時測量待測物體的質量.
2.3? 塔吊的工作原理
例3? 西安幸福林帶工程是全球最大的地下空間利用工程之一(如圖3).一派繁忙施工景象,建設工地上的“塔吊”打算吊起底面積為0.8m2,質量為2400kg的圓柱形重物,A為塔吊的配重,OB是長為25m的起重臂,C為能在起重臂上移動的載重小車,載重的小車下面掛有滑輪組,當小車滑到B點時,“塔吊”能安全吊起最大質量為1200kg的重物.現小車從距離O點為10m的載重臂上打算吊起該圓柱形重物,掛鉤、滑輪組和鋼絲繩的質量不計,g取10N/kg.則:
(1)起吊前,重物對地面的壓強為多大?
(2)起吊后,當重物勻速上升時每段鋼絲繩的拉力為多大?
(3)若將該圓柱形重物勻速提升20m,則拉力做功多少?
(4)塔吊將重物從起吊點提升20m后,載重小車最多能向B點方向再平移多少米才能保證安全工作?
解析? (1)重物的重力G=mg=2400kg×10N/kg=24000N,起吊前,重物對地面的壓力等于自身重力,對地面的壓強p=FS=GS=24000N0.8m2=3×104Pa.
(2)由圖3可知,承重重物的鋼絲繩有4根,在不計掛鉤、滑輪組和鋼絲繩重及摩擦時,每段鋼絲繩的拉力F=14G=14×24000N=6000N.
(3)重物提升20m,繩子自由端移動的距離s=4h=4×20m=80m,拉力做的功W=Fs=6000N×80m=4.8×105J.
(4)載重小車在B點時,能吊起重物的最大質量為1200kg,據杠桿平衡條件有G配重×OA=1200kg×10N/kg×25m,將重物向B移動過程中,配重及對應的力臂不變,據杠桿平衡條件有24000N×L=1200kg×10N/kg×25m,解得L=12.5m.所以載重小車最多通向B點移動的距離L1=L-l=12.5m-10m=2.5m.
點評? 塔吊利用杠桿平衡條件來提升和搬運重物.它通過將杠桿系統與電動驅動相結合,實現對重物的起重和移動,杠桿的長度和位置的設計是關鍵,以確保起重過程的穩定性和安全性.
3? 結語
通過上述的典型案例分析,讓學生認識杠桿平衡條件在日常生活和機械工程中都有廣泛的應用.理解和應用杠桿平衡條件可以幫助學生更好地理解和解決與力和力矩相關的問題,同時也為設計和操作各種機械設備提供了理論基礎.在實際應用中,合理利用杠桿平衡條件可以實現省力、提高效率和操作的便利性.
參考文獻:
[1]王偉民,辛存良.運用杠桿平衡條件,確定剩余部分重心[J].物理教師,2018,39(07):91-92.
[2]魏喜武.拓展杠桿平衡條件在解題中的應用[J].物理教學探討,2012,30(07):46-47.

