考慮通信拓撲切換的多導彈協(xié)同制導研究

張世強 李群生 何金剛

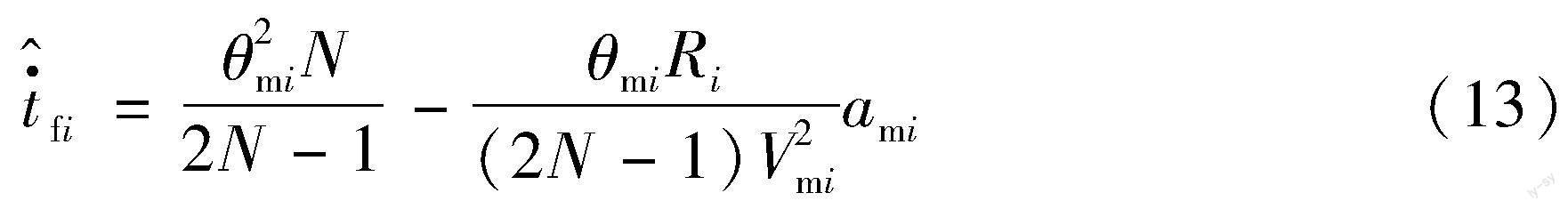
摘 要：????? 針對通信拓撲切換下多導彈協(xié)同打擊問題， 提出了一種基于切換策略的時空協(xié)同制導律。 針對時間約束， 結(jié)合一致性算法設計分布式制導律， 并基于李雅普諾夫理論證明系統(tǒng)在有限時間收斂， 可以實現(xiàn)同時打擊。 對于空間約束， 采用彈道成型制導律使各導彈收斂到期望的視線角。 設計切換策略， 使得導彈能夠同時實現(xiàn)時間和角度協(xié)同攻擊。 仿真分析驗證了所設計制導律能在切換拓撲條件下和彈群失去1枚導彈的情況下實現(xiàn)齊射攻擊和角度約束。

關(guān)鍵詞：???? 協(xié)同制導； 切換拓撲； 時間約束； 角度約束； 制導律； 速度不可控

中圖分類號：??? ???TJ765； V249

文獻標識碼：??? A

文章編號：??? ?1673-5048（2024）01-0038-07

DOI： 10.12132/ISSN.1673-5048.2023.0099

0 引? 言

隨著各種軍事新技術(shù)不斷出現(xiàn)， 導彈與目標的攻防越來越復雜。 無論是“近防炮”和“定向能激光武器”， 還是各種干擾設備的出現(xiàn)， 都對導彈的發(fā)展提出了越來越高的要求。 因此， 建立多導彈協(xié)同攻擊體系， 實現(xiàn)多導彈協(xié)同攻擊， 是應對未來戰(zhàn)爭的重要技術(shù)手段， 可以有效提升導彈在強對抗環(huán)境下的快速突防和目標毀傷能力。

現(xiàn)有文獻中， 針對協(xié)同制導的研究主要從時間約束和角度約束出發(fā)。 其中時間約束是協(xié)同制導律的前提， 主要是滿足多導彈齊射攻擊的要求。 時間協(xié)同制導律有指定攻擊時間的協(xié)同制導律， 這種制導律的各導彈之間沒有通信交流。 文獻［1］將比例導引法與最優(yōu)控制結(jié)合， 設計了一種比例導引法加時間偏置項的協(xié)同制導律。 文獻［2］根據(jù)非線性方程， 提出一種具有更嚴格形式的協(xié)同時間制導律。 文獻［3］針對指定攻擊時間和非線性模型， 提出一種基于滑膜控制的時間協(xié)同制導律， 避免了奇異現(xiàn)象。 但是， 戰(zhàn)場情況瞬息萬變， 很難選擇合理的攻擊時間， 而一旦攻擊時間的選擇不合適， 整個多導彈制導系統(tǒng)就很難收斂， 從而無法實現(xiàn)協(xié)同攻擊。 多導彈之間通過信息交流實現(xiàn)協(xié)同攻擊是解決指定攻擊時間選擇困難的有效途徑。 文獻［4］提出一種領(lǐng)從式的時間協(xié)同制導律， 并且推廣到速度不同的情況。 文獻［5］同樣基于領(lǐng)從式架構(gòu)設計協(xié)同制導律， 其中領(lǐng)彈和從彈分別設計滑模制導律， 可以對非機動目標實現(xiàn)協(xié)同打擊。 文獻［6］提出一種以比例導引法為基礎， 導航比時變的協(xié)同制導律， 通過減少多導彈剩余時間之間的一致性誤差， 達到齊射攻擊。 文獻［7］結(jié)合非線性滑模控制和一致性理論， 提出一種非奇異的協(xié)同制導律， 可以實現(xiàn)在大前置角初始條件下， 多導彈協(xié)同攻擊地面靜止目標。 角度約束是指導彈以一定的空間構(gòu)型命中目標， 能有效對抗高防護目標， 提高對高價值目標的毀傷效果。 文獻［8］提出一種落角約束的偏置比例導引律， 通過時變增益調(diào)節(jié)各導彈的剩余飛行時間， 通過偏置項控制落角。 文獻［9-11］結(jié)合多智能體一致性和滑模控制理論， 將制導律的設計分為視線法向和視線切向， 實現(xiàn)導彈對目標的時空約束打擊。 但要求導彈全程軸向速度可控， 實際應用難度較大。

現(xiàn)有關(guān)于協(xié)同制導的研究中， 均是假設各飛行器之間的通信處于理想條件下， 通信拓撲固定。 在實際作戰(zhàn)中， 由于部分導彈被擊落、 通信設備限制、 障礙物遮擋和電磁干擾等影響， 導彈之間的通信不是固定的， 彈群的通信拓撲可能會切換， 這種情況不僅會降低多導彈系統(tǒng)的協(xié)同性能， 甚至破壞協(xié)同的效果， 造成整個制導系統(tǒng)發(fā)散。 因此， 需要所設計的時間協(xié)同制導律對切換通信拓撲具有一定的容錯能力。 文獻［12-13］提出一種分布式切換拓撲的協(xié)同制導律， 可以實現(xiàn)對目標的齊射攻擊，? 但沒有實現(xiàn)角度協(xié)同。 文獻［14］采用一階多智能體一致性理論， 針對通信拓撲切換的情況設計了一種協(xié)同制導律， 可以實現(xiàn)時間的協(xié)同。

綜上所述， 現(xiàn)有的多導彈協(xié)同制導律設計大多數(shù)基于通信實時交流的假設， 并且在面對通信拓撲切換的制導律設計中， 所關(guān)注的主要是時間約束問題， 缺少空間中的協(xié)同， 因此， 實現(xiàn)速度不可控導彈時間和空間的協(xié)同仍是需要解決的問題。 本文提出了一種切換的時空協(xié)同制導律， 在通信拓撲切換的情況下， 各導彈的剩余飛行時間收斂一致， 并且末端視線角收斂到各自的期望值。

1 問題描述

1.1 協(xié)同攻擊模型

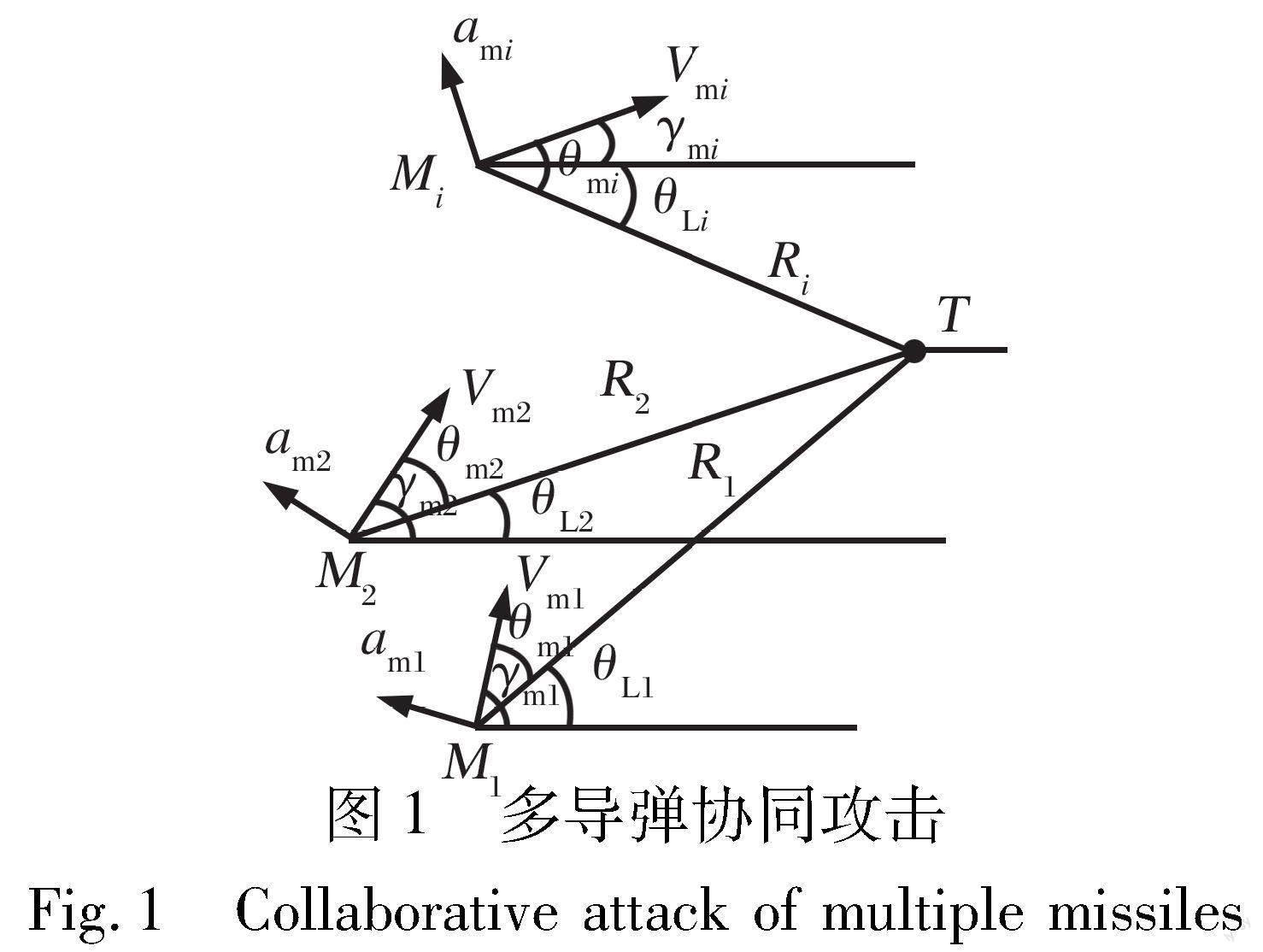
考慮平面攻擊場景， 相對幾何關(guān)系如圖1所示。 假設導彈的導引頭和自動駕駛環(huán)節(jié)時間常數(shù)小， 可以忽略不計， 導彈的速度大小不變。

圖中， T和Mi分別表示目標和第i枚導彈； Ri為目標和導彈之間的相對距離； Vmi為導彈的速度； γmi為目標和導彈的彈道傾角， θmi為導彈的前置角， θLi為視線角。 則制導模型的運動學方程如下：

1.2 圖? 論

目前導彈間的通信拓撲一般使用圖論來描述， 本文多導彈之間使用無向圖G（υ， ζ， A）描述。 其中， υ表示節(jié)點集合， ζ表示邊的集合， A=［aij］表示臨接矩陣。 若圖G是無向圖， 則aij=aji。 定義圖G的拉普拉斯矩陣為L=［lij］N×N， 假如導彈之間可以相互傳遞信息， 則aij>0， 反之a(chǎn)ij=0。 其中：

引理1［15］： 若x1， x2， …， xn≥0且0<μ<1， 則如下不等式成立：

引理2［16］： 如果圖G是無向且連通的， 則對任意ξ=［ξ1，ξ2，…，ξn］T∈Rn且滿足1Tξ=0， 都有ξTLξ≥λ2（L）ξTξ， 其中， 1=［1， 1， …， 1］T。

引理3［17］： 如果圖G是無向且連通的， λ2（L）是L的第二小的特征值， 則有λ2（L）>0。

式中： β和p是正常數(shù)， 且p∈（0， 1）， 則可知系統(tǒng)狀態(tài)能在有限時間內(nèi)收斂到平衡點且收斂時間滿足

1.3 設計目標

為了實現(xiàn)多導彈在通信拓撲切換情況下的時空協(xié)同， 應該使各導彈之間的剩余飛行時間趨于一致， 但剩余飛行時間很難得到， 所以選擇預測剩余飛行時間t^goi作

為協(xié)調(diào)變量， 因此協(xié)同制導律的目標為

式中： θfi為期望的視線角。

2 多導彈協(xié)同制導律設計

2.1 時間制導律設計

本節(jié)的設計目標是在導彈通信無向且切換的條件下使所有導彈的剩余飛行時間收斂到一致。

定義導彈預測飛行時間為［6］

設預測攻擊時間為

假設每枚導彈的視場角絕對值為小量， 則可以得到如下近似：

對式（11）求導并將式（12）帶入可得協(xié)同制導模型：

受文獻［12-14］的啟發(fā)， 設計如下制導律：

式中： 0<α<1； sig（x）α=sgn（x）xα。 只要當通信拓撲無向， 并且整個制導過程的總連通時間大于Tc， 則式（14）的制導律可以使多導彈的剩余時間在有限時間內(nèi)收斂：

證明： 將式（14）代入式（13）可得

因為通信拓撲始終是無向的， 則有

由式（17）可得

令

其中：

由式（18）～（20）可得

由式（16）可得

選擇Lyapunov函數(shù)如下：

對式（24）求導， 并將式（22）～（23）代入可得

由式（25）可知系統(tǒng)漸進穩(wěn)定。 當系統(tǒng)通信拓撲在某個時間段處于固定且聯(lián)通的狀態(tài)：

由引理1可知：

設B=［a2/（1+α）ij］∈Rn×n， δ（t）=［δ1（t）， δ2（t）， …， δn（t）］，

由式（22）可得

1Tδ=0（28）

由引理2可得

由引理2和引理3可得

式中： L（B）為圖G（B）的拉普拉斯矩陣； λ2［L（B）］為第二小的特征值。

在系統(tǒng)通信拓撲無向且連通下所對應的整個時間區(qū)間內(nèi)， 令K1=λ2［L（B）］>0， 則

由引理4可得

其中：

由式（33）和式（19）可得

集合式（35）和式（11）， 在通信無向且連通并且總聯(lián)通時間大于T1時， 多導彈的剩余飛行時間趨于一致：

當彈群因為電磁干擾或其中1枚導彈被擊落導致彈群通信拓撲變換時， 由式（24）～（25）可知系統(tǒng)全局漸進穩(wěn)定， 此時的彈群制導系統(tǒng)仍可以保持穩(wěn)定。 對于新組成的通信拓撲， 只要制導律（14）滿足要求， 則仍然可以同時命中目標， 實現(xiàn)協(xié)同打擊。

2.2 時間角度協(xié)同制導律

為了增加毀傷效果和突防能力， 提高對隱身目標的探測能力， 在導彈同時攻擊目標的基礎上設計角度制導律， 使多導彈同時收斂到期望的視線角。 角度控制制導律可以選用彈道成型制導律［19］， 導彈成型制導律不受導彈通信的影響：

式中： θLfi為期望視線角。

算法流程如圖2所示。

綜上， 整體制導律設計為： 估算各導彈的剩余飛行時間， 并計算剩余飛行時間之差， 當最大剩余飛行之差大于允許誤差時， 制導律切換為時間制導律， 當滿足時間約束后， 制導律切換為角度制導律：

其中： ε1， ε2為允許誤差； emax為最大剩余飛行時間之差。 定義sgn1（x）=1， x<0； sgn1（x）=0， x>0； sgn2（x）=0， x<0； sgn2（x）=1， x>0。 當最大剩余飛行之差大于ε1， 采用時間協(xié)同制導律； 當最大剩余飛行之差小于ε2， 采用角度制導律； 當最大剩余飛行之差在ε1和ε2之間時， 制導律保持不變； ε1和ε2的滯后減少了制導律的震蕩。

3 仿真驗證

對所設計的時空協(xié)同制導律進行仿真驗證。 設置仿真場景為4枚導彈在滿足空間約束的情況下協(xié)同攔截1個固定目標， 仿真參數(shù)和指標設置如表1所示， 通信拓撲回路如圖3所示， 其中每2 s拓撲切換一次， 為了更符合實際情況， 限制導彈法向過載30g， 導彈視場角假設為前置角。 在切換拓撲圖3的情況下， 方法A采用本文所設計的制導律式（38）， 制導參數(shù)選擇N=3.5， α=0.64， ε1=1， ε2=0.6。 方法B采用文獻［14］提出的制導律， 參數(shù)選擇N=3， α=0.6。

每個拓撲結(jié)構(gòu)所對應的臨接矩陣為

仿真結(jié)果如圖4～10所示。 其中， 脫靶量和制導時間如表2所示。

由圖4～10和表2可知， 在切換拓撲情況下， 兩種制導律都能使4枚導彈成功命中目標。 由圖8和表2可知， 方法A的各導彈的剩余時間誤差在0.5 s以內(nèi)， 最大脫靶量2.27 m， 方法B的剩余時間誤差0.1 s， 最大脫靶量2.49 m， 兩者性能接近。 但由圖5可知， 與方法B相比， 方法A的導彈過載除了最開始1 s內(nèi)的震蕩， 其余時間相對平緩。 由圖9～10可知， 兩種方法下導引頭視場角都在絕對值40°內(nèi)變化， 但方法A的視場角速度平緩， 可以提高導彈的打擊精度。 由圖6可知， 方法A的導彈視線角都收斂到期望值， 且視線角誤差在0.1°以內(nèi)， 從而驗證了所設計二維時空約束協(xié)同制導律的有效性。

設其中1枚導彈中途被擊落， 通信拓撲變化如圖11所示。 1枚導彈被擊落的時間設置為18 s， 制導參數(shù)選擇N=3.5， α=0.58， ε1=1， ε2=0.6， 導彈初始條件不變。

每個拓撲結(jié)構(gòu)所對應的臨接矩陣為

仿真結(jié)果如表3和圖12～18所示。

由表3和圖12～18可知， 在1枚導彈被擊落的情況下， 剩余的3枚導彈仍然實現(xiàn)了協(xié)同打擊， 攻擊時間誤差在0.5 s， 并且導彈的視線角也收斂到了期望值， 最大脫靶量也不超過2.2 m， 說明制導律具有很強的魯棒性。

4 結(jié)? 論

本文針對在切換拓撲下的多導彈協(xié)同攻擊問題， 提出了一種切換策略的時空協(xié)同制導律， 并且將時間制導律和空間制導律結(jié)合， 解決了現(xiàn)有對切換拓撲下制導律的研究只專注于時間協(xié)同的問題， 實現(xiàn)了角度協(xié)同。? 由

仿真結(jié)果可得， 相對于現(xiàn)有文獻， 本文所設計的制導律在通信拓撲切換的情況下， 脫靶量和剩余時間誤差性能相同， 最大脫靶量不超過2.3 m， 最大時間誤差在0.5 s以內(nèi)， 并且切換制導律的終端視線角收斂到期望角度， 誤差不超過0.1°， 各導彈的視線角速度和法向過載更加穩(wěn)定， 有利于導彈的協(xié)同探測和突防。

參考文獻：

［1］ Jeon I S， Lee J I， Tahk M J. Impact-Time-Control Guidance Law for Anti-Ship Missiles［J］. IEEE Transactions on Control Systems Technology， 2006， 14（2）： 260-266.

［2］ Jeon I S， Lee J I， Tahk M J. Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation［J］. Journal of Guidance， Control， and Dynamics， 2016， 39（8）： 1887-1892.

［3］ Cho D， Kim H J， Tahk M J. Nonsingular Sliding Mode Guidance for Impact Time Control［J］. Journal of Guidance， Control， and Dynamics， 2016， 39（1）： 61-68.

［4］ 張友安， 馬國欣， 王興平. 多導彈時間協(xié)同制導： 一種領(lǐng)彈-被領(lǐng)彈策略［J］. 航空學報， 2009， 30（6）： 1109-1118.

Zhang Youan， Ma Guoxin， Wang Xingping. Time-Cooperative Guidance for Multi-Missiles： A Leader-Follower Strategy［J］. Acta Aeronautica et Astronautica Sinica， 2009， 30（6）： 1109-1118.（in Chinese）

［5］ 趙斌， 黃曉陽， 周軍， 等. 基于滑模控制的多彈分布式視線協(xié)同制導律設計［J］. 空天防御， 2020， 3（3）： 16-23.

Zhao Bin， Huang Xiaoyang， Zhou Jun， et al. Multi-Missile Distri-buted LOS Cooperative Guidance Law Design Based on Sliding Mode Control［J］. Air & Space Defense， 2020， 3（3）： 16-23.（in Chinese）

［6］ Jeon I S， Lee J I， Tahk M J. Homing Guidance Law for Cooperative Attack of Multiple Missiles［J］. Journal of Guidance， Control， and Dynamics， 2010， 33（1）： 275-280.

［7］ 楊小艷， 張金鵬， 馬慧敏， 等. 多彈分布式時間協(xié)同非奇異制導方法［J］. 航空兵器， 2022， 29（1）： 35-40.

Yang Xiaoyan， Zhang Jinpeng， Ma Huimin， et al. Nonsingular Distributed Guidance Method for Time-Coordinated Attack with Multiple Missiles［J］. Aero Weaponry， 2022， 29（1）： 35-40.（in Chinese）

［8］ 張春妍， 宋建梅， 侯博， 等. 帶落角和時間約束的網(wǎng)絡化導彈協(xié)同制導律［J］. 兵工學報， 2016， 37（3）： 431-438.

Zhang Chunyan， Song Jianmei， Hou Bo， et al. Cooperative Gui-dance Law with Impact Angle and Impact Time Constraints for Networked Missiles［J］. Acta Armamentarii， 2016， 37（3）： 431-438.（in Chinese）

［9］ 呂騰， 呂躍勇， 李傳江， 等. 帶空間協(xié)同的多導彈時間協(xié)同制導律［J］. 航空學報， 2018， 39（10）： 322115.

Lü Teng， Lü Yueyong， Li Chuanjiang， et al. Time-Cooperative Guidance Law for Multiple Missiles with Spatial Cooperation［J］. Acta Aeronautica et Astronautica Sinica， 2018， 39（10）： 322115.（in Chinese）

［10］ 宋俊紅， 宋申民， 徐勝利. 帶有攻擊角約束的多導彈協(xié)同制導律［J］. 中國慣性技術(shù)學報， 2016， 24（4）： 554-560.

Song Junhong， Song Shenmin， Xu Shengli. Cooperative Guidance Law for Multiple Missiles with Impact Angle Constraints［J］. Journal of Chinese Inertial Technology， 2016， 24（4）： 554-560.（in Chinese）

［11］ 譚詩利， 雷虎民， 王斌. 高超聲速目標攔截含攻擊角約束的協(xié)同制導律［J］. 北京理工大學學報， 2019， 39（6）： 597-602.

Tan Shili， Lei Humin， Wang Bin. Cooperative Guidance Law for Hypersonic Targets with Constrained Impact Angle［J］. Transactions of Beijing Institute of Technology， 2019， 39（6）： 597-602.（in Chinese）

［12］ Zhang Y A， Wang X L， Wu H L. A Distributed Cooperative Guidance Law for Salvo Attack of Multiple Anti-Ship Missiles［J］. Chinese Journal of Aeronautics， 2015， 28（5）： 1438-1450.

［13］ Zhao Q L， Dong X W， Liang Z X， et al. Distributed Cooperative Guidance for Multiple Missiles with Fixed and Switching Communication Topologies［J］. Chinese Journal of Aeronautics， 2017， 30（4）： 1570-1581.

［14］ 呂騰. 基于一致性的多巡航導彈協(xié)同末制導律設計［D］. 哈爾濱： 哈爾濱工業(yè)大學， 2019.

Lü Teng. Consensus Based Cooperative Terminal Guidance Law Design for Multiple Cruise Missiles［D］. Harbin： Harbin Institute of Technology， 2019. （in Chinese）

［15］ Wang L， Xiao F. Finite-Time Consensus Problems for Networks of Dynamic Agents［J］. IEEE Transactions on Automatic Control， 2010， 55（4）： 950-955.

［16］ Mei J， Ren W， Chen J. Distributed Consensus of Second-Order Multi-Agent Systems with Heterogeneous Unknown Inertias and Control Gains under a Directed Graph［J］. IEEE Transactions on Automatic Control， 2016， 61（8）： 2019-2034.

［17］ Chen L M， Li C J， Mei J E， et al. Adaptive Cooperative Formation-Containment Control for Networked Euler-Lagrange Systems without Using Relative Velocity Information［J］. IET Control Theo-ry & Applications， 2017， 11（9）： 1450-1458.

［18］ Bhat S P， Bernstein D S. Finite-Time Stability of Continuous Autonomous Systems［J］. SIAM Journal on Control and Optimization， 2000， 38（3）： 751-766.

［19］ Zarchan P. Tactical and Strategic Missile Guidance［M］. 6th ed. Reston， Virginia： American Institute of Aeronautics and Astronautics， 2012.

Cooperative Multi-Missile Guidance Research Considering

Communication Topology Switching

Abstract： A time-space cooperative guidance law based on switching strategy is proposed for the multi-missile cooperative strike problem under switching topology. The distributed guidance law is designed for the time constraint in combination with the consistency algorithm， and it is proved that the system converges in finite time based on Lyapunov theory and can achieve simultaneous strikes. For spatial constraints， the ballistic shaping guidance law is used to make each missile converge to the desired line of sight angle. The switching strategy is designed so that missiles can achieve both temporal and angular coordinated attacks. The simulation analysis verifies that the designed guidance law can achieve the flanking attack and angular constraint under the switching topology condition and the loss of one missile from the group.

Key words： cooperative guidance; switching topology; time constraint; angular constraint; guidance law; velocity uncontrollability