制導(dǎo)武器命中精度估計(jì)方法與檢驗(yàn)方法一致性研究

劉文超，李大偉，鄭小兵，李 曦

（解放軍91550 部隊(duì)，遼寧 大連 116084）

0 引言

命中精度直接決定了制導(dǎo)武器的精確打擊能力，是武器試驗(yàn)鑒定中重點(diǎn)考核的技術(shù)指標(biāo)之一。命中精度技術(shù)指標(biāo)通常采用圓概率誤差Cep（circle error probable）來表示，命中精度評定就是考核制導(dǎo)武器實(shí)際CEP 值是否滿足技術(shù)指標(biāo)要求［1］。但是受政治、經(jīng)濟(jì)、試驗(yàn)條件等因素的影響，制導(dǎo)武器試驗(yàn)樣本有限，一般為小子樣［2］。在小子樣條件下對命中精度指標(biāo)進(jìn)行評定，通常有兩種方法：一是命中精度估計(jì)方法，即在試驗(yàn)結(jié)束后，對試驗(yàn)樣本進(jìn)行統(tǒng)計(jì)分析，采用參數(shù)估計(jì)方法計(jì)算出CEP 值，常用的參數(shù)估計(jì)方法有點(diǎn)估計(jì)［3］、區(qū)間估計(jì)［4］等；二是命中精度檢驗(yàn)方法，即在試驗(yàn)開始前，依據(jù)指標(biāo)要求，利用假設(shè)檢驗(yàn)方法預(yù)先確定合格判據(jù)，比如常見的“n 發(fā)m 中”方案［5］。兩種評定方法在較多文獻(xiàn)中均有應(yīng)用，針對不同的考核對象，基于估計(jì)或檢驗(yàn)方法，提出了與之適應(yīng)的精度評定方法。文獻(xiàn)［6］采用命中精度估計(jì)方法，設(shè)計(jì)了命中精度評估系統(tǒng)，解決了空地導(dǎo)彈命中精度評估問題；文獻(xiàn)［7］采用命中檢驗(yàn)方法，提出了一種概率圓檢驗(yàn)方案，解決了制導(dǎo)武器命中精度的試驗(yàn)鑒定問題。命中精度估計(jì)方法和檢驗(yàn)方法在工程中有著不同程度的應(yīng)用，均能較好地解決命中精度評定問題。從工程應(yīng)用來看，兩種方法之間必然會(huì)存在一定的關(guān)聯(lián)性，而從理論基礎(chǔ)來看，兩種方法也存在固有的差異。目前，兩種評定方法往往獨(dú)立開展用于命中精度評定工作，很少對兩種評定方法之間的聯(lián)系和區(qū)別開展比對研究，一定程度上限制了命中精度評定方法的合理選擇和優(yōu)化設(shè)計(jì)。為此，本文在對小樣本條件下命中精度估計(jì)方法和檢驗(yàn)方法進(jìn)行分析的基礎(chǔ)上，從雙方風(fēng)險(xiǎn)一致性層面對兩種評定方法的一致性進(jìn)行系統(tǒng)研究，以發(fā)現(xiàn)兩種評定方法內(nèi)在的聯(lián)系與區(qū)別，為命中精度評定方案的合理選擇和優(yōu)化設(shè)計(jì)提供理論依據(jù)。

1 命中精度指標(biāo)評定分析

1.1 命中精度CEP 指標(biāo)

命中精度的指標(biāo)通常采用圓概率誤差CEP 描述，具體定義：以目標(biāo)點(diǎn)為圓心，落點(diǎn)分布概率為50%的圓域?qū)?yīng)的半徑。CEP 受系統(tǒng)誤差和隨機(jī)誤差的綜合影響，反映了落點(diǎn)相對目標(biāo)點(diǎn)的的總體偏離程度［8］。

CEP 可以用概率密度函數(shù)來表示，即以目標(biāo)點(diǎn)為原點(diǎn)建立二維平面直角坐標(biāo)系，假設(shè)落點(diǎn)縱向偏差X 和橫向偏差Z 服從二維正態(tài)分布，則CEP 滿足如下圓概率誤差一般方程。

式中，μX、μZ分別為縱、橫向偏差的均值；σX、σZ分別為縱、橫向偏差的標(biāo)準(zhǔn)差；ρ 為縱、橫向偏差相關(guān)系數(shù)；RCEP為圓概率誤差CEP 值。

式（1）為考慮縱、橫向偏差相關(guān)情況下的圓概率誤差一般方程。為簡化計(jì)算，通常將其轉(zhuǎn)換為縱、橫向偏差獨(dú)立情況下的圓概率誤差方程［9］，具體變換方法如下。

經(jīng)過上述變化，式（1）可變換為

1.2 CEP 指標(biāo)評定方法

制導(dǎo)武器命中精度評定是指對各類試驗(yàn)的結(jié)果進(jìn)行分析處理，以此來評價(jià)命中精度水平是否滿足指標(biāo)要求。由于試驗(yàn)子樣通常為小子樣，會(huì)影響評定結(jié)論的準(zhǔn)確性，因此，給使用方和研制方均帶來風(fēng)險(xiǎn)，即存在命中精度實(shí)際性能滿足要求而評定結(jié)論不合格的研制方風(fēng)險(xiǎn)，和命中精度實(shí)際性能不滿足要求而評定結(jié)論合格的使用方風(fēng)險(xiǎn)。目前，命中精度評定方法主要思路分為兩類。

1）命中精度估計(jì)方法。試驗(yàn)結(jié)束后根據(jù)試驗(yàn)樣本數(shù)據(jù)，按照命中精度CEP 的數(shù)學(xué)定義進(jìn)行評估計(jì)算，得出制導(dǎo)武器的CEP 估計(jì)值，將估計(jì)值與指標(biāo)要求進(jìn)行比較，給出評定結(jié)論。該方法的優(yōu)點(diǎn)是能夠給出命中精度具體數(shù)值，缺點(diǎn)是對試驗(yàn)子樣數(shù)有一定要求，且在試驗(yàn)過程中如果提前出現(xiàn)精度較差的情況，無法提前終止試驗(yàn)，造成試驗(yàn)資源浪費(fèi)。

2）命中精度檢驗(yàn)方法。試驗(yàn)開始前利用假設(shè)檢驗(yàn)的思想確定“n 發(fā)m 中”方案設(shè)計(jì)，試驗(yàn)過程中當(dāng)結(jié)果滿足方案要求時(shí)，終止試驗(yàn)。該方法的優(yōu)點(diǎn)是可節(jié)省試驗(yàn)樣本數(shù)量，缺點(diǎn)是無法給出命中精度具體數(shù)值。

2 命中精度估計(jì)方法分析

命中精度估計(jì)方法依據(jù)的是數(shù)理統(tǒng)計(jì)參數(shù)估計(jì)理論，可分為點(diǎn)估計(jì)和區(qū)間估計(jì)方法。點(diǎn)估計(jì)通常采用代入型點(diǎn)估計(jì)方法，考慮到實(shí)際評定時(shí)更關(guān)注命中精度上界是否滿足指標(biāo)要求，區(qū)間估計(jì)可采用參數(shù)自助法進(jìn)行區(qū)間上界估計(jì)。

2.1 估計(jì)方法

2.1.1 代入型點(diǎn)估計(jì)法

根據(jù)落點(diǎn)樣本（X1，X1），（X2，X2），…，（Xn，Xn）經(jīng)異常值檢測、正態(tài)性檢驗(yàn)后，可計(jì)算出樣本的均值、標(biāo)準(zhǔn)差和相關(guān)系數(shù)的估計(jì)值為

將上述估計(jì)值代入式（2）和式（3）替換μX、μZ、σX、σZ和ρ，通過數(shù)值積分方法［10］可求得圓概率誤差的點(diǎn)估計(jì)值。

2.1.2 區(qū)間上界估計(jì)參數(shù)自助法

參數(shù)自助法是利用已知小樣本數(shù)據(jù)統(tǒng)計(jì)特性進(jìn)行再抽樣，利用生成的再生樣本進(jìn)行統(tǒng)計(jì)分析［11-12］。具體步驟如下：

2）對每一組樣本分別采用代入型點(diǎn)估計(jì)方法進(jìn)行估計(jì)，獲得M 個(gè)圓概率誤差估計(jì)值，并從小到大進(jìn)行排列得到序列；

經(jīng)點(diǎn)估計(jì)和區(qū)間上界估計(jì)，當(dāng)估計(jì)值均滿足精度指標(biāo)要求時(shí)，評估結(jié)論為合格。

2.2 小子樣條件對命中精度估計(jì)方法的影響分析

考慮到制導(dǎo)武器試驗(yàn)子樣數(shù)量較小，受隨機(jī)性的影響，采用命中精度估計(jì)方法會(huì)影響評定結(jié)論的可信度，對研制方和使用方均產(chǎn)生風(fēng)險(xiǎn)［13］。因此，基于命中精度估計(jì)方法研究樣本數(shù)量對命中精度評定的影響，即通過蒙特卡洛仿真方法研究樣本數(shù)量對研制方風(fēng)險(xiǎn)和使用方風(fēng)險(xiǎn)的影響情況。設(shè)置仿真條件如下：假設(shè)命中精度指標(biāo)CEP 為10 m；橫向、縱向落點(diǎn)偏差均值均為0，標(biāo)準(zhǔn)差相等；實(shí)際精度CEP 在8～12 m 之間變化；試驗(yàn)樣本數(shù)量在7 到500之間變化；置信水平為0.80；每種情況仿真次數(shù)為10 000 次。估計(jì)方法的研制方風(fēng)險(xiǎn)α1和使用方風(fēng)險(xiǎn)β1可表示為

基于上述仿真條件分別采用點(diǎn)估計(jì)和區(qū)間上界估計(jì)法，可得研制方風(fēng)險(xiǎn)和使用方風(fēng)險(xiǎn)變化情況，如表1 和表2 所示。

表1 點(diǎn)估計(jì)方法雙方風(fēng)險(xiǎn)隨樣本數(shù)量的變化Table 1 Variation of risk for point estimation with sample number

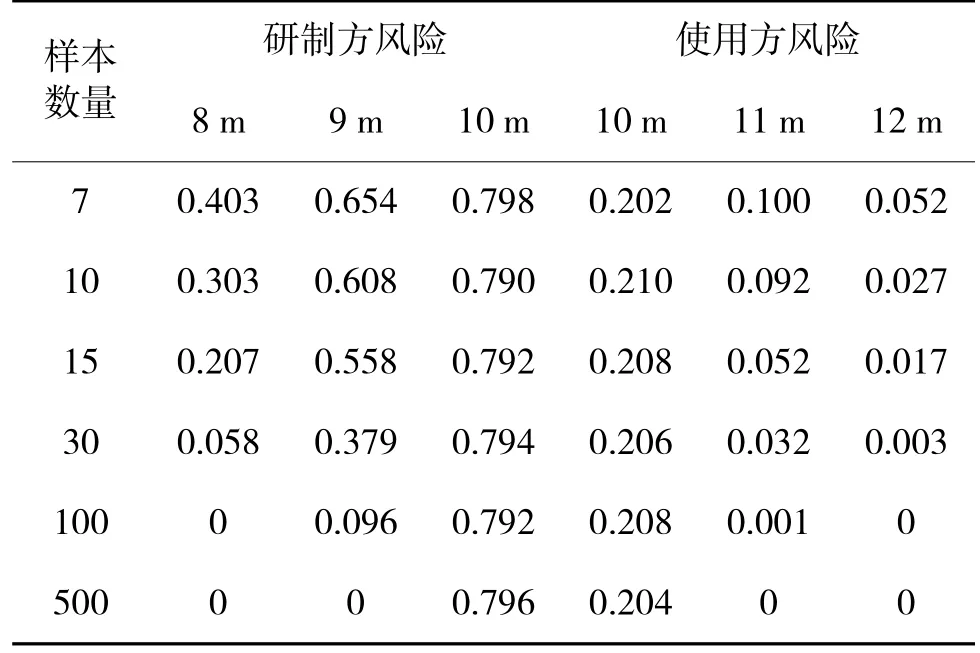
表2 區(qū)間上界估計(jì)方法雙方風(fēng)險(xiǎn)隨樣本數(shù)量的變化Table 2 Variation of risk for upper confidence bound estimation with sample numbe

從表1 和表2 可以看出，在武器性能一定的條件下，隨著樣本數(shù)量的增加，研制方風(fēng)險(xiǎn)和使用方風(fēng)險(xiǎn)均會(huì)減小；在樣本數(shù)量一定的條件下，武器命中精度滿足指標(biāo)要求且水平越高，研制方風(fēng)險(xiǎn)越小；相反，武器命中精度不滿足指標(biāo)要求且水平越低，使用方風(fēng)險(xiǎn)越小。通過增加樣本數(shù)量和提高武器自身精度性能水平, 可有效提升命中精度評定的準(zhǔn)確性，降低因樣本隨機(jī)性產(chǎn)生的雙方風(fēng)險(xiǎn)。特別的，當(dāng)命中精度水平與技術(shù)指標(biāo)相等時(shí)，如果采用點(diǎn)估計(jì)方法，研制方風(fēng)險(xiǎn)和使用方風(fēng)險(xiǎn)基本相當(dāng)，均為50%左右，雙方共同承擔(dān)試驗(yàn)風(fēng)險(xiǎn)。如果采用區(qū)間上界估計(jì)法，研制方風(fēng)險(xiǎn)為80%左右，使用方風(fēng)險(xiǎn)則為20%左右，滿足仿真設(shè)計(jì)條件，區(qū)間上限估計(jì)法對使用方更有利。一般情況下，命中精度指標(biāo)由使用方提出需求，在試驗(yàn)子樣受限的情況下，為了更好地滿足制導(dǎo)武器使用要求，通常采用區(qū)間上界估計(jì)方法進(jìn)行命中精度評定。

3 命中精度檢驗(yàn)方法分析

在小子樣條件下，可以利用數(shù)理統(tǒng)計(jì)假設(shè)檢驗(yàn)理論，進(jìn)行“n 發(fā)m 中”命中精度檢驗(yàn)方案設(shè)計(jì)，實(shí)際試驗(yàn)時(shí)滿足檢驗(yàn)方案即可停止試驗(yàn)。

3.1 檢驗(yàn)方法

檢驗(yàn)方法采用如下的統(tǒng)計(jì)假設(shè)［14］：

式中，H0為原假設(shè)，H1為備擇假設(shè)，λ 為檢出比（一般取1.2～2），需要根據(jù)制導(dǎo)武器的成熟水平由研制方和使用方共同確定。

設(shè)n 為總子樣數(shù)，m 為落入以R 為半徑的圓域內(nèi)的落點(diǎn)個(gè)數(shù)，則有

式中，P0為滿足原假設(shè)落入半徑為R 的圓中的概率；P1為滿足備擇假設(shè)的落入半徑為R 的圓中的概率。

假設(shè)落點(diǎn)個(gè)數(shù)檢驗(yàn)門限m*，則研制方和使用方風(fēng)險(xiǎn)分別為

在明確總子樣數(shù)n 和命中子樣數(shù)檢驗(yàn)門限m*基礎(chǔ)上，通過調(diào)整檢出比λ 和圓域半徑R 進(jìn)行檢驗(yàn)方案設(shè)計(jì)，使得使用方和研制方風(fēng)險(xiǎn)相當(dāng)，生成命中精度檢驗(yàn)方案［15-17］：當(dāng)m≥m*時(shí)，接受原假設(shè)，命中精度滿足指標(biāo)要求；否則命中精度不滿足指標(biāo)要求。

3.2 假設(shè)檢驗(yàn)與命中精度指標(biāo)關(guān)系的討論

由于命中精度指標(biāo)通常以具體數(shù)值的形式給出，并未明確對應(yīng)于式（6）假設(shè)檢驗(yàn)中的原假設(shè)還是備擇假設(shè)，因此，命中精度指標(biāo)值是CEP0還是CEP1需要予以明確。

針對上述問題開展具體分析：假設(shè)試驗(yàn)樣本數(shù)為7，命中精度指標(biāo)CEP 為10 m，檢出比λ 為1.5，分命中精度指標(biāo)為原假設(shè)和備擇假設(shè)兩種情況進(jìn)行檢驗(yàn)方案設(shè)計(jì)。按照雙方風(fēng)險(xiǎn)相等的原則，得到兩種情況下命中精度檢驗(yàn)方案，如表3 和表4 所示。

表3 精度指標(biāo)為原假設(shè)的檢驗(yàn)方案Table 3 Test scheme of accuracy index equal to original hypothesis

表4 精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方案Table 4 Test scheme of accuracy index equal to alternative hypothesis

從表3 和表4 可以看出，對比兩種情況下的檢驗(yàn)方案，在同一命中子樣數(shù)條件下，雖然雙方風(fēng)險(xiǎn)基本相同，但命中域半徑差別很大，顯然兩種方案用于精度評定，必然會(huì)導(dǎo)致較大差別的評定結(jié)論。

對兩種情況下評定方案的適應(yīng)性進(jìn)行研究。采用蒙特卡洛仿真進(jìn)行精度評定模擬，分別采用兩種檢驗(yàn)方案以及點(diǎn)估計(jì)、區(qū)間上界兩種估計(jì)方法進(jìn)行精度評定。設(shè)置仿真條件：命中精度指標(biāo)CEP 為10 m，實(shí)際精度CEP 分別取6 ～13 m，每次抽檢樣本數(shù)為7，仿真次數(shù)為10 000 次，檢驗(yàn)方案采用“7 發(fā)5中”方案，區(qū)間上界估計(jì)置信水平為0.8，可得不同精度評定方法的評定結(jié)果如下頁表5 所示。

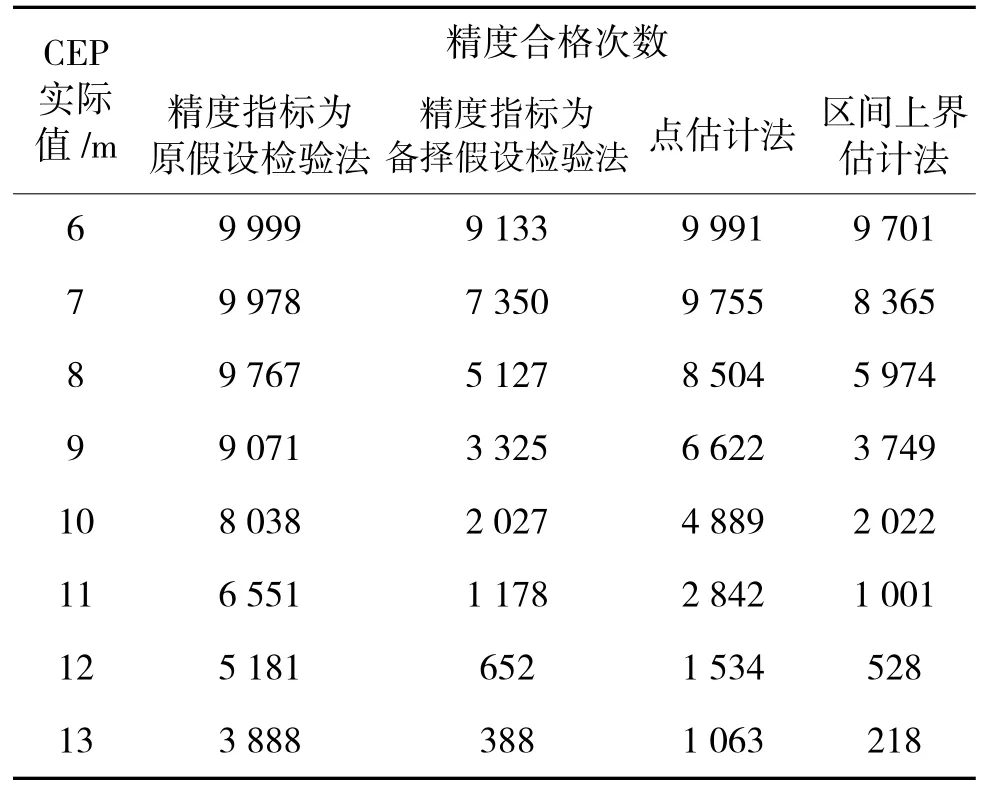
表5 4 種命中精度評定方法模擬仿真結(jié)果Table 5 Simulation of four hit accuracy evaluation methods

從表5 可以看出，從研制方風(fēng)險(xiǎn)角度來看，精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方案和區(qū)間上界估計(jì)研制方風(fēng)險(xiǎn)大致相當(dāng)且最大，點(diǎn)估計(jì)法次之，精度指標(biāo)為原假設(shè)的檢驗(yàn)方案研制方風(fēng)險(xiǎn)最小；從使用方角度來看，精度指標(biāo)為原假設(shè)的檢驗(yàn)方案使用方風(fēng)險(xiǎn)最大，點(diǎn)估計(jì)法次之，精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方案和區(qū)間上界估計(jì)使用方風(fēng)險(xiǎn)大致相當(dāng)且最小。因此，考慮命中精度估計(jì)方法通常采用區(qū)間上界估計(jì)方法，從雙方風(fēng)險(xiǎn)的一致性層面分析，檢驗(yàn)方法應(yīng)當(dāng)選擇精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方案。

4 估計(jì)方法和檢驗(yàn)方法的一致性分析

經(jīng)研究，命中精度估計(jì)方法采用區(qū)間上界估計(jì)方法，與精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方案在精度合格概率上具有較強(qiáng)的一致性，體現(xiàn)了兩種方法在雙方風(fēng)險(xiǎn)上的一致性。在制導(dǎo)武器性能一定和試驗(yàn)總樣本數(shù)量確定的基礎(chǔ)上，影響雙方風(fēng)險(xiǎn)大小的因素為：

1）區(qū)間上界估計(jì)方法中使用方和研制方風(fēng)險(xiǎn)主要受置信水平設(shè)置的影響。而置信水平受制導(dǎo)武器研制成熟水平的影響，由使用方和研制方共同確認(rèn)。在命中精度CEP 指標(biāo)為10 m、試驗(yàn)子樣為7、實(shí)際精度CEP 在6 ～13 m 之間變化條件下，不同置信水平（0.70～0.95）的雙方風(fēng)險(xiǎn)如表6 所示。

表6 不同置信水平下區(qū)間上界估計(jì)方法風(fēng)險(xiǎn)Table 6 Risk of upper confidence bound estimation under different confidence levels

2）精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方法中使用方和研制方風(fēng)險(xiǎn)主要受檢出比λ 設(shè)置的影響。同樣，檢出比受制導(dǎo)武器研制成熟水平的影響，由使用方和研制方共同確認(rèn)。在命中精度CEP 指標(biāo)為10 m、試驗(yàn)子樣為7 條件下，不同檢出比（1.3～1.8）的“7 發(fā)5 中”方案如表7 所示。基于設(shè)計(jì)方案，可得不同檢出比、實(shí)際精度CEP 在8～13 m 之間變化條件下的雙方風(fēng)險(xiǎn)如表8 所示。

表7 不同檢出比“7 發(fā)5 中”檢驗(yàn)方案Table 7 Five out of seven schemes under different detection ratios

表8 不同檢出比下檢驗(yàn)方法風(fēng)險(xiǎn)Table 8 Risk of test scheme under different detection ratios

從表6 可以看出，在各實(shí)際精度CEP 情況下，區(qū)間上界估計(jì)方法的雙方風(fēng)險(xiǎn)均隨置信水平1-α的變化而變化。從表7 和表8 可以看出，在各實(shí)際精度CEP 情況下，檢驗(yàn)方法的雙方風(fēng)險(xiǎn)均隨檢出比λ 的變化而變化。因此，在制導(dǎo)武器性能一定和試驗(yàn)總樣本數(shù)量確定的前提下，兩種方法雙方風(fēng)險(xiǎn)的控制體現(xiàn)在反映研制水平的參數(shù)設(shè)置上，可通過調(diào)整置信水平1-α 和檢出比λ，使得兩種評定方法達(dá)到控制雙方風(fēng)險(xiǎn)上的一致性。

下面結(jié)合數(shù)學(xué)仿真通過調(diào)整參數(shù)驗(yàn)證兩種方法的一致性。在命中精度CEP 指標(biāo)為10 m、試驗(yàn)子樣為7、實(shí)際精度CEP 在8 ～13 m 之間變化條件下，固定置信水平為0.8，通過調(diào)整檢出比使得估計(jì)方法和檢驗(yàn)方法雙方風(fēng)險(xiǎn)一致，結(jié)果如表9 所示。

表9 滿足評定方法一致性下置信水平和檢出比參數(shù)Table 9 Confidence level and detection ratio under conformity of assessment methods

從表9 可以看出，當(dāng)制導(dǎo)武器實(shí)際性能一定時(shí)，可以通過調(diào)整置信水平和檢出比，使得兩種評定方法雙方風(fēng)險(xiǎn)一致；當(dāng)固定置信水平時(shí)，隨著制導(dǎo)武器實(shí)際精度變化時(shí)，需要調(diào)整檢出比才能實(shí)現(xiàn)兩種方法雙方風(fēng)險(xiǎn)一致；同樣也可得出，當(dāng)固定檢出比時(shí)，隨著制導(dǎo)武器實(shí)際精度變化時(shí)，需要調(diào)整置信水平才能實(shí)現(xiàn)兩種方法雙方風(fēng)險(xiǎn)的一致。因此，置信水平和檢出比參數(shù)的對應(yīng)關(guān)系可為命中精度評定方法的設(shè)計(jì)提供依據(jù)。

在兩種評定方法滿足雙方風(fēng)險(xiǎn)一致性條件下采用蒙特卡洛仿真進(jìn)行精度評定模擬仿真。在命中精度CEP 指標(biāo)為10 m、試驗(yàn)子樣為7、實(shí)際精度CEP 在6 ～13 m 之間變化條件下，置信水平和檢出比滿足一致性設(shè)置條件，仿真次數(shù)為10 000 次，可得精度評定結(jié)果如表10 所示。

表10 滿足評定方法一致性下精度評定模擬仿真Table 10 Simulation of hit accuracy evaluation under conformity of assessment methods

從表10 可以看出，在置信水平和檢出比滿足一致性設(shè)置條件基礎(chǔ)上，兩種評定方法命中精度合格次數(shù)基本相當(dāng)，反映了兩種方法在雙方風(fēng)險(xiǎn)層面上的一致性。因此，進(jìn)行命中精度評定時(shí)，在研制方和使用方依據(jù)風(fēng)險(xiǎn)共同確定某一參數(shù)的基礎(chǔ)上，根據(jù)武器性能先驗(yàn)信息或者命中精度指標(biāo)，通過上述仿真分析方法，可以得出另一個(gè)參數(shù)的合理設(shè)置值或范圍。特別的，對已經(jīng)過精度評估的制導(dǎo)武器進(jìn)行批次檢驗(yàn)時(shí)，可以根據(jù)之前的評估結(jié)果，通過上述仿真分析方法得出合理檢出比，用于制導(dǎo)武器的批次檢驗(yàn)結(jié)果評定。

由于兩種評定方法分別基于參數(shù)估計(jì)和假設(shè)檢驗(yàn)的不同理論基礎(chǔ)，對于相同試驗(yàn)結(jié)果進(jìn)行精度評定會(huì)存在評定結(jié)論不一致的現(xiàn)象，不一致的概率與制導(dǎo)武器實(shí)際研制水平有關(guān)。因此，兩種評定方法不能同時(shí)使用于命中精度評定，以避免出現(xiàn)結(jié)論不一致的問題，進(jìn)行試驗(yàn)之前需結(jié)合兩種評定方法的優(yōu)缺點(diǎn)和試驗(yàn)設(shè)計(jì)需求選擇確定評定方法。

5 結(jié)論

以制導(dǎo)武器命中精度估計(jì)方法和檢驗(yàn)方法為研究對象，在詳細(xì)分析小子樣條件對估計(jì)方法影響，以及命中精度指標(biāo)與檢驗(yàn)方法關(guān)系基礎(chǔ)上，明確了區(qū)間上界估計(jì)方法和精度指標(biāo)為備擇假設(shè)的檢驗(yàn)方法兩種典型應(yīng)用方法，通過合理調(diào)整置信水平和檢出比參數(shù)，可以實(shí)現(xiàn)兩種方法雙方風(fēng)險(xiǎn)的一致性，同時(shí)由于兩種方法理論基礎(chǔ)不同，進(jìn)行精度評定會(huì)存在一定概率結(jié)論不一致的現(xiàn)象。該研究可為命中精度評定方法的合理選擇和優(yōu)化設(shè)計(jì)提供依據(jù)。