排巖機履帶行走裝置接地比壓分布規律研究

燕碧娟，劉澤坤，王志霞，寇保福

（太原科技大學機械工程學院，山西 太原 030024）

1 引言

排巖機常用于露天礦半連續開采中[1-2]，其工作環境復雜且惡劣。當接地比壓大于其所接觸地面承載力時，地面常會發生不均勻沉降，甚至是壓潰，導致設備可靠性變差，進而發生傾覆。因此，為保證排巖機工作的安全性，實際工程中需提前對地基進行處理[3]。

同時，接地比壓對排巖機履帶行走裝置的移動性能、牽引性能、土壤的變形的改善都十分重要[4]。由此可見，對排巖機履帶行走裝置分布接地比壓進行研究是十分必要的。

目前，國內外學者針對接地比壓進行了大量研究。如：文獻[5]以掘進機為研究對象，對其橫擺截割工況下的履帶接地比壓進行了研究。文獻[6]將履帶板假設為剛體、土地假設為柔體，考慮了重心沿履帶行走裝置行走方向與垂直于履帶行走裝置行走方向的偏心距，推導出接地比壓計算公式。文獻[7]將彈性地基上的履帶架假設為連續梁，得到了履帶式起重機的接地比壓的計算模型。文獻[8]運用矢量分析理論和達朗伯原理建立了接地比壓為線性分布數學模型，并進行了實例分析證明了它的實際的指導意義。然而，通過大量文獻查閱可知，有關排巖機接地比壓的研究甚少。

考慮到排巖機受料臂的旋轉、排料臂的上仰、回轉支承的旋轉均會對排巖機整機接地比壓造成不同程度的影響，因此欲通過上述因素對排巖機重心位置的改變，進而研究接地比壓的分布規律，從而為整機的設計及地基的處理提供一定的參考。

2 履帶接地比壓數學模型建立

排巖機履帶接地比壓是指其接地部分單位面積上承受的縱向載荷[9]。建立如圖1所示空間直角坐標系（y軸正方向為履帶行駛方向，z軸正方向垂直地面向下），假設履帶為剛體，工作地基為理想彈性體，此時接地比壓為線性分布[10-12]，如圖1 所示。其中Pmax、Pmin分別為接地比壓最大值及最小值。

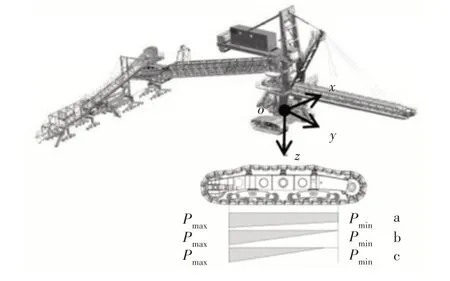
圖1 排巖機接地比壓分布示意圖Fig.1 Diagram of Ground Specific Pressure Distribution of Crawler Device

當整機實際工作重心與其理想幾何重心重合時，履帶接地比壓呈均布狀態，此時平均接地比壓Pave：

式中：Gi—排巖機各個部分的重量，其中包括物料的重量；b—履帶寬度；L—履帶接地部分長度；n—履帶條數。

當排巖機整機工作重心偏離其幾何中心時［13］，設此時的重心空間坐標為（xg’，yg’，zg’），當|yg’|≤L/6時，如圖1（a）所示。接地比壓分布呈現梯形分布。假設重心靠近左側履帶，排巖機整機自身重力以及沿z軸方向外載荷所構成的合力分布情況為：

式中：B—履帶行走裝置中心距。以左履帶為例，履帶最大接地比壓Plmax、最小接地比壓Plmin為：

式中：Gl—排巖機左側履帶所承受的載荷；W—履帶接地平面模量；L—履帶接地長度。進一步根據履帶相應的幾何關系可以得出左側履帶接地段上任意一點接地比壓Pl（y）為：

同理可得右側履帶最大接地比壓Prmax、最小接地比壓Prmin，以及其上任意點接地比壓。

當|yg’|≤L∕6時，如圖1（b）、圖1（c）所示。接地比壓呈三角形分布，仍以左側履帶為例，其平均接地比壓為Plave：

最小接地比壓Plmin為0，最大接地比壓Plmax為：

根據接地比壓計算數學模型，排巖機履帶行走裝置接地比壓除了跟自身重量、履帶接地長度、履帶寬度、履帶中心距有關系外，還跟重心的位置有關系。

3 計算結果分析

3.1 排巖機重心坐標的確定

排巖機受料臂的旋轉，旋轉角α范圍：（-125～125）°、排料臂的上仰，上仰角β范圍：（-6～13）°，及回轉支承的旋轉會影響重心的坐標，進而影響排巖機整機接地比壓，因此，有必要先確定上述各因素下排巖機重心位置[14]。

受料臂旋轉角度每隔10°、排料臂上仰角度每隔1°的散點圖，如圖2所示。

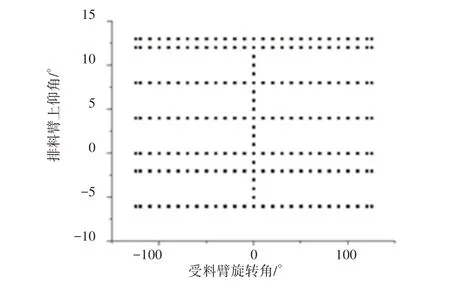
圖2 排料臂上仰角度、受料臂旋轉角度取值Fig.2 The Uptilt Angle of the Discharging Arm and the Rotation Angle of the Receiving Arm Are Calculated

因排巖機結構復雜不規則，難以推導其重心位置，故使用Solidworks 中質量屬性，自動計算圖2 共202 個取值點的重心坐標，如圖3所示。

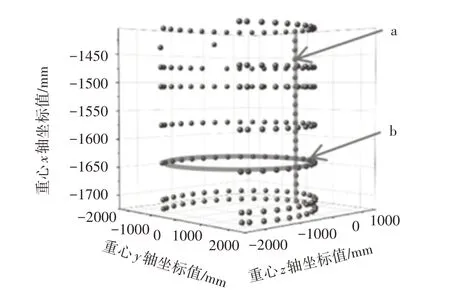
圖3 重心散點圖Fig.3 Scatter Diagram of the Center of Gravity

由圖3可以看出隨著受料臂的旋轉和排料臂的上仰，排巖機的重心空間分布呈現近似圓柱面的形狀。當排巖機排料臂上仰角固定，受料臂旋轉時，其重心呈近似環形，在x軸方向以及y軸方向上變化尤為明顯。當排巖機受料臂旋轉角固定，排料臂在（-6～13）°上仰時，其重心呈近似直線，在z軸方向變化尤為明顯。

為掌握排巖機重心位置隨受料臂旋轉角、排料臂旋上仰角變化情況，使用MATLAB 中curve fitting tool對圖2及圖3數據進行擬合，擬合結果如下：

擬合曲面，如圖4所示。圖中黑點表示重心空間坐標值與其對應的受料臂旋轉角度、排料臂旋上仰角度。通過圖4可以看出黑點基本都在擬合曲面上，且擬合的確定系數均高于0.9996。

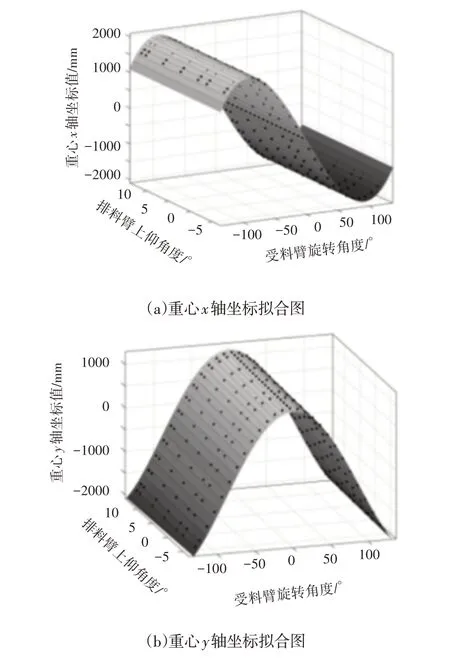
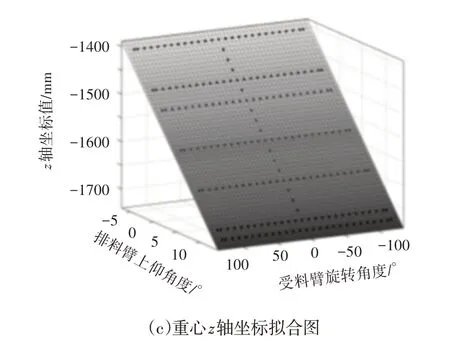
圖4 重心擬合曲面圖Fig.4 The Center of Gravity Fitting Surface Figure

設未考慮車體回轉支承旋轉角的重心坐標為（xg，yg，zg），當車體回轉支承旋轉角γ發生變化時，由排巖機整機結構可以發現，重心的空間z軸坐標不會發生變化，而x軸坐標和y軸坐標會圍繞o點旋轉相同的角度。

所得到的新的考慮車體回轉支承旋轉角后的重心空間坐標（xg’，yg’，zg’）計算過程為式（11）、式（12）。

3.2 接地比壓計算分析

以國內某型排巖機為研究對象，通過查閱該型排巖機的產品手冊以及技術圖紙，確定各個主要參數數值，如表1所示。

表1 計算參數Tab.1 Calculating Parameter

取排巖機不同的受料臂旋轉角、排料臂上仰角、回轉支承旋轉角下的計算實例，如表2所示。相應計算結果，如表3所示。通過表3可以得到，6組實例中排巖機接地比壓最大值為0.443MPa、最大接地比壓最小值為0.171MPa，均超過了通過計算得到的平均接地比壓0.140MPa。另外，排巖機最小接地比壓最大值為0.109MPa，最小值為0MPa。

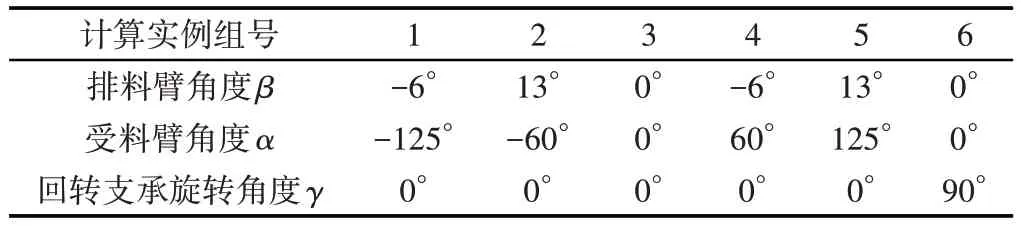
表2 各計算實例參數設置Tab.2 Parameters Settings of Each Calculation Example

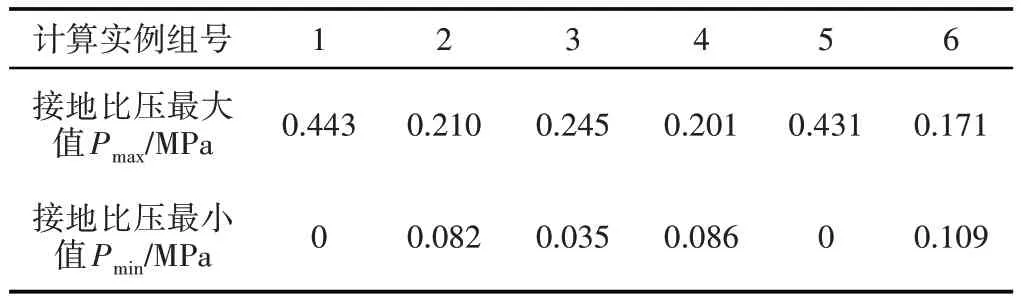
表3 各計算實例計算結果Tab.3 The Results of Each Calculation Instance

同時，為了驗證上述計算結果的正確性，在ANSYS Workbench 的Static Structural模塊中，對上述各個實例排巖機接地比壓分布進行仿真分析[15-16]，如圖5所示。從中可知，排巖機接地比壓分布呈現近似線性，接地比壓最值出現在履帶接地端的前端及后端，主要原因是在接地比壓數學模型中接地比壓沿行駛方向線性遞減或增加，因此接地比壓最值會出現在上述位置。接地比壓理論計算與仿真分析對比數值，如表4所示。

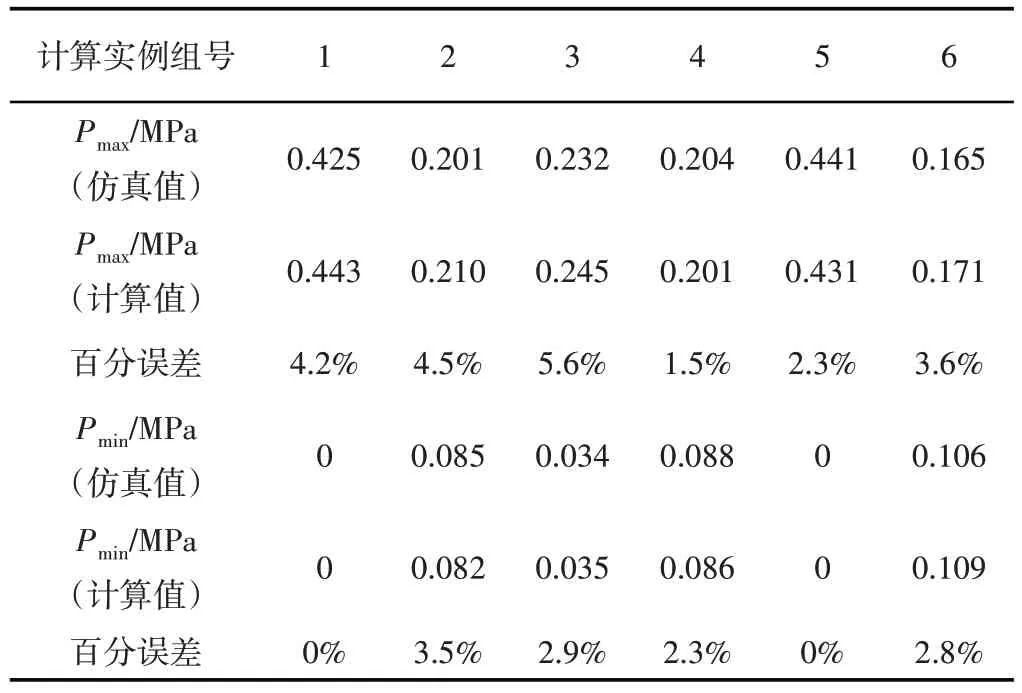
表4 接地比壓計算與仿真結果對比表Tab.4 Comparison Table of Ground Specific Pressure Calculation and Simulation Results

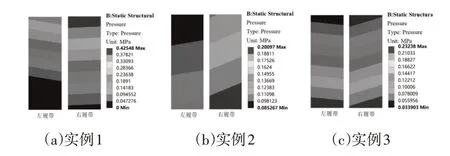
圖5 接地比壓分布云圖Fig.5 Ground Specific Pressure Distribution Nephogram

通過表4可知：6組實例中最大百分誤差為5.6%，最小百分誤差為0%，該結果驗證了第二小節所建履帶接地比壓數學模型的正確性。當排巖機回轉支承不旋轉時，在MATLAB中，利用提出的履帶接地比壓數學模型以及對重心的研究，編寫計算程序，得到排巖機最大接地比壓隨受料臂旋轉角度、排料臂上仰角度的變化趨勢，如圖6所示。最小接地比壓變化趨勢，如圖7所示。

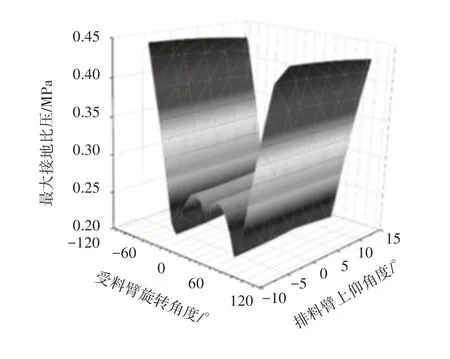
圖6 最大接地比壓隨受料臂旋轉角度、排料臂上仰角度趨勢圖Fig.6 The Trend Diagram of the Maximum Ground Pressure with the Rotation Angle of the Receiving Arm and the Elevation Angle of the Discharging Arm

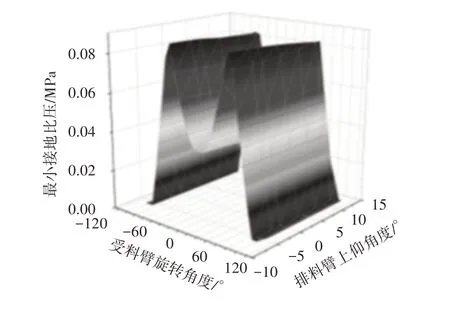
圖7 最小接地比壓隨受料臂旋轉角度、排料臂上仰角度趨勢圖Fig.7 Trend Diagram of the Minimum Ground Pressure with the Rotation Angle of the Receiving Arm and the Uptilt Angle of the Discharging Arm

通過圖6可知：排巖機最大接地比壓隨受料臂旋轉角度、排料臂上仰角度的變化趨勢呈現近似“W”型，其中最大接地比壓最大值為0.443MPa，出現在圖的兩側即受料臂旋轉角度絕對值最大時，最大接地比壓最小值為0.20MPa，出現在受料臂旋轉角度絕對值為60°附近。固定受料臂旋轉角度，圖形呈現近似直線，說明排料臂上仰角度對最大接地比壓值影響不大、最大接地比壓值主要受受料臂旋轉角度的影響。

從圖7可以看出：排巖機最大接地比壓隨受料臂旋轉角度、排料臂上仰角度的變化趨勢呈現近似“M”型；其中最小接地比壓最小值為0MPa，出現在圖的兩側，最小接地比壓最大值出現在受料臂旋轉角度絕對值為60°附近。固定受料臂旋轉角度，圖形呈現近似直線，說明排料臂上仰角度對最小接地比壓值影響不大、最小接地比壓值主要受受料臂旋轉角度的影響。

通過圖6、圖7所示。可以發現兩圖的變化呈現近似相反的趨勢，當排巖機最大接地比壓最大時，最小接地比壓也為最小值，當排巖機最大接地比壓最小時，最小接地比壓也為最大值。

4 結論

對排巖機受料臂的旋轉、排料臂的上仰、回轉支承的旋轉對履帶裝置接地比壓的影響進行了研究，所得主要結論如下：

（1）隨著受料臂的旋轉和排料臂的上仰，排巖機的重心空間分布呈現近似圓柱面的形狀。當排料臂上仰角固定，受料臂旋轉時，其重心呈近似環形。當排料臂在（-6～13）°上仰時，其重心呈近似直線。

（2）建立了履帶接地比壓數學模型，通過計算實例的仿真分析，驗證了其正確性。同時，各實例中接地比壓最大值為0.443MPa，超過了排巖機平均接地比壓0.140MPa，說明了排巖機平均接地比壓不能代替排巖機接地比壓分布情況。另外，仿真發現，排巖機接地比壓最值一般出現在履帶接地端的前后端。

（3）固定排巖機車體回轉支承旋轉角度后，排巖機履帶行走裝置接地比壓最大值隨排巖機受料臂旋轉角度的增加呈現“W”型變化趨勢，排巖機履帶行走裝置接地比壓最小值隨排巖機受料臂旋轉角度的增加呈現“M”型變化趨勢。