混聯(lián)機器人關(guān)節(jié)間隙誤差建模及其定位精度可靠性分析

郭天宇 張德權(quán) 吳錦輝 周鵬飛 孟原

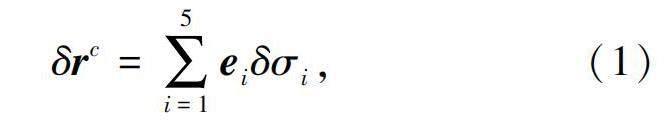
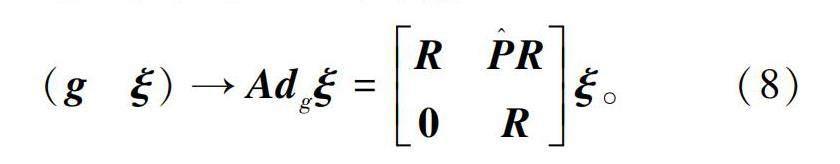
摘要：機器人末端定位精度可靠性是衡量其精度性能的重要指標(biāo)，關(guān)節(jié)間隙是影響機器人定位精度的主要因素之一，建立準(zhǔn)確的機器人定位精度誤差模型是進(jìn)行可靠性分析的前提。為探究空間關(guān)節(jié)間隙的隨機不確定性對含有閉鏈機構(gòu)混聯(lián)機器人定位誤差的影響規(guī)律，本文運用旋量理論和D-H參數(shù)法，提出一種考慮關(guān)節(jié)間隙的混聯(lián)機器人定位精度誤差模型；根據(jù)關(guān)節(jié)間隙模型參數(shù)的約束條件，量化間隙模型參數(shù)的不確定性，建立混聯(lián)機器人定位精度的可靠性模型；采用雙變量降維方法和鞍點近似方法，擬合機器人單坐標(biāo)定位誤差的概率密度函數(shù)，實現(xiàn)混聯(lián)機器人定位精度高效可靠性分析。以含有平行四邊形閉鏈機構(gòu)的建筑機器人為例，驗證所提模型的準(zhǔn)確性和工程適用性，結(jié)果表明所提方法對比于傳統(tǒng)的蒙特卡洛方法極大地提高了效率。

關(guān)鍵詞：混聯(lián)機器人；定位精度；關(guān)節(jié)間隙；不確定性；可靠性分析

中圖分類號：TP242文獻(xiàn)標(biāo)識碼：ADOI：10.3969/j.issn.1007-791X.2024.01.0030

引言

機器人末端執(zhí)行器的位置精度是機器人重要的性能指標(biāo)之一，定義為末端執(zhí)行器實際位置與期望位置的偏差[1]。產(chǎn)生偏差的主要原因是機器人存在潛在不確定性，如加工誤差[2-3]、裝配誤差[4]、關(guān)節(jié)間隙[5]等。其中關(guān)節(jié)間隙作為不可避免的不確定性因素嚴(yán)重影響機器人末端定位精度。

關(guān)節(jié)間隙模型依據(jù)工作空間可分為平面關(guān)節(jié)間隙模型[6-7]和空間關(guān)節(jié)間隙模型[8]。針對平面關(guān)節(jié)間隙模型，Ting等[6]利用虛擬桿件法求解四連桿機構(gòu)誤差邊界，分析含轉(zhuǎn)動關(guān)節(jié)和移動關(guān)節(jié)的連桿機構(gòu)間隙疊加對其輸出位置的影響。Chen和Gao[9]提出考慮具有轉(zhuǎn)動間隙的多桿機構(gòu)動態(tài)精度可靠度建模與計算方法，研究驅(qū)動速度、間隙值和間隙處摩擦系數(shù)在不同變化范圍內(nèi)對機構(gòu)動態(tài)精度可靠性的影響。Zhan等[10]將關(guān)節(jié)間隙參數(shù)設(shè)為區(qū)間變量，將其他參數(shù)設(shè)為隨機變量，針對具有區(qū)間變量和隨機變量的機械臂，提出一種新的混合可靠性分析方法。由于多環(huán)閉鏈機構(gòu)存在閉環(huán)耦合和結(jié)構(gòu)復(fù)雜等不利因素，趙強強等[11]提出一種用于多環(huán)閉鏈機構(gòu)的建模方法，該方法通過分析精度模型和誤差源概率分布類型，實現(xiàn)了多環(huán)閉鏈機構(gòu)誤差空間分析。上述間隙模型都基于平面模型，但機器人在工作過程中由于磨損等因素可能會產(chǎn)生徑向間隙，故需要分析空間關(guān)節(jié)間隙模型。

對于空間關(guān)節(jié)間隙模型，區(qū)間分析和優(yōu)化技術(shù)是常用的分析工具。Briot和Bonev[8]將區(qū)間分析方法應(yīng)用于三自由度平面并聯(lián)機器人的精度分析。Zhao等[12]提出一種計算并聯(lián)機構(gòu)誤差空間的封閉式方法，將關(guān)節(jié)間隙、輸入不確定性和制造缺陷引起的局部位姿偏差定義為運動群上的高斯分布，能夠快速預(yù)測末端執(zhí)行器位姿誤差分布的協(xié)方差和均值。侯雨雷等[13]考慮運動副間隙和桿件柔性對3PSS/S并聯(lián)機構(gòu)進(jìn)行軌跡仿真，采用模糊神經(jīng)網(wǎng)絡(luò)綜合誤差預(yù)估模型進(jìn)行誤差預(yù)估。Frisoli等[14]提出一種基于旋量理論的帶轉(zhuǎn)動關(guān)節(jié)間隙空間并聯(lián)機器人位置精度分析方法，利用優(yōu)化技術(shù)來搜索最大偏差。Wu等[15]利用傳統(tǒng)的線性正微分運動學(xué)對3PPR并聯(lián)機器人進(jìn)行誤差建模，然后通過優(yōu)化得到關(guān)節(jié)間隙方面的誤差矢量最大幅值。Meng和Ze[16]基于旋量理論提出一種并聯(lián)機器人誤差分析的通用方法，通過將誤差計算轉(zhuǎn)化為優(yōu)化問題能夠有效求得誤差最大值。然而，由于不同參數(shù)不確定性和包裹效應(yīng)的相互作用[17]，區(qū)間分析方法在本質(zhì)上高估了誤差范圍，求解可靠性不準(zhǔn)確。對于優(yōu)化方法，一旦約束條件變得不規(guī)則，很難尋求全局最優(yōu)解，即使得到了最優(yōu)結(jié)果，也只是提供了最大的位置和方向偏差，而誤差分布類型未知，無法分析可靠性。

矩方法[18]是一種可以同時得到目標(biāo)函數(shù)概率分布和可靠度的方法，不需計算設(shè)計點和功能函數(shù)的導(dǎo)數(shù)，因此受到很多學(xué)者關(guān)注。Zhang和Han[1]將機器人連桿尺寸和關(guān)節(jié)轉(zhuǎn)角考慮為正態(tài)分布不確定性變量，并基于鞍點近似分析機器人的單點定位精度可靠性。Wu等[19]利用點估計方法對工業(yè)機器人定位精度可靠性進(jìn)行有效評估。上述可靠性分析方法雖然效率和精度較高，但沒有對空間關(guān)節(jié)間隙進(jìn)行具體分析。

根據(jù)上述問題，針對由空間關(guān)節(jié)間隙引起的混聯(lián)機器人末端定位精度誤差，結(jié)合可靠性分析方法，開展串聯(lián)機器人誤差模型和閉鏈機構(gòu)誤差模型的研究；通過對模型進(jìn)行不確定性度量，提出關(guān)節(jié)間隙模型參數(shù)新分布；考慮關(guān)節(jié)處全方向誤差，通過降維積分方法計算定位誤差的前四階矩，通過鞍點近似方法分析定位精度的可靠性。

1基本理論

1.1關(guān)節(jié)間隙模型

空間轉(zhuǎn)動關(guān)節(jié)間隙如圖1所示，關(guān)節(jié)間隙的存在使得關(guān)節(jié)處產(chǎn)生微小誤差，關(guān)節(jié)間隙在關(guān)節(jié)處引起誤差如下[20]：

式中，ei（i=1，2，…，5）表示除繞轉(zhuǎn)動副軸線外其余五個方向運動的基向量，δσ1、δσ2和δσ3表示沿x、y和z軸的位移誤差，δσ4和δσ5表示繞x和y軸的轉(zhuǎn)動誤差。

由于關(guān)節(jié)間隙結(jié)構(gòu)的約束，當(dāng)機構(gòu)在關(guān)節(jié)處產(chǎn)生微小位移時，在銷軸軸向方向的位移需要小于等于εa，徑向方向需要小于等于εr，即

1.2D-H參數(shù)法與旋量理論

D-H參數(shù)法[19]過程簡單且便于理解，旋量理論[22]可直觀描述剛體運動的幾何特點，故本文采用D-H參數(shù)進(jìn)行機器人運動學(xué)分析，采用旋量理論分析關(guān)節(jié)間隙模型參數(shù)對機器人末端定位精度的影響。值得注意的是分析各關(guān)節(jié)微小誤差對機器人末端定位精度影響時，要在每個關(guān)節(jié)處都建立慣性坐標(biāo)系，機器人末端位姿在關(guān)節(jié)處慣性坐標(biāo)系上可表示為

式中，Ti0為第i個關(guān)節(jié)處的慣性坐標(biāo)系到D-H參數(shù)坐標(biāo)系的變換矩陣。

剛體空間位置的變化可表示為繞某直線的轉(zhuǎn)動加平行于該直線的移動。設(shè)動坐標(biāo)系為B，靜坐標(biāo)系為A，剛體在A系上的位姿變換矩陣可表示為[22]

式中，SE（3）為位姿變換的特殊歐式群；R為姿態(tài)變換矩陣；SO（3）為三維旋轉(zhuǎn)矩陣構(gòu)成的特殊正交群；P為位置矢量；R3為三維向量空間。

若剛體繞軸線ω=［ωx，ωy，ωz］T∈R3轉(zhuǎn)動θ角度，則剛體轉(zhuǎn)動的矩陣指數(shù)表示為

在純轉(zhuǎn)動情況下，剛體旋轉(zhuǎn)可用矩陣指數(shù)表示為

伴隨變換是指李代數(shù)的一個剛體平移，對于給定變換g=（P，R）∈SE（3），g的伴隨矩陣為

上文介紹了空間關(guān)節(jié)間隙模型、D-H參數(shù)法和旋量理論基礎(chǔ)；后續(xù)結(jié)合上述理論建立在關(guān)節(jié)間隙影響下含有閉鏈機構(gòu)的混聯(lián)機器人末端定位誤差模型，并對模型中的參數(shù)進(jìn)行不確定性度量。

2混聯(lián)機器人關(guān)節(jié)間隙誤差建模

2.1串聯(lián)機構(gòu)間隙誤差

如圖3所示，設(shè)機器人末端的坐標(biāo)為（x，y，z），由關(guān)節(jié)間隙引起機器人末端定位誤差為

式中，δE1、δE2和δE3表示機器人末端沿x、y和z軸的平移誤差；δE4、δE5和δE6表示關(guān)節(jié)間隙引起的機器人末端繞x、y和z軸的轉(zhuǎn)動誤差。

轉(zhuǎn)動關(guān)節(jié)軸線與基礎(chǔ)坐標(biāo)系的z軸不共線時，利用旋量理論計算局部坐標(biāo)系的伴隨變換矩陣，可分析任意關(guān)節(jié)處微小誤差對末端的影響。如圖4所示，轉(zhuǎn)動副繞基礎(chǔ)坐標(biāo)系x軸轉(zhuǎn)動，建立基礎(chǔ)坐標(biāo)系g（x，y，z）和局部坐標(biāo)系g0（x0，y0，z0）。在給定局部坐標(biāo)系的位姿后，由于其轉(zhuǎn)動軸線過原點，因此q=000T，轉(zhuǎn)動副的軸線方向ω=100T，該轉(zhuǎn)動副相對應(yīng)的運動旋量為

局部坐標(biāo)系到基礎(chǔ)坐標(biāo)系的位姿轉(zhuǎn)換矩陣為

根據(jù)式（7）和（8）可得g對應(yīng)的伴隨矩陣為

基礎(chǔ)坐標(biāo)系下機器人末端位置坐標(biāo)為（x， y， z），由式（19）可知，基礎(chǔ)坐標(biāo)系下的關(guān)節(jié)間隙對機器人末端的影響可由下式求解：

當(dāng)已知伴隨變換矩陣和機器人末端位置坐標(biāo)，則關(guān)節(jié)間隙對機器人末端定位精度的影響矩陣可表示為

M=U·Adg，（14）

則單個關(guān)節(jié)間隙導(dǎo)致的機器人末端定位誤差為

式中，串聯(lián)機器人關(guān)節(jié)受電機驅(qū)動，繞轉(zhuǎn)動副轉(zhuǎn)動的轉(zhuǎn)動誤差為0，即δσ6=0。

在工程實踐中，若已知關(guān)節(jié)轉(zhuǎn)動副軸線方向和局部坐標(biāo)系的轉(zhuǎn)換矩陣，可求解伴隨變換矩陣，然后根據(jù)本文提出的影響矩陣M分析任意關(guān)節(jié)間隙對機器人末端位置誤差的影響。

2.2閉鏈機構(gòu)間隙誤差

相比于串聯(lián)機器人，閉鏈機構(gòu)中關(guān)節(jié)更多，關(guān)節(jié)間隙對機構(gòu)精度影響更復(fù)雜。本節(jié)以平行四邊形閉鏈機構(gòu)為例，分析關(guān)節(jié)間隙對閉鏈機構(gòu)的影響。平行四邊形機構(gòu)坐標(biāo)系建模如圖5所示，與串聯(lián)機器人不同，平行四邊形共有4個關(guān)節(jié)，其中R11為主動關(guān)節(jié)，其余都為被動關(guān)節(jié)，需要獲得R12、R21和R22繞轉(zhuǎn)動副軸線的轉(zhuǎn)動誤差。如圖6所示，平行四邊形機構(gòu)可看作由兩個串聯(lián)機構(gòu)組成的閉鏈機構(gòu)。

設(shè)Mg11、Mg12、Mg21和Mg22分別為R11、R12、R21和R22處關(guān)節(jié)間隙對機器人定位精度的影響矩陣，則關(guān)節(jié)處間隙模型可表示為

式中，δσij為第i條支鏈的第j個關(guān)節(jié)的間隙模型。設(shè)Bij為第i條支鏈的第j個關(guān)節(jié)所對應(yīng)的變換矩陣，

δrij為第i條支鏈的第j個關(guān)節(jié)間隙模型對應(yīng)的前5個關(guān)節(jié)參數(shù)，

被動關(guān)節(jié)繞轉(zhuǎn)動副軸線的旋轉(zhuǎn)誤差設(shè)為δΘ1=δσ126和δΘ2=δσ216δσ226T，可計算平行四邊形兩條支鏈的誤差為

δEi=Bi·dri+Ji·δΘi（i=1，2）。 ???（21）

由幾何約束可知，關(guān)節(jié)間隙引起的兩條支鏈交點的誤差需相等，聯(lián)立方程可得

通過式（24）可求解R12沿運動副軸線轉(zhuǎn)動的旋轉(zhuǎn)誤差為

當(dāng)機器人含有閉鏈機構(gòu)時，可通過上述方法分析該機構(gòu)中被動關(guān)節(jié)繞轉(zhuǎn)動副軸線的轉(zhuǎn)動誤差，進(jìn)而獲得關(guān)節(jié)間隙對含有平行四邊形機構(gòu)的混聯(lián)機器人末端定位精度誤差模型。

2.3關(guān)節(jié)間隙參數(shù)不確定性度量

由1.1節(jié)可知，關(guān)節(jié)間隙模型各參數(shù)的上下界如式（3）所示，設(shè)εr=1mm，εa=0.5mm，各參數(shù)的統(tǒng)計信息如表1所示。

由于關(guān)節(jié)間隙的存在，參數(shù)之間應(yīng)滿足式（2）的約束方程。對模型中參數(shù)進(jìn)行不確定性度量，以表1中均值和標(biāo)準(zhǔn)差生成樣本點代入約束方程，將符合約束條件的樣本點提取出來，提取后樣本點的統(tǒng)計信息如表2所示。本文采用3種蒙特卡洛模擬法（Monte Carlo Simulation， MCS），分別是新分布的MCS、原始分布的MCS和考慮約束的MCS。其中新分布的MCS為以約束后均值和約束后標(biāo)準(zhǔn)差生成樣本；原始分布的MCS以原始均值和原始標(biāo)準(zhǔn)差生成樣本；考慮約束的MCS為將服從約束的樣本點為樣本。

在實際工程中，關(guān)節(jié)參數(shù)模型中各個參數(shù)應(yīng)滿足約束方程，因此將考慮約束MCS的計算結(jié)果作為參考結(jié)果。根據(jù)式（15）可得單個關(guān)節(jié)對機器人末端定位誤差，將x軸方向的誤差作為功能函數(shù)，其中式（26）小于0時定義為失效。

式中，x=y=z=200 mm，θ=π/3，r為閾值。為了方便理解，考慮單關(guān)節(jié)影響并以x方向為例，采用上述三種方法計算不同閾值下的機器人末端定位精度失效概率和可靠性指標(biāo)，其中閾值r從0.1 mm變化到1.4 mm，計算結(jié)果如表3所示。表中失效概率表示式（26）x方向定位誤差小于等于閾值r的概率，可靠性指標(biāo)與失效概率在數(shù)學(xué)上存在如下對應(yīng)關(guān)系[23]：

Pf=Φ（-β）=1-Φ（β）， ???（27）

式中，Pf表示失效概率，β表示可靠性指標(biāo)，Φ（·）表示標(biāo)準(zhǔn)正態(tài)分布的累計分布函數(shù)。由式（27）可見，當(dāng)失效概率大于0.5時，可靠性指標(biāo)為負(fù)數(shù)。為了更直觀地比較三種方法，將表3中的數(shù)據(jù)繪制成曲線如圖7所示。

圖7中橫坐標(biāo)表示閾值，縱坐標(biāo)表示功能函數(shù)的失效概率。MCS與考慮約束的MCS結(jié)果差距很大，新分布的MCS與考慮約束的MCS的結(jié)果更為接近，說明新分布能夠包含約束方程的信息，因此在分析關(guān)節(jié)間隙對機器人末端精度可靠性的影響時，關(guān)節(jié)間隙中各個參數(shù)應(yīng)符合本節(jié)所采用的分布。

3工程實例

3.1幕墻安裝機器人誤差模型

圖8和圖9分別為高空幕墻安裝機器人的實物圖[24]和結(jié)構(gòu)簡圖，該建筑機器人在構(gòu)型上包含兩個平行四邊形機構(gòu)。以此類建筑機器人為例，采用提出的方法對該機器人末端單點定位精度進(jìn)行分析。首先，分析D點和H點處被動關(guān)節(jié)繞轉(zhuǎn)動副軸線的轉(zhuǎn)動誤差，具體流程見2.2節(jié)，結(jié)果如式（25）所示。設(shè)BC長度為D1，DG長度為D2，則D點和H點繞轉(zhuǎn)動副軸線的轉(zhuǎn)動誤差為

根據(jù)銷軸與桿件是否固連，鉸鏈連接可分為兩種[11]：第一種為銷軸固連在桿件上，如圖10（a）所示，兩個桿件之間含有一個關(guān)節(jié)間隙；第二種為銷軸不連接在桿件上，如圖10（b）所示，此時鉸鏈連接處含有兩個關(guān)節(jié)間隙。高空幕墻安裝機器人除了D點的關(guān)節(jié)采用圖10（b）所示的連接方式，其余關(guān)節(jié)都為圖10（a）所示的連接方式。當(dāng)已知被動關(guān)節(jié)繞轉(zhuǎn)動副軸線的轉(zhuǎn)動誤差后，便可將機器人看作含有7個關(guān)節(jié)的串聯(lián)機器人，具體坐標(biāo)系建模方式如圖11所示。在每個關(guān)節(jié)建立兩個坐標(biāo)系gi和gi0，其中g(shù)i為關(guān)節(jié)處的基礎(chǔ)坐標(biāo)系，gi0為關(guān)節(jié)間隙模型坐標(biāo)系也稱局部坐標(biāo)系。由于高空幕墻安裝機器人含有兩個平行四邊形機構(gòu)，因此連桿DE會始終保持水平狀態(tài)，第三軸角度θ4由θ2和θ3耦合而成，進(jìn)一步分析可得θ4=-（θ2+θ3）。高空幕墻安裝機器人D-H參數(shù)如表4所示。

如圖11所示，關(guān)節(jié)間隙引起的高空幕墻安裝機器人末端定位誤差可視為由8個關(guān)節(jié)間隙（D處含有兩個關(guān)節(jié)間隙）引起誤差，通過2.1節(jié)和2.2節(jié)建模方法可得最終誤差如下

δE=M1·σ10+M2·σ20+M3σ310+M3·σ320+M4·σ40+M5·σ50+M6·σ60+M7·σ70， ???（30）

式中，Mi為第i個關(guān)節(jié)處關(guān)節(jié)間隙機器人末端定位精度的影響矩陣；σi0表示第i個關(guān)節(jié)的模型參數(shù)。其中關(guān)節(jié)3處對應(yīng)圖9中D點的位置，為圖10（b）的鉸鏈接觸類型，在求解關(guān)節(jié)3處間隙對機器人末端定位精度的影響時需考慮兩個關(guān)節(jié)間隙，因此σ310表示關(guān)節(jié)3處第一個關(guān)節(jié)間隙模型在關(guān)節(jié)3處引起的誤差，σ320表示第二個關(guān)節(jié)間隙模型在關(guān)節(jié)3處引起的誤差。

3.2基于降維積分的可靠性分析方法

為準(zhǔn)確評估關(guān)節(jié)間隙對機器人末端精度的影響，考慮關(guān)節(jié)間隙處全方向誤差，MCS需要大量計算，無法滿足實際工程需求。基于降維積分方法的可靠性分析方法能夠在保證精度的同時減少功能函數(shù)的調(diào)用次數(shù)。其中采用雙變量降維方法準(zhǔn)確求解功能函數(shù)的前四階矩；然后采用鞍點近似方法構(gòu)建機器人誤差的概率密度函數(shù)（probability density function， PDF）進(jìn)而分析可靠性。

3.2.1雙變量降維法

由于機器人關(guān)節(jié)較多，功能函數(shù)公式復(fù)雜，求解功能函數(shù)的前四階矩容易造成“維數(shù)災(zāi)難”，在保證精度的同時需要通過降維方法避免直接求解高維積分。假定結(jié)構(gòu)的功能函數(shù)為[25]

雙變量降維（bivariate dimension-reduction method， BDRM）需要將隨機變量轉(zhuǎn)換特定分布的正態(tài)變量，輸入隨機變量Xi（i=1，2，…，n）轉(zhuǎn)換到Ui～N（0，0.5）轉(zhuǎn)換公式為

利用高斯-埃爾米特積分求解式（38）中一維積分和二維積分，得到目標(biāo)函數(shù)的整數(shù)原點矩。

3.2.2鞍點近似

獲得功能函數(shù)的前四階矩后，可采用鞍點近似（saddle point approximation， SPA）方法擬合功能函數(shù)響應(yīng)的概率分布。根據(jù)SPA方法，Y的累積量生成函數(shù)（cumulant generating function， CGF）定義為[25]

式中，sgn（·）表示符號函數(shù)。

3.3定位精度可靠性分析結(jié)果

關(guān)節(jié)間隙引起的機器人定位誤差由式（30）所示，設(shè)轉(zhuǎn)角θ1=0、θ2=π/3、θ3=2π/3、θ5=0、θ6=4π/9、θ7=0。設(shè)機器人x、y和z軸方向的定位誤差分別為ex、ey和ez。當(dāng)定位誤差小于一定閾值后表示機器人定位失效。采用考慮約束的MCS、新分布的MCS、BDRM和單變量降維（univariate dimension-reduction method，UDRM）四種方法計算ex、ey和ez的前四階矩分別如表5～7示。

通過表5～7可以看出BDRM前四階矩與考慮約束的MCS結(jié)果十分接近，而UDRM中第四階矩誤差較大。這是由于UDRM不能很好解決誤差模型中參數(shù)之間相互耦合問題。因此本文采用BDRM準(zhǔn)確求解前四階矩。

如圖12和圖13所示，已知功能函數(shù)的前四階矩，可通過鞍點近似方法擬合定位誤差概率密度函數(shù)并求解不同閾值下的定位精度可靠度，將擬合曲線與考慮約束的MCS的擬合曲線進(jìn)行對比。

考慮約束的MCS功能函數(shù)調(diào)用次數(shù)為106，雙變量降維方法和鞍點近似方法對ex、ey和ez三個功能函數(shù)的調(diào)用次數(shù)分別為1 459次，3 043次和2 889次。通過圖12和圖13可知，雙變量降維方法和鞍點近似方法相比于MCS調(diào)用功能函數(shù)次數(shù)較少，并且能準(zhǔn)確分析由空間關(guān)節(jié)間隙引起的混聯(lián)機器人定位精度可靠性。

4結(jié)論

針對空間關(guān)節(jié)間隙對混聯(lián)機器人定位精度的影響，本文提出了一種混聯(lián)機器人誤差建模方法，并對關(guān)節(jié)模型參數(shù)進(jìn)行了不確定性度量，最后采用雙變量降維方法和鞍點近似方法分析定位精度可靠性。

1） 研究空間關(guān)節(jié)間隙的隨機不確定性對含有閉鏈機構(gòu)混聯(lián)機器人定位精度的影響規(guī)律。提出了一種基于旋量理論的混聯(lián)機器人定位精度誤差模型，該模型能夠合理分析空間關(guān)節(jié)間隙不確定性對機器人末端定位精度的影響。

2） 考慮空間轉(zhuǎn)動關(guān)節(jié)間隙引起的誤差需滿足一定約束條件，對間隙模型參數(shù)的不確定性進(jìn)行度量，獲得混聯(lián)機器人考慮關(guān)節(jié)間隙的定位精度可靠性模型。

3） 采用雙變量降維方法計算混聯(lián)機器人定位誤差的統(tǒng)計矩，運用鞍點近似方法擬合其定位誤差的概率密度函數(shù)，分析機器人x軸、y軸和z軸的定位精度可靠性。其中MCS方法需要調(diào)用功能函數(shù)106次，本文方法計算機器人x軸、y軸和z軸的定位精度可靠性分別需要1 459次，3 043次和2 889次。

此外，本文方法可以與D-H參數(shù)法和旋量理論等機器人運動學(xué)分析方法相結(jié)合，形成更為系統(tǒng)性的可靠性分析方法，用以評估不同誤差來源對機器人定位精度的綜合影響。

參考文獻(xiàn)

[1] ZHANG D，HAN X.Kinematic reliability analysis of robotic manipulator[J].Journal of Mechanical Design，2020，142（4）： 044502.

[2] 李文龍，謝核，尹周平，等.機器人加工幾何誤差建模研究：Ⅰ空間運動鏈與誤差傳遞[J].機械工程學(xué)報，2021，57（7）： 154-168.

LI W L，XIE H，YIN Z P，et al.A study on modeling of geometric errors in robot machining：Ⅰ spatial motion chain and error transfer[J].Journal of Mechanical Engineering，2021，57（7）： 154-168.

[3] 梁云飛，張德權(quán)，彭周源.一種高效的概率-證據(jù)混合工業(yè)機器人定位精度可靠性分析方法[J].燕山大學(xué)學(xué)報，2022，46（4）： 309-318.

LIANG Y F，ZHANG D Q，PENG Z Y.An efficient reliability analysis method for positioning accuracy of industrial robot through probability and evidence theory [J].Journal of Yanshan University，2022，46（4）： 309-318.

[4] ZHANG D，PENG Z，NING G，et al.Positioning accuracy reliability of industrial robots through probability and evidence theories[J].Journal of Mechanical Design，2021，143（1）： 011704.

[5] ZHANG J，DU X.Time-dependent reliability analysis for function generation mechanisms with random joint clearances[J].Mechanism Machine Theory，2015，92： 184-199.

[6] TING K L，HSU K L，YU Z，et al.Clearance-induced output position uncertainty of planar linkages with revolute and prismatic joints[J].Mechanism Machine Theory，2017，111： 66-75.

[7] 侯雨雷，趙劉見，齊曉鳳，等.一種含間隙的柔性并聯(lián)機構(gòu)動力學(xué)仿真[J].燕山大學(xué)學(xué)報，2019，43（6）： 485-496.

HOU Y L，ZHAO L J，QI X F，et al.Dynamic simulation of flexible parallel mechanism by considering clearance[J].Journal of Yanshan University，2019，43（6）： 485-496.

[8] BRIOT S，BONEV I A.Accuracy analysis of 3-dof planar parallel robots[J].Mechanism Machine Theory，2008，43（4）： 445-458.

[9] CHEN X，GAO S.Dynamic accuracy reliability modeling and analysis of planar multi-link mechanism with revolute clearances[J].European Journal of Mechanics-A/Solids，2021，90： 104317.

[10] ZHAN Z，ZHANG X，JIAN Z，et al.Error modelling and motion reliability analysis of a planar parallel manipulator with multiple uncertainties[J].Mechanism Machine Theory，2018，124： 55-72.

[11] 趙強強，洪軍，郭俊康，等.多環(huán)閉鏈機構(gòu)偏差傳遞分析及幾何精度建模[J].機械工程學(xué)報，2018，54（21）： 156-165.

ZHAO Q Q，HONG J，GUO J K，et al.Analysis of deviation transfer and geometric accuracy modeling of multi-loop closed chain mechanism[J].Journal of Mechanical Engineering，2018，54（21）： 156-165.

[12] ZHAO Q，GUO J，HONG J.Closed-form error space calculation for parallel/hybrid manipulators considering joint clearance，input uncertainty，and manufacturing imperfection[J].Mechanism Machine Theory，2019，142： 103608.

[13] 侯雨雷，張國興，張繼永，等.3PSS/S并聯(lián)機構(gòu)運動誤差預(yù)估與補償[J].燕山大學(xué)學(xué)報，2020，44（1）： 11-17.

HOU Y L，ZHANG G X，ZHANG J Y，et al.Prediction and compensation of motion error of 3PSS/S type parallel mechanism[J].Journal of Yanshan University，2020，44（1）： 11-17.

[14] FRISOLI A，SOLAZZI M，PELLEGRINETTI D，et al.A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances[J].Mechanism Machine Theory，2011，46（12）： 1929-1949.

[15] WU G，BAI S，KEPLER J A，et al.Error modeling and experimental validation of a planar 3-ppr parallel manipulator with joint clearances[J].Journal of Mechanisms Robotics，2012，4（4）： 041008.

[16] MENG J，LI Z.A general approach for accuracy analysis of parallel manipulators with joint clearance[C]// 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems，Edmonton，Canada，2005： 2468-2473.

[17] PAC M R，POPA D O.Interval analysis of kinematic errors in serial manipulators using product of exponentials formula[J].IEEE Transactions on Automation Science Engineering，2013，10（3）： 525-535.

[18] 張艷芳，張艷林.一種機械元件失效概率計算的方法[J].機械強度，2020，42（5）： 1125-1129.

ZHANG Y F，ZHANG Y L.A method for calculating failure probability of mechanical components [J].Journal of Mechanical Strength，2020，42（5）： 1125-1129.

[19] WU J，ZHANG D，LIU J，et al.A moment approach to positioning accuracy reliability analysis for industrial robots[J].IEEE Transactions on Reliability，2019，69（2）： 699-714.

[20] 王明良.面向3C拾放應(yīng)用的碼垛機器人機構(gòu)優(yōu)化設(shè)計研究[D].哈爾濱： 哈爾濱工業(yè)大學(xué)，2018.

WANG M L.Research on the optimal design of palletizing robot mechanism for 3C pick-and-place applications[D].Harbin： Harbin Institute of Technology，2018.

[21] VENANZI S，PARENTI-CASTELLI V.A new technique for clearance influence analysis in spatial mechanisms[J].Journal of Mechanical Design，2005，127（3）： 446-455.

[22] 陳慶誠，朱世強，王宣銀，等.基于旋量理論的串聯(lián)機器人逆解子問題求解算法[J].浙江大學(xué)學(xué)報（工學(xué)版），2014，48（1）： 8-14.

CHEN Q C，ZHU S Q，WANG X Y，et al.Inverse subproblem solving algorithm for series robot based on spinor theory [J].Journal of Zhejiang University （Engineering Science），2014，48（1）： 8-14.

[23] 張明.結(jié)構(gòu)可靠度分析——方法與程序[M].北京： 科學(xué)出版社，2008.

ZHANG M.Structural reliability analysis-methods and procedures [M].Beijing： Science Press，2008.

[24] 田飛.高空幕墻安裝機器人機械系統(tǒng)研究[D].天津： 河北工業(yè)大學(xué)，2015.

TIAN F.Research on robotic mechanical system for high-altitude curtain wall installation[D].Tianjin： Hebei University of Technology，2015.

[25] HUANG B，DU X.Uncertainty analysis by dimension reduction integration and saddlepoint approximations[J].Journal of Mechanical Design，2006，128（1）： 26-33.

Joint clearance error modeling and positioning

accuracy reliability analysis of hybrid robot

GUO Tianyu1， 2， ZHANG Dequan1， 2， WU Jinhui1， 2， ZHOU Pengfei1， 2， MENG Yuan1， 2

（1.State Key Laboratory of Reliability and Intelligence of Electrical Equipment，Hebei University of Technology，Tianjin 300401，China;

2.School of Mechanical Engineering，Hebei University of Technology，Tianjin 300401，China）

Abstract：The reliability of robot end positioning accuracy is an important index to measure its accuracy performance.Joint clearance is one of the main factors affecting robot positioning accuracy，and establishing an accurate robot positioning accuracy error model is a prerequisite for reliability analysis.In order to investigate the influence of the random uncertainty of the spatial joint clearance on the positioning error of a hybrid robot containing a closed chain mechanism.A hybrid robot positioning accuracy error model considering joint gaps is proposed using spinor theory and the D-H parameter method.To quantify the uncertainty of the gap model parameters according to the constraints of the joint gap model parameters and to establish a reliability model for the positioning accuracy of the hybrid robot.The bivariate dimensionality reduction method and saddlepoint approximation method are used to fit the probability density function of the robot′s uni-coordinate positioning error to achieve hybrid robot positioning accuracy reliability analysis.The accuracy and engineering applicability of the proposed model are verified by taking a construction robot containing a parallelogram closed-chain mechanism as an example，and the results show that the proposed method greatly improves the efficiency compared with the traditional Monte Carlo method.

Keywords： hybrid robot;positioning accuracy;joint clearance;uncertainty;reliability analysis