混合粒子群算法計算數控加工逼近誤差研究*

李鵬飛,劉 威,張子煜,康 嘉,張嘉萍

(蘇州科技大學機械工程學院,蘇州 215000)

0 引言

數控加工是高精度復雜曲面的最重要加工手段,精加工使用的刀軌直接決定最終的加工精度。逼近誤差是指刀具在進給方向上從一個刀位點運動到下一個刀位點形成的包絡面與刀觸點軌跡線之間的最大誤差。相鄰刀觸點、刀位點的距離(即步長)越大,逼近誤差越大。步長規劃方法主要有等參數法、等距法、步長篩選法和等誤差步長法[1-2]。目前計算逼近誤差一般采用幾何迭代法[3-4],現有算法模式幾乎無法再提高計算效率,當需要大量逼近誤差計算的高精度刀軌(如等誤差刀軌)生成時,逼近誤差計算時間難以減少。逼近誤差計算效率低已成為制約高質量刀軌廣泛應用的主要瓶頸之一。

逼近誤差計算的實質是在刀觸點軌跡線上搜索一刀觸點,此刀觸點到刀位點連線的距離為最值,此最值可確定逼近誤差值。智能優化算法是常用的高效率的最值計算方法,它們是通過對生物群體協同搜索機制和物理原理驅動下的變化現象抽象、提煉出的優化算法,在全局尋優的精度和效率上比傳統的迭代法優勢明顯[5],理論上能夠用于在刀觸點軌跡線上搜索與刀位點連線的距離為最值的點。

常見的智能算法有粒子群優化算法(particle swarm optimization,PSO)[6]、遺傳算法(genetic algorithm,GA)[7]、模擬退火算法(simulated annealing,SA)[8]、引力搜索算法(gravitational search algorithm,GSA)[9]等。PSO算法模擬鳥群或蜂群的覓食行為進行最優解搜索。GA算法是一種基于進化論的優化算法,其核心思想是通過模擬自然界中的遺傳機制,逐步優化問題的解決方案。GA算法因為遺傳算子交叉變異操作使其具有較強的全局搜索能力,但收斂速度慢。

作為應用最廣泛的智能算法之一,PSO因計算高效,被廣泛應用于多個領域[10]。但標準PSO易過早收斂、陷入局部最優[11]。為此,SHI等[12]提出了帶約束因子的PSO算法,以提高算法靈活性和收斂速度。EBERHART、SHI等[13-15]則對慣性權重的變化分別提出了線性遞減、隨機慣性、非線性遞減的優化策略,以保持局部最優和全局最優之間的平衡。PENG等[16]提出一種跟隨非線性慣性權重系數變化的動態學習因子,以提高算法的全局搜索能力和局部搜索精度。SHI、GONG等[7-9]分別提出GA算法、SA算法、GSA算法與PSO算法相結合的方法。

受PSO算法、逼近誤差計算過程原理相似和上述研究成果啟發,綜合PSO算法與GA算法兩種算法的優點,本文首先結合逼近誤差特點對標準PSO算法種群初始化、慣性權重因子、學習因子進行優化,然后將GA算法中的交叉變異策略引入優化后的PSO算法中,構建出混合PSO算法,最終實現逼近誤差的高效、高精度計算。

1 逼近誤差計算模型構造

1.1 逼近誤差幾何原理

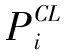
(1)

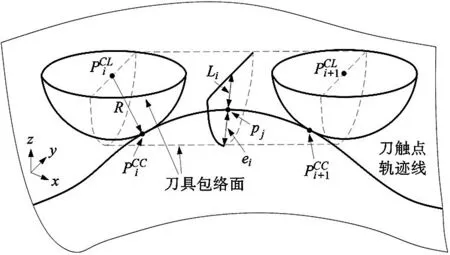
圖1 逼近誤差ei示意圖

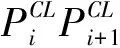
1.2 建立刀觸點軌跡線區間與粒子搜索區間的映射

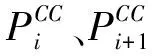
(2)

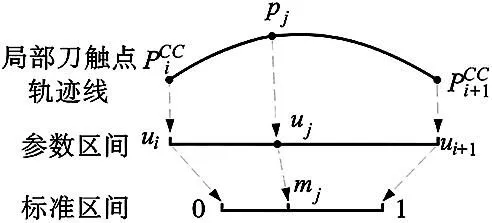
圖2 刀觸點Pj映射到標準區間示意圖

1.3 建立逼近誤差計算的適應度函數

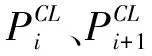
步驟1:運用式(3)計算出粒子mj所對應的刀觸點的參數值uj,代入式(4)計算出參數值uj在刀觸點軌跡線CC上對應的點pj;

uj=mjui+(1-mj)ui+1

(3)

pj=CC(uj)

(4)

步驟2:運用式(1)計算出刀觸點到刀位點連線之間的距離Lj;

步驟3:運用式(5)計算出粒子mj的適應度值f(j)。

f(j)=|R-Lj|

(5)

2 混合粒子群算法

為了提高計算效率,結合逼近誤差的幾何原理,本節基于標準PSO算法提出混合PSO算法:引入Tent映射的種群初始化,設計基于sigmoid函數的非線性慣性權重系數,運用非線性控制方法學習因子,以改進標準PSO算法的效率;引入GA算法中的交叉變異算子,提高算法的全局搜索能力,從而建立適用于逼近誤差計算的混合PSO算法。

2.1 構建標準粒子群算法

標準PSO算法計算過程中,每個粒子都能夠由適應度函數計算出適應度值,記錄個體的適應度極值pbest與群體極值gbest,以此驅動粒子在迭代計算中更新位置和速度,最終計算出滿足精度要求的理論最優解。

將標準PSO算法用于在刀觸點軌跡線上搜索一個到刀位點連線的距離為最值刀觸點,刀觸點粒子的速度和位置的更新如式(6)所示。

(6)

式中:xi(k)、vi(k)分別為第i個粒子在第k次迭代時速度和位置,w為慣性權重因子,c1、c2分別為個體、社會學習因子,r1、r2為(0,1)之間相互獨立的隨機數。隨著迭代次數的增加,所獲得的極值逐漸逼近理論解,一般以迭代次數上限或極值變化量作為終止條件結束算法。

2.2 基于Tent映射的種群初始化

在PSO算法中,初始化粒子的位置對算法的收斂速度和性能有著重要的影響。作為一種典型的混沌序列映射函數,Tent映射生成的混沌序列隨機性好,具有簡單易實現、計算速度快等優點[17],將Tent映射引入PSO算法能夠可以有效地擴展搜索空間,提高全局搜索能力。

由于精加工的相鄰刀觸點之間的局部刀觸點軌跡線長度較小,曲率變化不大,因此逼近誤差理論刀觸點位置基本分布在搜索區間的中間位置附近。為此,提出使用Tent映射生成[0,1]之間隨機數,并通過線性變換將這些隨機數映射到中間區間[0.25,0.75]上,作為PSO算法初始粒子的位置。具體實現步驟為:

步驟1:生成[0,1]之間的一個隨機數,作為初始值x0;

步驟2:通過Tent映射公式計算下一個值,如式(7)所示;

(7)

步驟3:將xi的值線性映射到[0.25,0.75]之間,如式(8)所示;

(8)

2.3 慣性權重優化

慣性權重w表示粒子繼承先前速度的多少,PSO算法的初期一般需要較大的慣性權重因子以獲得較強的全局搜索能力,并隨著迭代次數增加遞減,從而加快粒子收斂。為了提高逼近誤差計算效率,鑒于非線性動態慣性權重的綜合性能優于線性[18],本文利用sigmoid函數曲線在區間[-6,6]內的前、中、后段上升速度由慢到快再到慢的非線性特點,提出將PSO算法的迭代次數映射到此區間,獲得如式(9)所示的慣性權重函數,此函數能夠在搜索初期、中期、后期分別獲得較慢、較快、較慢的慣性權重下降速度,從而使粒子的全局搜索能力在初期時較強,隨后中期近似線性遞減,局部搜索能力逐漸增強,后期變化率再次減小,保證較強的局部搜索能力。

(9)

式中:k為迭代次數,wmax、wmin為慣性權重系數最大、最小值。

2.4 非線性學習因子設置

PSO算法的學習因子c1和c2分別調節個體學習能力和群體學習能力。當c1>c2時,粒子的運動更偏向個體最優方向,反之則更偏向群體最優方向。c1取值過大時,會導致過多刀觸點粒子聚集于局部刀觸點軌跡線,影響全局尋優效果;c2取值過小時,刀觸點粒子會過早收斂局部最優。

鑒于刀觸點軌跡線的凹凸性易使計算逼近誤差時陷入局部最優,合適的尋優策略是:在迭代初期,由于位置不確定性,粒子應注重自我認知,側重個體最優解進行全局搜索;在迭代后期,粒子較為接近最優位置,應注重群體認識,側重群體最優解鄰域的局部搜索。為此,本文在文獻[9]學習因子變化策略的基礎上,提出了基于迭代次數的學習因子非線性變化方法,使得c1、c2隨著迭代次數k的增加而分別減小、增大,如式(10)所示。

(10)

式中:c1max、c1min、c2max和c2min分別為個體、群體學習因子的最大、最小值。

2.5 基于粒子交叉變異的算法優化

為了進一步改善PSO算法容易陷入局部最優解的問題,引入GA算法的交叉變異策略提高刀觸點粒子的全局搜索能力。

交叉方面,將刀觸點粒子以固定交叉概率放入交叉池中,在雜交池中隨機挑選出兩兩相互獨立刀觸點粒子進行交叉,根據兩刀觸點粒子的位置平均值計算出的交叉權重確認交叉點,直到雜交池中所有粒子完成交叉操作。交叉操作有助于交叉后的刀觸點粒子繼承交叉前粒子的優勢并保持種群的多樣性,交叉后粒子位置由兩交叉粒子的位置加權計算,新個體的位置公式如式(11)所示。速度公式如式(12)所示。

(11)

(12)

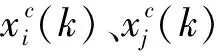
變異方面,在每次進化中,為了彌補了隨機突變的不準確性,提出對交叉后的新粒子群體根據固定的變異概率pm選取粒子進行變異,有效地增加了種群的多樣性。對交叉后的刀觸點粒子計算適應度值,進行降序排列,對適應度值較小(即距離理論逼近誤差刀觸點位置較遠)的刀觸點粒子進行變異操作,將(0,1)之間隨機數作為變異后粒子的位置,使它們具有一定概率跳動到理論逼近誤差刀觸點位置附近。刀觸點粒子位置公式如式(13)所示。

(13)

2.6 混合粒子群算法總體流程

基于2.1～2.5節提出的PSO算法構建和優化方法,可規劃出混合PSO算法計算逼近誤差的整體流程,具體步驟如下,流程如圖3所示。

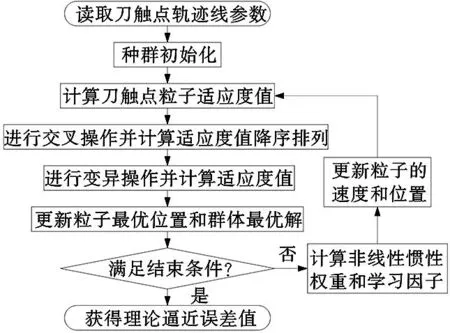
圖3 逼近誤差計算流程圖

步驟1:將搜索區間[ui,ui+1]映射到[0,1],設置種群規模N和速度閾值vmax、vmin,交叉概率pc,變異概率pm,設置最大迭代次數kmax或計算精度作為終止條件,初始化速度和位置;

步驟2:計算全部粒子的適應度值;

步驟3:對刀觸點粒子以交叉概率pc進行交叉操作,對交叉操作后的刀觸點粒子計算適應度值并進行降序排列;

步驟4:以變異概率pm選擇交叉操作后適應度值最小的刀觸點粒子的粒子進行變異操作;

步驟5:計算變異操作后粒子適應度值并記錄pbest與gbest;

步驟6:判斷是否滿足收斂條件(如滿足計算精度或達到最大迭代次數),如果滿足轉向步驟7;否則以式(9)改變慣性權重w,根據式(10)改變學習因子c1、c2。根據式(6)更新粒子的速度和位置,轉向步驟2繼續迭代;

步驟7:輸出當前最優粒子位置和適應度值,作為理論逼近誤差位置和逼近誤差值,算法終止。

3 算法實現與驗證

3.1 算法實現

算法的實現需要對種群規模N、最大迭代次數kmax、最大速度vmax與最小速度vmin、慣性權重w、學習因子c1和c2、交叉概率pc、變異概率pm進行設置。

較小的種群規模N與最大迭代次數kmax可能會導致算法陷入局部最優解,而較大的種群規模與最大迭代次數可以提高算法的全局搜索能力,但增加了算法的計算量,參考文獻[19]進行測試,設置種群規模N為50,最大迭代次數kmax為100。

最大速度和最小速度的取值范圍通常在搜索空間的范圍內,并且被設置為搜索空間范圍的一定比例。通過測試、比較不同取值,選取最大速度和最小速度設置為搜索空間范圍的20%與5%,即速度閾值vmax與vmin為0.2與0.05時算法收斂速度較好。

慣性權重最大最小值wmax和wmin的取值也影響算法的收斂速度,然而取值并無明確的理論依據,多采用實驗法選值,常將其設置在0.4～0.9之間[19]。算法選用了多組數值進行測試,當wmax=0.9、wmin=0.4時,性能提高明顯,代入式(9)獲得慣性權重w計算式,w隨迭代次數k的變化如圖4所示。

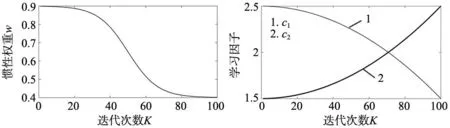
圖4 慣性權重變化圖

與慣性權重類似,常將個體、群體學習因子設置為固定值2[19]。本文結合優化后慣性權重的變化趨勢,在選用了多組數值組合進行了測試后,確定當c1max=2.5、c1min=1.5、c2max=2.5、c2min=1.5時,學習因子變化如圖5所示,滿足了前中期加強粒子運動遍歷性、全局搜索能力和后期加強局部搜索能力的要求。

交叉和變異概率的設置與粒子搜索區間復雜度有關,如果解空間較大且復雜,較高的交叉和變異概率可以更好地探索潛在解;相反,如果解空間較小或具有明顯的最優解,較低的概率可能足夠。參照文獻[7],算法選用多組數值進行測試,交叉概率pc和變異概率pm分別為0.6和0.05時,算法有較好的收斂速度。

完成上述數值選取后,在課題組自主開發的CAM軟件上完成了所有算法的程序開發,實現了逼近誤差計算功能。

3.2 算法驗證

以圖6a中的曲面為例生成刀軌,曲面包圍盒尺寸為190 mm×150 mm×45 mm,選擇直徑10 mm的球頭刀,刀軌行數為150,使用等誤差步長法生成刀軌,逼近誤差允許區間為[9 μm,10 μm],計算精度為0.1 μm。分別采用幾何迭代算法、標準PSO算法和本文提出的混合PSO算法計算逼近誤差,進而生成等誤差刀軌。生成的刀軌如圖6b所示,仿真圖如圖6c所示,運行環境為Intel i5-13400、16 G RAM的計算機,3種算法所消耗的時間如表1所示,本文算法比幾何迭代算法的計算時間減少了18%以上,比標準PSO優化算法的計算時間減少了8%以上,驗證了算法的高效率。

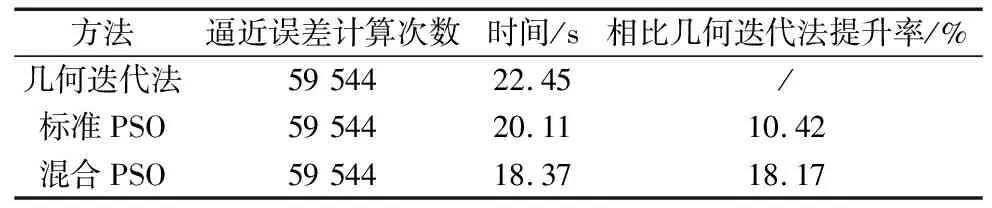
表1 等誤差刀軌的計算時間

(a) 曲面示意圖 (b) 等誤差刀軌 (c) 等誤差刀軌加工仿真圖

4 結論

為了提高數控加工中逼近誤差的計算效率,本文研究了基于混合PSO算法的逼近誤差計算方法。將刀觸點設置為粒子,將刀觸點軌跡線上搜索范圍映射到標準區間[0,1],提出了適應度函數;結合逼近誤差特點引入Tent映射初始化種群,優化了慣性權重因子和學習因子的變化策略并引入了GA算法的交叉變異操作。測試結果表明,所提出的混合PSO算法耗時更短。在未來的研究中,可進一步在結構、參數優化等方面改進算法,或探索其它類型的智能算法,以進一步提高逼近誤差的計算效率。