面向傳動性能的分體式RV減速器結構優化*
楊晨昊,王金棟,李 澳,唐雷雨
(西南交通大學機械工程學院,成都 610031)
0 引言
RV減速器作為精密傳動裝置的一種,由行星輪傳動和擺線針輪傳動組成,具有大傳動比、高負載、高傳動精度等優勢,被廣泛運用在工業機器人的生產加工中[1]。國產RV減速器起步較晚,在技術層面與國外廠商還有一定差距[2]。作為精密傳動的一種,復雜的修形方法、嚴苛的公差要求是制約國產RV減速器發展的原因[3]。
在提高RV減速器傳動性能的問題上,國內外學者開展了諸多研究。為提高RV減速器的傳動精度與可靠性,于明以減速器整體體積最小化為設計目標,將關鍵零部件的主要尺寸作為設計變量的同時保持傳動比與輸出功率不變完成RV減速器的結構設計[4]。張誠針對RV減速器傳動精度問題,為減小回差對傳動過程的影響,將減速器的幾何回差作為研究目標,各零部件的主要公差項作為設計變量建立優化設計模型[5]。WANG等[6]以體積和效率作為優化目標,使用遺傳算法對單級擺線減速器,進行多目標優化設計。由于常見RV減速器減速比固定不能適應復雜工況,黃津晶提出了一種傳動精度高、結構緊湊且力學性能良好,能夠實現傳動比可變的變傳動比RV減速器[7]。針對RV減速器工作過程中振動噪聲的問題,CHEN等[8]通過建立集中參數的動力學模型分析陀螺效應與關鍵幾何尺寸對RV減速器自由振動特性的影響。王新春[9]在對擺線輪齒廓傳統修形方法深入研究的基礎上,提出了一種基于擺線輪齒廓二次包絡理論的等移距組合修形量計算的新方法,大大提高了擺線輪齒廓修形量的計算精度。HUANG等[10]通過建立非線性約束優化模型對RV減速器軸承進行優化設計,以提高RV減速器工作壽命,避免發生疲勞失效。傳動效率是限制現代RV減速器發展的重要原因,WANG等[11]通過推導一種RV減速器傳動效率的計算方法,建立體積-效率目標函數,實現RV減速器高功率密度設計。LIU等[12]分析了同軸度誤差對RV減速器的影響,設計了一臺高精度檢測裝置,建立RV減速器同軸度-幾何回差模型,揭示了同軸度對幾何回差的影響規律。宿月文等[13]對RV減速器傳動誤差進行建模,對減速器傳動誤差影響小的尺寸參數的誤差等級進行修正,在保證傳動精度的同時有效降低了減速器的加工誤差。丁國龍等[14]建立了RV減速器傳動誤差與固有頻率的數學模型,揭示了RV減速器模態對傳動誤差的影響規律。
通過上述分析可以看出目前研究人員關注的重點主要集中在傳動構件結構優化、擺線輪齒廓修形,通過以上方式提高機構的可靠性和傳動精度。伴隨著傳動精度的提高,擺線輪齒廓曲線也愈加復雜,減速器尺寸參數的精度要求也逐漸嚴苛,致使關鍵零部件的加工工藝復雜、加工難度大。因此在保證傳動精度的同時,如何降低RV減速器加工難度,提高傳動效率是亟需研究的關鍵問題。
本文在分析RV減速器工作原理的基礎上,提出一種分體式RV減速器設計方法,并進一步推導結構尺寸與系統受力間的關系,通過遺傳算法對減速器各項尺寸進行優化實現面向性能的RV減速器結構設計。并利用虛擬樣機仿真對設計方案的合理性進行驗證。
1 RV擺線輪結構與減速器總體設計
1.1 擺線輪結構分析
如圖1a所示,標準擺線輪的齒廓是一條連續的擺線,加工方法為數控銑削、冷擠壓、成形磨削工藝等。
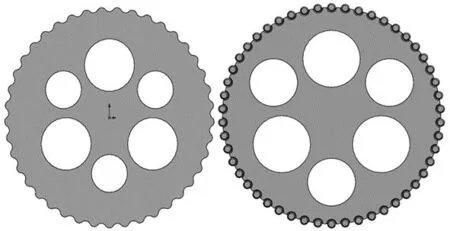
(a) 標準擺線輪 (b) 分體式擺線輪
如圖1b所示,連續齒廓離散后,擺線輪輪齒被圓柱滾針替代,與擺線輪齒相比滾針的外形輪廓更簡單,加工方法為車削與鉆孔。
1.2 減速器總體設計
1.2.1 減速器傳動比分配及齒輪基本參數的計算
RV減速器是一種大傳動比、高效率傳動機構,針齒殼固定,太陽輪輸入,行星架輸出時,傳動比為:
(1)
式中:i為傳動比,z1為太陽輪齒數,z2為行星輪齒數,z4為外殼針齒齒數。
在RV減速器工作過程中,摩擦損失是影響傳動效率的主要原因,功率從輸入軸經齒輪嚙合、軸承轉動與針齒嚙合到達輸出軸。功率損失可以劃分為齒輪嚙合摩擦損失和滾動軸承摩擦損失,因此RV傳動的傳動效率為:
η=η16ηB
(2)
式中:ηB為軸承總效率且ηB=ηB1ηB2ηB3,ηB2為轉臂軸承效率,取0.99;ηB2為曲柄支撐軸承效率,取0.99;ηB3為行星架支撐軸承效率,取0.99;η16為RV嚙合效率與減速器傳動比相關,因此:
(3)
通過對傳動效率公式分析可知,漸開線齒輪傳動的傳動比對傳動效率有較大影響,在選擇傳動方案時需要對傳動比進行控制。
通過對RV減速器運動封閉的特點以及兩級傳動機構分析,可以得到減速器的基本幾何約束條件:
(1)擺線針輪機構作為差齒傳動的一種,大傳動比會影響減速器的整體體積與重量,導致擺線輪齒廓負載,提高零部件的加工難度。進而影響RV傳動的傳動精度與承載能力,為保證其傳動比不會過大,行星減速機構的傳動比滿足:u=z2/z1>1.5。
(2)在行星齒輪傳動過程中,為保證各曲軸傳動過程中的同步性,太陽輪齒數是行星輪數量的整數倍。在漸開線行星傳動機構中,為保證齒輪不發生根切且保證輪齒的磨損,根據變位系數、齒頂厚以及齒數之間的關系,中心輪齒數z1的選取范圍為[9,20][15]。
(3)為保證傳動過程中,行星輪的齒頂圓間不發生干涉,行星輪齒頂圓應滿足:da<2asinπ/n。
(4)在傳動過程中輪齒應不發生膠合或折斷,太陽輪模數m應滿足彎曲疲勞強度校核,分度圓應滿足接觸疲勞強度校核。
綜合上述約束條件,確定減速器的主要結構參數,計算流程圖如圖2所示。
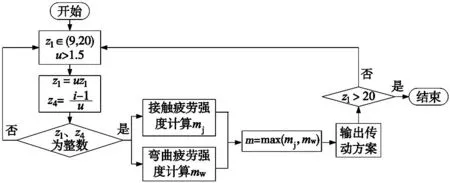
圖2 主要參數計算流程圖
通過圖3所示的計算方法進行參數迭代計算,能夠得到多組符合條件要求的幾何參數,如表1所示。

表1 符合約束條件的幾何參數方案

表2 選擇的幾何參數方案
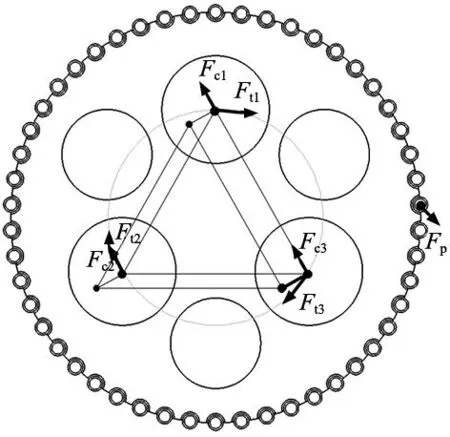
圖3 擺線輪受力分析
在選擇傳動比分配方案時,為保證運動平穩性、傳動效率與前后端工作壽命相同,機構整體尺寸小,一二級減速機構的結構尺寸應盡量相同,傳動效率應保持較高水平。因此應選擇第3個傳動方案。
1.2.2 關鍵尺寸設計
(1)關鍵零部件受力分析。
①擺線輪受力分析。在曲軸自轉下,擺線輪通過偏心運動與針齒嚙合在運動過程中,認為在擺線輪、曲柄、滾動軸承等零部件不存在尺寸誤差且材料處處均勻的理想狀態下,可認為曲柄沿針齒對擺線輪的力FP方向上曲柄軸產生的彈性形變相等。即曲柄軸承處FP方向上的受力均為FP/3;同時為抵消FP對擺線輪產生的扭矩,各曲柄軸承處沿擺線輪周向的受力也相等。如圖4所示,結合上述分析,曲柄受力的大小相等,合力與曲柄轉角θ有關。由此可得:
(4)
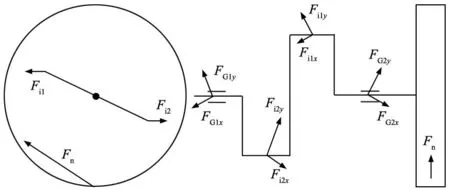
(a) 徑向受力分析 (b) 軸向受力分析
圖5 減速器主要幾何約束

(a) 曲軸 (b) 擺線輪 (c) 針齒殼 (d) 裝配體
式中:a為齒輪中心距,rRV為擺線輪半徑,αc為FP與擺線輪圓周切向的夾角。
②曲軸受力分析。由圖4b所示,通過擺線輪受力分析與力矩平衡方程可知作用力Fi1、Fi2和Fn已知,只有曲軸兩端的FG1、FG2未知,通過水平面與垂直面的力與力矩的平衡方程可得式(5)。
(5)
式中:bB為曲軸兩端軸承厚度,bD為曲柄處軸承厚度,bP為行星輪齒厚,Fnx與Fny為齒輪見嚙合力在x、y方向上的分量。
(6)
通過以上受力分析,結合減速器工作原理,3根曲軸對輸出軸的扭矩應滿足設計要求即:
(7)
對上述方程組求解可得:
M=2FPrRVcosαc
(8)
如圖4a所示,取任一曲軸及與其相固聯的行星輪為分離體,由力矩平衡方程可知:
(9)
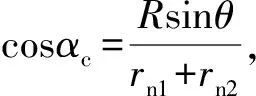
(10)
傳動過程中齒輪嚙合力Ft、針齒嚙合力FP、曲柄軸受力Fi、支撐軸承軸力影響FG,各力的表達式如式(11)所示。
(11)
(2)減速器關鍵參數分析。為保證RV減速器的體積、工作壽命符合設計要求,提高減速器的可靠性,針齒分布圓尺寸R應取值65,針徑系數K1應取值0.6。因此針齒殼上針齒直徑rn1應為rn1=KR=2.57。
分體式擺線輪的主要參數為:R、e、rRV、rn1、rn2。擺線輪傳動是依靠各對針齒的依次嚙合來實現的,為保證擺線輪能夠連續傳動,工作過程中應始終有至少一對針齒嚙合,即實際嚙合線的長度與針齒齒距的比值大于1。
為保證RV減速器在傳動過程中不發生干涉,任一針齒與相鄰針齒間距離應大于針齒直徑且針齒殼與擺線輪間應保留間隙,即:
①傳動過程中針齒殼上針齒與擺線輪間距離應大于0。
R>rRV+e+rn1
(12)
②傳動過程中擺線針輪機構能夠發生嚙合。
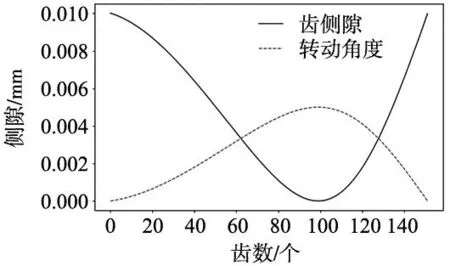
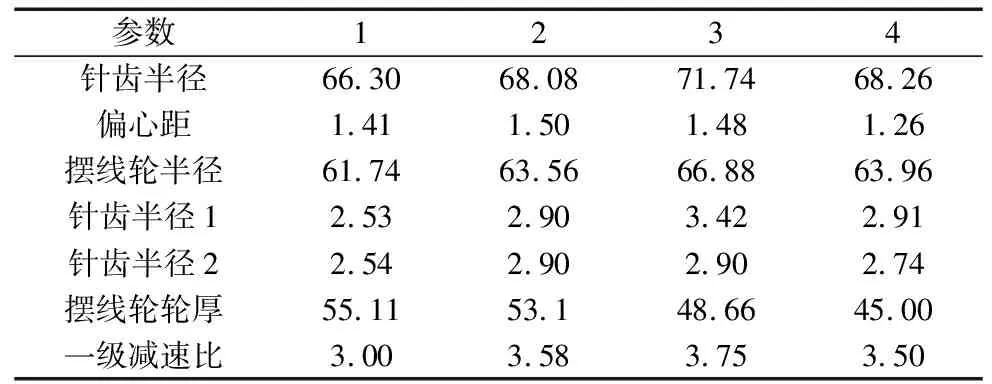
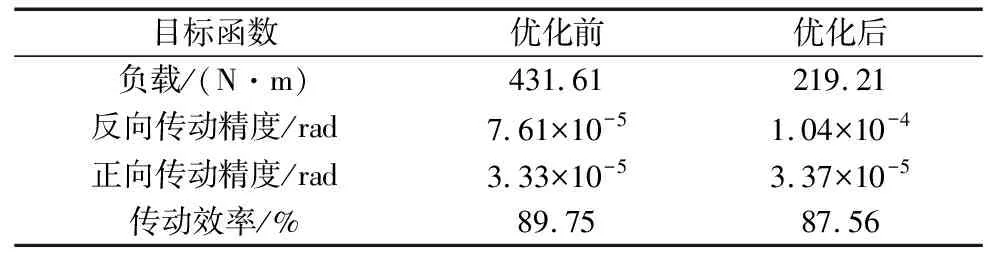
R (13) ③傳動過程中針齒間不能發生干涉。 R>rRV-e+rn1+rn2 (14) (15) ④回差是減速機精度標志之一,RV減速器的回差由幾何回差、溫度回差與彈性回差組成。其中幾何回差與傳動構件間的裝配空隙直接相關。為保證減速器的回差,針齒嚙合時擺線輪各尺寸應滿足: (16) 綜合上述分析,在K=1.67、R=59時,可得: 偏心距e在(1.42,1.48)的取值范圍內滿足幾何約束,由上述分析可知伴隨偏心距增大,減速器各處受力最小,同時在e=1.48時擺線針輪機構的回差最小。因此減速器各尺寸應為: (17) (3)軸承選型與關鍵零件設計。通過RV減速器受力分析可求解各部件受力為: (18) 由此曲柄軸承選用7004AC角接觸球軸承,曲柄兩端軸承選用30202圓錐滾子軸承,輸入軸與輸出軸軸承選用角接觸軸承71820AC。從而完成曲軸與連接盤的結構設計。 針對RV減速器衡量其性能的幾個關鍵技術參數有:負載性能,傳動效率,傳動精度等。為使減速器的性能達到理想效果,需要調整減速器的尺寸參數以進行結構尺寸優化。在求解過程中可以通過啟發式算法來求解。 NSGA是一種隨機全局搜索優化方法,從初始種群出發,通過模擬自然選擇和復制、交叉和變異等現象,產生一群更適合環境的個體,使群體進化到搜索空間中越來越好的區域,經過迭代,最后收斂到一群最適應環境的個體,從而求得問題的優質解。 2.1.1 目標函數 (1)正向傳動精度。分析RV減速器的運動可知,太陽輪帶動3個與偏置方向相同的曲柄軸固連的行星輪,同時在曲柄軸驅動擺線輪轉動時,曲柄軸與擺線輪鉸接點間的距離始終為定值,且等于相鄰行星輪間的距離,因此這個曲柄軸的轉動可視為以曲柄軸偏距為共用鄰邊的3個平行四邊形機構,通過對RV減速器結構進行高副低代得到等效桿長模型,如圖7所示。 圖7 等效桿長模型 將平行平面中的運動機構組合到同一平面中得到簡化模型,如圖8所示。 在不考慮加工誤差與裝配誤差時,運動學模型可表達為: (19) (2)傳動效率。在RV減速器工作過程中,傳動效率模型如式(2)所示。 (3)反向傳動精度。RV減速器是由行星傳動與擺線輪差齒傳動組成的閉環差動輪系,因此誤差計算包括行星輪系的回差與擺線針輪輪系的回差。 其中齒輪傳動部分的回差主要由齒側間隙造成,且回差經過擺線輪系會縮小為擺線輪系傳動比的倒數,由國家標準可知齒側間隙的取值為: (20) 因此齒輪傳動造成的回差為: (21) 擺線傳動部分的回差為: (22) (23) (4)負載性能。由于擺線輪輪齒的離散化,齒側間隙被放大,使同時嚙合的齒數減少。初始嚙合間隙的計算公式為: (24) 在對擺線輪加載扭矩后,擺線輪與針齒產生接觸變形,擺線輪轉過一個角度β: (25) 如圖9所示,初始間隙小于該角度的齒都參與嚙合,齒側間隙曲線為圖中實線,轉動角度曲線為圖中虛線,在交點內的齒是進入嚙合且受力的齒。 圖9 嚙合齒數 由赫茲公式可知,彈性變形量與受力的關系為: (26) 因此RV減速器的負載性能為: (27) 2.1.2 設計變量 由減速器運動學模型,以曲柄軸偏心距e、擺線輪基圓半徑rv、針齒分布圓半徑r、擺線輪針徑系數k1、針齒殼針徑系數k2和擺線輪齒厚b,設計變量基因型可表示為: x=[e,rv,r,k1,k2,b] (28) 2.1.3 約束條件 受加工條件與實際結構約束,設計變量存在取值范圍,不同設計變量間存在相互約束關系。 (1)為保證針齒殼與針齒之間的機械強度,同時避免針齒相撞,需要對針齒分布的稠密程度進行描述。在此引入針徑系數K1,通過針齒分布圓上相鄰兩針齒中心間的距離與針齒直徑的比值來表示: (29) 式中:K1?(1.5,2)。 (2)齒輪模數符合國標推薦模數; (3)傳動過程中零部件不發生干涉: (30) r>rv+e+r1 (31) (4)滿足連續傳動條件: r-e-rv≤r1+r2 (32) 對于針徑系數與齒輪模數等約束條件,通過設置取值上下限,連續傳動條件與干涉問題通過構造罰函數對樣本適應度進行修正。 f1=-e(r-e-rv-r1)2-r2(r-e-rv-r1) (33) (34) 由于尺寸參數優化具有多目標優化的特點,因此評價方法的不同會影響最終的計算結果,常見的評價方法是對不同優化目標分配權重,根據權重計算出評價最高的結果。但機構優化設計時,由于目標函數間存在相互沖突,會導致減速器尺寸結構失調,迭代結果無法使用。 因此,引入Pareto支配的概念,通過設置設計參數與目標函數的接受區間,若迭代結果無法在改進任何目標函數的同時不削弱至少一個其他目標函數時稱作Pareto最優解并接受。 在迭代過程中,為保證求解結果時全局最優,對迭代結果進行非支配排序,在同一層次的樣本進行擁擠度計算,對密集分布的樣本進行抽取,以保證樣本基因型的多樣性。擁擠度計算方法為: c=∑Δfi (35) 算法計算流程如圖10所示。 圖10 優化過程 通過NSGA-Ⅱ算法求解RV減速器結構參數的Pareto解。整體優化過程和各子目標的優化過程如圖11~圖15所示。 圖11 優化流程 圖13 反向傳動精度優化過程 圖15 傳動效率優化過程 圖16 RV減速器裝配體模型 在計算結果中選取4組最優結果,如表3所示。 表3 NSGA計算結果表 (mm) 由于各目標函數之間存在沖突,且不同目標間優先級也存在不同,設計綜合目標函數對優化問題進行描述,如式(36)所示。 Objective=∑(ωiXi)/SFi (36) 式中:權重系數ωi表征不同目標函數之間的優先級,比例因子SFi對各目標函數進行歸一化處理避免不同目標之間存在較大數量級的差距。本研究以優化傳動精度與負載性能為主,引入權重系數與比例因子如式(37)所示。 (37) 在計算結果中選擇綜合目標函數最小的一組解作為最優解。最終關鍵尺寸參數結果如表4所示。 表4 關鍵尺寸參數 (mm) 如表5所示,通過對比RV減速器優化前后性能變化可知,負載性能提升96.87%、反向傳動精度提升26.8%,正向傳動精度提升1.2%,傳動效率提升2.19%。 表5 優化結果對比 利用虛擬樣機仿真驗證設計RV減速器的運動可行性與傳動高效性,通過solid works分別對優化前后兩種RV減速器進行參數化建模,在確保正確裝配與無干涉后,將模型導入Adams并添加相關約束,通過不同轉速、負載之間的相互組合設置多種工況,以探究轉速、負載交互作用下RV減速器的傳動性能的變化規律。 將RV減速器裝配體模型以X_T格式導入ADAMS中,并給各關鍵零部件定義材料屬性,RV減速器的材料屬性如表6所示。 表6 RV減速器關鍵構件材料屬性表 在對RV減速器施加幾何約束后,設置RV減速器的太陽輪為轉動驅動,仿真轉速為2400 rpm,輸出盤理論輸出轉速為95 (°)/s。同時設置輸出端負載為空載,獲得RV減速器輸出端轉速如圖17所示,圖中RV減速器輸出端的實際轉速與理論輸出轉速近似相等,可以說明模型內部運動傳遞關系正確,同時對比輸出曲線可以看出,優化后RV減速器仿真結果相較于優化前RV減速器,由于針齒結構的幾何特點,內部零部件的間隙能夠得到有效控制,導致輸出端的響應速度要快于優化前RV減速器。 圖17 輸出端實際角速度對比圖 通過虛擬樣機仿真,獲得RV減速器在太陽輪輸入轉速2400 rpm下,輸出軸負載425 N·m的工況下輸出端角速度曲線,如圖18所示。從圖18a中可以看出,在相同工況下,減速器效率相同,由圖18b和圖18c可知,優化后減速器的曲柄軸與針齒等關鍵零部件受力更小,機構可靠性更高。 (a) 負載條件下輸入軸扭矩 (1)針對擺線輪廓形復雜、加工難度大的問題,采用分體式擺線輪對減速器進行優化設計,建立RV減速器三維模型,以負載性能,傳動精度,傳動效率為評價指標,構建多目標評價函數,采用NSGA算法實現RV減速器最佳結構參數集成。 (2)對優化設計出的RV減速器進行動力學仿真與有限元仿真分析,動力學仿真結果表明設計出的RV減速器負載性能提升96.87%、反向傳動精度提升26.8%、正向傳動精度提升1.2%、傳動效率提升2.19%,驗證了設計方法的有效性。同時采用有限元對設計RV減速器結構的合理性進行了驗證。2 尺寸參數優化
2.1 優化模型建立

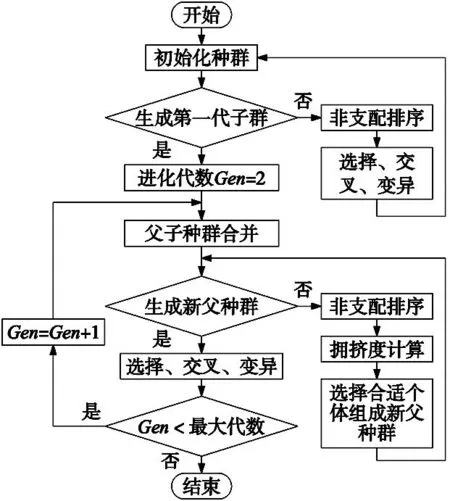
2.2 Pareto支配
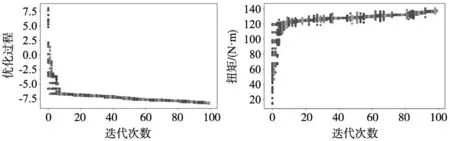
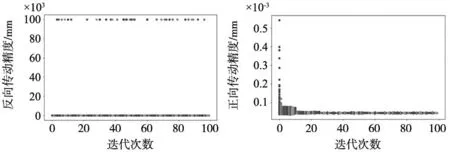
2.3 結果分析



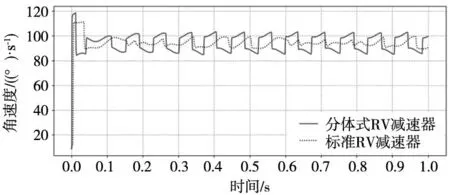
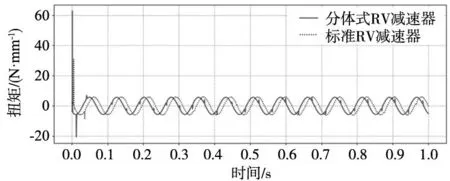
3 RV減速器仿真分析

4 結論

