基于非奇異負載轉矩觀測器的永磁同步電機抗擾動控制*
彭 誠,王 兵,郭皓源,李 羅
(湖南工業大學a.電氣與信息工程學院;b.電傳動控制與智能裝備湖南省重點實驗室,株洲 412007)
0 引言
永磁同步伺服系統相比于其他同步電機擁有調速范圍寬、系統精度高、消耗小和動態轉矩快等優勢,在數控機床、卷繞機、汽車工業和機械臂等相關領域上已被廣泛應用[1-3]。永磁同步電機(permanent magnet synchronous motor,PMSM)伺服系統能夠實現高精度的位置、速度控制,但PMSM在復雜工況下容易受到未知擾動(如負載轉矩變化、轉動慣量變化、粘滯摩擦系數變化)的影響,使伺服系統控制性能下降。許多先進控制方法被廣泛應用在PMSM的高性能應用場合,如反演控制[4]、魯棒控制[5]、自適應控制[6-7]、預測控制[8-9]、滑模控制(sliding mode control,SMC)[10-12]。上述控制方法對數學模型依賴性高,擾動影響大。
FLIESS等[13]提出無模型控制(model-free control,MFC)方法,降低了對具體數學模型的依賴,避免了未知擾動對電機控制性能的影響。王兵等[14]認為電機擾動主要來自負載轉矩和轉動慣量的變化,采用了改進型擾動滑模觀測器,將負載轉矩實時地觀測出來,從而通過前饋補償,來減少對系統擾動地影響。李先弘等[15]采用龍伯格狀態觀測器來觀測負載轉矩的控制策略,抑制負載擾動對于電機伺服系統控制性能的影響。越來越多的學者都采用非奇異快速高階滑模來代替PI控制方式來控制電機速度,但有一部分學者忽略了慣性負載對控制系統的影響。
本文為增強控制系統的抗擾性,提高控制精度,將MFC和非奇異終端滑模觀測器(nonsingular terminal sliding mode observer for load torque,LT-NTSMO)結合設計一種無模型非奇異終端滑模負載轉矩觀測器,實時精準觀測出負載轉矩,進行前饋補償,同時采用模型參考自適應算法(model reference adaptive control,MRAC)辨識電機轉動慣量,將慣量輸入到負載轉矩觀測器,有效抑制負載擾動對控制系統的影響。
1 PMSM數學模型
永磁同步電動機在d-q軸旋轉坐標系下的數學模型:
(1)
式中:ud、uq分別為d、q軸電壓,id、iq分別為d、q軸電流,Ld、Lq分別為d、q軸電感,ψd、ψq分別為d、q軸磁鏈,Rs為定子電阻,ψf為永磁體磁通,J為轉動慣量,p為極對數,B為粘滯系數,ωr為機械速度,ω為電角速度,Te為電磁轉矩,TL為機械負載轉矩。
2 負載轉矩觀測器
2.1 傳統負載轉矩觀測器
滑模控制系統因滑模存在固有抖振,當受到負載轉矩擾動及其他因素變化時,通過調整控制器幅值來對抗負載擾動,從而加大滑模的抖振。為減小滑模控制系統的抖振,采用觀測器對負載轉矩進行實時觀測,將觀測值轉換為電流值,進行前饋補償,能夠有效抑制負載擾動,削弱系統抖振。
(2)
在式(2)基礎上,將ωm與TL為觀測對象,建立一階滑模負載轉矩觀測器。
(3)

根據式(3)構建如圖1所示的負載轉矩滑模觀測器的原理框圖,由式(2)和式(3),得到滑模觀測器誤差式為:
(4)
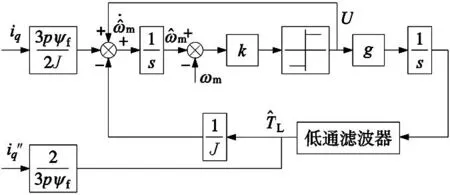
圖1 傳統滑模負載轉矩觀測器原理框圖

選取滑模面s1,令s1=e1。當滑模系數滿足條件k≤-|e2/J|,且g<0時,系統漸近穩定,滑模可達。可得轉矩觀測誤差方程為:
(5)
式中:C為常數。由上式可知,反饋增益g越小,收斂越快;相反,反饋增益g越大,收斂越慢。
2.2 非奇異終端滑模負載轉矩觀測器
由于傳統一階滑模負載轉矩觀測器,受反饋增益g的取值的影響很大,快速準確觀測出各種內外擾動存在難度,為快速準確地觀測出各種內外擾動,本節設計一種非奇異快速終端滑模擾動負載轉矩觀測器,實時觀測各種內外擾動,將擾動轉化為負載觀測值,結合控制器對iq進行補償,減少負載變化及其他擾動給系統帶來的不穩定性,達到提高控制精度的目的。狀態方程選擇可以用于內置式和表貼式永磁同步電機的運動式為:
(6)
在式(6)基礎上,將TL與ωm為觀測對象,建立如下負載轉矩觀測器:
(7)
引入超局部模型公式[16]:
(8)
引入狀態量為:
(9)
(10)
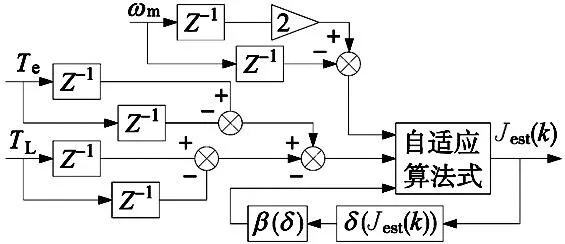
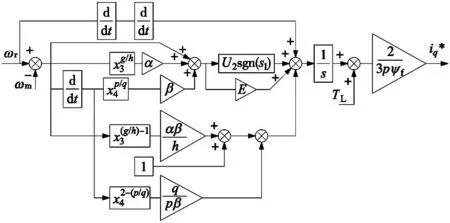
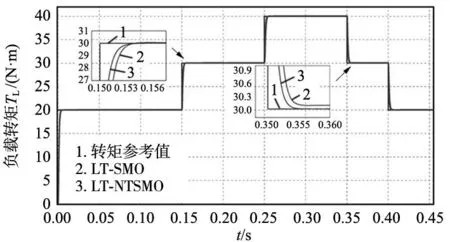
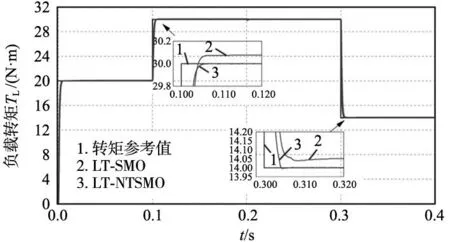
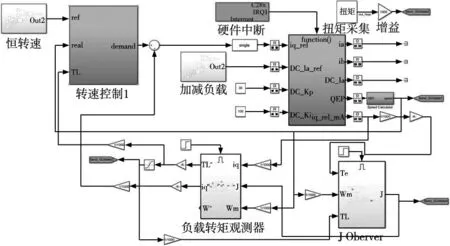
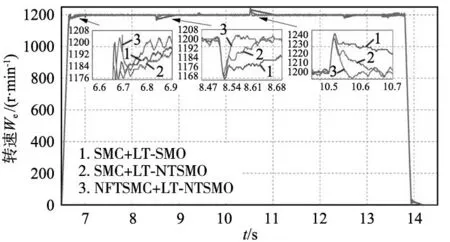
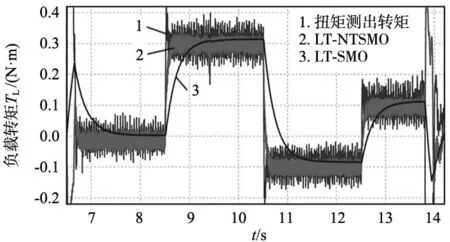
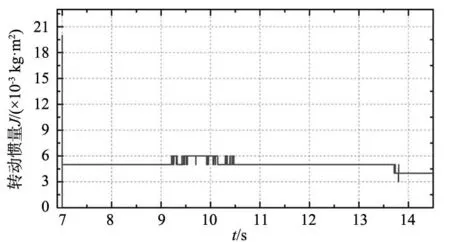
式中:λ1=1,λ2為大于0的常數,z、t均為奇數,1 對式(10)求導可得: (11) 如果選擇非奇異終端滑模面,并且控制律設計如下,則狀態誤差可以在有限時間內收斂到0。 (12) 式中:l1>0,l2>0是設計參數。通過U1所構建的負載轉矩觀測器原理圖如圖2所示。 圖2 非奇異終端滑模負載轉矩觀測器原理框圖 證明負載轉矩觀測器系統穩定性,選用Lyapunov函數: (13) 將V1進行開導,并將式(12)帶入,則得到以下方程: (14) 根據Lyapunov穩定性判別定理和滑模可達條件可知,所設計的非奇異終端滑模將有限時間內收斂。由于F為式(8)中的未知項,設計了滑模觀測器來獲得估計值為: (15) 式中:k1為設計參數,x為狀態變量ωm。 觀測誤差定義為: (16) 對式(16)求導可得: (17) 選擇滑模面S2=e3,如果選擇適當的k1,誤差方程(17)將在有限時間內收斂到0。 證明超局部模型系統穩定性,選用Lyapunov函數: (18) 對式(18)求導可得: (19) 當k1>|F|+η(η>0),根據式(19)得到式(20): (20) 根據Lyapunov穩定性判據和滑模可達性條件,誤差e3將在有限時間內收斂到0,因此,觀測器是漸進穩定的。 (21) 根據式(7)、式(12)和式(21)可以構成非奇異終端滑模負載轉矩觀測器,觀測器原理圖如圖2所示。 帶慣性負載時,系統的轉動慣量會發生改變,因此辨識出伺服系統轉動慣量十分重要,轉動慣量辨識精度將直接影響伺服系統響應。根據電機數學方程和離散原理搭建參考模型,得到k時刻的ωm(k);將離散周期和轉動慣量的比值作為可調參數,構建可調模型,得到k時刻的估計值ωg(k);由于兩個模型物理意義相同,將誤差通過辨識算法無限逼近。 將式(1)中的運動方程進行離散和簡化可得: (22) 式中:T是系統采樣周期。 ωm(k)=2ωm(k-1)-ωm[(k-2)+ (23) 式中:b=T/J,ΔTe(k-1)為一個采樣周期的電磁轉矩的差值,ΔTL(k-1)為一個采樣周期的負載轉矩估計值之差。根據參考模型式(23),構建可調模型如下: ωg(k)=2ωm(k-1)-ωm(k-2)+ (24) 式中:ωg為估計的速度信號。 可得出永磁同步電機轉動慣量MRAS規律: (25) 式中:β1為自適應增益系數,Δω(k)為參考模型方程的計算速度和可調模型的估計速度之差,Δω(k)=ωm(k)-ωg(k)。 依據MRAS算法的原理,辨識電機慣量的原理如圖3所示。在MRAS算法中,辨識系數的大小直接影響轉動慣量辨識精度和辨識的收斂速度。辨識系數大,辨識速度快,但辨識精度下降,辨識系數過小,辨識速度慢,影響負載轉矩的觀測。本文采用辨識增益自適應,對實時辨識結果進行分析,選擇最優的辨識系數。 圖3 辨識電機慣量原理圖 設當前為第k個辨識周期,取最新的n+1個轉動慣量辨識數值分別為:Jest(k),Jest(k-1),…,Jest(k-n)。 由以上轉動慣量辨識值構建評價標準: (26) 式中:G為增益,引入函數: (27) 根據δ的變化來選擇最優的辨識增益β1,構建以下函數: β1=δ*βmax (28) 式中:βmax為最大辨識系數。辨識慣量結構框圖如圖4所示。 圖4 辨識慣量原理框圖 為了快速跟蹤和有效抑制轉速抖振,速度控制器采用滑模變結構控制,滑模面采用非奇異快速終端滑模,同時將負載轉矩觀測器觀測的負載轉矩觀測值引入的控制器中,實現了抑制負載變化,減小速度波動,切換增益小,收斂速度快的良好控制性能。 永磁同步電機伺服系統的數學模型為: (29) 選擇NFTSMO滑模面為: (30) 式(30)求導可得: (31) 文中選擇指數趨近律為: (32) 由上可知速度環的滑模控制律為: (33) 速度環穩定性分析,選取Lyapunov函數: (34) 式(34)求導可得: (35) 因此,可知文中所設計的滑模控制器穩定。 由式(33)構建NFTSMC轉速控制結構框圖,如圖5所示。結合負載轉矩觀測器,慣量辨識觀測器和速度控制器所搭建的系統控制框圖,如圖6所示。 圖5 NFTSMC轉速控制器結構框圖 圖6 系統控制框圖 本節通過仿真和硬件在環實驗來驗非奇異滑模負載觀測器的有效性,將負載轉矩線性滑模觀測器和非奇異終端負載轉矩滑模觀測器進行對比仿真,對比系統采用相同控制策略。速度環使用非奇異快速終端滑模控制器,電流環使用PI控制。 表1 永磁同步電機參數值 線性滑模負載轉矩觀測器控制參數為:k=4000,g=-10;非奇異終端滑模負載轉矩觀測器控制參數為:λ1=1,λ2=5,z/t=7/5,l1=1500,l2=5000,k1=100,g1=-10;速度控制器alpha=0.000 78,bata=0.000 48,E=410,U2=6×106,g/h=9/5,p/q=9/7;電流控制器d、q軸相同Kp=15,Ki=3000。 為測試系統在受到負載轉矩擾動是控制性能,初始時刻負載轉矩TL=20 N·m,在運行0.15 s、0.25 s、0.35 s和0.4 s時進行負載轉矩突變,分別給定為30 N·m、40 N·m、30 N·m和20 N·m,在0.2 s轉動慣量產生變化,并在0.3 s轉動慣量值恢復到原值。在轉速給定維持在1500 r/min時,兩種觀測器控制策略下,系統受到多次負載轉矩加載、減載變化,仿真結果如圖7~圖9所示。 圖7 負載突變工況下轉速對比圖 沒有負載轉矩觀測補償,加載或減載時還是存在對系統穩定運行影響,NFTSMC+LT-NTSMO控制可以比其他兩種控制策略更快地恢復到給定轉速。從圖8可以看出,LT-NTSMO相比與LT-SMO轉矩響應更快觀測,同時精準地對轉矩值進行估計。從圖9可以看出,轉動慣量觀測器能快速準確的觀測出轉動慣量的實際值,同時能觀測到負載轉矩變化對轉動慣量的影響。 圖8 負載轉矩突變工況下兩種觀測器觀測轉矩對比圖 圖9 負載轉矩突變工況下轉動慣量觀測轉動慣量圖 為了驗證系統在轉速突變工況下控制性能,給定負載轉矩20 N·m,設定系統初始轉速為1500 r/min,在運行0.2 s和0.4 s時進行轉速突變,分別給定為1000 r/min和500 r/min,并在0.1 s和0.3 s進行加載和減載的負載轉矩突變。在0.2 s轉動慣量產生變化,并在0.3 s轉動慣量值恢復原值。兩種控制策略下轉速突變工況下轉速對比仿真結果如圖10所示,變轉速工況下兩種觀測器觀測負載轉矩對比如圖11所示,變轉速工況下轉動慣量如圖12所示。 圖10 變轉速工況下轉速對比圖 圖11 變轉速工況下兩種觀測器觀測負載轉矩對比圖 圖12 變轉速工況下轉動慣量圖 當系統在不同轉速下運行遇到加載或減載時,由圖10可以看出,沒有負載轉矩觀測補償,加載或減載時還是對系統穩定運行產生影響。在圖11所示,由LT-NTSMO控制,轉矩響應更快觀測更精準。圖12中轉動慣量能很好的觀測出,但在負載變化時,觀測出現了波動。 PMSM硬件在環實驗平臺由電機對拖平臺和多電機綜合驅控實驗平臺組成,實驗平臺采用MATLAB/Simulink和TMS320F28335DSP為核心的軟件和硬件相結合,仿真模型下載到嵌入式設備上,實現電機控制。實驗采用永磁同步電機和直流電機對拖,PMSM控制系統仿真模型圖如圖13所示,采用永磁同步電機和直流電機對拖,實物平臺實物照片如圖14所示。 表2 永磁同步電機參數值 圖13 PMSM控制系統仿真框圖 圖14 實物平臺實物照片 為驗證在恒轉速變負載工況下負載轉矩和轉動慣量觀測進行前饋補償控制策略的控制效果,進行驗證分析。在實驗平臺上,電機空載啟動。實驗運行時間為7.3 s,給定系統轉速1200 r/min,在8.5 s時由0 N·m增加到負載0.285 N·m,在10.5 s時將負載轉矩突減到-0.1 N·m,在12.5 s時不給予被拖直流電機給定電流,負載轉矩變成0.095 N·m。 在相同的實驗條件下,分別做了3組實驗進行對比,分別是用SMC加LT-SMO進行電機實驗、SMC和LT-NTSMO進行電機實驗和NFTSMC器加LT-NTSMO進行電機實驗。線性滑模負載轉矩觀測器控制參數為:k=4000,g=-10;非奇異終端滑模負載轉矩觀測器控制參數為:λ1=1,λ2=5,z/t=7/5,l1=3,l2=2,k1=8,g1=-5;速度控制器alpha=0.005 85,bata=0.55×10-3,E=163,U2=798,g/h=9/5,p/q=9/7。電流控制器d、q軸相同Kp=200,Ki=20。通過實驗,得到3種控制策略下的對拖平臺轉速對比圖如圖15所示,兩種負載轉矩觀測器觀測轉矩的對拖平臺轉矩對比圖如圖16所示,模型自適應轉動慣量觀測的對拖平臺慣量如圖17所示。 圖15 對拖平臺轉速對比圖 圖16 對拖平臺轉矩對比圖 圖17 對拖平臺慣量觀測圖 電機以某一轉速運行,有LT-NTSMO估計的補償電流值的控制策略,相比于LT-SMO估計的電流值補償控制策略能更快恢復到給定轉速。通過控制被拖電機來實現負載擾動,從圖16中可以看到,LT-NTSMO觀測出的負載轉矩相比于LT-SMO觀測的響應速度更快,數據更加接近于有扭矩檢測器測的轉矩,也可以看出通過對拖平臺跑出來的負載轉矩存在波動。由圖17可以知道,模型自適應慣量觀測器觀測出系統慣量為5×10-3kg·m2,但在中間產生振動。通過觀測器觀測的系統慣量的數值比電機慣量要大。 通過觀測器觀測的系統慣量為永磁同步電機和直流電機及連接器的轉動慣量的總和,在環平臺實驗結果和仿真結果證明,慣量觀察器能準確觀測出系統慣量。根據MATLAB仿真和硬件在環實驗平臺結果,可以得到非奇異終端滑模負載轉矩觀測器觀測的負載轉矩效果更好。 本文在對PMSM負載擾動觀測器研究的基礎上,采用了自適應算法將轉動慣量實時辨識并送入負載轉矩觀測器中,采用了非奇異終端滑模負載轉矩觀測器,觀測電機負載轉矩,并進行補償。仿真和在環實驗結果均表明,設計的控制策略能較好觀測負載轉矩和轉動慣量,當發生負載變化和慣性負載變化時,設計的非奇異終端滑模負載轉矩觀測器具有快速的辨識能力,通過前饋補償,有效減少了擾動帶來的影響,提高了電機控制精度。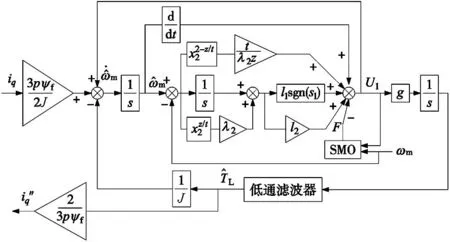
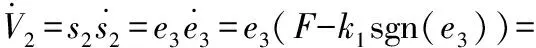
3 轉動慣量辨識
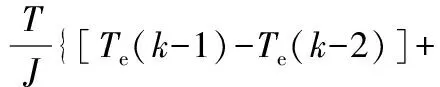
b(ΔTe(k-1)-ΔTL(k-1)]
bg(k-1)(ΔTe(k-1)-ΔTL(k-1))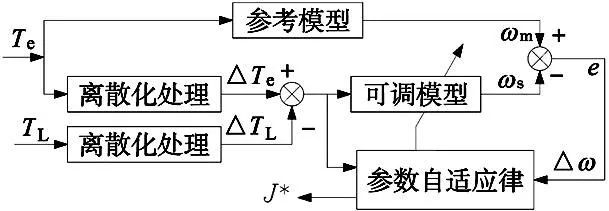
4 滑模速度控制器

5 實驗驗證

5.1 負載突變分析
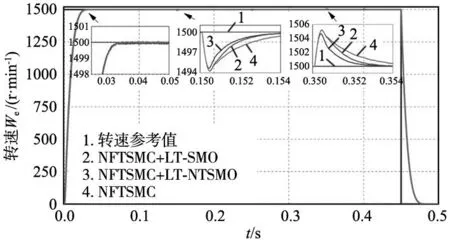

5.2 轉速突變分析


5.3 硬件在環實驗平臺驗證


6 結論

