基于載荷譜的電池包疲勞試驗與計算方法

上官文斌 岳煉 呂輝 周孚鵬

（1.華南理工大學 機械與汽車工程學院，廣東 廣州 510640；2.祥鑫科技股份有限公司，廣東 東莞 523870）

電池包作為新能源汽車的重要組成部件，不僅起著儲存、傳輸電能的作用，其安全特性更是直接關乎電動車的安全可靠性。電池包作為“三電”系統的核心部件，大多直接安裝在汽車底盤下方，承受來自路面和電機的各種激勵。因此，保證電池包具有足夠長的疲勞耐久壽命以滿足電動車的使用周期，已成為整車研發的重點關注對象［1］。

對于電池包的疲勞壽命預測，相關研究人員基于有限元分析和數值理論提出了相應的計算方法。但是在這類研究當中，大多數分析計算得出的結果，均缺少相應的試驗驗證，無法證實計算分析方法的可靠性。更為重要的是，研究人員在建立電池包的疲勞壽命分析模型時，僅僅對電池箱體進行了粗略的建模，對電池箱體結構進行了一定的簡化，同時電池模組均是用方形質量塊［2］或者質量點［3］代替，忽略了電池模組中各零部件的疲勞失效。對于電池包內的連接方式，進行了一定的簡化，將焊接和螺栓連接采用剛性連接代替［4］，忽略了連接方式的疲勞失效，無法保證仿真分析結果的可靠性。同時，對于電池包的振動試驗，相關研究人員花費了大量的精力在探究電芯的振動試驗［5-8］或者電芯支架的振動試驗［9］，提出了針對電芯的振動試驗方法，但是無法普及應用到電池包的隨機振動試驗中。因為電芯體積小、質量輕，很容易保證振動信號的準確傳遞，但是電池包體積大、質量大，在隨機振動試驗中，振動信號在傳遞過程中很容易產生誤差。因此在電池包的隨機振動試驗中，為了確保試驗的準確性，保證振動信號的傳遞非常重要。

本文以電動車電池包為研究對象，研究了電池包隨機振動試驗方法和疲勞特性的計算方法。首先提出了驗證振動信號在振動臺、工裝夾具、電池包之間傳遞的方法，給出了電池包結構和功能上的系統性檢查方法；然后對電池包進行隨機振動試驗，并檢查出電池包的損傷部位。最后提出了電池包疲勞損傷特性的計算方法，基于電池包精細化模型，采用Goodman疲勞壽命估算方法和Miner線性累積損傷法則，對電池包進行了隨機振動疲勞損傷分析。將分析得到的電池包疲勞損傷部位與試驗結果進行對比，驗證了計算方法的準確性，對后續電池包的疲勞特性的研究有一定的參考作用。

1 電池包疲勞試驗

在對電池包進行隨機振動試驗前，需對振動信號傳遞路徑進行檢查，確保振動臺發出的信號傳遞到電池包與工裝的連接處。試驗后需對電池包進行結構與功能性檢查，以確認電池包是否在隨機振動過程中發生損壞。

1.1 疲勞試驗的載荷

在隨機振動試驗中，輸入的載荷譜要和電池包在實車運行中所受到的載荷一致。為得到符合實際行車工況中電池包的輸入功率譜密度，本文通過對電動汽車在各典型工況行駛時采集并處理得到電池包與車身連接處的功率譜密度，用以模擬電池包在實車運行中所受到的載荷。

在城市道路、鄉村公路、高速路和壞路等典型道路條件下，在電池包與車身連接處布置加速度傳感器，通過實車路譜采集試驗，得到了車輛運行過程中電池包與車身連接部位的加速度信號。隨后基于等損傷原則，計算得到電池包隨機振動試驗所需的功率譜密度曲線［10］，如圖1所示。動力電池需滿足使用年限達到5～8年或行駛十萬公里的設計要求，依據等損傷原則，為模擬電池包在使用年限期間所受到的隨機振動造成的損傷，要求各個方向振動時間不低于48 h。

圖1 電池包隨機振動功率譜密度曲線Fig.1 Random vibration power spectral density curve of battery package

1.2 振動試驗方法

振動試驗流程如下：選取3個同樣的電池包作為樣包用于隨機振動預實驗，命名為A號、B號、C號，分別在3臺振動臺上同時進行X，Y，Z方向上的隨機振動，驗證系統工作是否正常并且探究電池包在單方向振動中的損傷狀況。本章以X向隨機振動為例對試驗方法進行介紹。

1.2.1 振動加速度的頻響特性

將加速度傳感器均勻地布置在臺面、夾具和電池包上，通過對比傳感器測量示數與輸入加速度值，即可驗證振動信號的傳遞。各個加速度傳感器的編號和安裝位置如圖2所示。

圖2 傳感器布置位置Fig.2 Sensors location

（1）振動臺臺面加速度

為確保輸入的振動信號傳遞至振動臺，對振動試驗臺進行空載掃頻試驗，掃頻范圍選取為5～250 Hz。同時，為了盡可能的減少掃頻對夾具和電池包的損害，在能夠順利進行掃頻試驗的前提下，掃頻加速度則需要越小越好，因此選取振動系統的最小穩定振動加速度a=0.5g。設定掃頻停機上下線與警告上下線，圖3中分別用紅色實線與黃色虛線表示。若加速度曲線超過警告上線且出現明顯峰值，則結構出現共振，峰值所對應的頻率為結構的共振頻率。因此規定掃頻得到的加速度曲線應在加速度警告線內，以確保振動信號傳遞至振動臺。

圖3 振動臺臺面加速度頻率響應特性曲線Fig.3 Acceleration frequency response curves of shaker table

圖3為振動臺X方向掃頻結果。由圖可見，振動臺臺面X向的加速度頻響曲線均在規定范圍內，表明輸入信號能夠準確地傳遞至振動臺臺面。

（2）工裝空載端板處的振動加速度

對工裝進行空載掃頻試驗，測量得到工裝空載端板處加速度頻響特性曲線如圖4所示。

圖4 工裝空載端板處加速度頻響特性曲線Fig.4 Acceleration frequency response curves at the no-load end plate of the fixture

由圖4可見，在高頻范圍內（大于150 Hz），工裝夾具振動加速度值出現較大波動，這是因為工裝夾具并不是一個完全剛性的體系。但在電池包隨機振動的規定頻率范圍內（5～150 Hz），測得的加速度均在規定范圍內，該工裝夾具符合試驗要求。

（3）工裝端板及電池包上振動加速度

將電池包安裝至工裝上，對電池包進行掃頻試驗，圖5為電池包X方向掃頻結果。

圖5 X向電池包掃頻結果Fig.5 Frequency sweep results in X axis

由圖5（a）可見，在5～150 Hz頻率范圍內，電池包與工裝連接端板處傳感器測量得到的振動加速度值均位于規定范圍內，表明振動信號準確地傳遞至電池包。同時由圖5（b）可得電池包共振頻率，用作后續對比。

1.2.2 電池包隨機振動

在完成以上振動信號的檢查之后，對電池包進行隨機振動試驗。輸入隨機振動功率譜密度參數，以X向隨機振動試驗為例，圖6為隨機振動中工裝與電池包連接平臺上傳感器測得的功率譜密度曲線。由圖6可得，電池包隨機振動試驗時，工裝與電池包連接平臺上的振動信號與振動臺面輸入功率譜密度曲線變化趨勢一致，進一步證實了振動信號能夠較為準確地傳遞至電池包。

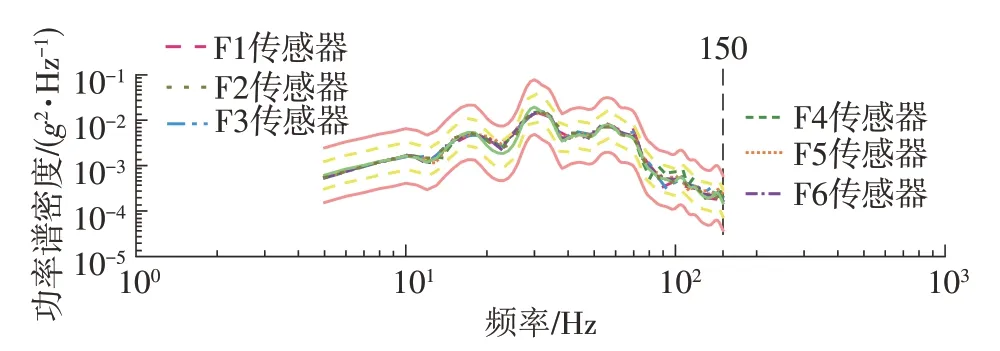
圖6 電池包X向隨機振動功率譜密度曲線Fig.6 X axis random vibration PSD curves of battery package

在A號和B號電池包的隨機振動試驗完成后，讀取BMS監測設備監測參數，電芯各性能參數無明顯改變，證實了電池包試驗前后功能無損壞。

C號電池包在Z方向隨機振動過程中突然出現異響，為防止電池包出現進一步的損壞而引發火災或爆炸等危害，及時停止試驗，等待進一步的檢查。

1.3 電池包隨機振動結果分析

1.3.1 電池包共振頻率分析

隨機振動試驗結束后，對完成隨機振動測試的A號電池包和B號電池包進行共振頻率分析。振動前后電池包共振頻率對比如表1、表2所示。

表1 X向振動前后電池包共振頻率對比Table 1 Comparison of battery package resonance frequencies before and after X axis vibration

表2 Y向振動前后電池包共振頻率對比Table 2 Comparison of battery package resonance frequencies before and after Y axis vibration

由表1和表2可知，電池包隨機振動前后共振頻率相差均小于10 Hz，因此判定電池包X和Y向隨機振動對電池包結構無明顯損壞。

1.3.2 電池包性能檢查

為進一步檢查電池包性能，對隨機振動后的電池包進行各項性能檢查，檢查結果為：

（1）A號和B號電池包壓降分別為22.9和20.4 Pa，絕緣電阻均為10 MΩ/V。各項性能仍能滿足設計要求，電池包安全地通過隨機振動試驗。

（2）C號電池包壓降為121 Pa，超過100 Pa，斷定為電池包氣密性失效，電池包結構在隨機振動中發生損壞。對C號電池包進行更全面的拆包檢查，檢查得出C號電池包損傷位置如圖7所示。

圖7 C號電池包損傷部位檢查Fig.7 Inspection for damaged parts of battery package C

對C號電池包損傷部位進行分析得出，前3處損傷均是由于結構強度不足導致的振動開裂，而最后一處托架與右側掛載點蓋板處開裂，是由于此處焊點工藝制造誤差導致虛焊，存在一定的偶然性。

2 電池包振動疲勞的計算與分析

2.1 電池包有限元模型的建立

有限元模型是疲勞分析的基礎和關鍵，為模擬電池包在振動工況中力的真實傳遞路徑，需要對電池包建立精細的有限元模型。

2.1.1 電池箱有限元模型

本文以電動汽車所裝配的電池包為研究對象，為盡可能的還原電池包內部各結構，對電池箱體進行了精細化建模，如圖8所示。

圖8 電池箱模型Fig.8 Battery package model

將三維模型導入HyperMesh有限元軟件中，進行有限元網格劃分。電池箱各零部件均為鋼板沖壓件，厚度均在3 mm之內，為保證計算精度并減少網格數量，各零部件均采用殼單元進行網格劃分。

2.1.2 模組有限元模型

模組作為電池包的主要零部件，其質量占據了整包質量的80%，本文為了更準確地模擬模組內部以及模組與電池箱之間力的傳遞路徑，以電芯為最小單元，對模組進行了精細化建模，如圖9所示。

圖9 模組三維模型Fig.9 Module digital model

將模組模型進行有限元網格劃分，不考慮電芯在振動工況中的失效，在分析中將電芯材料定義為可壓縮泡沫［11］，僅考慮電芯重量。電芯中的鈑金件均采用殼單元進行網格劃分，其余實體為保證網格質量，采用六面體網格劃分。

2.1.3 連接方式有限元模型

在電池包有限元模型中，為準確地模擬出電池箱內各零部件之間力的傳遞路徑，需對電池箱體內各零部件的連接方式進行精細化建模。

在沖壓電池箱體中，焊接作為主要的連接方式，且作為振動中較易失效的連接方式，必須在疲勞損傷分析中進行精確地模擬［12］。

不同的仿真分析模型所選擇的焊接建模方法各有不同。本文為精確地模擬出電池包中各零部件之間力的傳遞路徑，需在模型中精確地模擬出焊點、焊縫的位置和受力狀況，同時由于該電池包內焊點、焊縫數量眾多，對每個焊點、焊縫及其連接部件進行局部細化網格的話，網格數量太多、計算量大。因此本文所研究的電池包內的焊點均采用ACM2單元模擬，該焊點單元是由六面體單元模擬焊核，通過RBE3單元連接六面體單元和焊接面；焊縫均采用棱柱單元模擬，該焊縫單元是由棱柱單元模擬焊縫，通過RBE3單元連接棱柱單元和焊接面。

對于螺栓連接，在電池包內主要用于連接上蓋與箱體、模組與箱體，力的傳遞形式相對簡單，并且螺栓強度大而承受的力和力矩較小，因此為了減少分析計算時間，在本研究中不考慮螺栓的失效，采用RBE3單元和梁單元進行模擬。

2.2 疲勞壽命分析方法

對于本文所研究的電池包在隨機振動工況中，電池包各零部件的疲勞特性均屬于高周疲勞問題，因此本文采用適用于計算高周疲勞問題的名義應力法。

名義應力法（S-N法）作為最早的疲勞壽命預測方法，以材料疲勞特性參數曲線為基礎，以結構所受對稱循環等效應力為參數進行疲勞壽命的預測。因此，需將結構在實際工況中所受的實際應力轉換為對稱循環等效應力，消除平均應力對疲勞壽命的影響［13］。針對對稱循環等效應力的計算方法，本文為了保證計算結果的可靠性，采用計算相對較為保守的Goodman方法。

而振動疲勞破壞是由每次振動產生的損傷累積造成的，當損傷累積超過某一臨界值之后，結構便會發生疲勞破壞［14］。本文采用所需材料參數較少，形式簡潔且計算精度較高的Miner線性累積損傷法則對電池包疲勞損傷進行計算。

2.3 電池包振動疲勞分析

對電池包進行隨機振動疲勞分析，分析電池包可能出現的損傷部位與電池包隨機振動試驗形成對照，驗證電池包疲勞分析模型的準確性。

2.3.1 頻率響應分析

采用模態疊加法對電池包進行頻率響應分析，將電池包有限元模型導入Abaqus有限元分析軟件中，對電池包進行約束模態分析，得出電池包1～150 Hz范圍內的所有模態。

得到電池包模態頻率后，對電池包分別施加X、Y、Z方向上的單位加速度g（9.81 m/s2）載荷，進行5～150 Hz的掃頻分析，分別得到電池包在3個方向上的頻率響應，作為疲勞分析的關鍵輸入。

2.3.2 電池包疲勞壽命計算

本文采用nCode Designlife疲勞仿真軟件，該軟件可以通過材料的屈服極限、抗拉極限和彈性模量等參數對材料S-N曲線進行近似估算。

以X向隨機振動疲勞響應分析為例，將電池包的頻率響應分析結果導入疲勞分析軟件中，定義電池包材料參數，同時導入X向隨機振動功率譜密度曲線。將振動循環時間定義為48 h。使用Miner線性累積損傷法則，采用Goodman方法對平均應力進行修正，以消除平均應力對疲勞壽命的影響。

電池包的X向隨機振動疲勞損傷結果如圖10（a）所示。由圖可見，電池包最大損傷位置位于上蓋前部凸起與后部過渡處，最大損傷值為0.29，小于1（1表示經歷完整循環次數的隨機振動后零件剛好損壞），表明電池包在X向的隨機振動中無結構件損壞。

圖10 隨機振動疲勞損傷云圖Fig.10 Random vibration fatigue damage nephogram

Y、Z方向電池包隨機振動疲勞響應分析步驟與X向類似，不再贅述。電池包Y向隨機振動疲勞損傷結果如圖10（b）所示。由圖可見，電池包最大損傷位置位于上蓋后端左右角螺栓孔處，最大損傷值為6.09×10-4，遠小于1，表明電池包在Y向隨機振動中無結構件損壞。

電池包Z向隨機振動疲勞損傷計算結果如圖10（c）、10（d）所示。由圖可見，電池包最大疲勞損傷值大于1，分別位于上蓋前部凸起與后部過渡處（最大損傷值為2.78）、箱體與后掛載點搭接處（最大損傷值為1.27）、箱體與托架搭接處（最大損傷值為4.26），表明在Z向隨機振動過程中，電池包這3處位置出現疲勞損傷。

將電池包隨機振動試驗結果與有限元疲勞分析結果進行對比，如表3所示。由表3可知，X方向和Y方向電池包隨機振動疲勞分析結果與試驗結果一致，均為安全通過隨機振動試驗，電池包無損壞。Z方向電池包隨機振動試驗得到前3處損傷部位與分析得到的失效部位基本一致，但是最后一處（托架與右掛載蓋板處）分析與試驗結果出現差異。而在電池包隨機振動試驗時，對電池包進行拆包檢查時便已經得出，最后一處損傷為工藝制造誤差導致，存在偶然性。

表3 電池包疲勞分析與試驗結果對比Table 3 Comparison of analysis and test results of battery packages

綜上所述，基于本文提出的電池包疲勞損傷計算方法，對電池包隨機振動疲勞損傷部位進行預測，預測得到的損傷部位與試驗損傷部位具有較好的一致性，驗證了計算方法的準確性。

3 結論

（1）建立了電池包隨機振動的測試方法，最大限度的規避了試驗臺、夾具、電池包之間振動信號傳遞的誤差，保證了測試結果的準確性。同時還對電池包進行了結構和功能上的系統性檢查，確保了電池包檢查結果的全面性與可靠性。

（2）提出了電池包精細化建模方法，分別對電池箱、電池模組、電池包內各連接方式進行了精細化建模，保證了分析模型的完整性，進一步保證了分析結果的可靠性。

（3）基于電池包精細化模型，提出了電池包疲勞特性計算方法，對電池包進行隨機振動疲勞損傷分析。結果表明：仿真分析得到損傷部位與試驗得到的實際損傷部位具有較好的一致性，證實了計算方法的準確性與可靠性。