基于改進縮方差法的工期固定-資源均衡優化方法

高 婷

重慶交通大學,重慶 400074

0 引言

在網絡計劃中,最大資源需求量小于或等于實際可供應的資源,就是一個可行的網絡計劃。在建設工程施工中,當工期固定時,為減少資源浪費、降低成本,對資源配置進行優化以提高企業經濟效益。對于工期固定的資源均衡配置問題,常用的方法有很多,例如縮方差法(方差法)[1]、方差值最小法[2]、削峰填谷法[3]等。縮方差法在資源均衡配置中應用較廣。對于大型工程項目來說,網絡計劃的工序很多,若用原始的方法步驟求解,就會使有限時間內的優化工作變得不可行。因此,引入非關鍵工序組[4]的概念,將多個非關鍵工作放在一組進行調整,以減少調整步驟。原有方差法是對問題進行逐一試算、逐一調整,不能一次達到最大限度的資源均衡,特別是在大型網絡計劃中,使得計算和調整尤為繁瑣,降低優化效率。因此,引入最小方差法的概念,選擇使方差變化最大的移動時間作為調整時間。 本文結合非關鍵工序組概念與最小方差法對原有縮方差法進行改進,并給出非關鍵工序組調整判別式的一般化形式,進一步簡化了計算過程。

1 縮方差法

方差是衡量隨機變量或一組數據時離散程度的度量,概率論中方差用來度量隨機變量和其數學期望之間的偏離程度。網絡計劃中,把每項工作上所配備的資源看作隨機變量,利用時差來調整工作的開始時間和與完成時間以縮小方差,當這組隨機變量方差值盡可能小的時候,即資源得到盡可能均衡的分配。

縮方差法是利用平衡性指標作為網絡計劃實現資源優化的定量指標,以Δ作為判定是否進行資源調整的依據。當Δ≤0時,可以對非關鍵工作進行調整,調整后變小,說明資源得到更均衡的分配。

1.1 平衡性指標∑R2

資源消耗的均方差可用下式表示[5]。

(1)

(2)

1.2 調整判別式Δ

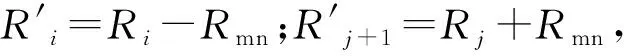
(3)

Δ′=Rj+1-Ri+Rmn

(4)

式中:若Δ<0,則∑R2減少,該工作可以進行調整;若Δ=0,則∑R2無變化,該工作可以不調整也可以調整;若Δ>0,則∑R2增加,該工作不能進行調整。同理,當該工作推遲nd時,資源變化量判別式如下[1]。

(5)

式中:k為累計推遲時間,R(j+n)為該非關鍵工作在第j+n天的資源需求量,R(i+n-1)為該非關鍵工作在第i+n-1天的資源需求量,tmn為該非關鍵工作的持續時間,T1為總推遲時間。

2 非關鍵工序組

非關鍵工序組定義為初始總時差相等的非關鍵工序的集合。按工序總時差的大小,將非關鍵工序分組,同一組內的工序,總時差相等,將單一非關鍵工序(即沒有與此工序總時差相同的工序)看成是只有一個工序的非關鍵工序組。將非關鍵工序組視為網絡圖中的1個獨立單位來進行資源均衡優化。非關鍵工序組優化判別式由姚玉玲 等[4]提出,由實例分析得判別公式。

ΔFGJ=REF+1-RES+1+R1≤0

(6)

式中:ES和EF分別為非關鍵工序組的最早開始時間和最早完成時間,R1為非關鍵工序組中第1個工作的資源需要量。此公式為非關鍵工序組移動1個單位時間的判別公式,將公式一般化得到非關鍵工序組移動n個單位時間的判別式。

Δ′=

(7)

式中:T1為推遲的總時間;n為推遲的單位時間;kmn為非關鍵工序mn推遲的累計時間;tmn為非關鍵工序mn持續時間;kmn-tmn為非關鍵工序mn被推遲天數與持續時間之差;Rmn為非關鍵工序mn上的資源需求量;REF+n為第EF+n天的資源需求量,RES+n為第ES+n天的資源需求量;∑(kmn-tmn)Rmn為該非關鍵工序組中每個kmn≤tmn的非關鍵工序的推遲時間和持續時間之差與其資源需求量之積的和。

3 最小方差法

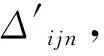
(8)

(9)

4 資源優化步驟

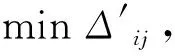
5 實例應用

圖1為雙代號時標網絡圖及某種資源需要量動態數列。假定時間單位為d。

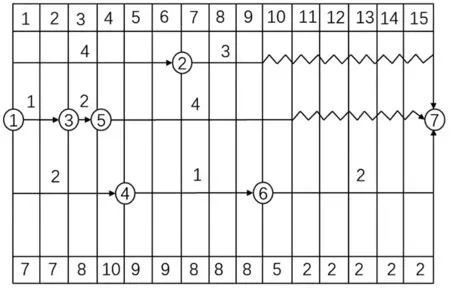
圖1 初始時標網絡圖及資源需求量

5.1 原始方法資源優化過程

5.1.1 第1次調整

在網絡圖中,利用時差進行調整的順序是自右向左逆箭線方向進行。當同一時間有多個工序擁有自由時差時,按單位時間資源需要量由大到小的順序進行調整。因此在圖1中,先考慮工序5→7的移動。

計算Δ′,計算式參考式(4)、(5)。

①R(10+1)-R(3+1)+R57=2-10+4=-4<0,可右移1 d。

②R(10+2)-R(3+2)+R57=2-9+4=-3<0,可右移1 d,共2 d。

③R(10+3)-R(3+3)+R57=2-9+4=-3<0,可右移1 d,共3 d。

④R(10+4)-R(3+4)+R57=2-8+4=-2<0,可右移1 d,共4 d。

⑤R(10+5)-R(3+5)+R57=2-8+4=-2<0,可右移1 d,共5 d。

由于自由時差已全部用完,且所有Δ′均小于等于0,所以5→7工序一共可以移動5 d。

5.1.2 第2次調整

由于工序2→7自由時差存在最后,所以考慮工序2→7的移動。

計算Δ′,計算式參考式(4)、(5)。

①R(9+1)-R(6+1)+R27=-2+3=1>0,不可移動1 d。

考察工序2→7是否可以移動2 d,3 d,…,6 d。

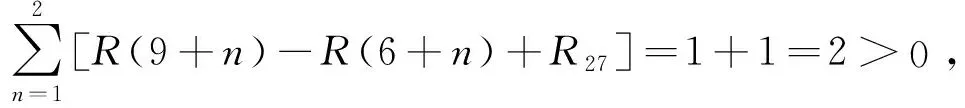
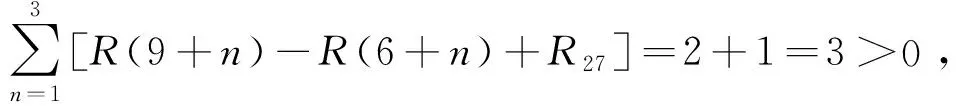
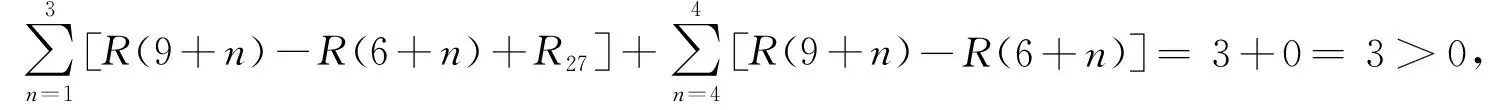
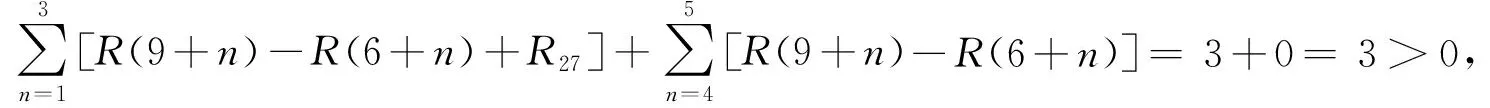
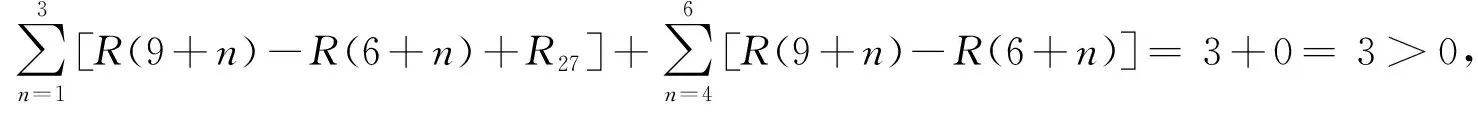
由上述計算知,工序2→7不可向右移動,所以以下考慮工序3→5的調整。

計算Δ′,計算式參考式(4)、(5)。

①R(3+1)-R(2+1)+R35=6-8+2=0,可向右移動1 d。

②R(3+2)-R(2+2)=5-6=-1<0,可向右移動1 d,共2 d。

③R(3+3)-R(2+3)=5-5=0,可向右移動1 d,共3 d。

④R(3+4)-R(2+4)=4-5=-1,可向右移動1 d,共4 d。

⑤R(3+5)-R(2+5)=4-4=0,可向右移動1 d,共5 d。

由上述式子可知,工序3→5可向右移動5 d,資源得到更均衡的分配,現對1→3工作進行調整。

5.1.3 第3次調整

計算Δ′,計算式參考式(4)、(5)。

①R(2+1)-R(0+1)+R13=6-7+1=0,可向右移動1 d。

②R(2+2)-R(0+2)+R13=6-7+1=0,可向右移動1 d,共2 d。

③R(2+3)-R(0+3)=5-6=-1<0,可向右移動1 d,共3 d。

④R(2+4)-R(0+4)=5-6=-1<0,可向右移動1 d,共4 d。

⑤R(2+5)-R(0+5)=4-5=-1<0,可向右移動1 d,共5 d。

由上述計算結果可知,工序1→3一共可向右移動5 d。資源得到更均衡分配,所有可調整箭線均已調整完成,優化結束,圖2為最后優化結果。

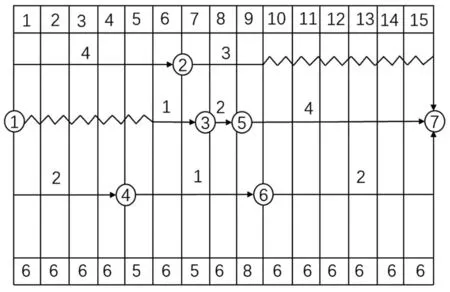
圖2 第3次調整網絡圖及資源需求量

5.2 優化方法過程(1次調整)

1)確定非關鍵線路組。圖1中非關鍵線路1→2→7的總時差相等都為6;非關鍵線路1→3→5→7的總時差相等都為6;所以令1→2→7為一個非關鍵線路組,1→3→5→7為一個非關鍵線路組。

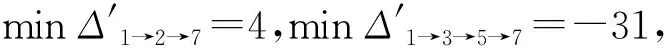
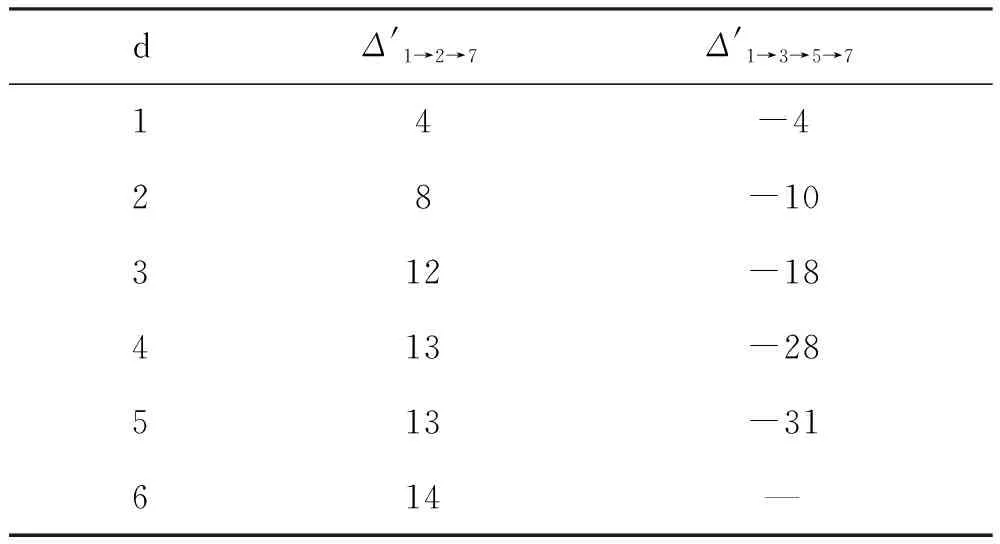
表1 非關鍵工序組移動后的方差變化值

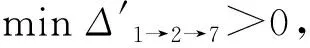
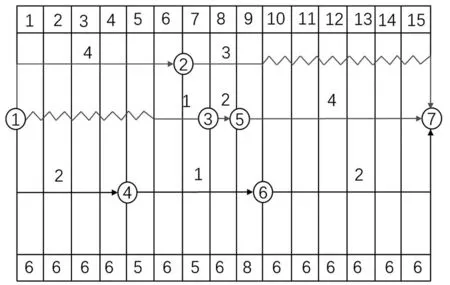
圖3 第1次調整后時標網絡圖及資源需求量

6 結論

改進后的縮方差法其實質就是將原優化過程許多中間環節進行合并、化簡。例如引入的非關鍵工序組方法,將多個可一起移動的非關鍵工序合并進行一起調整,減少了計算的工作量,從而使網絡計劃資源均衡優化模型得到進一步的完善。引入的最小方差法,針對同一節點有多個非關鍵工序組進行調整,將方差最小(即對應使資源配置最接近均衡的情況)值對應的移動時間作為調整時間,使資源配置盡可能一次性達到最優。本文更正并完善了縮方差法的判別公式,整合非關鍵工序組、最小方差法等方法使調優過程變得更加精簡,并減少了大量的計算和調整過程。從實例可以得出結論:原始縮方差法需要3次優化調整的資源,改進后的方法只需要1次即可完成,效率提升了近70%。證明了改進后的方法是切實有效的。