在探索規律中滲透學習方法
杜永寧
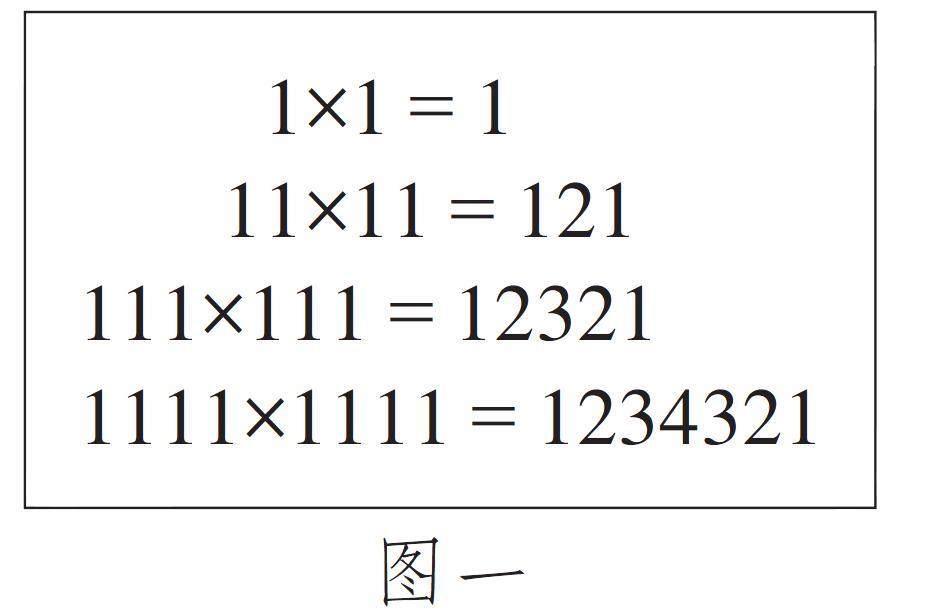

義務教育教科書西南師大版數學四(上)第七單元“三位數除以兩位數”安排了一個小節“探索規律”,其中例題1是用計算器計算,然后說說從下圖一的算式中,你發現了什么規律。并根據上面的規律,寫出11111×11111的積。
教學時,我在學生發現算式的規律后,要求他們直接寫出從5個1組合的數相乘到9個1組合的數相乘的積。完成后我們一起小結探索規律的過程:簡單(發現規律)→復雜(運用規律)。然后拋出一個問題:你能直接寫出222222222×555555555的積嗎?
學生在小組里討論,交流。時間一秒一秒,一分一分地流去……3分鐘還沒有思路。我叫停,與學生對話:這個問題復雜嗎?學生回答:很復雜。要得到答案我們現在最需要什么?發現這樣的特征的數相乘的積的規律。怎么去發現規律呢?學生看板書“簡單(發現規律)”。那為什么不從簡單的題目入手去發現呢?刷刷刷……嘀嘀嘀……學生記錄下2×5=10,22×55=1210,222×5555=123210,2222×5555=12343210。手舉起來了,爭先恐后要來寫222222222×555555555的得數,感覺這根本就不是個難題。完成后再小結:簡單(發現規律)→復雜(運用規律),遇到復雜的問題時,需要從簡單的情況入手去發現規律。
到此時,還沒有完。我請學生把這個題目與例題對比,看看你發現了什么。學生又有了驚喜(如圖二)。
感嘆,原來化復雜為簡單還可以這樣想——已經被發現的規律都是簡單的,可以作為思考的源泉。在這個過程中,學生還收獲了“積的變化規律”,算是例題目標之外,卻在教學設計之中。
我國數學家華羅庚指出,善于“退”,足夠地“退”,“退”到最原始而不失去重要性的地方,是學好數學的一個訣竅。在教學探索規律這種需要集中思考力的課堂里,我們要善于利用例題、擴展例題、改造例題,巧妙地滲透思考的方法、學習的方法,讓數學課生動而有力量。

