非均質物理雙擺的混沌特性研究

孔令輝 劉丁楊 蹇開林

摘要：為了解決工程實際中材料質量不均勻分布對雙擺系統運動的影響，在均質物理雙擺模型的基礎上，將擺的質心位置和擺的轉動慣量提取為變量，建立非均質雙擺模型。將非均質雙擺系統由Hamilton系統近似為擬Hamilton系統，運用雙自由度的Melnikov法，得到擬Hamilton系統存在Smale馬蹄意義下混沌的能量閾值，以此作為Hamilton系統的混沌條件。利用最大Lyapunov指數圖、分岔圖、Poincaré截面圖等數值方法驗證混沌條件的正確性，并詳細分析了各參數對系統運動狀態的影響和作用機制。結果表明，非均質雙擺的混沌閾值有較高復雜性，而且擺長、擺重、第一擺的質心位置同時影響著系統的能量與混沌閾值，解釋了質心位置和轉動慣量等參數發生變化時，系統在混沌和擬周期之間交替變換的原因。進一步研究了參數取值與Melnikov法適用性之間的關系，通過數值仿真分類討論了Melnikov法不適用時的參數取值情況。

關鍵詞：非均質物理雙擺；混沌；擬周期；Melnikov法

中圖分類號：O322????????? 文獻標志碼：A????? 文章編號：1000-582X（2024）02-106-13

Study on chaotic characteristics of heterogeneous physical double pendulum

KONG Linghui1a， LIU Dingyang2， JIAN Kailin1a，1b

（1a. School of Aeronautics and Astronautics; 1b. Chongqing Key Laobratory of Heterogenous Materisal Mechanics， Chongqing University， Chongqing 400044， P. R. China; 2. CSSC Haizhuang Windpower Co.， Ltd.， Chongqing 401122， P. R. China）

Abstract： To address the impact of materials with uneven mass distribution on the motion of double pendulum systems in engineering practice， a heterogeneous double pendulum model was established based on the homogeneous physical double pendulum model. This model incorporated variables， such as the position of the center of mass and the moment of inertia of the pendulum. To further explore the chaotic characteristics of the system， the heterogeneous double pendulum system was approximated from a Hamilton system to a quasi-Hamilton system. The dynamics equation of the double pendulum system was obtained using the Euler-Lagrange equation of the second kind. The energy threshold for Smale horseshoe chaos in the quasi-Hamiltonian system was determined using Melnikov method with two degrees of freedom， serving as the chaos condition for the Hamiltonian system. Through programming in Matlab， the correctness of the chaos condition was verified using numerical methods such as maximum Lyapunov exponential diagram， bifurcation diagram and Poincare section diagram. The influence of each parameter on the systems motion state and action mechanism was analyzed in detail. The results show that the chaos threshold of heterogeneous double pendulums depends on various factors， including the initial energy of the double pendulums， the position of the center of mass of the first pendulums and the ratio of the moment of inertia of the two pendulums. With different values for each parameter， the system changes from a regular motion state with a chaos threshold to an irregular and complex motion state without a chaos threshold. The reasons for the system alternating between chaotic and quasi-periodic states were explained， and theoretical predictions were validated. The differences between the theoretical threshold and actual numerical simulation results were explained when the center of mass of the first pendulum， the mass ratio of the two pendulums， and the ratio of moment of inertia of the two pendulums were set to their limit values. On this basis， the relationship between parameter values and the applicability of Melnikov method were further explored， and the parameters under which Melnikov method was no longer applicable were discussed by numerical simulation classification.

Keywords： heterogeneous physical double pendulum; chaos; quasi-period; Melnikov method

雙擺廣泛地應用于生活、工程與科學中。生活中，人的身體擺動[1]、高爾夫球揮桿[2]與網球揮拍[3]等常見動作以及工程上的機械臂[4]、機械足[5]、各種類型的起重機[6?8]、隔振器[9]、能量收集裝置[10]都可以簡化為雙擺模型。在科學上，范洪義等[11]通過擺、小車和彈簧的互相牽制效應研究了量子糾纏的經典類比問題。陳漢軍等[12]通過對雙物理擺混沌結果的研究，給一種新型振動機的參數設計提供了理論依據。Ford等[13]相信雙擺作為一個簡單的二自由度模型，很適用于測試量子力學能否描述經典混沌系統的觀測實驗，對經典混沌的量子對應研究意義重大。因此，雙擺的混沌問題備受關注。

Stachowiak等[14]通過Poincaré截面圖研究平面數學雙擺，研究表明系統的運動狀態與能量密切相關，在零能量極限時，雙擺做周期運動，隨著能量的增加，雙擺將從周期運動轉變為準周期運動，進而轉變為混沌運動。趙武等[15]、劉丁楊等[16]和Han等[17]應用Melnikov法研究了不同復雜擺系統的混沌閾值，并通過數值模擬加以驗證。Maiti等[18]研究了旋轉雙擺的混沌特性，發現系統的內共振將導致混沌。Bi等[19]使用Normal Form理論分析了自治雙擺系統在1：1內共振時的分岔特性，研究表明當存在周期激勵時，系統會按周期倍化的道路通向混沌；沒有周期激勵時，參數的改變也會影響其解的穩定性。Martynyuk等[20]利用動態對稱原理分析對雙擺產生混沌運動的條件，證明了雙擺質量比較大時，雙擺存在有條件的周期性軌跡和混沌軌跡。Calv?o等[21]不僅比較了分岔圖、最大Lyapunov指數譜圖、功率譜圖、傅里葉變換圖、時間歷程圖等不同方法在混沌研究中的優缺點，而且研究了兩擺初始角度對雙擺混沌的影響。Oiwa等[22]通過Kosambi-Cartan-Chern理論研究了雙擺的雅可比穩定性，給出了雅可比穩定性條件，通過Lyapunov指數和Poincaré截面圖，發現雅可比不穩定區域與混沌行為的開始有關。Kovacic等[23]研究了物理雙擺在低能級時的非線性正則模態，通過諧波平衡法和Lindstedt-Poincaré法分析了系統非線性振動的情況，結合數值仿真比較2種方法在不同情況下的優缺點。Dudkowski等[24]通過數值方法和實驗研究了具有參數激勵的機械雙擺，研究表明系統不規則運動的距離對參數和初始條件都非常敏感，而動態響應的特性嚴格依賴于激勵參數。

綜上所述，對于雙擺大都集中在采用Lyapunov指數、分岔圖和Poincaré圖等數值方法研究系統的混沌性，一部分理論是在研究雙擺穩定性之后，再考慮系統穩定性和混沌性的關系，少有對雙擺混沌性的理論研究以及能判斷系統出現混沌的理論閾值的研究。筆者考慮實際工程中材料非均質的特點，建立非均質物理雙擺模型，應用二自由度Melnikov法[25]研究非均質雙擺系統的混沌性質，從理論上得到系統的混沌閾值，更加深入地探究雙擺轉動慣量對混沌閾值的影響，揭示雙擺系統在各參數變化下誘發能量改變來對系統運動狀態產生的影響，并通過數值方法驗證其正確性。

1 非均質物理雙擺的動力學方程

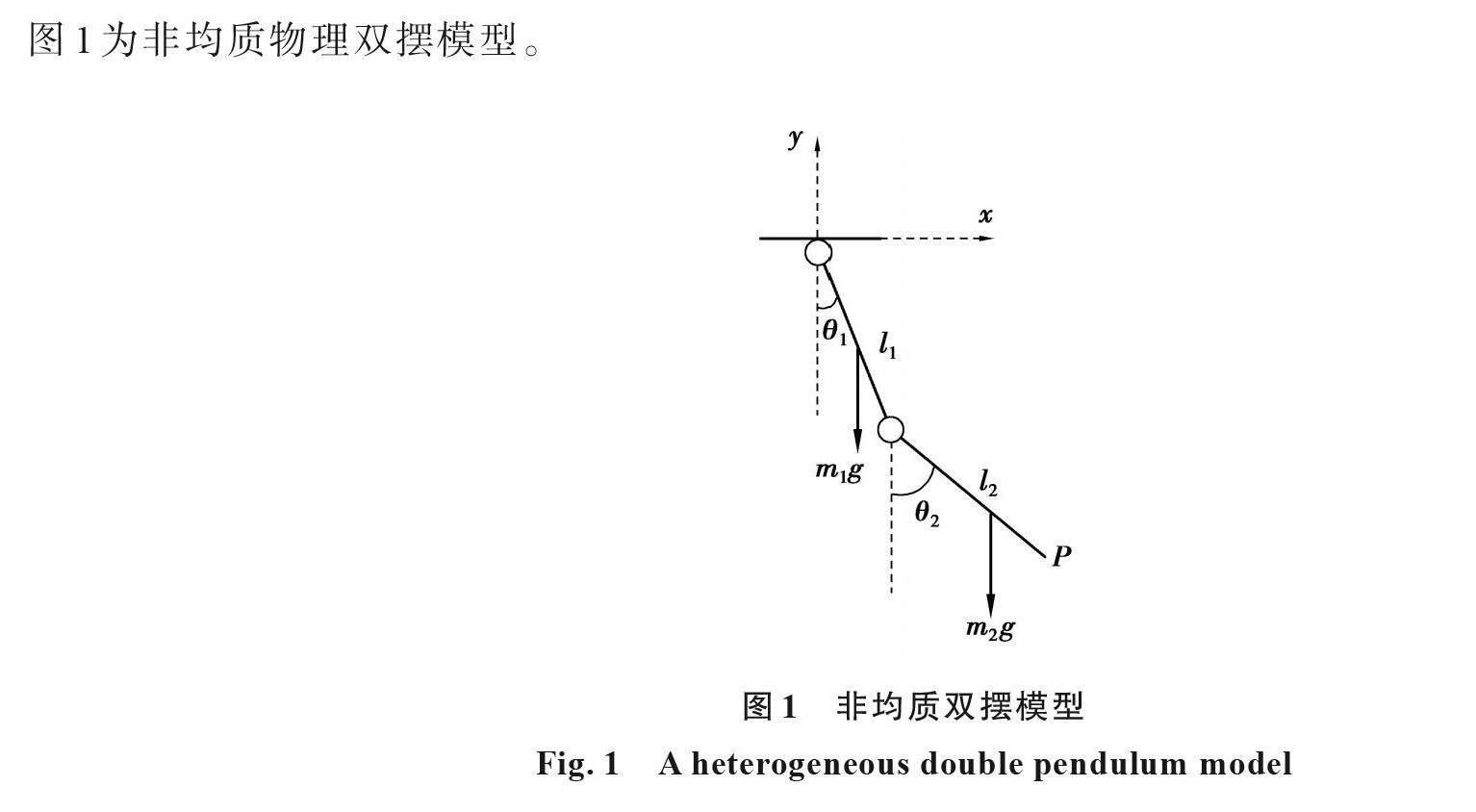
圖1為非均質物理雙擺模型。

該模型僅由2桿連接而成，假設2桿為剛性非均質直桿，建立如圖1所示的平面直角坐標系，記第二擺端點為P點，其坐標表示為（x，y）；2桿與豎直面的夾角為θ1、θ2，2桿角速度為θ ˙_1、θ ˙_2；桿長分別為l1、l2，假定鉸接處到質心的距離分別為l_1/k_1? 、 l_2/k_2 ，其中（k1，k2）∈（1，+∞）；質量大小分別為m1、m2，繞質心軸的轉動慣量分別為J1、J2；取重力加速度g=9.81 m/s2，其余參數的單位與g的單位相一致，系統總動能為

T=1/2 （m_1/（k_1^2 ）+m_2 ） l_1^2 θ ˙_1^2+1/2 J_1 θ ˙_1^2+1/2 J_2 θ ˙_2^2+1/2 m_2 [（l_2^2）/（k_2^2 ） θ ˙_2^2+（2l_1 l_2 θ ˙_1^? θ ˙_2^ ）/k_2? cos（θ_1-θ_2 ） ] 。?? （1）

系統總勢能為

V=（m_1/k_1 +m_2 ）gl_1 （1-cosθ_1 ）+1/k_2? m_2 gl_2 （1-cosθ_2 ） 。??? （2）

Euler-Lagrange第二類方程為

d/dt （（?L_g）/（?θ ˙_j^? ））-（?L_g）/（?θ_j ）=0， （3）

式中，L_g=T-V，因此，由式（3）得非均質物理雙擺的微分方程組

{（（m_1/（k_1^2 ）+m_2 ） l_1^2 θ ¨_1^ +（m_1/k_1 +m_2 ）gl_1 sinθ_1+J_1 θ ¨_1+（m_2 l_1 l_2）/k_2? [θ ¨_2 cos（θ_1-θ_2 ）+θ ˙_2^2 sin（θ_1-θ_2 ） ]=0，@（m_2 l_2^2）/（k_2^2 ） θ ¨_2+1/k_2? m_2 gl_2 sinθ_2+J_2 θ ¨_2+（m_2 l_1 l_2）/k_2? [θ ¨_1 cos（θ_1-θ_2 ）-θ ˙_1^2 sin（θ_1-θ_2 ） ]=0 。）┤???? （4）

將式（4）化為一階微分方程組，并令m_1/m_2 =m， l_1/k_1 =L_1， l_2/k_2 =L_2， L_1/L_2 =L， （J_1 k_1^2）/（m_1 l_1^2 ）=a， （J_2 k_2^2）/（m_2 l_2^2 ）=b，則式（4）可以改寫為式（5）。

{（θ ˙_1=w_1 "" ，@θ ˙_2=w_2 "" ，@w ˙_1=（（1+b）[L_2 sin（θ_1-θ_2 ） w_2^2+（1+m/k_1 ）gsinθ_1 ]+cos（θ_1-θ_2 ）[k_1 L_1 sin（θ_1-θ_2 ） w_1^2-gsinθ_2 ]）/（L_1 {k_1 cos^2 （θ_1-θ_2 ）-（1+b）[（a+1）m/k_1 +k_1 ] } ），@w ˙_2=（[（a+1）m/（k_1^2 ）+1]（gsinθ_2-k_1 L_1 sin（θ_1-θ_2 ） w_1^2 ）-cos（θ_1-θ_2 ）[L_2 sin（θ_1-θ_2 ） w_2^2+（1+m/k_1 ）gsinθ_1 ]）/（L_2 {cos^2 （θ_1-θ_2 ）-（1+b）[（a+1）m/（k_1^2 ）+1] } ） 。）┤???? （5）

2 Melnikov法分析非均質物理雙擺

Melnikov法是通過構建擬Hamilton系統的Melnikov函數來獲取系統混沌閾值的解析方法。雙擺系統的Hamilton函數就是系統的機械能函數，則雙擺系統的Hamilton函數H可以表示為式（6）。

（H=1/2 （m_1/（k_1^2 ）+m_2 ） l_1^2 θ ˙_1^2+1/2 m_2 （（l_2^2）/（k_2^2 ） θ ˙_2^2+（2l_1 l_2 θ ˙_1 θ ˙_2）/k_2? cos（θ_1-θ_2 ） ）+@?????? 1/2 J_1 θ ˙_1^2+1/2 J_2 θ ˙_2^2+1/k_2? m_2 gl_2 （1-cosθ_2 ）+（m_1/k_1 +m_2 ）gl_1 （1-cosθ_1 ）。）?? （6）

對式（6）中的余弦項cos（θ_1-θ_2 ）進行放縮處理，取cos（θ_1-θ_2 ）/（k_2 g）為ε_1；對cosθ_2進行泰勒展開有cosθ_2=1-（θ_2^2）/2！+cosξ/4！ θ_2^4，取Lagrange余項的常數項cos（ξ）/24 （0<ξ<θ_2 ）為ε_2，因此式（6）化為式（7）。

（H=1/2 （m_1/（k_1^2 ）+m_2 ） l_1^2 θ ˙_1^2+1/2 J_1 θ ˙_1^2+1/2 J_2 θ ˙_2^2+1/k_2? m_2 gl_2 （1/2 θ_2^2-ε_2 θ_2^4 ）+@?????? 1/2 m_2 （（l_2^2）/（k_2^2 ） θ ˙_2^2+2ε_1 l_1 l_2 gθ ˙_1 θ ˙_2 ）+（m_1/k_1 +m_2 ）gl_1 （1-cosθ_1 ），）?? （7）

式中，ε_1 、ε_2都遠小于1，可以看作微小擾動，且ε_1 、ε_2數值上相差不大，為方便計算，統一用ε代替。因此，擬Hamilton系統能量函數H^e可整理為兩相平面函數F1（θ1，θ ˙_1）、F2（θ2，θ ˙_2）與微擾函數H^'的和，如式（8）所示。

{（H^e=F_1 （θ_1，θ ˙_1 ）+F_2 （θ_2，θ ˙_2 ）+εH^'，@F_1 （θ_1，θ ˙_1 ）=1/2 （m_1/（k_1^2 ）+m_2 ） l_1^2 θ ˙_1^2+1/2 J_1 θ ˙_1^2+（m_1/k_1 +m_2 ）gl_1 （1-cosθ_1 ），@F_2 （θ_2，θ ˙_2 ）=1/2? （m_2 l_2^2）/（k_2^2 ） θ ˙_2^2+1/2? （m_2 gl_2）/k_2? θ_2^2+1/2 J_2 θ ˙_2^2，@H^'=m_2 l_1 l_2 gθ ˙_1 θ ˙_2-1/k_2? m_2 gl_2 θ_2^4 。）┤? （8）

由F1（θ1，θ ˙_1）可知，相平面（θ1，θ ˙_1）存在中心（0，0），在θ_1∈（-2π，2π）上有雙曲鞍點（-π，0）（π，0），存在2條經過2點的異宿軌道，將（-π，0）（π，0）代入F1（θ1，θ ˙_1）得對應的Hamilton量為h_1=2（m_1/k_1 +m_2 ）gl_1。

引入變量（I，t），做如式（9）的變換（θ2，θ ˙_2）?（I，t）。將式（9）分別代入式（8）的F2（θ2，θ ˙_2）和H'中，得到式（10），可見相平面（θ2，θ ˙_2）中僅存在以I為參數的周期軌道。

{（θ_2=√（（2k_2 I）/（m_2 l_2 g） √（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）））? sin（√（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）） t），@θ ˙_2=√（（2k_2^2 I）/（m_2 l_2^2+k_2^2 J_2 ） √（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）））? cos（√（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）） t），）┤ （9）

{（F_2 （θ_2，θ ˙_2 ）=G（I）=√（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）） I ，@H^'=m_2 l_1 l_2 k_2 gθ ˙_1 √（2I/（m_2 l_2^2+k_2^2 J_2 ） √（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ））） ?cos（√（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）） t）-（4k_2^2 I^2）/（m_2 l_2^2+k_2^2 J_2 ） sin^4 （√（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）） t）。）┤???? （10）

若令1-cosθ_1=1/2 θ_1^2-1/24 θ_1^4+o（θ_1^6 ），略去Peano余項后代入式（8）中的F1（θ1，θ ˙_1），則（θ1，θ ˙_1）上的異宿軌道參數化為

{（θ_10=±√6 tanh（√（（（m_1 k_1+m_2 k_1^2 ）gl_1）/2（（m_1+m_2 k_1^2 ） l_1^2+J_1 k_1^2 ） ） t），@θ ˙_10=±√（（3（m_1 k_1+m_2 k_1^2 ）gl_1）/（（m_1+m_2 k_1^2 ） l_1^2+J_1 k_1^2 ）） sech^2 （√（（（m_1 k_1+m_2 k_1^2 ）gl_1）/2（（m_1+m_2 k_1^2 ） l_1^2+J_1 k_1^2 ） ） t）。）┤?? （11）

當系統的Hamilton量Hh_1時，相平面（θ1，θ ˙_1）上存在不穩定流形。穩定流形和不穩定流形之間的距離由Melnikov函數[26]表示，如式（12）所示。

（M_± （t_0 ）=∫_（-∞）^（+∞）?{F_1，H^' }? （t-t_0 ）dt=∫_（-∞）^（+∞）?∑_（i=1）^2?（（?F_1）/（?θ_i ）? （?H^'）/（?θ ˙_i ）-（?F_1）/（?θ ˙_i ）? （?H^'）/（?θ_i ））? （t-t_0 ）dt=@??????????????? ?2 （（m_1/k_1 +m_2）m_2^2 l_1 l_2^2 k_2^2 g^2 π）/（（m_2 l_2^2+k_2^2 J_2 ）^2 （m_1 k_1+m_2 k_1^2 ） ） （（m_1+m_2 k_1^2 ） l_1^2+J_1 k_1^2 ）?@???????????????? √（（6m_2 l_2 k_2 （h_1-2（m_1/k_1 +m_2 ）gl_1 ））/（（m_1 k_1+m_2 k_1^2 ） l_1 ）） √（（（m_1+m_2 k_1^2 ） l_1^2+J_1 k_1^2 ） ）?@???????????????? csch（√（（m_2 l_2 k_2 （（m_1+m_2 k_1^2 ） l_1^2+J_1 k_1^2 ））/（2（m_1 k_1+m_2 k_1^2 ） l_1 （m_2 l_2^2+k_2^2 J_2 ） ）） π）sin（√（（m_2 l_2 k_2 g）/（m_2 l_2^2+k_2^2 J_2 ）） t_0 ）。）????? （12）

由式（12）可知，Melnikov函數為振蕩型，存在簡單零點，則Poincaré映射存在橫截異宿點，由Smale-Birkhoff同宿定理可知，系統存在Smale馬蹄意義下的混沌。綜上可知，當ε充分小時，擬Hamilton系統在H≥2（m_1/k_1 +m_2 ）gl_1的能量條件下存在橫截異宿點，系統將呈現混沌的性質。擬Hamilton系統在相平面（θ2，θ ˙_2）上沒有不穩定流形，也就不存在橫截異宿點，因此只需討論存在不穩定流形的相平面（θ1，θ ˙_1）。而對于Hamilton系統，相平面（θ2，θ ˙_2）上的相軌道并非純粹的周期軌道，可能存在不穩定流形；不略去Peano余項，F1（θ1，θ ˙_1）也無法參數化，這些因素或多或少會影響系統的混沌性。但H≥2（m_1/k_1 +m_2 ）gl_1的混沌閾值依然有一定的預測作用。

前面是在相平面（θ1，θ ˙_1）上求得第1個混沌閾值。若對余弦項cosθ_1進行泰勒展開，做變換（θ1，θ ˙_1）?（I，t），重復上述步驟，也可以得到相似的結論：當ε充分小時，擬Hamilton系統在H≥2/k_2? m_2 gl_2的能量條件下存在橫截同宿點；對于Hamilton系統，在H<2/k_2? m_2 gl_2時也可能處于混沌狀態。對整個系統而言，無論在哪一相平面上，只要存在橫截同宿點就意味著系統處于混沌狀態，因此雙擺系統的理論混沌閾值H≥min{2（m_1/k_1 +m_2 ）gl_1，2/k_2? m_2 gl_2 }。

3 數值仿真驗證混沌條件

本節將通過數值方法討論雙擺系統理論混沌閾值的適用條件，并且θ_1、θ_2、θ ˙_1、θ ˙_2特指初始時刻的系統參數。

3.1 僅考慮動能的混沌條件數值模擬驗證

觀察Hamilton函數式與混沌條件H≥min{2（m_1/k_1 +m_2 ）gl_1，2/k_2? m_2 gl_2 }可知，雙擺系統的Hamilton量由（θ1，θ2，θ ˙_1，θ ˙_2，m1，m2，l1，l2）8個物理量構成，而混沌條件僅包含（m1，m2，l1，l2），因此可以推測，在（θ1，θ2，m1，m2，l1，l2）相同的參數條件下，（θ ˙_1，θ ˙_2）越大，越有可能超越混沌閾值。

為驗證上述推測，本節選取均質桿進行驗證，均質桿可以看作非均質桿取k_1=k_2=2，a=b=1/3的特殊情況，可以用來初步驗證所求閾值的正確性。以θ ˙_2為變量，取（θ1，θ2，θ ˙_1，m1，m2，l1，l2）=（0，0，0，1，1，1，1）代入混沌條件，可得閾值為θ ˙_2^2≥6g，即|θ ˙_2 |≥7.67，上述條件下，圖2為以θ ˙_2為分岔參數的分岔圖，可見當θ ˙_2=0時，系統始終靜止，因此分岔圖以（0，0）為中心；圖中正、負半軸近乎對稱，可見速度的方向并不會影響系統的狀態；在擺的質量確定的情況下，速度的大小決定動能的大小，也從側面反映能量才是決定系統混沌與否的關鍵。隨著|θ ˙_2 |不斷增大，分岔圖由清晰、連續的線轉變為模糊、離散的點，但無法確定具體的混沌閾值。圖3為上述條件下系統的Poincaré截面圖，|θ ˙_2 |=7.6時，Poincaré截面圖依然是封閉的曲線，表現出擬周期的特征；而|θ ˙_2 |=7.7時，Poincaré截面圖已經變為雜亂無序的點，顯現混沌的特征。圖4為|θ ˙_2 |=7.6和|θ ˙_2 |=7.7時的第二擺上P點運動軌跡圖，|θ ˙_2 |=7.6時運動軌跡有明顯的區域范圍，|θ ˙_2 |=7.7時運動軌跡則雜亂無序、十分復雜，說明由Melnikov法獲得的混沌閾值可靠。

3.2 僅考慮勢能的混沌條件數值模擬驗證

假定雙擺系統無初速度，同時考慮2（m_1/k_1 +m_2 ）gl_1和2/k_2? m_2 gl_2 2個閾值，有

{（H≥2（m_1/k_1 +m_2 ）gl_1@H≥2/k_2? m_2 gl_2 ）┤?{（（k_1+m_1/m_2 ）? （l_1 k_2）/（k_1 l_2 ）≤（1-cosθ_2）/（1+cosθ_1 ），@（k_1+m_1/m_2 ）? （l_1 k_2）/（k_1 l_2 ）≤（1+cosθ_2）/（1-cosθ_1 ） 。）┤? （13）

將式（13）簡化為式（14）

{（（k_1+m）L≤（1-cosθ_2）/（1+cosθ_1 ），@（k_1+m）L≥（1+cosθ_2）/（1-cosθ_1 ） 。）┤??? （14）

由式（14）可知，影響系統混沌的并非擺的總長l_1 、l_2，而是鉸接處到重心的長度L_1 、L_2；代表第一擺質心位置的k_1可以單獨對系統產生影響，而代表第二擺重心位置的k_2必須與l_2組合成L_2來影響系統，可見第一擺重心位置對系統混沌性的影響要大一些。隨角度參數θ_1 、θ_2的取值不同，會出現兩種假設情況，一是（1-cosθ_2）/（1+cosθ_1 ）≥（1+cosθ_2）/（1-cosθ_1 ），即cosθ_1+cosθ_2≤0，無論（k_1+m）L取何值，雙擺系統都為混沌運動；二是（1-cosθ_2）/（1+cosθ_1 ）<（1+cosθ_2）/（1-cosθ_1 ），即cosθ_1+cosθ_2>0，此時（k_1+m）L在某一范圍內，系統存在擬周期運動，其余為混沌運動。

3.2.1 完全混沌

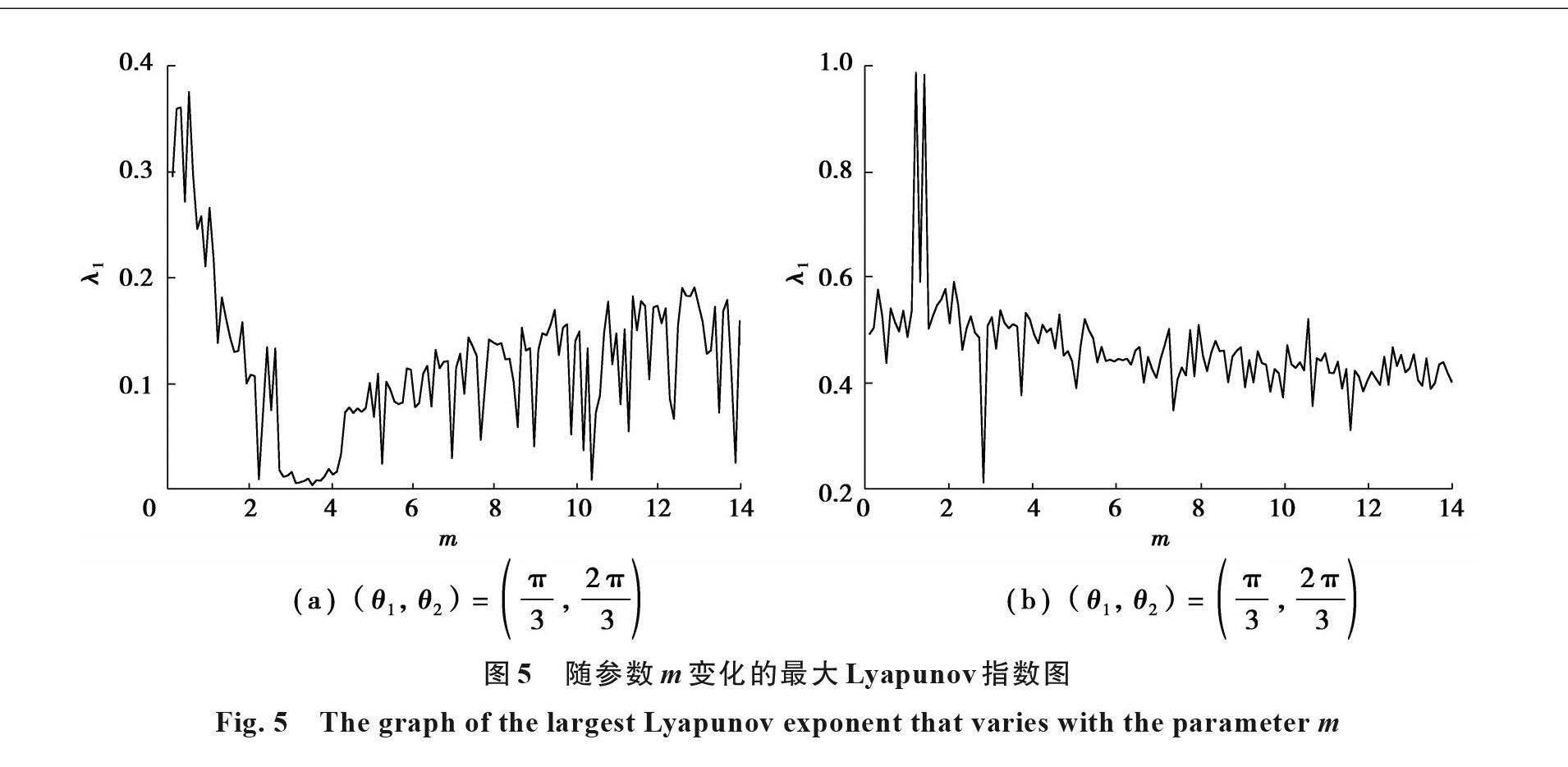
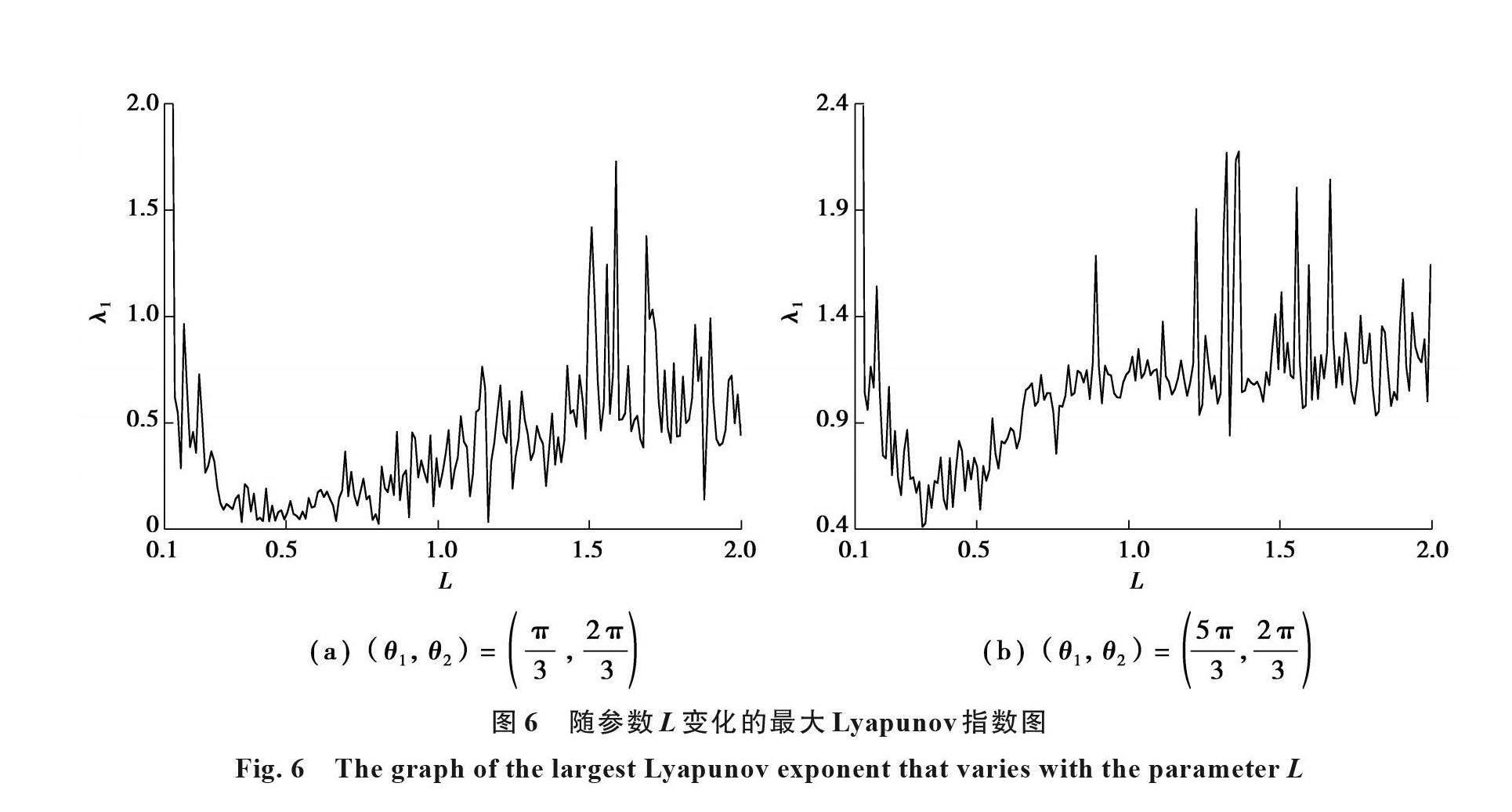
本節取（θ1，θ2）=（π/3，2π/3）和（θ1，θ2）=（5π/6，2π/3），此時無論（k1+m）L取何值，雙擺系統都應為混沌運動。同樣選擇均質物理雙擺系統進行分析，圖5為（θ ˙_1，θ ˙_2，L）=（0，0，2/9）時，隨參數m變化的最大Lyapunov指數圖，圖6為在（θ ˙_1，θ ˙_2，m）=（0，0，1）時，隨參數L變化的最大Lyapunov指數圖。最大Lyapunov指數也始終大于0，表明系統與理論推測相同，處于混沌運動。兩圖中（b）圖的Lyapunov指數顯然大于（a）圖的Lyapunov指數，表明在（b）圖的參數條件下，系統在相鄰相軌道間發散得更加嚴重，系統混沌程度更深。

3.2.2 局部擬周期

當（1-cosθ_2）/（1+cosθ_1 ）<（1+cosθ_2）/（1-cosθ_1 ）時，系統應存在擬周期運動，這里通過數值仿真，改變第一擺質心位置k_1與質量比m的取值來驗證理論閾值的正確性。取固定參數（θ1，θ2，θ ˙_1，θ ˙_2，L，a，b）=（π/3，π/2，0，0，2/9，1/3，1/3），圖7為在不同k1下，以m為分岔參數的分岔圖。圖7（a）中k1=1.4，圖中m≤1.48處離散點完全發散，說明系統在（m+k1）≤2.88的區域做混沌運動，略小于理論值；分岔圖在1.48≤m≤7處為十幾條清晰的線相互糾結在一起，系統做擬周期運動；在7≤m≤7.6處清晰的線逐漸轉變為離散點，但沒有發散，可見系統處于擬周期態到混沌態的過渡階段；在m=7.6處離散點第一次發散，可見系統在（m+k1）≥9時開始進行混沌運動，與理論相符合。圖7（b）中k1=1.7，圖中m≤1.5與m≥7.2處離散點完全發散，說明系統在（m+k1）≤3.2與（m+k1）≥8.9的區域做混沌運動，混沌區域略大于理論值。圖7（c）中k1=2，此即均質雙擺，圖中m≤1.55與m≥5.67處離散點完全發散，說明系統在（m+k1）≤3.55與（m+k1）≥7.67處做混沌運動，混沌區域雖略大于理論值，但在理論區域確實是做混沌運動。圖7（d）中k1=2.2，系統在（m+k1）≤3.8時做混沌運動，在（m+k1）≥7.2時出現離散點并開始向混沌態過渡，直到（m+k1）≥7.5時開始做混沌運動。

事實表明，當（1-cosθ_2）/（1+cosθ_1 ）<（1+cosθ_2）/（1-cosθ_1 ）時，系統存在擬周期態，且當擺的質心越接近擺尾，即k_1越小時，系統的擬周期運動區域越大。

4 模型局限性分析

4.1 k_1≈（1-cosθ_2）/（1+cosθ_1 ）L或k_1>（1-cosθ_2）/（1+cosθ_1 ）L

圖8為取參數（θ1，θ2，θ ˙_1，θ ˙_2，L，a，b）=（π/3，π/2，0，0，2/9，1/3，1/3）時以m為分岔參數的分岔圖，此時（1-cosθ_2）/（1+cosθ_1 ）L=3。圖8（a）中k1=2.8，按照理論計算，系統應在m≤0.2與m≥6.2的區域內做混沌運動，圖中0.06≤m≤0.2時系統做擬周期運動，與理論預測不符，但依然滿足m≥6.2的混沌條件。圖8（b）中k1=3.2，圖中5.8≤m≤6.93時系統做擬周期運動，與系統應在m≥5.8時做混沌運動不相符，說明第一擺質心位置的k_1在數值上接近（1-cosθ_2）/（1+cosθ_1 ）L時，理論閾值只能正確預測（k_1+m）L≥（1+cosθ_2）/（1-cosθ_1 ）的部分，當k_1超越（1-cosθ_2）/（1+cosθ_1 ）L時，理論閾值將完全不適用。

4.2 m_1?m_2

圖9為取參數（θ1，θ2，θ ˙_1，θ ˙_2，k1，a，b）=（π/3，π/2，0，0，2，1/3，1/3）時以m為分岔參數的分岔圖，該圖表明，若m較大時，在l_1?l_2的情況下，第一擺的能量占系統總能量的絕大部分，第二擺對系統的影響很小；而在l_2?l_1時，兩擺間難以產生較大的影響，此時可以將系統看作為1個單擺系統加上1個第二擺產生的微小擾動。因此，在這2種條件下系統在參數m較大的區域進行擬周期運動，而非混沌運動。

4.3 J_2?J_1或J_1?J_2

圖10為取參數（θ1，θ2，θ ˙_1，θ ˙_2，L，k1）=（π/3，π/2，0，0，2/9，1.7）時以m為分岔參數的分岔圖，在此參數條件下系統將在m≤1.3與m≥7.3的區域做混沌運動，此時J_1/J_2 =4am/81b。

當J_2?J_1即b?a時，如圖10（a）（b）中分別取（a，b）=（0.1，0.4）和（a，b）=（0.1，0.8），系統在0≤m≤10內由混沌態轉為擬周期態后，沒有再出現明確的混沌區閾值，表明當第二擺轉動慣量遠大于第一擺轉動慣量時，隨著雙擺質量比m的增加，系統將出現趨于穩定的擬周期運動，其原因是在雙擺運動過程中，轉動慣量會影響系統的動能，根據機械能守恒定理知，第二擺的轉動慣量越大，速度就會越小，此時可以把第二擺的運動看做在單擺系統上加一個微小的擾動，因此系統會趨于擬周期運動。

當J_2≈J_1時，如圖10（c）中取（a，b）=（0.3，0.3）時，系統在0≤m≤1.63時為混沌運動，在1.63≤m≤5.76時為擬周期運動，在5.76≤m≤10時為混沌運動，雖然實際混沌區域大于理論預測，但在理論預測的區域確實做混沌運動。如圖10（d）中取（a，b）=（0.6，0.3）時，系統在0≤m≤1.3時為混沌運動，在1.3≤m≤6.73時為擬周期運動，在6.73≤m≤10時為混沌運動，此時理論閾值具有很好的適用性。

當J_1?J_2時，如圖10（e）（f）中分別取（a，b）=（0.8，0.1）和（a，b）=（0.9，0.1），此時系統在0≤m≤10內作由混沌態轉變為擬周期態又轉變為混沌態的循環往復的運動。這說明當第一擺的轉動慣量遠大于第二擺的轉動慣量時，系統的運動將受到兩擺質量比的影響而出現極其復雜的運動。對比六次仿真結果可知，系統在運動過程中，轉動慣量會對系統的動能產生影響從而改變系統混沌條件，當兩擺的轉動慣量差距過大時，Melnikov法得出的能量閾值不再適用。

5 結? 論

建立了非均質物理雙擺運動的擬Hamilton模型，根據雙自由度的Melnikov法提出了擬Hamilton系統發生混沌的能量閾值，得到了一般情況下系統發生混沌的條件。通過改變雙擺模型中的質心位置、擺長比以及轉動慣量來體現雙擺非均質的特點，再根據不同參數下系統的分岔圖、Poincaré截面圖對理論閾值進行驗證，給出了模型的適用條件，并完成了局限性分析。基于本研究，可得出以下結論：

1）分析非均質物理雙擺混沌的理論閾值，發現影響系統混沌的并非雙擺的擺長l1、l2，而是雙擺質心到鉸接處的距離L1、L2，并且在雙擺質量和長度確定的情況下，L1、L2越大，系統發生混沌所需要的能量就越大。

2）分析雙擺質心位置對系統混沌特性的影響，發現第一擺的質心位置k1可以直接影響系統混沌特性，而第二擺的質心位置k2則不能單獨對系統的混沌特性產生影響。利用數值仿真改變k1的大小，從而進一步得到了第一擺質心位置對理論閾值的適用性，發現當k1在數值上接近（1-cosθ_2）/（1+cosθ_1 ）L時，理論閾值的適用性變差，當k1大于（1-cosθ_2）/（1+cosθ_1 ）L時，理論閾值將完全不適用。

3）分析雙擺轉動慣量對系統混沌特性的影響，發現雙擺通過轉動慣量的改變使得運動時動能發生改變，進而影響系統的混沌閾值，并且知道當第二擺的轉動慣量遠大于第一擺的轉動慣量時，系統將趨于擬周期運動；當第一擺的轉動慣量遠大于第二擺時，系統作混沌態、擬周期態循環往復的復雜運動；當雙擺的轉動慣量相似時，系統能很好地在理論閾值區域內做混沌運動。表明在極限條件下，理論閾值存在一定的局限。

4）非均質雙擺系統的混沌特性研究對類似系統的混沌抑制有著重要的啟示作用。具體來說，可以通過研究雙擺系統的混沌控制方法來抑制類似系統的混沌特性，實現系統的穩定控制。例如，對于機器人肩部和腿部的運動，通過控制雙擺系統的擺臂長度和擺錘重量比等參數，可以實現關節運動的控制和規劃。另外，在航空航天領域中，太陽能帆板的展開涉及到桿件和軸承的不確定性，容易導致非線性振動和失穩現象的發生，因此可以通過研究雙擺混沌控制方法來控制太陽能帆板的展開過程，實現太陽能帆板的準確展開。總之，通過研究非均質物理雙擺系統的混沌特性，在工程實際中可以針對類似系統的混沌特性進行控制和抑制，提高系統的穩定性和控制精度。

參考文獻

［1］? Petró B， Kiss B， Kiss R M. Analyzing human balance recovery action using calculated torques of a double pendulum model[J]. Materials Today： Proceedings， 2019， 12： 431-439.

［2］? Betzler N， Monk S， Wallace E， et al. From the double pendulum model to full-body simulation： evolution of golf swing modeling[J]. Sports Technology， 2008， 1（4/5）： 175-188.

［3］? Youn S H. Double pendulum model for a tennis stroke including a collision process[J]. Journal of the Korean Physical Society， 2015， 67（7）： 1110-1117.

［4］? Verduzco F， Alvarez J. Homoclinic chaos in 2-DOF robot manipulators driven by PD controllers[J]. Nonlinear Dynamics， 2000， 21（2）： 157-171.

［5］? 張紅巧， 田瑞蘭， 陳恩利， 等. 參數激勵下均質桿狀雙擺的周期穩定振動[J]. 振動與沖擊， 2020， 39（16）： 231-235.

Zhang H Q， Tian R L， Chen E L， et al. Periodically stable vibration of homogeneousrod-shaped double pendulum under parametric excitation[J]. Journal of Vibration and Shock， 2020， 39（16）： 231-235.（in Chinese）

［6］? Shi H T， Yao F X， Yuan Z， et al. Research on nonlinear coupled tracking controller for double pendulum gantry cranes with load hoisting/lowering[J]. Nonlinear Dynamics， 2022， 108（1）： 223-238.

［7］? Sun N， Wu Y M， Chen H， et al. An energy-optimal solution for transportation control of cranes with double pendulum dynamics： design and experiments[J]. Mechanical Systems and Signal Processing， 2018， 102： 87-101.

［8］? Zhang M H， Ma X， Chai H， et al. A novel online motion planning method for double-pendulum overhead cranes[J]. Nonlinear Dynamics， 2016， 85（2）： 1079-1090.

［9］? Kumar R， Gupta S， Ali S F. Energy harvesting from chaos in base excited double pendulum[J]. Mechanical Systems and Signal Processing， 2019， 124： 49-64.

［10］? 王觀， 胡華， 伍康， 等. 基于兩級擺桿結構的超低頻垂直隔振系統[J]. 物理學報， 2016， 65（20）： 200702.

Wang G， Hu H， Wu K， et al. Ultra-low-frequency vertical vibration isolator based on a two-stage beam structure[J]. Acta Physica Sinica， 2016， 65（20）： 200702.（in Chinese）

［11］? 范洪義， 吳澤. 介觀電路中量子糾纏的經典對應[J]. 物理學報， 2022， 71（1）： 010302.

Fan H Y， Wu Z. Classical correspondence of quantum entanglement in mesoscopic circuit[J]. Acta Physica Sinica， 2022， 71（1）： 010302.（in Chinese）

［12］? 陳漢軍， 黃東衛， 蘇永福. 雙物理擺的混沌分析[J]. 數學的實踐與認識， 2007， 37（15）： 49-53.

Chen H J， Huang D W， Su Y F. Chaos analysis of the double-body pendulum[J]. Mathematics in Practice and Theory， 2007， 37（15）： 49-53.（in Chinese）

［13］? Ford J， Ilg M. Eigenfunctions， eigenvalues， and time evolution of finite， bounded， undriven， quantum systems are not chaotic[J]. Physical Review A， 1992， 45（9）： 6165-6173.

［14］? Stachowiak T， Okada T. A numerical analysis of chaos in the double pendulum[J]. Chaos， Solitons & Fractals， 2006， 29（2）： 417-422.

［15］? 趙武， 張鴻斌， 孫超凡， 等. 受垂直激勵和水平約束的單擺系統亞諧共振分岔與混沌[J]. 物理學報， 2021， 70（24）： 240202.

Zhao W， Zhang H B， Sun C F， et al. Subharmonic resonance bifurcation and chaos of simple pendulum system with vertical excitation and horizontal constraint[J]. Acta Physica Sinica， 2021， 70（24）： 240202.（in Chinese）

［16］? 劉丁楊， 蹇開林， 張亮. 基于Melnikov法的雙擺系統混沌特性研究[J]. 振動與沖擊， 2022， 41（14）： 92-98.

Liu D Y， Jian K L， Zhang L. Chaotic characteristics of a double pendulum system based on the Melnikov method[J]. Journal of Vibration and Shock， 2022， 41（14）： 92-98.（in Chinese）

［17］? Han N， Lu P P. Nonlinear dynamics of a classical rotating pendulum system with multiple excitations[J]. Chinese Physics B， 2020， 29（11）： 110502.

［18］? Maiti S， Roy J， Mallik A K， et al. Nonlinear dynamics of a rotating double pendulum[J]. Physics Letters A， 2016， 380（3）： 408-412.

［19］? Bi Q S， Chen Y S. Bifurcation analysis of a double pendulum with internal resonance[J]. Applied Mathematics and Mechanics， 2000， 21（3）： 255-264.

［20］? Martynyuk A A， Nikitina N V. The theory of motion of a double mathematical pendulum[J]. International Applied Mechanics， 2000， 36（9）： 1252-1258.

［21］? Calv?o A M， Penna T P. The double pendulum： a numerical study[J]. European Journal of Physics， 2015， 36（4）： 045018.

［22］? Oiwa S， Yajima T. Jacobi stability analysis and chaotic behavior of nonlinear double pendulum[J]. International Journal of Geometric Methods in Modern Physics， 2017， 14（12）： 1750176.

［23］? Kovacic I， Zukovic M， Radomirovic D. Normal modes of a double pendulum at low energy levels[J]. Nonlinear Dynamics， 2020， 99（3）： 1893-1908.

［24］? Dudkowski D， Wojewoda J， Czo?czyński K， et al. Is it really chaos？ The complexity of transient dynamics of double pendula[J]. Nonlinear Dynamics， 2020， 102（2）： 759-770.

［25］? 李繼彬， 陳鳳娟. 混沌、Melnikov方法及新發展[M]. 北京： 科學出版社， 2012.

Li J B， Chen F J. Chaos， Melnikov method and its new development[M]. Beijing： Science Press， 2012.（in Chinese）

［26］? Holmes P J， Marsden J E. Horseshoes in perturbations of Hamiltonian systems with two degrees of freedom[J]. Communications in Mathematical Physics， 1982， 82（4）： 523-544.

（編輯? 鄭潔）