具有無癥狀感染的新冠病毒傳播模型研究

原玉茹 李淑萍

摘? 要：為研究無癥狀感染者對新冠病毒的傳播影響，建立了一個具有無癥狀感染的新冠病毒傳播動力學模型.首先，利用下一代矩陣法求得基本再生數R0.其次，當R0＜1時，應用Hurwitz判據證明了無病平衡點的局部穩定性，并通過構造Lyapunov函數的方法證明了無病平衡點的全局穩定性；當R0＞1時，系統存在唯一的地方病平衡點且是局部漸近穩定的，并證明了系統的一致持續性.然后，利用最優控制理論，求得了最優控制解的表達形式.最后，通過數值模擬驗證了理論結果，并對參數進行敏感性分析，說明無癥狀感染者對新冠病毒傳播的影響程度不容忽視，應采取居家隔離措施來降低疾病的傳播率.

關鍵詞：無癥狀感染；穩定性；一致持續；最優控制；敏感性分析

中圖分類號：O175.1????? 文獻標志碼：A文章編號：1000-2367（2024）03-0071-09

傳染病是人類生存的最大威脅之一，傳染病的反復流行，不僅影響人類的身體健康，更大程度上損害了社會利益，因此流行病學和其他生物學領域的研究人員開始了解傳染病并嘗試通過模型的研究來揭示疾病的流行規律，預測流行趨勢，為發現、預防和控制疾病的流行提供理論根據和策略.從2019年末起，由嚴重急性呼吸綜合征冠狀病毒2（severe acute respiratory syndrome coronavirus 2，SARS-CoV-2）引起的新型冠狀病毒感染在中國和世界各地蔓延.該病毒的癥狀表現為干咳、發燒和疲勞，進一步還可能導致肺炎、腎衰竭甚至死亡［1-4］.這種病毒可以通過身體接觸、打噴嚏和咳嗽時的飛沫在人與人之間傳播，并且越來越多的證據表明，新冠病毒的快速傳播在一定程度上是由無癥狀感染者驅動的.

無癥狀感染者是一類具有傳染性但是沒有相關臨床癥狀的群體，他們隱藏在人群中不容易被發現，因此在病毒的傳播過程中，這類群體會發揮很大的作用.無癥狀感染者的出現頻率和傳染性是新冠病毒大流行的主要原因，在一項研究中，將流行病學數據與估計數據的44%的無癥狀感染者比例進行了比較，發現無癥狀感染的個體比輸入病例更容易引起更大的疫情［5］.為了更加深入地了解新冠病毒的快速傳播與無癥狀感染者之間的關系，一大批的專家學者建立了相關的傳染病模型.DOBROVOLNY［6］建立了一個包含無癥狀感染的倉室數學模型，預測到在感染高峰期會有更多的無癥狀或未報告的病例.該研究顯示，即使無癥狀感染不一定占感染的很大比例，它仍可以改變流行病的規模和致命性.但該模型有一點不足的是，尚未考慮疾病的潛伏期，這就可能導致同一個倉室內包含有不同感染率的人，這種個體的混合對參數估計的準確性會有很大影響.GU等［7］建立了一類包括住院、隔離和檢疫的SEIAQHR模型，通過詳細的數值模擬結果強調了社交距離、隔離和檢疫等干預措施的必要性.SUN等［8］基于一個來自黑龍江省的數據驅動模型SCIRA模型來估計無癥狀患者的影響，結果表明由于無癥狀患者也具有傳染性，這些隱蔽病例的潛在影響應引起廣泛關注.

收稿日期：2022-12-29;修回日期：2023-09-22.

基金項目：國家自然科學基金（11701528）.

作者簡介：原玉茹（1997-），女，山西晉城人，中北大學碩士研究生，研究方向為生物數學，E-mail：yuanyrjy@126.com.

通信作者：李淑萍，E-mail：lspnuc@126.com.

引用本文：原玉茹，李淑萍.具有無癥狀感染的新冠病毒傳播模型研究［J］.河南師范大學學報（自然科學版），2024，52（3）：71-79.（Yuan Yuru，Li Shuping.A study of a COVID-19 transmission model with asymptomatic infection［J］.Journal of Henan Normal University（Natural Science Edition），2024，52（3）：71-79.DOI：10.16366/j.cnki.1000-2367.2022.12.29.0001.）

上述各種研究表明，無癥狀感染者這些隱藏病例，對于傳染病建模而言無疑是不可忽略的.

在本文中，建立了一個包含無癥狀感染的病毒流行的倉室模型，并進行動力學分析，以確定無癥狀個體在新冠病毒傳播中發揮的作用.

1? 模型的建立

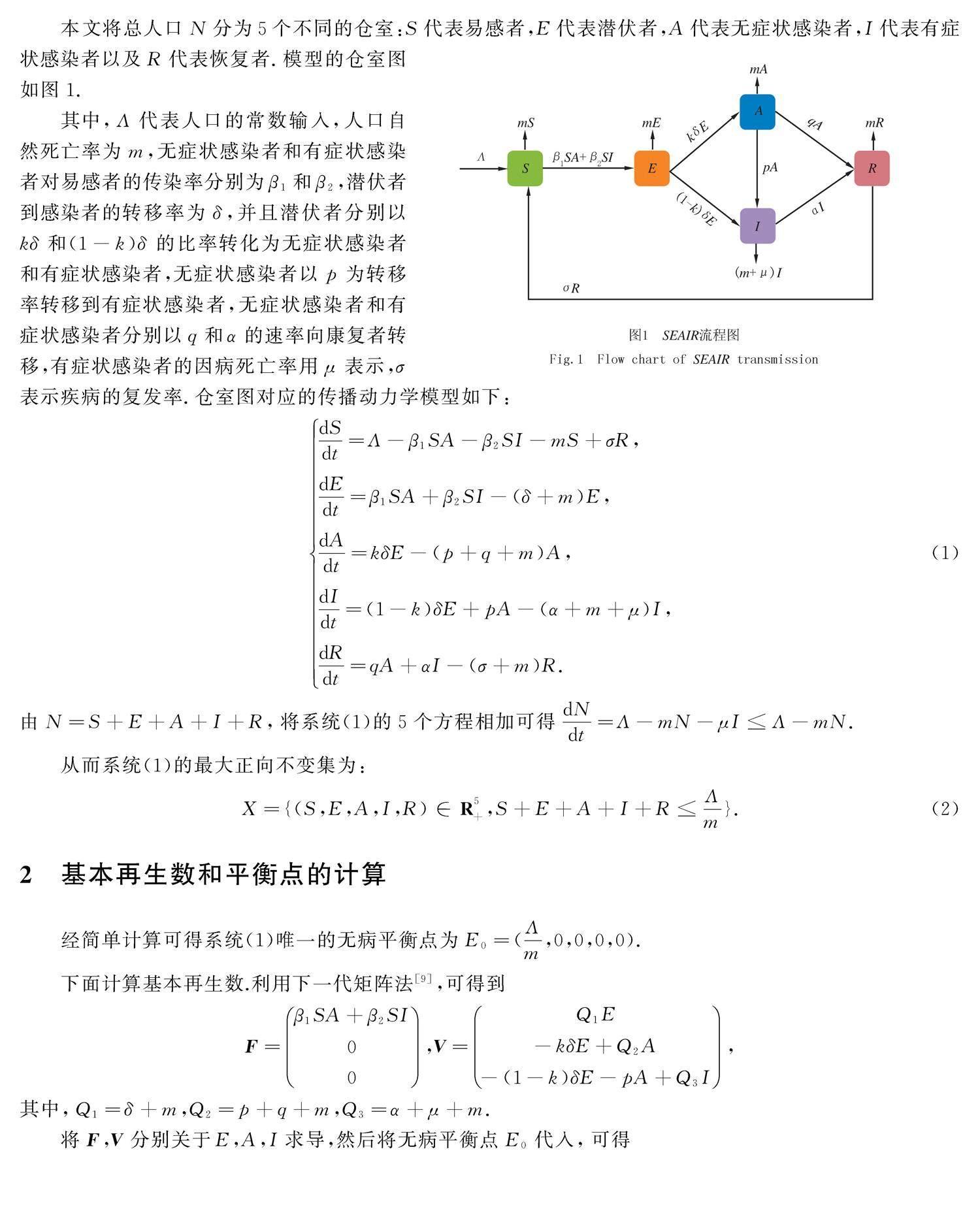
本文將總人口N分為5個不同的倉室：S代表易感者，E代表潛伏者，A代表無癥狀感染者，I代表有癥狀感染者以及R代表恢復者.模型的倉室圖如圖1.

其中，Λ代表人口的常數輸入，人口自然死亡率為m，無癥狀感染者和有癥狀感染者對易感者的傳染率分別為β1和β2，潛伏者到感染者的轉移率為δ，并且潛伏者分別以kδ和（1-k）δ的比率轉化為無癥狀感染者和有癥狀感染者，無癥狀感染者以p為轉移率轉移到有癥狀感染者，無癥狀感染者和有癥狀感染者分別以q和α的速率向康復者轉移，有癥狀感染者的因病死亡率用μ表示，σ表示疾病的復發率.倉室圖對應的傳播動力學模型如下：

dSdt=Λ-β1SA-β2SI-mS+σR，dEdt=β1SA+β2SI-（δ+m）E，dAdt=kδE-（p+q+m）A，dIdt=（1-k）δE+pA-（α+m+μ）I，dRdt=qA+αI-（σ+m）R.（1）

由N=S+E+A+I+R，將系統（1）的5個方程相加可得dNdt=Λ-mN-μIΛ-mN.

從而系統（1）的最大正向不變集為：X=｛（S，E，A，I，R）∈R5+，S+E+A+I+RΛm｝.（2）

2? 基本再生數和平衡點的計算

經簡單計算可得系統（1）唯一的無病平衡點為E0=（Λm，0，0，0，0）.

下面計算基本再生數.利用下一代矩陣法［9］，可得到

F=β1SA+β2SI00，V=Q1E-kδE+Q2A-（1-k）δE-pA+Q3I，

其中，Q1=δ+m，Q2=p+q+m，Q3=α+μ+m.

將F，V分別關于E，A，I求導，然后將無病平衡點E0代入，可得

F=0β1Λmβ2Λm000000，V=Q100-kδQ20-（1-k）δ-pQ3.

從而有FV-1=kδβ1ΛmQ1Q2+（1-k）δβ2ΛmQ1Q3+kδpβ2ΛmQ1Q2Q3β1ΛQ3+pβ2ΛmQ2Q3β2ΛmQ3000000.

因此，基本再生數為R0=r1+r2+r3，（3）

其中，r1=kδβ1ΛmQ1Q2，r2=（1-k）δβ2ΛmQ1Q3，r3=kδpβ2ΛmQ1Q2Q3.

將系統（1）的地方病平衡點記為E*=（S1，E1，A1，I1，R1）.為求解地方病平衡點，令模型（1）右端為0，即Λ-β1S1A1-β2S1I1-mS1+σR1=0，β1S1A1+β2S1I1-（δ+m）E1=0，kδE1-（p+q+m）A1=0，（1-k）δE1+pA1-（α+m+μ）I1=0，qA1+αI1-（σ+m）R1=0.（4）

可解得S1=Q1Q2Q3kδβ1Q3+（1-k）δβ2Q2+kδpβ2，E1=Q2kδA1，

A1=R0-1R0kδQ3（σ+μ）Q1Q2Q3（σ+μ）-σkδqQ3-σα（1-k）δQ2-σαkδp，

I1=（1-k）Q2+kpkQ3A1，R1=kqQ3+α（1-k）Q2+αkpk（σ+m）Q3A1.

經計算，S1，E1，A1，I1，R1均為正.因此，當R0＞1時，系統（1）存在唯一的地方病平衡點E*=（S1，E1，A1，I1，R1）.

3? 平衡點的穩定性

3.1? 無病平衡點的穩定性

定理1? 當R0＜1時，系統（1）的無病平衡點E0在X內是局部漸近穩定的；當R0＞1時，無病平衡點不穩定.

證明? 系統（1）在E0處的Jacobian矩陣為J|E0=-m0-β1Λm-β2Λmσ0-Q1-β1Λm-β2Λm00kδ-Q2000（1-k）δp-Q3000qα-（σ+m）.

矩陣J|E0的特征方程為（λ+m）（λ+σ+m）（λ3+b1λ2+b2λ+b3）=0.（5）

顯然，已有λ1=-m，λ2=-（σ+m）為方程（5）的兩個負實根，并且b1=Q1+Q2+Q3＞0，b2=Q1Q2（1-R1）+Q1Q3（1-R2）+Q2Q3＞0，b3=Q1Q2Q3（1-R0）＞0.

進一步得：b1b2-b3=Q1（Q1+Q2+Q3）（Q2（1-R1）+Q3（1-R2））+Q2Q3（Q2+Q3）+Q1Q2Q3R0＞0.

因此，由Hurwitz判據［10］可知，當R0＜1時，系統（1）在無病平衡點E0處局部漸近穩定.當R0＞1時，b3＜0，此時無病平衡點不穩定.

定理2? 當R0＜1時，系統（1）的無病平衡點E0在X內是全局漸近穩定的.

證明? 構造Lyapunov函數V=（kδQ1Q2β1+kδp+（1-k）δQ2Q1Q2Q3β2）E+（β1Q2+pβ2Q2Q3）A+β2Q3I＞0.

當R0＜1時，dVdt=（kδQ1Q2β1+kδp+（1-k）δQ2Q1Q2Q3β2）E′+（β1Q2+pβ2Q2Q3）A′+β2Q3I′=

（kδQ1Q2β1+kδp+（1-k）δQ2Q1Q2Q3β2）（β1SA+β2SI-（δ+m）E）+（β1Q2+

pβ2Q2Q3）（kδE-（p+q+m）A）+β2Q3（（1-k）δE+pA-（α+m+μ）I）=

（R0-1）（β1A+β2I）0.

令Ω=｛（S，E，A，I，R）|dVdt=0｝=｛（S，E，A，I，R）|A=I=0｝，在Ω內，當t→∞時，有S→Λm，因此｛E0｝是Ω的最大ω不變集.從而由LaSalle不變集原理可知，X內的任何軌線都趨于E0，無病平衡點E0在X內全局漸近穩定.

3.2? 地方病平衡點的穩定性

定理3? 當R0＞1時，若滿足c（ab-c）＞a2e及（ae-f）（abc-c2-a2e）＞f（ab-c）2+af2，那么系統（1）的地方病平衡點E*在X內是局部漸近穩定的.其中，a=a11+a12+m+a13，b=a14-a15+a11（a12+m+a13）+（a12+m）a13，

c=a11a13（a12+m）+（a14-a15）（a12+m+a13）+a12a15，

e=a13（a12+m）（a14-a15）+a12（a16+a13a15-σα（1-k）δ-σkδq），f=a12（a13a16-ασpkδ-ασ（1-k）δQ2-σqkδQ3）.

且有a11=Q1+Q2+Q3，a12=β1A1+β2I1，a13=σ+m，

a14=Q1Q2+Q1Q3+Q2Q3，a15=（1-k）δβ2S1+kδβ1S1，a16=Q1Q2Q3.

證明? 系統（1）在E*處的Jacobian矩陣為J|E*=-β1A1-β2I1-m0-β1S1-β2S1σβ1A1+β2I1-Q1β1S1β2S100kδ-Q2000（1-k）δp-Q3000qα-（σ+m）.

J|E*的特征方程為λ5+aλ4+bλ3+cλ2+eλ+f=0.（6）

經計算可得，a，b，c，e，f＞0.當R0＞1時，若滿足以下條件［11］：

（i）c（ab-c）＞a2e;（ii）（ae-f）（abc-c2-a2e）＞f（ab-c）2+af2.

那么矩陣J|E*的5個特征值均有負實部.通過Hurwitz判據可知，系統（1）的地方病平衡點E*在X內是局部漸近穩定的.

4? 系統的持續性

定理3? 當R0＞1時，系統（1）是一致持續的，即存在一個正數ε，使得limt→∞ inf（A（t），I（t），R（t））（ε，ε，ε）.

證明? 首先由集合X見式（2），定義集合X0=｛（S，E，A，I，R）∈X|E，A，I，R＞0｝，X0=X＼X0.

由系統（1）第2個方程可得：E（t）E（t0）e-（σ+m）（t-t0）＞0，（7）

由系統（1）第3個方程可得：A（t）A（t0）e-（p+q+m）（t-t0）＞0，（8）

由系統（1）第4個方程可得：I（t）I（t0）e-（α+μ+m）（t-t0）＞0，（9）

由系統（1）第5個方程可得：R（t）R（t0）e-（σ+m）（t-t0）＞0.（10）

因此X和X0是正不變集，X0是X的相對閉集.接下來證明系統（1）是一致持續的.記M=｛（S（0），E（0），A（0），I（0），R（0））|（S（t），E（t），A（t），I（t），R（t））∈X0，t0｝.

現在證明M=｛（S（0），0，0，0，0）|S（t）0｝顯然已有｛（S（0），0，0，0，0）|S（t）0｝M下面只需要證M｛（S（0），0，0，0，0）|S（t）0｝.

設（S（0），E（0），A（0），I（0），R（0））∈M則需證明對t0，有E（t）=0，A（t）=0，I（t）=0，R（t）= 0.利用反證法，假設結論不成立，則存在t00，使得下式之一成立：

（i）A（t0）＞0;（ii）I（t0）＞0;（iii）R（t0）＞0;（iv）E（t0）＞0.

對于情況（i），對式（8）形式求解可得對所有t＞t0，有A（t）＞0.進一步由系統（1）可得E（t）＞0，I（t）＞0，R（t）＞0.因而有（S（t），E（t），A（t），I（t），R（t））X0，產生矛盾.對于情況（ii）和情況（iii），由同樣的方法也可得出與（S（0），E（0），A（0），I（0），R（0））∈M矛盾.而對于第（iv）種情況，即E（t0）＞0，當t＞t0時，可得A（t）=A（t0）e-（p+q+m）（t-t0）+∫tt0kδEe（p+q+m）tdt，顯然E（t0）＞0時，對于t＞t0，有A（t）＞0.同理可求得I（t）和R（t）的形式解，當t＞t0時有I（t）＞0，R（t）＞0.因此（S（t），E（t），A（t），I（t），R（t））X0，得出矛盾.從而證得M=｛（S（0），0，0，0，0）|S（0）0｝.系統（1）的無病平衡點E0全局漸近穩定，在M中只有一個平衡點E0.

下面將證明E0相對于集合X0是弱排斥的，即證limt→∞? sup d（Φ（t），E0）＞0，僅需證明Ws（E0）∩X0=即可.利用反證法，假設此結論不成立，則系統（1）存在一個正解（S（t），E（t），A（t），I（t），R（t）），使得limt→∞（S（t），E（t），A（t），I（t），R（t））=（S0，0，0，0，0）.

定義M=F-V，因為R0＞1，所以s（M）＞0.對于足夠小的ε＞0，有s（M-Mε）＞0.其中，

Mε=0β1εβ2ε000000.

存在T＞0，使得對任意的t＞T，有S0-ε＜S（t）＜S0+ε.

從而可得如下微分方程不等式dEdtβ1（S0-ε）A+β2（S0-ε）I-（δ+m）E，

dAdt=kδE-（p+q+m）A，dIdt=（1-k）δE+pA-（α+m+μ）I.

考慮輔助系統dEdt=β1（S0-ε）A+β2（S0-ε）I-（δ+m）E，

dAdt=kδE-（p+q+m）A，dIdt=（1-k）δE+pA-（α+m+μ）I.（11）

因為s（M-Mε）＞0，所以當t→∞時，E（t）→∞，A（t）→∞，I（t）→∞，這與假設t→∞時，E（t）→0，A（t）→0，I（t）→0相矛盾［12］，從而證得Ws（E0）∩X0=.綜上所述，可得系統（1）關于（X0，X0）是一致持續的.

5? 最優控制理論

由于傳染病的建模一般都涉及大量的參數，因此研究具有最佳控制干預措施的疾病動態就顯得很有必要，為了使模型能夠比較精準地預測現實，最優控制理論常被用來提出最有效的策略以便減少人們的疾病負擔.以下針對新冠病毒的傳播，提出并研究了4種控制策略，目標是在疫情防控期間盡量減少受感染人數和相應策略的成本.

定義U=｛ui|i=1，2，3，4｝其中u1表示減少易感者與無癥狀感染者接觸的隔離策略，u2表示減少易感者與有癥狀感染者接觸的隔離策略，u3表示提高無癥狀感染者的治療恢復率的控制策略，u4表示提高有癥狀感染者的治療恢復率的控制策略.將與時間相關的控制納入系統（1）中，用以確定控制疾病的最優策略，可得到非線性微分方程組如下：dSdt=Λ-β1（1-u1）SA-β2（1-u2）SI-mS+σR，

dEdt=β1（1-u1）SA+β2（1-u2）SI-（δ+m）E，

dAdt=kδE-（p+q+m+u3）A，dIdt=（1-k）δE+pA-（α+m+μ+u4）I，dRdt=qA+αI+u3A+u4I-（σ+m）R.（12）

目標函數是J（u1，u2，u3，u4）=∫T0（P1A+P2I+ω12u21+ω22u22+ω32u23+ω42u24）dt，其中P1和P2分別表示無癥狀感染者和有癥狀感染者的權重系數;ω1，ω2，ω3，ω4分別代表各個控制策略對應的權重系數;ω12u21，ω22u22，ω32u23，ω42u24分別表示對應的控制策略所需的成本.

控制集U=｛（u1（t），u2（t），u3（t），u4（t））|0ui（t）1，i=1，2，3，4｝，且ui（t）在［0，1］上是勒貝格可測的.

定義Y=（S，E，A，I，R）則目標集χ可表示為χ=｛Y（·）∈W1，1（［0，T］;R5）|Y（·）滿足式（1）和（12）｝.

存在u*=（u*1，u*2，u*3，u*4），使得J=（u*1，u*2，u*3，u*4）=minu1，u2，u3，u4∈UJ（u1，u2，u3，u4）.（13）

根據Pontryagin Maximum原理［13］，對于最終時間T上固定的問題（13），若U（·）∈χ為最優解，則存在一個非平凡的絕對連續映射λ∶［0，T］→R5，且λ（t）=（λ1（t），λ2（t），λ3（t），λ4（t），λ5（t）），稱為伴隨變量，有

（1）控制系統滿足dSdt=Hλ1，dEdt=Hλ2，dAdt=Hλ3，dIdt=Hλ4，dRdt=Hλ5.

（2）伴隨系統滿足dλ1dt=-HS，dλ2dt=-HE，dλ3dt=-HA，dλ4dt=-HI，dλ5dt=-HR.

（3）極小值條件H（Y*（t），U*（t），λ*（t））=min0＜ui＜uimaxH（Y*（t），U（t），λ*（t））.

對于t∈［0，T］成立，將哈密頓函數H定義為H（Y，U，λ）=P1A+P2I+ω12u21+ω22u22+ω32u23ω42u24+λ1［Λ-β1（1-u1）SA-

β2（1-u2）SI-mS+σR］+λ2［β1（1-u1）SA+β2（1-u2）SI-（δ+m）E］+

λ3［kδE-（p+q+m+u3）A］+λ4［（1-k）δE+pA-（α+m+

μ+u4）I］+λ5［qA+αI+u3A+u4I-（σ+m）R］，（14）

此外，有橫截條件λi（T）=0，i=1，2，…，5成立.

定理4? 存在最優控制U（t）以及最優解（S*（t），E*（t），A*（t），I*（t），R*（t））滿足最終時間T固定的最優控制問題（13），且存在伴隨函數λ*i（·），（i=1，2，…，5），使得dλ*1dt=［β1（1-u1）A+β2（1-u2）I］（λ*1-λ*2）+mλ*1，

dλ*2dt=（δ+m）λ*2-kδλ*3-（1-k）δλ*4，

dλ*3dt=-P1+β1（1-u1）S（λ*1-λ*2）+（p+q+m+u3）λ*3-pλ*4-（q+u3）λ*5，

dλ*4dt=-P2+β2（1-u2）S（λ*1-λ*2）+（α+m+μ+u4）λ*4-（α+u4）λ*5，

dλ*5dt=-σλ*1+（σ+m）λ*5，

且有橫截條件λ*i（T）=0，i=1，2，…，5.

更進一步得到最優控制解被表示為如下形式：u*1（t）=min｛max｛0，（λ*2-λ*1）β1S*A*ω1｝，1｝，u*2（t）=min｛max｛0，（λ*2-λ*1）β2S*I*ω2｝，1｝，

u*3（t）=min｛max｛0，（λ*3-λ*5）A*ω3｝，1｝，u*4（t）=min｛max｛0，（λ*4-λ*5）I*ω4｝，1｝.

6? 數值模擬

6.1? 平衡點的穩定性

假設Λ=100，β1=0.000 1，β2=0.000 1，m=0.07，δ=0.4，σ=0.03，k=0.6，p=0.3，q=0.6，α=0.3，μ=0.05，可得R0=0.31＜1，如圖2（a）所示，驗證了無病平衡點是全局漸近穩定的.假設β1=0.001，β2=0.001 4，δ=0.7，σ=0.05，q=0.485，μ=0.066，可得R0=3.87＞1，如圖2（b）所示，地方病平衡點是全局漸近穩定的.

6.2? 敏感性分析

敏感性分析用于描述輸入參數對輸出變量的影響程度，其主要方法之一的偏秩相關系數法（PRCC）是一種非常有用的統計抽樣技術，現已廣泛應用于分析傳染病模型領域［14］.本文通過利用拉丁超立方抽樣法，對影響系統（1）的基本再生數R0的各個參數進行了敏感性分析，進而對這些參數影響R0的程度有了一定的判斷.通過分析發現，在選取的參數中，m與R0呈顯著負相關，Λ，β1，β2，k與R0呈顯著正相關.從圖3中可以發現，在這些對疾病的暴發有著不同程度影響的參數中，無癥狀感染者對易感者的傳染率β1對R0的影響極大，因此可以通過降低β1來達到減少和控制傳染病傳播的目的；也可以通過增大無癥狀和有癥狀感染者的恢復率系數q和α來縮短傳染病的治愈周期；或者通過減小人口的常數輸入Λ來降低人口流動性，進而降低疾病的傳播速度.

6.3? 最優控制

在圖4（b，c）中，得到了采取最優控制策略前后無癥狀感染者和有癥狀感染者的數量對比，很明顯由于采取了控制策略，感染人數迅速趨近于0.這說明所研究的控制策略對于控制傳染病的傳播能夠起到很好的作用，證明了控制策略的有效性.

7? 結? 論

本文建立了具有無癥狀感染的SEAIR模型，針對無癥狀感染者在新冠肺炎傳播中的影響進行了研究.首先計算了模型的基本再生數，其次利用理論方法證明了無病平衡點的穩定性，并證明了系統的一致持續性.然后應用龐特里亞金極大值原理對一個最優控制問題進行了求解.最后通過數值模擬驗證了理論結果的可靠性，并對參數進行敏感性分析，說明無癥狀感染者對疾病的傳播影響不容忽視.隔離和社交距離是阻止感染傳播的主要武器，因此國家可以重點從這方面入手，通過采取適當的措施，實行完善的隔離政策，提升人們對病毒的防范意識，減少易感人群與染病者之間的接觸，最終達到控制疾病傳播的目的.

參? 考? 文? 獻

［1］ ??KARIA R，GUPTA I，KHANDAIT H，et al.COVID-19 and its modes of transmission［J］.SN Comprehensive Clinical Medicine，2020，2（10）：1798-1801.

［2］LI X P，WANG Y，KHAN M A，et al.A dynamical study of SARS-COV-2：a study of third wave［J］.Results in Physics，2021，29：104705.

［3］KUMARI P，SINGH H P，SINGH S.SEIAQRDT model for the spread of novel coronavirus（COVID-19）：a case study in India［J］.Applied Intelligence，2021，51（5）：2818-2837.

［4］KANG X X，HU Y，LIU Z Y，et al.Forecast and evaluation of asymptomatic COVID-19 patients spreading in China［J］.Results in Physics，2022，34：105195.

［5］SUN T Z，WENG D.Estimating the effects of asymptomatic and imported patients on COVID-19 epidemic using mathematical modeling［J］.Journal of Medical Virology，2020，92（10）：1995-2003.

［6］DOBROVOLNY H M.Modeling the role of asymptomatics in infection spread with application to SARS-CoV-2［J］.PLoS One，2020，15（8）：e0236976.

［7］GU Y，ULLAH S，KHAN M A，et al.Mathematical modeling and stability analysis of the COVID-19 with quarantine and isolation［J］.Results in Physics，2022，34：105284.

［8］SUN T Z，WANG Y.Modeling COVID-19 epidemic in Heilongjiang Province，China［J］.Chaos，Solitons & Fractals，2020，138：109949.

［9］VAN DEN DRIESSCHE P，WATMOUGH J.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission［J］.Mathematical Biosciences，2002，180（1/2）：29-48.

［10］馬知恩，周義倉，王穩地，等.傳染病動力學的數學建模與研究［M］.北京：科學出版社，2004.

［11］LASALLE J P.動力系統的穩定性［M］.成都：四川科學技術出版社，2002.

［12］ZHANG F，ZHAO X Q.A periodic epidemic model in a patchy environment［J］.Journal of Mathematical Analysis and Applications，2007，325（1）：496-516.

［13］LI K Z，ZHU G H，MA Z J，et al.Dynamic stability of an SIQS epidemic network and its optimal control［J］.Communications in Nonlinear Science and Numerical Simulation，2019，66：84-95.

［14］李淑萍，苗慧.數據驅動下帶環境病毒的新冠肺炎傳播模型［J］.山西大學學報（自然科學版），2023，46（1）：131-140.

A study of a COVID-19 transmission model with asymptomatic infection

Yuan Yuru， Li Shuping

（School of Mathematics， North University of China， Taiyuan 030051， China）

Abstract： In order to study the influence of asymptomatic infection on the transmission of novel coronavirus， a transmission dynamics model of COVID-19 with asymptomatic infection is established. First， the basic reproduction number is obtained by the next generation matrix method. Secondly， when R0＜1， Hurwitz criterion is applied to prove the local stability of the disease-free equilibrium， and the global stability of the disease-free equilibrium is proved by constructing a lyapunov function; and when R0＞1， there is a unique endemic equilibrium and the system is locally asymptotically stable， proving the uniform persistence of the system. Then， using the optimal control theory， the expression form of the optimal control solution is solved. Finally， the theoretical results are verified by numerical simulation， and the sensitivity analysis of the parameters showed that the influence of asymptomatic infection on the transmission of novel coronavirus can not be ignored， and compulsory isolation measures should be taken to reduce the transmission rate of the disease.

Keywords： asymptomatic infection; stability; uniformly persistent; optimal control; sensitivity analysis

［責任編校? 陳留院? 趙曉華］