淺談萬有引力定律常見考查題型特點及解題思路

劉文彬

【摘要】萬有引力定律是物理學中的一個基本定律，它描述了兩個物體之間的引力關系.在教學和考試中，對萬有引力定律的理解和應用是非常重要的.本文旨在對萬有引力定律的常見考查題型進行探討，并提供解題思路.重點分析三種主要的題型：軌道比較問題、雙星問題和衛星變軌問題.對于每一種題型，都將提供具體的解題策略，并通過實例進行說明，幫助學生更有效地理解和解決這些題型.

【關鍵詞】萬有引力定律；高中物理；解題技巧

只要物體具有質量，就一定存在萬有引力，因此萬有引力無處不在.高中物理中，萬有引力定律的考查十分常見，通常以選擇題形式出現，絕大多數情況都是以天體運動問題進行設問.本文結合具體例題分別介紹三類常見的考查題型和解題思路，幫助學生理解萬有引力，運用萬有引力定律求解相關問題.

1 軌道比較問題

衛星處于不同軌道有著不同作用，如近地衛星和同步衛星的運行軌道就有一定區別.比較不同類型衛星的相關參數屬于比較常見的萬有引力應用問題，解題時首先要明確衛星向心力與萬有引力的關系，其次列出相關等式，得到所求物理量與軌道半徑之間的關系，從而對問題進行解答.

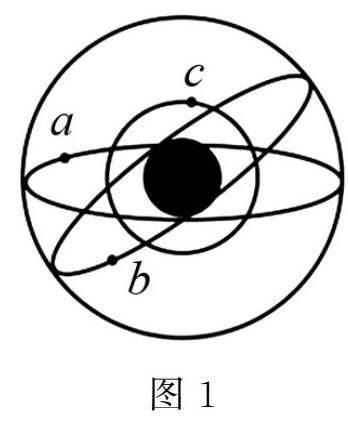
例1 2020年8月1日，在北京人民大會堂上，對我國的北斗3號全球衛星導航系統建成舉辦了開通儀式，宣布了我國北斗3號全球衛星正式進行使用.而北斗3號全球衛星在宇宙中的運行軌道如圖1所示，已知a，b，c衛星均圍繞著地球做圓周運動，a是地球的同步衛星，a、b的運行軌道半徑相同.下列說法正確的是（ ?）

（A）圖中的a衛星的角速度要比c衛星的角速度小.

（B）圖中的a衛星的角速度要比b衛星的角速度大.

（C）圖中的a衛星的角速度要比第一宇宙的速度大.

（D）圖中的b衛星的運動的周期等于24h.

思考 不同軌道的衛星角度比較，首先需要列出相關等式分析角速度、加速度與軌道半徑的關系，其次根據萬有引力定律求解周期和運行速度，即可對問題作出解答.

解析 由牛頓第二定律可得GMmr2=mv2r.衛星的線速度公式為v=GMr，則衛星的角速度公式為ω=vr=GMr3，可知軌道半徑大的衛星角速度小，所以衛星a的角速度小于c的角速度，故選項（A）正確；

衛星的加速度為a=v2r=GMr2.根據題目能夠了解到，軌道半徑大的衛星，相對應的加速度是比較小的，所以在圖中的衛星a與b的加速度大小兩者是相等的，所以能夠排除（B）選項；

第一宇宙速度相比較衛星圍繞地球圓周運動時的速度會更大，它是最大的環繞速度，所以途中的a衛星會比第一宇宙速度會更小，排除（C）選項；

衛星a與b的軌道半徑相同，角速度相等，則周期也相等，所以衛星b的周期等于24h，故選項（D）正確；

綜上，正確答案為（A）（D）.

2 雙星問題

雙星問題是萬有引力在高中物理中應用的一個重要內容，一般是考查雙星的向心力來源、周期之比、線速度等物理量之比，具有一定難度.求解雙星問題的關鍵，需要理解向心力是有相互作用的萬有引力提供，并且根據萬有引力公式能得到周期、總質量的表達式，也能知道兩個星球到中心的距離半徑與質量成反比，利用這些特點，能對問題作出具體解答.

例2 2023年6月，中國天眼FAST發現了一個名為PSRJ1953+1844的雙星系統.假設該雙星系統是由兩顆質量之和為M的脈沖星組成，兩者之間距離為L，繞連線上某點做勻速圓周運動，引力常量為G，求該雙星系統的運行周期T.

思考 首先根據萬有引力定律和牛頓運動定律公式，列出相對應等式，其次根據質量、距離之和的具體值列式，聯立這些等式，運算找到運行周期T的表達式即可.

解析 設雙星系統中兩個星球質量分別為m1，m2，其圓周運動半徑分別為r1，r2，根據萬有引力定律和牛頓第二定律，對星球m1有Gm1m2L2=m1·4π2T2r1，對星球m2有Gm1m2L2=m2·4π2T2r2，又m1+m2=M，r1+r2=L，聯立可得T=2πL3GM.

3 衛星變軌問題

衛星變軌問題是常見的一類萬有引力問題，如果一個做勻速圓周運動的衛星的速度受到一些因素的影響而產生了變化，那么此時萬有引力就會進行改變，不再是原來的運行需要的向心力時，軌道就會出現改變.這類問題的求解首先要理解宇宙速度與衛星軌道的關系，其次利用萬有引力定律列式分析軌道半徑與角速度、加速度、環繞速度和周期的關系，就能得到問題答案.

例3 如圖2所示，在進行同步衛星發射的過程當中，如圖2所示衛星會首先進入到橢圓的軌道I，衛星運行到Q點時，增大衛星的速度，使其進入II軌道運行.則（ ?）

（A）這個衛星在地球進行發射時的發射速度一定大于11.2km/s.

（B）衛星在同步軌道II上的運行速度小于7.9km/s.

（C）衛星處于軌道II時加速度大于軌道I上通過Q點的加速度

（D）衛星在Q點通過加速實現由軌道I進入軌道II.

思考 首先理解第一宇宙速度，衛星將繞地球做圓周運動，當速度達到第二宇宙速度，衛星將離開地球圍繞太陽運動，其次根據萬有引力公式分析同一位置的加速度是否相等，并分析變軌需要的條件，最終得到正確答案.

解析 第二宇宙速度為11.2km/s，這個速度也是衛星脫離地球引力之后，所能夠產生的最小發射速度，但是，由于衛星在脫離地球引力之后，仍然需要圍繞著地球做圓周運動，故發射速度不能大于11.2km/s，選項（A）錯誤；

第一宇宙速度為7.9km/s，是衛星在地球表面飛行的速度，也是最小的發射速度，根據萬有引力提供向心力，可得GMmr2=mv2r，解得v=GMr.衛星在同步軌道II運行時，軌道半徑變大，運行速度小于7.9km/s，選項（B）正確；

只有在萬有引力作用情況下，有GMmr2=ma，解得a=GMr2.同一位置的加速度相等，衛星在軌道II上通過Q點加速度等于在軌道I上通過Q點的加速度，選項（C）錯誤；

衛星在Q點通過加速，做離心運動，由軌道I進入軌道II，選項（D）正確；

綜上，正確答案為（B）（D）.

4 結語

三類問題都是萬有引力定律常見的考查題型，且都具有一定難度.在同步衛星、近地衛星軌道參數的比較問題中，需要緊密結合萬有引力定律求解；在雙星問題中，需要聯合萬有引力和其他等式求解；在衛星變軌問題中，需要結合萬有引力定律理解不同軌道需要的速度與加速度.熟悉和掌握例題題型，能讓學生更有條理地分析問題，更巧妙地運用萬有引力定律解答不同問題.

參考文獻：

[1]羅煉.芻議高中物理中天體運動類題型的解題技巧[J].數理化解題研究（高中版），2016（11）：65.

[2]趙秋麗.關于萬有引力定律問題的兩種解題思路[J].中學生數理化（學研版），2020（09）：39-40.

[3]林梓博.對高中物理萬有引力定律的解題分析[J].新教育時代電子雜志（學生版），2017（15）：156.