例談微元法在高中物理解題教學中的巧用

陳峰

【摘要】微元法是一種解決物理問題的常用方法，將其應用于高中物理解題教學中，能夠幫助學生快速找到解題的正確思路，抓住問題的本質(zhì)，以此提高學生的解題效率和正確率.本文以實踐教學為例，討論微元法在物理解題教學中的應用，旨在創(chuàng)新物理習題教學形式，促進學生學科素養(yǎng)的綜合發(fā)展.

【關(guān)鍵詞】微元法；高中物理；解題教學

素質(zhì)教育背景下，高中物理的解題教學要突出對學生解決問題的能力、建模能力與邏輯思維等方面的培養(yǎng).在此背景下，傳統(tǒng)的題海戰(zhàn)術(shù)已不適用于素養(yǎng)指向下的物理學科教學，所以，教師必須改變教學形式，將微元法帶入高中物理解題教學中，幫助學生掌握物理學習、解題的技巧，引導學生攻克在物理學習時遇到的難關(guān).

1 微元法概述

微元法是一種常用于解決物理問題的方法，是一種將問題拆解成微小的微元，再由微元入手，分析問題主體，隨后解決整個問題的方法.所以，微元法的核心是微元，即通過巧妙的思路解析，將大問題化為小問題，將復雜問題化為簡單問題.在整個問題情境中，快速抓住可代表問題主體的極小部分，隨后再從微元，由點及面地分析整體并解決問題.使用微元法解決物理問題時，學生可以快速定位問題的核心，并找到解決問題的思路，適用于高中復雜的物理題型.在解答物理問題時，學生也能更深層次地理解物理規(guī)律的應用方式.

2 微元法的應用流程

2.1 取元

在使用微元法解題的過程中，取元是最重要的一步.學生必須在復雜的物理問題中快速找到元，選取最優(yōu)的元，才能找到該物理題目中的重點與核心問題.很多學生在使用微元法解題時，沒有找到問題的本質(zhì)，選擇的元是錯誤的，后續(xù)的解題思路與解題求和過程自然也會存在問題.取元必須遵循以下三點：第一，確保選取的元的計算是簡單的，這也是微元法的根本，即將復雜的問題簡單化，若元的計算過于復雜，也算是違背了使用微元法解題的初衷，沒能從根本上降低解題難度.第二，根據(jù)問題取得的元可以通過加權(quán)疊加得到結(jié)果，即在單個元的計算時，既要考慮到元自身的權(quán)重，又要考慮到元疊加后的整體意義，保證加權(quán)疊加后的元可以代表問題整體.這樣可以避免遺漏疊加或重復疊加.第三，取元的過程必須遵循物理規(guī)律，能體現(xiàn)出物理規(guī)律，加權(quán)疊加取得的微元，可以通過極限概念來解釋，若需要解答的習題是無限小的物理習題，那么便可以直接套用物理規(guī)律中的極限概念，可以不做限制地取元.

例1 已知有一個均勻的帶電圓環(huán)，半徑為r、帶電荷量為Q，帶電圓環(huán)的軸線處，有一P點，距離圓心長度為L，求P點電場強度.

靜電場中的問題情境種類較多，其中圓環(huán)、球面或圓餅等帶電物體較為特殊，學生在遇到這類題型時，很容易摸不著頭腦，不知如何下手.實際上，這類特殊帶電體的靜電場問題，主要是考查學生是否能完全理解靜電場這部分知識，是否了解了其中的抽象概念，能否靈活應用并遷移這部分內(nèi)容.此時，用微元法將各種特殊帶電物體分割成微小的元，再針對單一元開展計算，便可以快速得到問題答案.初次接觸這道題時，先立足整體讀題，隨后取元.在本題中，均勻的帶電圓環(huán)作為一個整體，可以分解成無數(shù)個微元.每一個微元都是整體的重要組成部分.因此，所有的元共同構(gòu)成了這個帶電圓環(huán).從題目中的已知條件可以得知，圓環(huán)各個部分的帶電量是均勻的，所以每一段微元都帶有相等的電荷量，符合取元規(guī)律，再根據(jù)庫侖定律便可以得出微元的電場強度.

2.2 模型化解元

選取正確的元以后，再將元轉(zhuǎn)化為求解過程，利用物理建模開展模型化解元.通過極限相等模型或?qū)颇Ｐ偷霓D(zhuǎn)換，能有效降低習題難度.轉(zhuǎn)化的過程便是物理建模的過程.之后，再通過針對元的簡單的計算，便可以快速找到解題思路.模型化解元的過程是微元法的核心，也是將復雜問題簡單化、抽象概念直觀化的方法.模型化解元也可以看作是將變量的元化為常量，并針對常量開展求解的過程.所以，正確使用模型化解元可以幫助學生快速簡化復雜的解題步驟，還可有效提高學生的做題速度.

例2 已知一圓環(huán)放置于水平面上，圓環(huán)內(nèi)有一顆光滑的小球，給小球施加力F后，小球繞圓環(huán)做半徑為R的圓周運動，已知力F的大小是恒定的，力F的作用方向沿圓環(huán)切線方向，求力F的做功大小.

在解答這一道題時，有很多同學看到題目后，便想利用W=FLcosα求解，但這個公式只能解決恒力做功.在本題中，力F的情況明顯為變力做功，因此不適用該公式，所以使用微元法解答變力做功問題，通過模型化解元，將變力F的做功轉(zhuǎn)化為恒力F的做功，便可以快速得出問題答案.不難看出，模型化解元的過程需要學生靈活運用此前學過的各項物理公式、物理定義，熟練掌握不同公式的應用特征、特殊應用場景，并在解題的過程中，正確使用各種物理公式進行解元，才能夠真正將復雜題目轉(zhuǎn)化成簡單題目，省略部分無用的解題步驟，快速得到問題答案.

2.3 用元求和

用元求和即在針對元開展簡單計算后，通過疊加求和得出最終結(jié)果的方式.對元的疊加求和，需要學生利用此前學習的物理知識以及部分數(shù)學知識，通過求和公式將數(shù)據(jù)疊加計算.可以說，用元求和是微元法在高中物理解題中降低題目難度的核心體現(xiàn)，通過疊加求和的方式，將復雜的問題化為最基礎(chǔ)的元，再通過簡單的計算形式解決復雜問題，能有效降低解答題目時的計算難度，還能提高學生解題的正確率.

例3 河上有一只靜止的船，船的質(zhì)量為M，長度為L，在不計算水阻力的前提下，有一名小朋友（質(zhì)量為m）在靜止的船上從船頭走到船尾.在小朋友運動過程中，船是否會發(fā)生位移，位移是多少？

這道例題相對復雜.先分析題目中的情境，即小朋友在船上走，船靜止于河上，將船的速率設(shè)置為v1，小朋友的速率設(shè)置為v2，題干中說到不計算水阻力，所以整個系統(tǒng)受到的合外力是零.根據(jù)動量守恒定律可以得出mv2=Mv1，此時取元，將小朋友在船上行走的時間總和切分成無數(shù)個微元的時間對象，以Δt表示，在Δt內(nèi)，小朋友從船頭走到船尾的任意一個時間段的運動狀態(tài)都可視作勻速運動，這是將整體時間切分為無限小的時間后微元的展現(xiàn)形態(tài)，所以，在Δt中，小朋友的位移Δs2=v2Δt.船的位移Δs1=v1Δt.繼續(xù)推導可得出mΔs2=MΔs1.將切分后的所有元單位疊加并求和后，m∑Δs2=M∑Δs1，題目中所述，小朋友從船頭走到船尾，所以小朋友相對于船的位移為船的總長度L，根據(jù)物理規(guī)律，L=s1+s2，由此便可計算出船的位移大小.

3 微元法在高中物理解題教學中的實踐應用案例

3.1 在“運動學”問題中使用微元法

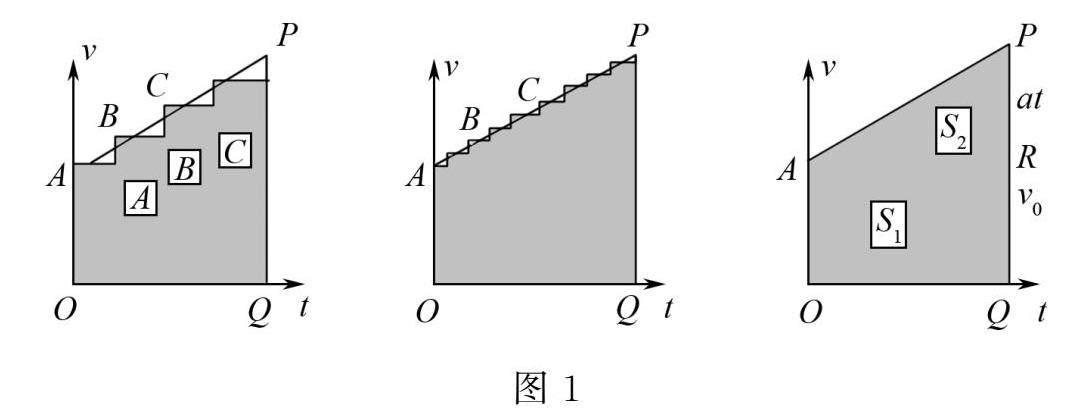
例4 某正做勻加速直線運動的物體，初始速度為v0，加速度為a，已知運動時間為t，位移為x，推導可用于表達x與t的關(guān)系式：x=v0t+at2.

使用微元法解題時，要先將該物體加速直線運動的整個運動過程分解成無數(shù)個細小的微元，隨后將微元置于平面直角坐標系中，開展模型化解元.在直角坐標系中，微元可以看作是以高為t，以縱軸長度為上下底的梯形.t越小，坐標系中的梯形就越趨近于長方形.如圖1所示，將圖中的陰影面積看作是物體的總位移，便在平面直角坐標系中構(gòu)建出了位移和時間的模型，想要求陰影部分的面積，可以將下半部分的長方形與上半部分的三角形面積相加，即x=v0t+at2，至此，完成了表達x與t關(guān)系式的推導.在解題時，通過微元法直觀地展示出了速度和時間的變化關(guān)系，模型化解元的過程精簡凝練，模型相對理想，使用數(shù)形結(jié)合思想解釋位移的幾何函數(shù)后，便可以完成關(guān)系式的推導與論證.

3.2 在“靜力學”問題中使用微元法

例5 將一個均勻的質(zhì)量為m的圓形繩套在一個光滑的圓錐體上.圓錐體的頂角為α，光滑圓錐體置于水平面上.求圓形繩平衡時繩的張力大小.

細繩類問題區(qū)別于常規(guī)的受力分析題，這類問題的情境特殊，如果使用常規(guī)的思路分析解題，那么學生很容易陷入思維誤區(qū)，解題難度較大.使用微元法，便可以快速定位問題關(guān)鍵，完成受力分析.題目中可得到的已知條件相對較少，僅有圓形細繩的質(zhì)量和圓錐體頂角這兩個直接條件.先通過取元，將圓形細繩分化為均等的若干個微元，微元質(zhì)量為Δm，微元對應的圓心角設(shè)置為Δθ，單獨對微元做受力分析，該微元受到周邊細繩的兩個測拉力、微元自身重力以及圓錐體面給的支撐力，且微元處于受力平衡狀態(tài).此時再進行運算，便可以得出微元所受的張力大小，再通過疊加求和，即可得出圓形細繩平衡狀態(tài)下受到的張力大小.總結(jié)來說，在解決細繩類受力分析題型時，使用微元法轉(zhuǎn)換視角，將整體變?yōu)闃O微小的元后，找到微元質(zhì)量和細繩整體間的質(zhì)量關(guān)系，在受力分析后便能得出問題答案.

3.3 在“電磁感應”問題中使用微元法

例6 有一足夠長的條形勻強磁場，處于一定空間內(nèi)，以等距離狀態(tài)分布.該勻強磁場的磁感應強度大小B=1T，磁感由方向垂直紙面向里，相鄰磁場寬度d=0.5m，假設(shè)現(xiàn)有一質(zhì)量為m=0.1kg，邊長為L=0.2m，電阻為R=0.1Ω的正方形線框位于勻強磁場左側(cè)，自磁場邊緣水平進入磁場，正方形線框的速度為v0=7m/s，求該線框可以完整地穿過條形磁場區(qū)域的個數(shù)n.

高中物理電磁感應這部分題目，主要考查學生是否了解了電磁感應的本質(zhì)，能否把握其中的物理規(guī)律，這類題目復雜多變，問題情境復雜，思路多變且極其靈活，在學生使用常規(guī)思路找不到突破點的時候，便可以使用微元法，根據(jù)問題中的情境正確取元，隨后再通過建元建模和疊加求和得出問題答案.根據(jù)題目中的線索，線框運動過程中僅在進入磁場、離開磁場時才會相應地生成感應電動勢.在垂直紙面向里的勻強磁場中，線框水平切割速度為v時，F(xiàn)安=B2L2vR，將整個運動過程切分成極其微小的元，取其中道極短時間設(shè)置為Δt，再根據(jù)動量定理，便可以得到F安·Δt=m·Δv，之后再求解，便可得出問題答案.

4 結(jié)語

微元法是高中物理解題教學中的常用方法，能夠?qū)碗s的物理題目簡單化.通過取元、解元、用元，可以快速找到問題核心，將復雜的概念拆分成基礎(chǔ)的元結(jié)構(gòu)，再利用模型化解元將抽象內(nèi)容轉(zhuǎn)化為具象內(nèi)容，將變量變化為常量；之后，使用各種物理規(guī)律、物理定律，對基礎(chǔ)的元結(jié)構(gòu)進行分析與處理，構(gòu)建物理模型；最后，再通過元的加權(quán)疊加求和等方法，便可以直接得到題目答案.掌握微元法不僅能有效提高學生的解題能力、解題速度以及解題準確性，還可以培養(yǎng)學生的物理建模思維、邏輯推理能力，可以幫助學生鞏固基礎(chǔ)、牢固根基，能從根本上提高學生的物理水平.

參考文獻：

[1]劉洋.解題有法游刃有余——微元法在高中物理解題中的妙用[J].理科愛好者，2022（06）：33-35.

[2]張旎.微元法在高中物理解題中的應用[J].數(shù)理化解題研究，2022（36）：80-82.

[3]謝發(fā)明.善用微元法，巧妙解難題[J].第二課堂（D），2022（10）：7.

[4]臧凱泉.微元法在高中物理解題中的有效應用研究[J].數(shù)理化解題研究，2022（21）：70-72.

[5]謝海華.高中物理解題中微元法的應用[J].高中數(shù)理化，2021（S1）：91-92.