例析牛頓運動定律在不同模型中的應用
趙興華


【摘要】牛頓運動定律是解答高中物理運動問題的一個重要知識點,可以應用在多種模型中,常見的模型有斜面模型、板塊模型、連接體模型等.熟悉牛頓運動定律在不同常見模型中的應用,是學生必須掌握的重要學習內容.本文從三個模型切入,結合具體例題分析如何在模型中應用牛頓運動定律,幫助學生解題.
【關鍵詞】牛頓運動定律;高中物理;解題技巧
牛頓運動定律,作為物理學的基石,已在各種實際問題和模型中得到了廣泛應用.這些應用既體現出牛頓運動定律的普適性,也揭示了其在解決復雜現象時的巨大潛力.通過建構模型的方式將這一理論與實際問題相結合,以形象、具體的方式展現其效用,是促進理論和實踐對接的重要途徑.
1 連接體模型
連接體模型是借助介質或直接接觸使兩個或多個物體連接在一起并運動的模型,一般會用牛頓第二定律解答這類問題.隔離思路或臨界思路都是解答連接體模型的常見思路,首先判斷整體的運動狀態,其次分析單個物體的運用狀態,根據牛頓運動定律列出等式并解答,可得到最終答案.
例1 如圖1所示,豎直放置在水平面上的輕彈簧上放著質量為8kg的物體A,處于靜止狀態,將一個質量為2kg物體B放在A上的一瞬間(g取10m/s2),B對A的壓力大小為( ?)
(A)18N. ??(B)16N.
(C)10N. (D)6N.
思考 首先將物體A、B看做一個整體,運用牛頓第二定律分析整個物體的加速度,其次對物體隔離分析,憑借牛頓運動定律列出等式,即可得到壓力的大小.
解析 由題意可知,原來彈簧的彈力大小等于A的重力大小,即F=mAg,放上B的瞬間,彈簧的彈力不變,對A、B組成的整體分析,根據牛頓第二定律得a=mA+mBg-FmA+mB=mBgmA+mB=2m/s2.
對B隔離分析,有mBg-N=mBa,N=mBg-a=16N.
由牛頓第三定律可知,B對A的壓力為16N.
2 傳送帶模型
傳送帶模型屬于動力學中較為經典的一類問題,也是牛頓運動定律的應用題型.求解傳送帶模型問題,主要是尋找共速點,即傳送帶上物體與傳送帶以相同速度v運動的點.解題時,首先運用牛頓運動定律求解共同速度,其次以共速點作為轉折點分析運動狀態和具體位移,即可得到最終答案.
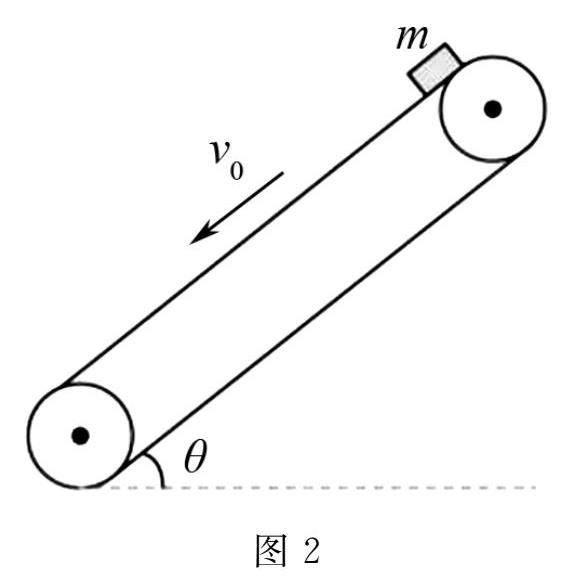
例2 圖2為煤塊傳送裝置的簡化圖,已知傾斜傳送帶逆時針運轉速率為v0=10m/s,傾角為θ=37°,某時刻將煤塊輕放在傳送帶頂端,已知兩電機輪間的距離為L=1.8m,煤塊和傳送帶之間的動摩擦因數為μ=0.5,不計傳送帶電機輪的尺寸大小.取重力加速度大小g=10m/s2,則煤塊滑離傳送帶下端時傳送帶上的劃痕長度為.
思考 首先煤塊在傳送帶上做勻加速運動,根據牛頓第二定律求出到達共同速度時需要的時間和位移,其次分析煤塊與傳送帶之間的相對位移,才能得到最終答案.
解析 當煤塊剛放到傳送帶上達到傳送帶速度前,對煤塊進行受力分析,根據牛頓第二定律可知mgsin37°+μmgcos37°=ma.解得a=10m/s2,到達共速需要的時間為t1=v0a=1s,煤塊以這個加速度一直勻加速下滑到底端時,L=12at2,解得t=0.6s<t1.此時煤塊不與傳送帶共速,此過程中傳送帶走過的距離為x=v0t=6m.此過程中煤塊相對傳送帶的路程為Δx=x-L=4.2m>2L=3.6m.可知煤塊在傳送帶上劃痕長度為3.6m.
3 等時圓模型
等時圓模型具體指物體從同一豎直圓所有經過圓周最低點的光滑弦上靜止下滑,所通過的時間都相等的模型.靈活運用等時圓和牛頓運動定律,可以達到簡化問題的目的,首先根據牛頓運動定律找到下滑時間t與圓半徑r之間的關系等式,其次以軌道為直徑作圓,分析半徑比,即可得所用時間比,從而達到解決問題的目的.
例3 如圖3所示,處于豎直平面內的某圓周的兩條直徑AB,CD間夾角為60°,其中直徑AB水平,AD與CD是光滑的細桿.從A點和C點分別靜止釋放兩小球,從A,C點下落到D點的時間分別是t1,t2則t1∶t2=.
思考 本例中兩小球的運動雖然時間不相等,但處理方法和等時圓模型相同.首先根據牛頓運動定律分析所用時間與圓半徑之間的關系表達式,其次分別以AD,CD為直徑作圓,分析對應半徑比,從而得到所用時間比.
解析 由幾何關系可得,AD與水平面的夾角為30°,設圓周的半徑為R,則有xAD=2Rcos30°=3R.根據牛頓第二定律可得,小球在AD上運動的加速度大小為:a1=gsin30°=12g,根據xAD=12a1t21,可得t1=2xADa1=43Rg,由幾何關系可得xCD=2R,小球在CD上運動的加速度大小為a2=gsin60°=32g.根據xCD=12a2t22,可得t2=2xCDa2=8R3g,則有t1∶t2=3∶2.
4 結語
上述例題中,三個模型問題都體現出牛頓運動定律的應用和重要性,連接體模型主要體現牛頓運動定律與整體隔離思想的綜合應用,傳送帶模型主要是運用牛頓運動定律找到共速點再解題,等時圓模型則把牛頓運動定律應用在圓上.這些模型的熟悉和掌握,能幫助學生更高效地運用牛頓運動定律解決問題.
參考文獻:
[1]胡平.理想模型的建立過程——以課堂教學“牛頓運動定律的應用——瞬時性問題”為例[J].物理之友,2014(12):1-3+8.
[2]袁俊.連接體問題中的滑塊模型例析[J].中學物理,2014,32(01):66-67.
[3]褚祝文.基于新高考的高三復習課深度學習教學策略——以“牛頓運動定律的應用:板塊模型”為例[J].中學物理,2021,39(09):37-40.

