基于 BPNN-SVM-ELM 融合算法的氣化爐預測模型

摘要：基于遺傳算法-反向傳播神經(jīng)網(wǎng)絡（GA-BPNN）、遺傳算法-支持向量機（GA-SVM）、 極限學習機（ELM）單一數(shù)據(jù)驅(qū)動模型穩(wěn)定性差、信息熵線性融合模型建立時間成本高的問題， 提出了信息熵 Stacking 融合建模法。使用工廠實際生產(chǎn)數(shù)據(jù)，以氣化爐負荷、進料壓力與流 量、激冷水流量為輸入，以氣化爐出口溫度、水洗塔出口合成氣溫度與流量、合成氣組成為輸 出，建立了氣化爐的信息熵 Stacking 融合預測模型。結果表明：信息熵 Stacking 融合模型預測 項—氣化爐出口溫度、水洗塔出口合成氣溫度與流量、合成氣中 CO 含量與 H2 含量這 5 個參 數(shù)的平均相對誤差（MRE）分別為 1.89%、0.17%、0.78%、0.95% 與 0.71%，均表現(xiàn)良好且較 單一數(shù)據(jù)驅(qū)動模型更加穩(wěn)定，擬合速度較信息熵線性融合模型提升約 19%。模型可結合優(yōu)化算 法應用于氣化過程氧氣與煤漿流量比等操作條件的在線優(yōu)化以及氣化爐氣化溫度的優(yōu)化，從而 提高過程的有效氣產(chǎn)率。

關鍵詞：煤氣化；BPNN；SVM；ELM；Stacking 算法

中圖分類號：TP183

文獻標志碼：A

氣化爐內(nèi)高溫環(huán)境和測量手段的局限使得研究 者們無法僅通過實驗方法獲取影響爐內(nèi)氣化反應的 全部關鍵參數(shù) [1] ，因此極有必要通過模擬手段建立能 描述氣化爐內(nèi)復雜反應機理、克服實際生產(chǎn)中工藝 參數(shù)多變性的氣化爐數(shù)學模型。

目前廣泛應用的單一的氣化爐模擬模型主要有 機理模型和數(shù)據(jù)驅(qū)動模型[2-4]。由于機理模型在建立 過程中一般都會對氣化爐內(nèi)復雜的氣化過程進行一 定程度的簡化，加上煤氣化生產(chǎn)中實時入爐煤質(zhì)數(shù) 據(jù)的缺失，因而在實際應用中其準確度會不可避免 地降低。數(shù)據(jù)驅(qū)動模型因為具有擬合能力出色、對 機理知識依賴性低等優(yōu)點，被廣泛應用于煤氣化模 擬中，最常見的數(shù)據(jù)驅(qū)動模型有反向傳播神經(jīng)網(wǎng)絡 （BPNN）[5]、 支 持 向 量 機 （SVM）[6] 以 及 極 限 學 習 機 （ELM）[7]。單一的數(shù)據(jù)驅(qū)動模型雖然具有簡單快速的 優(yōu)點，但在穩(wěn)定性上一直存在些許問題[8]。針對上述 兩類單一模型存在的性能局限，研究者們提出了將 機理模型與數(shù)據(jù)驅(qū)動模型組合（即混合模型），以期 兩者性能互補的建模思路[9-11]。但由于此類模型仍要 借助于機理模型的建立，所以無法達到簡化過程、降 低模型對參數(shù)依賴度的目的。

數(shù)據(jù)驅(qū)動融合模型能通過組合多個同類或不同 類的包含不同信息的單一數(shù)據(jù)驅(qū)動模型[12] ，改善單一 數(shù)據(jù)驅(qū)動模型存在的穩(wěn)定性問題。黃煒等[13] 通過多 個數(shù)據(jù)驅(qū)動模型的智能組合，實現(xiàn)了對短期電力負 荷的準確預測。趙敏等[14] 對比了 SVM算法、長短期 記憶網(wǎng)絡（LSTM）算法、SVM-LSTM 融合算法識別 惡意軟件的能力，證明 SVM-LSTM 算法具有更高的 準確性，較單一數(shù)據(jù)驅(qū)動模型有更好的應用前景。

考慮到煤氣化生產(chǎn)中實時入爐煤質(zhì)和煤漿數(shù)據(jù) 的缺失，本文基于數(shù)據(jù)驅(qū)動融合算法，使用工廠實際 運行生產(chǎn)數(shù)據(jù)，提出組合信息熵線性融合法與 Stacking融合法，建立了 BPNN-SVM-ELM 的信息熵 Stacking 融合氣化爐模型。結果表明：Stacking 融合模型在準 確性、穩(wěn)定性以及擬合速率上具有優(yōu)勢，之后結合遺 傳算法 （GA），在實際工況其他輸入條件保持不變的 情況下，對氣化系統(tǒng)的氧氣流量進行了優(yōu)化計算，得 到了能提高氣化爐的有效氣產(chǎn)率的優(yōu)化參數(shù)。

1""" BPNN-SVM-ELM 融合模型

1.1 BPNN、SVM、ELM 的差異性比較

BPNN、SVM、ELM 模型目前已被廣泛應用于 工業(yè)軟測量領域中，其優(yōu)缺點與算法間的差異性也 得到了較為充分的證實。

BPNN 的擬合原理是經(jīng)驗風險最小化中的梯度 下降法，即通過梯度下降，逐漸逼近數(shù)據(jù)集的全局最 優(yōu)解，模型較易在梯度下降過程中陷入局部最優(yōu)解， 因而無法找到全局最優(yōu)解，影響模型準確性[15-17]。

SVM 的擬合原理是結構風險最小化，即在找尋 數(shù)據(jù)集全局最優(yōu)解的同時，加上一個懲罰項，約束模 型復雜度，抑制過擬合的出現(xiàn)，使得模型較經(jīng)驗風險 最小化所得擬合結果有更好的泛化能力，然而由于 復雜度低，模型對數(shù)據(jù)缺失問題較為敏感，降低了模 型的可靠性[18-20]。

ELM 的擬合原理是經(jīng)驗風險最小化中的最小二 乘法，即根據(jù)最小二乘法直接求出數(shù)據(jù)集的全局最 優(yōu)解。模型求解時隨機產(chǎn)生的權值和偏差可能使模 型部分節(jié)點失效，降低了模型的可靠性[21-22]。

各模型不同的擬合原理，使它們出現(xiàn)異常的原 因與表現(xiàn)也會有所不同。對 BPNN、SVM、ELM 這 3 種算法進行融合，可在一定程度上降低最終得到的 融合模型出現(xiàn)異常值的可能。

1.2 BPNN-SVM-ELM 信息熵線性融合模型

BPNN-SVM-ELM 信息熵線性融合模型 （LFM） 通過信息熵權重分配法線性組合 BPNN、SVM 和 ELM 完成模型建立（圖 1），具體步驟如下[23] ：

（1）數(shù)據(jù)處理。預處理數(shù)據(jù)，并劃分為訓練集 X1、驗證集 X2、測試集 X3。

（2）子模型建立與選擇。通過 X1 建立擁有不同 結構參數(shù)的子模型，之后依據(jù)各子模型對 X2 的預測 表現(xiàn)確定各子模型的最優(yōu)模型結構參數(shù) （如 BPNN 隱層神經(jīng)元數(shù)、SVM 核函數(shù)、ELM 隱層節(jié)點數(shù)），得 到 3 種最優(yōu)子模型 （如 BPNNOPT，SVMOPT，ELMOPT）。

（3）建立基于信息熵算法的線性融合模型。信 息熵是一個對數(shù)據(jù)集中數(shù)據(jù)穩(wěn)定性進行度量的參 數(shù)，模型預測數(shù)據(jù)集的預測誤差信息熵越大，預測一 致性越差，則預測表現(xiàn)越不穩(wěn)定。基于各子模型關 于 X2 的相對預測誤差求信息熵，以信息熵為依據(jù)計 算融合模型中各子模型的融合權重系數(shù)，具體求解 過程為：

最終通過 wj 對最優(yōu)子模型進行線性融合，并使 用 X3 考察其性能表現(xiàn)，但由于線性融合方式是通過 直接加權各子模型的輸出來實現(xiàn)，其擬合建立時間 是所有相同輸入輸出結構的子模型擬合耗時的疊 加，因而需要付出較高的時間成本。

1.3 BPNN-SVM-ELM 的信息熵 Stacking 融合模型

參考 Stacking 融合建模方式串聯(lián)一級學習模型 與次級學習模型（次級學習模型以一級學習模型的輸 出為輸入特征進行訓練并完成最終的預測）來提高 模型性能的思路，本文提出將信息熵線性融合法與Stacking 融合法組合，以 SVM-ELM 的信息熵線性融 合模型為一級學習模型，以 BPNN 模型為次級學習 模型，建立信息熵 Stacking 融合模型，通過降低擬合 速度最慢的 BPNN 模型的擬合復雜度的方式，在提 高數(shù)據(jù)驅(qū)動模型穩(wěn)定性的同時，減少融合模型建立 所需的時間成本，如圖 2 所示。具體過程如下：

（1）數(shù)據(jù)處理。將收集到的數(shù)據(jù)進行預處理后， 劃分為訓練集 X1、驗證集 X2、測試集 X3，之后進一步 將 X1 等分為多份 （以 5 份為例） 訓練子集 X11、X12、 X13、X14、X15。

（2）一級 SVM-ELM 線性融合模型的構建。挑 選 X12、X13、X14、X15 這 4 份訓練子集組成訓練集，分 別擬合建立 SVM 子模型與 ELM 模型，參照 1.2 節(jié)步 驟 ，通過考察子模型針對 X2 的預測表現(xiàn) ，挑選出 SVM 最優(yōu)子模型 SVM1 與 ELM 最優(yōu)子模型 ELM1， 通過式（1）～式（5）計算分配權重，組合最優(yōu)子模型 后 ， 建 立 SVM-ELM 信 息 熵 線 性 融 合 模 型 ， 記 為 LFM1，并使用模型 LFM1 對建立模型時余下的訓練 子集 X11 與測試集 X3 進行預測。挑選不同的訓練子集 進 行 組 合 （X11X13X14X15、 X11X12X14X15、 X11X12X13X15、 X11X12X13X14），重復上述步驟，得到 4 組基于不同訓練 集建立的融合模型 LFM2、LFM3、LFM4、LFM5，并 使用它們對訓練子集 X12、X13、X14、X15 與測試集 X3 進行預測。之后將模型 LFM1、LFM2、LFM3、LFM4、 LFM5 對訓練子集的預測結果組合，得到一級模型關 于 X1 的 預 測 結 果 （YLFM1）， 對 模 型 LFM1、 LFM2、 LFM3、LFM4、LFM5 關于 X3 的 5 次預測結果求平 均值，得到一級模型關于 X3 的預測結果 （YLFM2）。

（3）次級 BPNN 子模型的構建與最終預測。以 YLFM1 為訓練集，擬合建立多個擁有不同隱層神經(jīng)元 數(shù)的 BPNN 模型，以 YLFM2 為測試集，考察并比對各 BPNN 模型關于樣本集 YLFM2 的預測性能參數(shù)、確定 BPNN 次級模型的最優(yōu)隱層神經(jīng)元數(shù)，最后選定的次 級模型 BPNNOPT 關于樣本集 YLFM2 的輸出，即為最終 信息熵 Stacking 融合模型關于 X3 的預測輸出。

2""" 模型建立及應用

2.1 生產(chǎn)數(shù)據(jù)預處理與前期準備

本文的建模對象為頂置單噴嘴結構的 SE 水煤 漿氣化爐，氣化爐耐火襯里為耐火磚，爐膛容積 36.72 m3 ， 操作壓力 6.0 MPa，設計投煤量 1000 t/d，煤質(zhì)分析數(shù) 據(jù)見表 1。

收集 2021 年 1～3 月、9～11 月的實際運行數(shù)據(jù) 共 3794 組，其中包含氣化爐操作參數(shù)以及部分氣化 爐監(jiān)測變量（平均采樣周期為 1 h ）。根據(jù) 3-sigma 法 則，剔除數(shù)據(jù)樣本中的干擾點，即如果某樣本滿足式 （6），則將其從數(shù)據(jù)集中刪除：

式中：N 為樣本數(shù)量； 為樣本 i 的某項特征值； 為 所有樣本某項特征值的平均值； 為所有樣本某項特征值的標準差。

根據(jù)式（6）計算結果，去除掉 3794 組數(shù)據(jù)中存 在的 160 個干擾點后，從剩余的 3634 組樣本中隨機 抽取 1000 組樣本用于建立模型的樣本集，樣本集各 項數(shù)據(jù)的描述性統(tǒng)計值列于表 2～表 3。

按照 8∶1∶1 的比例，將樣本集初步劃分為訓 練 集 X1 （800 組 ）、 驗 證 集 X2 （100 組 ） 以 及 測 試 集 X3 （100 組）。樣本輸入特征為 6 項操作參數(shù)，輸出標 簽為 5 項監(jiān)測值，借助 Python 語言實現(xiàn)模型開發(fā)，同 時為了保證模型的可復現(xiàn)性，所有子模型的隨機數(shù) 種子皆設定為 1。

使用以下誤差參數(shù)評估模型性能，平均絕對誤 差（MAE）或平均相對誤差（MRE）反映模型的預測準 確性，均方根誤差（RMSE）反映模型的預測穩(wěn)定性， 決定系數(shù)（R 2 ）反映模型對所模擬過程的代表性。具 體計算公式如式（7）～式（10）所示：

使用測試集 X3 考察融合模型與各子模型的性 能表現(xiàn)，結果見表 7。表 7 表明，擬合原理間存在差 異，使得各子模型針對多項預測值的表現(xiàn)各有優(yōu) 劣。對于最小值為 996.52 的 T 值以及最小值為 38.4 的 xCO 值，GA-BPNN預測表現(xiàn)最佳，MAE 分別為 19.78 xH2 與 0.41；對于最小值為 228.12 ℃ 的 Tg，w 值，GA-SVM 子 模型的 MAE 最小（0.43）；對于最小值為 111894.9 Nm3 /h 的 Fg，w，以及最小值為 35.4 的 ，ELM 預測表現(xiàn)最 佳，MAE分別為 941.06 與 0.25。通過信息熵算法組 合 3 種子模型得到的線性融合模型（LFM），可以借助 各子模型預測值間的差異性，對它們進行一定程度 的中和與調(diào)節(jié)，在針對各項監(jiān)測值的預測中，融合模 型的 MAE 值、RSME值，都優(yōu)于或接近于當前預測 項的最優(yōu)子模型。同時對比表 4～表 7 中數(shù)據(jù)可以看 出，由于穩(wěn)定性問題，基于驗證集 X2 挑選的最優(yōu)子模 型應用于測試集 X3 數(shù)據(jù)的預測時，預測性能將出現(xiàn) 波動，融合模型則可以通過將它們組合來減弱這種 不確定性帶來的影響，提高模型的穩(wěn)定性。

2.3 信息熵 Stacking 融合模型的建立

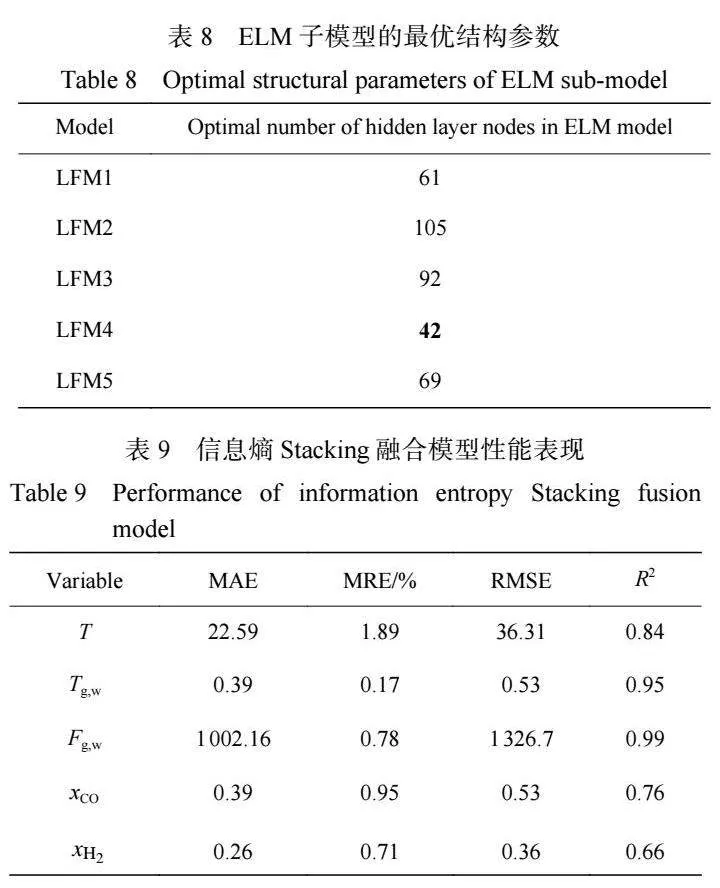
將包含 800 組樣本的訓練集 X1 等分成 5 份，得 到含 160 組樣本的訓練子集 X11、X12、X13、X14、X15。 參照 1.3 節(jié)步驟，選擇訓練子集中的 X12、X13、 X14、X15 4 項合并，得到包含 640 組樣本的樣本集，結合此樣本集與驗證集 X2，通過式（ 1） ～式（ 5）建立 SVM-ELM 的信息熵線性融合模型 LFM1，具體建立 過程類似 2.2 節(jié)。利用 LFM1 模型對訓練子集 X11、 測試集 X3 進行預測，模型的預測集數(shù)據(jù)規(guī)模分別為 5×160、5×100。重復此步驟，最終得到線性融合模型 LFM1、LFM2、LFM3、LFM4、LFM5，將它們關于訓 練子集 X11、X12、X13、X14、X15 的預測結果組合，得到 一級模型關于訓練集 X1 的最終預測集，數(shù)據(jù)規(guī)模 5×800；對它們關于測試集 X3 的預測結果求平均值， 得到一級模型關于測試集 X3 的最終預測集，數(shù)據(jù)規(guī) 模為 5×100。各線性融合模型的 SVM 子模型核函數(shù) 均選取 RBF，ELM 子模型的最優(yōu)結構參數(shù)描述見 表 8。

以一級模型關于訓練集 X1 的最終預測集為訓 練集，建立多個輸入神經(jīng)元數(shù)為 5、輸出神經(jīng)元數(shù)為 5、隱層神經(jīng)元數(shù)不等的 GA-BPNN 模型，以一級模 型關于測試集 X3 的最終預測集為測試集，確定 GA[1]BPNN 次級模型的最優(yōu)隱層神經(jīng)元數(shù)為 9，具體過程 參照 2.2 節(jié)，至此完成 Stacking 融合模型的建立。最 優(yōu) GA-BPNN 次級模型針對一級模型最終預測集的 預測輸出，即信息熵 Stacking 融合模型針對測試集 X3 的輸出，具體預測性能參數(shù)見表 9。

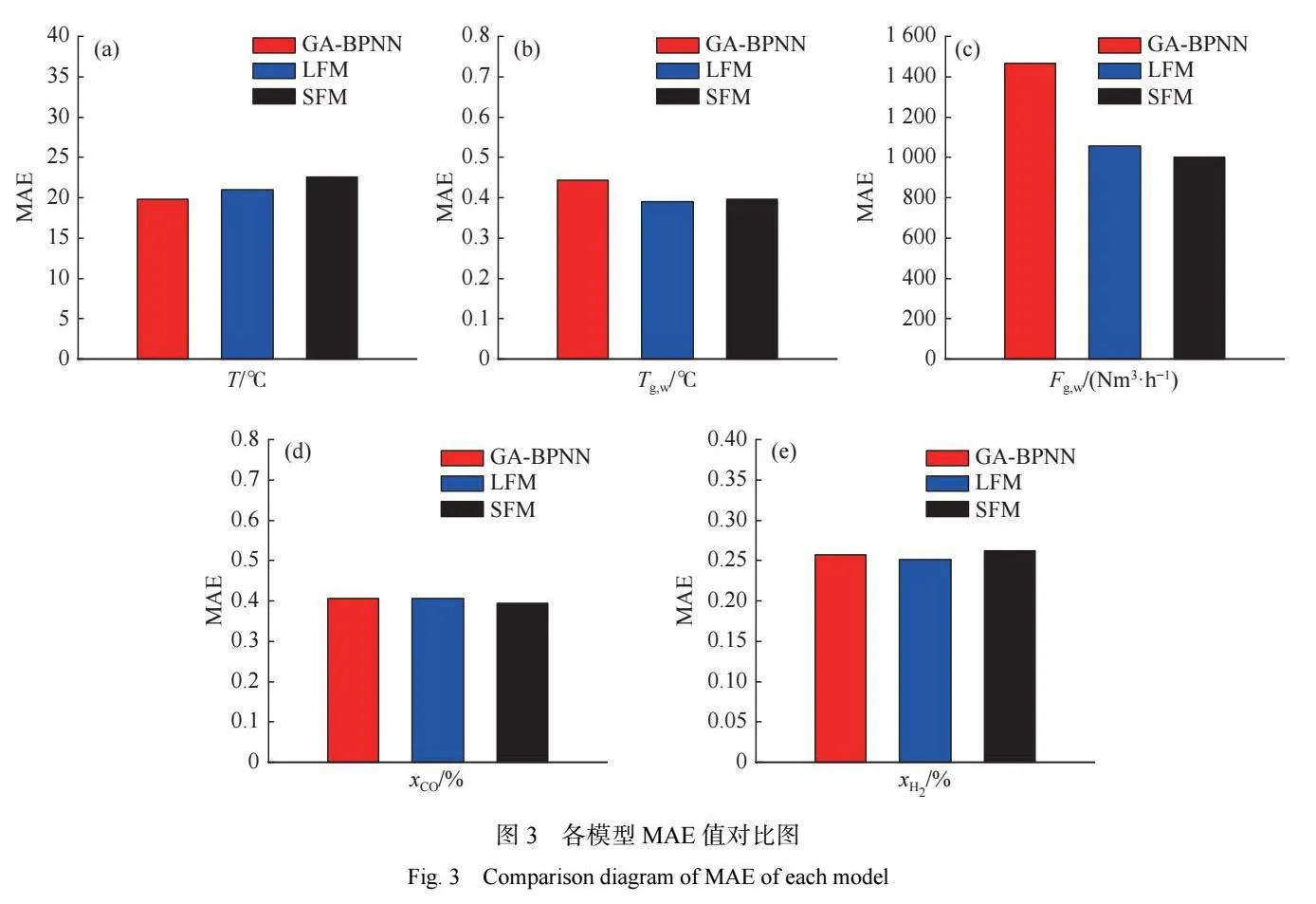
對比表 7、表 9 中不同模型關于測試集 X3 的預 測性能表現(xiàn)，以圖 3 中代表模型準確度的 MAE 值為 例 ，在針對 5 項預測值的預測中 ，信息熵 Stacking 融合模型 （SFM） 與信息熵線性融合模型 （LFM） 各有 優(yōu)劣，且都可以克服 GA-BPNN 模型在預測 Fg，w 時出 現(xiàn)的異常性能波動。在代表模型穩(wěn)定性的 RMSE 值 及其他性能參數(shù)上，也表現(xiàn)出相同的情況。

除了在預測表現(xiàn)上持平信息熵線性融合模型 外，信息熵 Stacking 融合模型的性能提升主要表現(xiàn)在 建立響應耗時上。如表 10 所示，由于將 GA-BP 神經(jīng) 網(wǎng)絡子模型的輸入特征數(shù)從 6 項降低到了 5 項，使得 信息熵 Stacking 融合模型的建立耗時較信息熵線性 融合模型降低了 19% 左右 ，同樣短于單一的 GA[1]BPNN 模型。

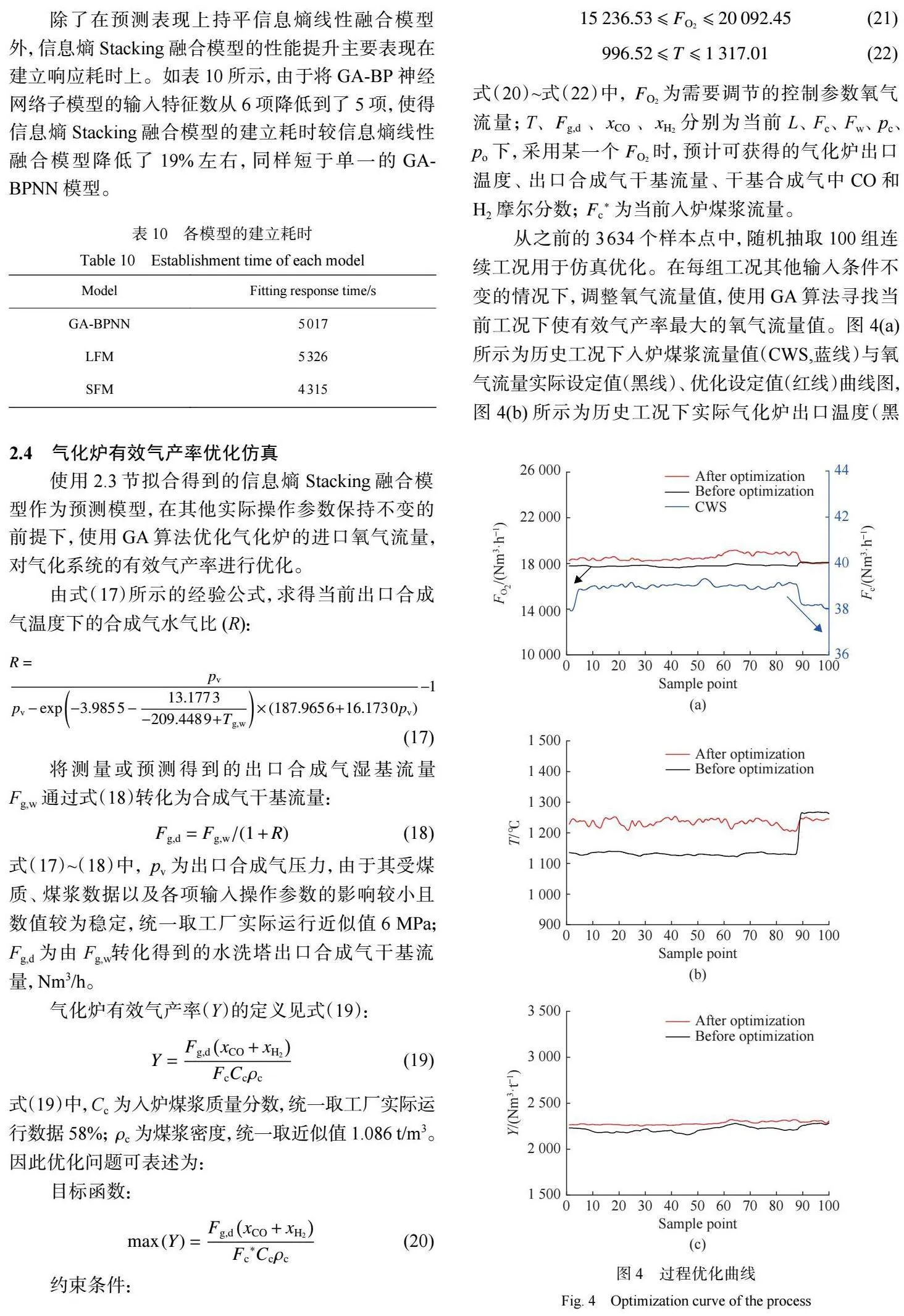
從之前的 3634 個樣本點中，隨機抽取 100 組連 續(xù)工況用于仿真優(yōu)化。在每組工況其他輸入條件不 變的情況下，調(diào)整氧氣流量值，使用 GA 算法尋找當 前工況下使有效氣產(chǎn)率最大的氧氣流量值。圖 4（a） 所示為歷史工況下入爐煤漿流量值（CWS，藍線）與氧 氣流量實際設定值（黑線）、優(yōu)化設定值（紅線）曲線圖， 圖 4（b） 所示為歷史工況下實際氣化爐出口溫度（黑線）與優(yōu)化后氣化爐出口溫度（紅線）曲線圖，圖 4（c） 所示為歷史工況下實際有效氣產(chǎn)率（黑線）與優(yōu)化后 有效氣產(chǎn)率（紅線）曲線圖。

圖 4 結果表明，優(yōu)化仿真可以通過改變氧氣流 量調(diào)節(jié)氧氣和入爐煤漿的流量比，優(yōu)化氣化溫度，提 高有效氣產(chǎn)率。以本次使用的 100 組工況為例，優(yōu)化 后的有效氣產(chǎn)率平均值從 2209.19 Nm3 /t 提高到了 2294.03 Nm3 /t，整體增幅 3.84%。

3""" 結 論

本文基于 GA-BPNN 模型、GA-SVM 模型、ELM 模型，組合信息熵權重分配法與 Stacking 融合法，建 立了氣化爐的信息熵 Stacking 融合模型，并比較了它 與信息熵線性融合模型和 3 個子模型的預測性能，得 出以下結論：

（1） 信息熵 Stacking 融合模型關于氣化爐出口溫 度、水洗塔出口合成氣溫度與流量、合成氣 CO 摩爾 分數(shù)、H2 摩爾分數(shù)的 MRE 值分別為 1.89%、0.17%、 0.78%、0.95% 與 0.71%，可以很好地繼承信息熵線性 融合模型的優(yōu)秀預測表現(xiàn)。

（2） 信息熵 Stacking 融合模型擬合響應速度較信 息熵線性融合模型提升了 19% 左右，應用于過程優(yōu) 化指導中時將更有優(yōu)勢。

（3） 基于能實時預測氣化爐出口參數(shù)的信息熵 Stacking 融合模型，結合 GA 算法對氣化爐穩(wěn)定運行 時的氧氣流量進行適當優(yōu)化調(diào)節(jié)，能在一定程度上 提高氣化爐的有效氣產(chǎn)率。

參考文獻：

SUN Z H， HOU Z S， YIN C K. Data driven modeling for UGI gasification process via a variable structure genetic BP neural network[C]//2014 International Joint Conference on Neural Networks. New York： IEEE， 2014： 1071-1078.

張志華， 白金鋒， 劉洋， 等. 煤炭氣化過程數(shù)學模型構建的 研究進展[J]. 煤炭科學技術， 2019， 47（11）： 196-205.

SUN Z H， DAI Z H， ZHOU Z J， et al. Numerical simula[1]tion of industrial opposed multi-burner coal-water slurry en[1]trained" flow" gasifier[J]." Industrial" amp;" Engineering" Chemi[1]stry Research， 2012， 51（6）： 2560-2569.

WU H C， YANG C， ZHANG Z L. Simulation of two-phase flow" and" syngas" generation" in" biomass" gasifier" based" on two-fluid model[J]. Energies， 2022， 15（13）： 4800.

杜旭鵬， 王鈺琪， 許建良， 等. 基于數(shù)據(jù)驅(qū)動的氣化爐出口 溫度在線測量[J]. 華東理工大學學報（自然科學版）， 2023， 49（2）： 168-175.

ALI B， RAMESH K A， HANI H S， et al. Elucidating the effect of process parameters on the production of hydrogen[1]rich syngas by biomass and coal co-gasification techniques： A multi-criteria modeling approach[J]. Chemosphere， 2022， 287： 1-12.

LI X， NIU P F， LI G Q， et al. An adaptive extreme learning machine for modeling NOx emission of a 300 MW circulat[1]ing fluidized bed boiler[J]. Neural Process Letter， 2017， 46： 643-662.

LIU S K， YANG Y， YU L J， et al. Predicting gas produc[1]tion by" supercritical" water" gasification" of" coal" using"" ma[1]chine learning[J]. Fuel， 2022， 329： 125478.

VISWANATHAN K， ABBAS S， WU W， et al. Syngas ana[1]lysis" by" hybrid" modeling" of" sewage" sludge" gasification" in downdraft" reactor：" Validation" and" optimization[J]. Waste Management， 2022， 144： 132-143.

DENG Y S， AVILA C， GAO H J， et al. A hybrid modeling approach to estimate liquid entrainment fraction and its un[1]certainty[J]." Computers" amp;" Chemical" Engineering，" 2022， 162： 107796.

WILLIS M J， VON S M. Simultaneous parameter identifi[1]cation and discrimination of the nonparametric structure of hybrid" semiparametric" models[J]." Computers" amp;" Chemical Engineering， 2017， 104： 366-376.

王佳晨. 多模型融合建模方法研究及其在化學中的應 用[D]. 杭州： 浙江工業(yè)大學， 2020.

黃煒， 陳田. 基于SAE與CEEMDAN-BiLSTM組合模型的 短期電力負荷預測[J]. 計算機應用與軟件， 2022， 39（7）： 52-58.

趙 敏， 張雪芹， 朱唯一， 等. 基于LSTM-SVM 模型的惡意 軟件檢測方法[J]. 華東理工大學學報（自然科學版）， 2022， 48（3）： 677-684.

LU" C" Y，" SHI" J." Relative" density" prediction" of" additively manufactured" Inconel" 718：" A" study" on" genetic" algorithm optimized" neural" network" models[J]. Rapid" Prototyping Journal， 2022， 28（8）： 1425-1436.

KUANG" F" L，" LONG" Z" L，" KUANG" D" M， et al. Applica[1]tion of back propagation neural network to the modeling of slump" and" compressive" strength" of" composite geopolymers[J]. Computational" Materials" Science，" 2022， 206： 111241.

WEN" H" Q，" YANG" S，" WANG" Z" H， et al." A" systematic modeling methodology of deep neural network-based struc[1]ture-property" relationship" for" rapid" and" reliable" prediction on flashpoints[J]. AIChE Journal， 2022， 68（1）： 1-15.

LING" H，" QIAN" C，" KANG" W， et al. Combination" of" sup[1]port vector machine and K-fold cross validation to predict compressive strength of concrete in marine environment[J]. Construction and Building Materials， 2019， 206： 355-363.

ZHOU T， LU H， WANG W W， et al. GA-SVM based fea[1]ture selection and parameter optimization in hospitalization expense" modeling[J]. Applied" Soft" Computing，" 2019，" 75： 323-332.

JAIR C， FARID G L， LISBETH R M， et al. A comprehens[1]ive survey on support vector machine classification： Appli[1]cations，" challenges" and" trends[J]. Neurocomputing，" 2020， 408： 189-215.

LI D Z， LI S， ZHANG S B， et al. Aging state prediction for supercapacitors based" on" heuristic" kalman" filter"" optimiza[1]tion" extreme" learning" machine[J]. Energy，" 2022，" 250： 123773.

RAJA M" N" A，" SHUKLAnbsp; S" K." An" extreme" learning"" ma[1]chine model for geosynthetic-reinforced sandy soil founda[1]tions[J]. Proceedings" of" the" Institution" of" Civil" Engineers[1]Geotechnical Engineering， 2022， 175（4）： 383-403.

XIA" L" Y，" WANG" J" C，" LIU" S" S， et al." Prediction" of" CO2 solubility" in" ionic" liquids" based" on" multi-model" fusion method[J]. Processes， 2019， 7（5）： 1-16.

SU Y， JIN S M， ZHANG X P， et al. Stakeholder-oriented multi-objective process optimization based on an improved genetic" algorithm[J]." Computers" amp;" Chemical" Engineering， 2019， 132（4）： 1-16.