基于鄰域依賴度融合信息熵屬性約簡

李朝清 孫潔 原頔 李毅

摘要：鄰域粗糙集是經典粗糙集理論的一個重要擴展，它已成功應用于諸多領域，其中屬性約簡是其最主要的應用之一。鄰域依賴度與信息熵是鄰域粗糙集中的重要內容，鄰域依賴度屬則是通過識別出那些對決策屬性具有顯著依賴關系的屬性，鄰域信息熵可以用來衡量條件屬性對決策屬性的重要性。通過它們構建約簡算法可以消除數據集中的冗余信息，提高數據處理和分析的效率。基于此，本文以鄰域依賴度融合信息熵為基礎，提出了基于鄰域依賴度融合信息熵屬性約簡算法。使用公開數據集，實驗結果表明該算法可以選擇較少的屬性來保持或提高聚類算法的性能，這充分證明了該算法具有較強的有效性。

關鍵詞：屬性約簡；鄰域依賴度；鄰域信息熵

中圖分類號：TP311? ? ?文獻標識碼：A

文章編號：1009-3044（2024）07-0028-05

開放科學（資源服務）標識碼（OSID）

0 引言

屬性約簡（Attribute Reduction） [1]是數據預處理的一個重要步驟，通常在數據挖掘、機器學習、模式識別等領域中使用。其核心目的是識別并移除數據中的不相關的、冗余的或不重要的屬性（特征），以便減少特征空間的維度并簡化后續的分析或模型學習過程。這項技術不僅可以降低高維空間數據的復雜性，還可以提高數據處理的效率。屬性約簡的研究和應用一直是數據科學領域活躍的研究方向，科研工作者不斷提出新技術和算法以適應不斷增長和變化的數據分析需求。

粗糙集理論（Rough Set Theory） [2]是由Pawlak在1980年初提出，是一種處理不確定性和不完整信息的數學工具。該理論廣泛應用于數據挖掘、模式識別和人工智能等領域，特別在屬性約簡方面展示了其有效性。經典粗糙集理論的應用限于標稱型數據，而非數值型數據。但在現實生活中的數據集通常為，為了將數值型數據納入粗糙集分析，一個常見的做法是離散化，但是，離散化處理通常是導致數據信丟失的重要原因。為了有效處理數值型數據。Lin等人提出了鄰域粗糙集的概念，Hu等人針對鄰域粗糙集理論進行了廣泛的討論和研究，并提供一種有效的工具來克服離散化處理[3-4]。

信息熵起源于信息論[5]，它是一種能夠建立衡量不確定性競爭機制的方法。Hu等人在傳統信息熵的基礎上，將其拓展到鄰域粗糙集，提出了鄰域信息熵的概念[4]。Chen等人進一步發展了鄰域信息熵理論，提出了一種有效的基于鄰域信息熵的不確定性度量方法。迄今為止，鄰域信息熵已被成功應用于屬性約簡[6]。

基于此本文提出了基于鄰域依賴度及信息熵的屬性約簡算法。

1 鄰域粗糙集理論

本節將回顧本文后續章節中關于鄰域粗糙集理論的一些定義及符號。

定義1[1，4]信息系統（Information System，IS）可以用一個四元組來表示，即[IS=（U，A，V，f）]。其中：[U={x1，x2，...，xn}]是非空有限對象集，稱為論域；[A]為屬性集，它是一個非空有限集；[V=a∈AVa]，[Va]為屬性[a]的值域；[f：U×A→V]是一個信息函數，它滿足對[?xi∈U（1≤i≤n）]及[?a∈A]有[f（xi，a）∈Va]。對于決策信息系統（Decision System，DS），屬性[A]可以分為2個互不相交的子集：條件屬性子集[C={c1，c2，...，cm}]和決策屬性集[D]，[C?D=?]，[C?D=A]。決策信息系統可以簡記為[DS=（U，C?D，V，f）]。

通過信息函數[f]定義不可區分關系。

定義2[1，4]給定一個信息系統[DS=（U，C?D，V，f）]，對[?B?C]，關于屬性子集[B]的不可區分關系[IND（B）]可定義為：

[IND（B）={（xi，xj）∈U×U|f（xi，ck）=f（xj，ck），?ck∈B}]? （1）

顯然，等價關系僅使用于標稱型數據集。

為了處理數值型數據集，本文將引入距離函數來構建鄰域信息系統。

定義3[1，4]給定一個[DS=（U，C?D，V，f）]對[?xi，xj，xp∈U] [（1≤i，j，p≤n）] ，假設[B={ck1，ck2，...，ckh}（1≤h≤m）?C]，距離函數[ΔB（xi，xj）]需要滿足如下關系：

[（1）ΔB（xi，xj）≥0，ΔB（x，y）=0當且僅當x=y（非負性）;（2）ΔB（xi，xj）=ΔB（xj，xi）（對稱性）;（3）ΔB（xi，xp）≤ΔB（xi，xj）+ΔB（xi，xp）（傳遞性）。]

[ΔB（xi，xj）]計算對象[xi，xj]在屬性子集[B]下的距離函數。本文采用歐式距離函數，即：

[ΔB（xi，xj）=（l=1h（f（xi，ckl）-f（xj，ckl））2）12]? ?（2）

其中，[f（xi，ckl）]與[f（xj，ckl）]分別表示對象[xi]與[xj]在屬性[ckl]下的屬性值。

基于距離函數并引入鄰域半徑[ε（ε≥0）]來粒化論域，形成鄰域關系和鄰域類。

定義3[1，4]給定一個[DS=（U，C?D，V，f）]，對[?xi∈U]， [ε≥0]， [?B?C]，那么[xi]在屬性子集[B]上的[ε-]鄰域定義為：

[nεB（xi）={xj|ΔB（xi，xj）≤ε，xj∈U}]? （3）

性質1[1，4] 對于[?xi，xj∈U]，有定義3可以得到[ε-]鄰域具有如下性質：

[（1）nεB（xi）≠?;（2）xj∈nεB（xi）?xi∈nεB（xj）;（3）i=1nnεB（xi）=U。]

定義4[1，4]給定一個[DS=（U，C?D，V，f）]，對[?B?C]，[ε≥0]，那么鄰域關系[nrεB]定義如下：

[nrεB={（xi，xj）|xi，xj∈U且xj∈nεB（xi）}]? （4）

由此可見，鄰域關系實際上刻畫了論域[U]中對象之間的相似性和不可區分性。

定義5[1，4]給定一個決策信息系統[DS=（U，C?D，V，f）]，對[?B?C]及[ε≥0]，[U/nrεB]構成[U]的鄰域覆蓋，稱其為[U]上的一個鄰域知識。其中，每個鄰域稱為一個鄰域知識或鄰域類。

基于給定距離函數和鄰域半徑來構建鄰域信息系統。

定義6[1，4]給定一個[DS=（U，C?D，V，f）]對[?B?C]和[ε≥0]，[nrεB]為屬性子集[B]導出的[U]上[B-ε]鄰域關系：[NRεC={nrεB}]為[U]上全體鄰域關系全體，稱四元組[NIS=（U，NRεC，V，f）]為鄰域信息系統。相應地，[NDS=（U，NRεC?D，V，f）]稱為鄰域決策信息系統。

在鄰域信息系統中可以定義相關的上下近似集，其相關定義如下。

定義7[1，4]給定一個[NIS=（U，NRεC，V，f）]，對[X?U]，[nrεB∈NRεC]，那么[X]基于鄰域關系[nrεB]的上近似集[nrεB（X）]與下近似集[nrεB（X）]分別定義為：

[nrεB（X）={xi|nεB（xi）?X≠?，xi∈U}]? （5）

[nrεB（X）={xi|nεB（xi）?X，xi∈U}]? （6）

其中，稱[POSnrεB（X）=nrεB（X）]為[X]的[nrεB]正域，稱[NEGnrεB（X）=U-nrεB（X）]為[X] 的[nrεB]負域，稱[BNDnrεB（X）=nrεB（X）-nrεB（X）]為[X]的[nrεB]邊界域。

基于上述鄰域粗糙集理論相關知識，還可以定義一些有實際應用價值的概念，如鄰域信息熵。

定義8[5]給定一個[NIS=（U，NRεC，V，f）]，鄰域關系[nrεB∈NRεC]確定的鄰域知識為[U/nrεB={N1，N2，...，Nq}]。那么，鄰域關系[nrεB]所關聯的鄰域信息熵[NEε（B）]可以定義為：

[NEε（B）=-i=1qNiUlog2NiU] （7）

其中，[NiU]為鄰域知識元素[Ni]對于論域[U]的隸屬度概率。

2 基于鄰域依賴度融合信息熵屬性約簡

在本節中，首先建議鄰域依賴度融合信息熵屬性選擇模型，接著提出了一種基于鄰域依賴度融合信息熵屬性選擇模型，然后基于具體模型對其進行分析。此外，還設計了相應的屬性約簡算法。

2.1 基于鄰域依賴度融合信息熵屬性選擇模型建立

給定一個[NIS=（U，NRεB，V，f）]，條件屬性集[C={c1，c2，...，cm}]。設[B={ck1，ck2，...，ckh}][（1≤h≤m）] ，且[B?C]，對[?xi，xj∈U] 在屬性子集[B]下的領域關系可以用[rBij]來表示如下：

[rBij=1，ΔB（xi，xj）≤ε;0，ΔB（xi，xj）>ε.]? ?（8）

從公式（8） 可以看出，當對象[xi]與[xj]之間的距離小于等領域半徑[ε]時，認為它們的領域相似度為1；大于領域半徑[ε]時；認為它們的相似度為0.其中鄰域半徑[ε]是可以調的。[nrεB]是[U]上關于[B]的鄰域關系，則鄰域關系矩陣[MnrεB]表示如下：

[MnrεB=rB11rB12…rB1nrB21rB22…rB2n????rBn1rBn2…rBnn]? （9）

由此可見，在屬性[B]下，[U]中對象[xi]的[ε-] 領域可以表示成[0-1]向量形式，即[nεB（xi）=（rBi1，rBi2，...，rBin）]。

定義9 決策[D]相對于條件[B]的鄰域正域的定義如下：

[POSεB（D）=X∈UnrεB（X）]? （10）

鄰域正域定義了決策[D]相對于條件[B]的變精度領域下近似集的并。

定義10 決策[D]相對于條件[B]的鄰域正域的定義如下：

[γεB（D）=|POSεB（D）|U]? （11）

定義11 如果[γεB（D）=γεB-{b}（D）]，稱[b]在[B]中是冗余的；否則，稱[b]在[B]是必要的。如果[B]中每一個屬性都是有必要的，則稱[B]是獨立的。

定義12 假設給定[B?C]，如果[B]滿足條件：

[（1）γεB（D）=γεC（D）;（2）?b∈B，γεB-{b}（D）<γεB（D），]

定義13 [?b∈C-B]，把[b]相對于[B]的重要度定義為：

[IMP（b，B，D）=γεB?{b}（D）-γεB（D）]? （12）

由于[0≤γεB（D）≤1]且[γεB?{b}（D）≥γεB（D）]，有[0≤IMP（b，B，D）≤1]。如果[IMP（b，B，D）=0]，則稱屬性[b]在[B]中冗余；否則稱[b]是必要的。

則稱[B]是[C]的一個約簡集。

在上述定義中，條件（1）要求約簡不能降低系統的區分能力，約簡后的條件屬性與全部的條件屬性具有相同的區分能力。條件（2）要求在屬性約簡后條件屬性中不存在多余的條件屬性，所有的條件屬性都是必要的。

2.2 基于鄰域依賴度融合信息熵選擇算法

到目前為止，本文已經建立了鄰域依賴融合信息的選擇模型，稱為“基于鄰域依賴度融合信息屬性約簡算法”。接下來，本小節將分析一個特定的基于鄰域依賴度融合信息熵的屬性約簡算法。

在基于鄰域粗糙集模型的數據處理中，通常需要對數據集進行歸一化處理，其計算模型如下：

[F（f（xi，ck））=f（xi，ck）-minckmaxck-minck]? （13）

其中，[f（xi，ck）] 為對象[xi]在條件屬性[ck]下對應的值，[maxck]和[minck]分別是論域[U]中對象關于條件屬性[ck] 下的最大值和最小值。歸一化后，這些屬性的屬性值取值范圍為[0，1]。

算法：基于鄰域依賴度融合信息熵屬性約簡算法（NDIEAR）

輸入：[DIS=（U，NRεC?D，V，f）]，其中[|C|=m]，鄰域半徑參數[ε]

輸出：一個約簡集[red]

1） 初始化[red←?，B←C-red]

2） 計算每個條件屬性[ck∈C]的鄰域信息熵[NEε（{ck}）]

3） 選擇最大的鄰域信息熵[NEε（{ck}）]，選擇屬性[ck]，即[red={ck}]

4） 當[B≠?]時

5） 對[?ckj∈B]

6） 計算屬性[ckj]的重要度[IMP（ckj，red，D）=γεred?{ckj}（D）-γεred（D）]

7） end

8） 選擇屬性[ckj']，使得[IMP（ckj'，red，D）=max（IMP（ckj，red，D）]

9） 如果[IMP（ckj'，red，D）>0]

10） [red=red?{ckj'}]

11） else

12） break

13） end

基于鄰域依賴度融合信息熵屬性約簡算法以空集為起點，首先，計算每個條件屬性的鄰域信息熵，選擇最大的鄰域信息熵的屬性加入約簡集合。接著，每次計算全部剩余屬性的屬性重要度，從中選擇重要度值最大的屬性加入約簡集合中，一直到所有剩余屬性重要度為0。算法的時間復雜度主要集中在步驟6-8中，計算所有對象鄰域依賴度。分析算法可知，鄰域依賴度的計算在最壞情況下的時間復雜度為[O（n2）]。假設系統中有[n] 個樣本，[m] 個條件屬性，約簡屬性子集有[q]個屬性。在步驟6中需要計算每個對象在不同屬性下的鄰域依賴度，其時間復雜[O（mn2+（m -1）n2+...+（m - q）n2）= O（12（2m - q）（q +1）n2）]。

3 實驗及分析

本節通過在聚類任務中的性能來評估VPNDAR算法，主要包括實驗數據集、實驗方案、實驗結果、參數分析等內容。

3.1 實驗數據集

從公開數據庫中選取6個數值屬性數據進行實驗。對于某些數據集中的缺失值，采用最大概率值法來填充缺失值，即用該屬性上其他樣本上出現頻率最高的值來填充缺失的屬性值。用于聚類的數據集描述如表1。

3.2 實驗方案

本文所提基于變精度鄰域依賴度屬性約簡（NDIEAR）算法作用于表1列出的數據集為每一個數據集選擇一個最優的屬性子集。

對于聚類實驗中，本文調用k-Means和FCM（Fuzzy C-Means）聚類算法來評估算法的性能。聚類算法返回數據集的預測決策，本節使用聚類準確率（ACC）來評估聚類算法的性能。其定義如下：

[ACC=i=1nδ（f（xi），f'（xi））n]? （14）

其中，[f（xi）]表示[xi]的真實決策屬性值，[f'（xi）]為[xi]的預測決策屬性值。如果[f（xi）=f'（xi）]，則[δ（f（xi），f'（xi））=1]。反之，則等于0。一個聚類算法的ACC值越大，說明其性能越好。由于k-Means和FCM聚類算法具有隨機性，所以重復實驗10次。最后，使用聚類ACC值的平均值和標準差來作為最終的結果。

NDIEAR算法，計算鄰域半徑[ε]在[0.1，1]步長為0.1的最優結果。同時，對于NDIEAR算法，通過大量實驗表明對于數值屬性數據集，通常很難達到以所有剩余屬性的重要度為0的停止條件。因此本文設置重要度停止條件為0.000 1。

3.3 實驗結果分析

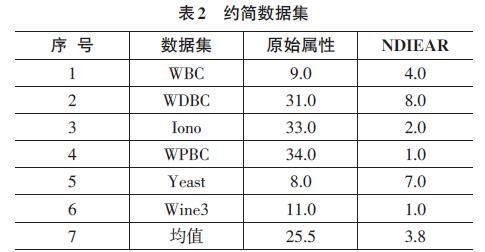
本節首先給基于鄰域依賴度融合信息熵屬性約簡結果，如表2所示。

表2給出了k-Means和FCM聚類算法的平均最優屬性個數。NDIEAR算法選擇的屬性數在所有數據集上均小于原始數據節屬性個數。例如，對于WDBC、Iono、WPBC及Wine3數據集而言，NDIEAR算法選擇的平均屬性個數為8.0、2.0、1.0及1.0，明顯小于原始屬性個數。此外，對于屬性數均值而言，NDIEAR算法遠小于原始屬性個數。

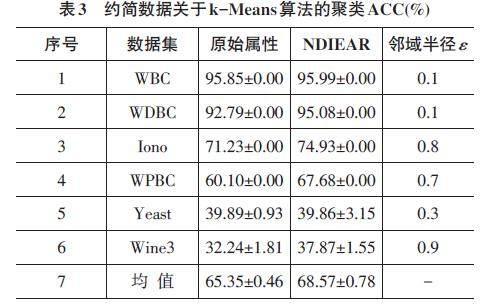
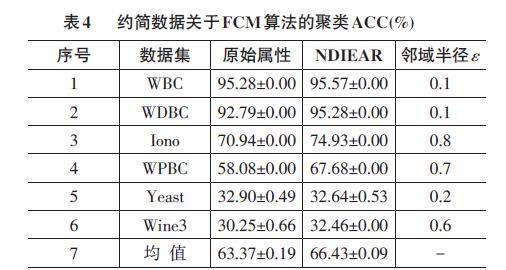
接下來，分別給出約簡數據關于聚類算法的聚類ACC（%）。如表3和表4所示。

表3和表4分別給出了基于k-Means算法和FCM算法的最優聚類ACC的結果。其中，粗體部分顯示最優值。通過表3和表4中的結果，得到一些相應的分析如下：

1） NDIEAR算法相比原始屬性有10種情形達到了最好的聚類ACC，而原始屬性只有2種情形。

2） 從ACC的均值來看，所提NDIEAR算法在兩種聚類算法中都取得了比較高的均值。

綜上所述，本文所提NDIEAR算法獲得了較好的聚類性能。它可以選擇較小的屬性子集，同時能保持或者提高聚類ACC。因此，NDIEAR算法適用于在聚類任務中的數值屬性約簡。

3.4 實驗參數分析

鄰域半徑參數[ε] 在NDIEAR算法中起著至關重要的作用，它可以用于控制數據分析的鄰域粒度，最終影響約簡的結果。

接下來，本文將給出不同鄰域半徑[ε]下約簡屬性數和平均聚類準確率曲線，如圖1所示。

NDIEAR算法，可以通過調整鄰域半徑參數ε在每個數據集上得到不同的屬性子集。圖1描述了不同鄰域半徑參數ε約簡屬性數和平均聚類準確率曲線。接下來，本文將從屬性約簡的個數和聚類ACC兩個方面進行分析。

通過分析圖1，可以看到，在一些數據集上隨著鄰域半徑參數ε的增加，約簡屬性的個數先保持平穩，接著逐漸降低，最后保持相對平穩，如Yest和Wine3。大部分數據集隨著變精度閾值[ε]的增加，約簡屬性的個數大體上呈逐增加的趨勢到達某個峰值，然后逐漸減少，如WBC、WDBC、Iono及WPBC。

在平均聚類準確方面，從圖1可知，對于大多數數據集，在多個鄰域半徑[ε]下可以取得高平均聚類精度。對于每個數據集，可以根據圖1選擇合適的鄰域半徑[ε]。因此，使用NDIEAR算法進行屬性約簡是可行的。

4 結論

本文設計了相應的NDIEAR算法。從公開數據庫中選取6個數據在所提NDIEAR算法上進行實驗。實驗結果表明，該算法可以選擇較少的屬性來保持或提高學習算法的能力。

參考文獻：

[1] 徐波.鄰域粗糙集的啟發式屬性約簡算法研究[D].成都：四川師范大學，2019.

[2] PAWLAK Z.Rough sets[J].International Journal of Computer & Information Sciences，1982，11（5）：341-356.

[3] HU Q H，YU D R，LIU J F，et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences，2008，178（18）：3577-3594.

[4] 胡清華.混合數據知識發現的粗糙計算模型和算法[D].哈爾濱：哈爾濱工業大學，2008.

[5] 袁鐘.混合數據無監督知識發現的模糊粗糙計算方法研究[D].成都：西南交通大學，2022.

[6] CHEN Y M，WU K S，CHEN X H，et al.An entropy-based uncertainty measurement approach in neighborhood systems[J].Information Sciences，2014，279：239-250.

【通聯編輯：梁書】