一道雙中點(diǎn)幾何題的多角度解答

高亮榮

【摘要】添加輔助線是解答幾何題的一個(gè)基本策略，要求對(duì)題目的重要條件作分析，對(duì)基本圖形進(jìn)行理解與聯(lián)系，運(yùn)用圖形之間的關(guān)聯(lián)探索思考問(wèn)題.下面以一道雙中點(diǎn)問(wèn)題作解題分析．

【關(guān)鍵詞】初中數(shù)學(xué)；輔助線；解題技巧

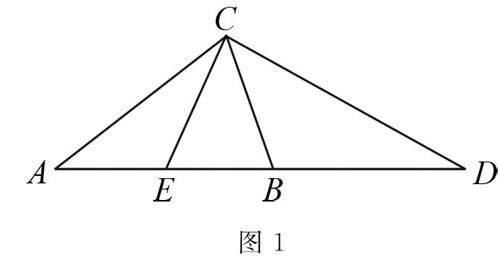
例題 如圖1，已知在△ABC中，AB=AC，CE是AB邊上的中線，延長(zhǎng)AB至點(diǎn)D，使BD=AB．求證：CD＝2CE．

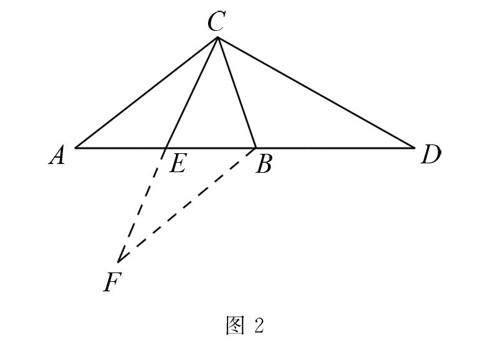
解析1 因?yàn)镃E是中線，如圖2.

延長(zhǎng)CE至點(diǎn)F，使EF=EC，這樣出現(xiàn)CF＝2CE，只要證明CF＝CD即可，連接BF，聯(lián)系已知條件，圖形中有全等三角形.

易得△EAC≌△EBF（SAS）．

則BF=AC=AB =BD，∠EBF=∠A．

又∠ABC=∠ACB，

所以∠FBC=∠FBE+∠EBC=∠A+∠ACB=∠DBC，

所以△FBC≌△DBC（SAS），

即CD=CF=2CE．

點(diǎn)評(píng) 上述輔助線是典型的“中線倍長(zhǎng)”法．由中點(diǎn)的條件，將中線延長(zhǎng)一倍，證明△EAC≌△EBF，并利用全等的結(jié)論，證明△FBC≌△DBC.

同樣的方法，延長(zhǎng)CE到點(diǎn)F，使得EF= CE，連接AF，證明△AEF≌BEC，△CAF≌△DBC．

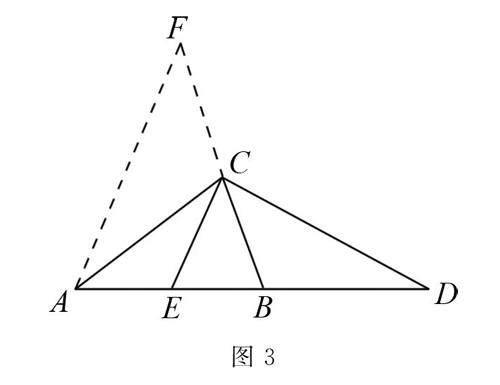
解析2 因?yàn)镃E是中線，則點(diǎn)E是AB的中點(diǎn)，如圖3.

可以在BC的延長(zhǎng)線上截取CF=CB，構(gòu)成三角形的中位線，得到AF＝2CE，只需求證AF＝CD.

AF與CD分別在△FCA和△CBD中，

易得FC=CB，AC=AB =DB，

由鄰補(bǔ)角得∠FCA =180°-∠ACB，

∠CBD=180°-∠ABC，

又AB=AC，則∠ACB=∠ABC．

所以△FCA≌△BCD（SAS）．

點(diǎn)評(píng) 上述的輔助線立足于“點(diǎn)E是AB的中點(diǎn)”，延長(zhǎng)三角形的另一邊，構(gòu)成三角形的中位線，并證明△FCA≌△BCD.

同樣的方法，如圖4.

延長(zhǎng)AC至點(diǎn)F，使CF=AC．連接BF，DF．

所以AF=2AC=2AB=AD．

因?yàn)锳C=AB，∠A=∠A，AD=AF，

所以△ABF≌△ACD（SAS）．

所以BF=CD．

因?yàn)镃E是△ABF的中位線．

所以CE=1/2BF=1/2CD．

所以CD=2CE．

結(jié)語(yǔ)

對(duì)一個(gè)陌生問(wèn)題，認(rèn)真審題是解題的基礎(chǔ)，可以由已知向結(jié)論推理，或由結(jié)論向已知推證；或者從兩邊向中間追尋，尋找已知與結(jié)論之間的橋梁．由題目的已知條件能夠挖掘出什么重要結(jié)論？由條件能聯(lián)想到什么？由結(jié)果還能聯(lián)想到什么？如本題重要的條件只有兩個(gè)：（1）等長(zhǎng)線段AB=AC；（2）在同條線段上的兩個(gè)中點(diǎn).從不同角度去思考，會(huì)產(chǎn)生不同的思考途徑，所用的基礎(chǔ)知識(shí)和方法也就不同，如解析一是基于“E是AB邊中點(diǎn)”，采取“中線倍長(zhǎng)”法，證明兩個(gè)三角形全等進(jìn)行解答，方法經(jīng)典且適用.解析2，利用“E是AB中點(diǎn)”，將三角形的另一邊倍長(zhǎng)，使CE為新三角形的中位線.解析3，利用“點(diǎn)B為AD中點(diǎn)”的條件，通過(guò)作三角形另一邊中點(diǎn)，構(gòu)成三角形的中位線.后面幾種輔助線的視角獨(dú)特，運(yùn)用中點(diǎn)的條件構(gòu)造三角形中位線，獨(dú)辟蹊徑，體現(xiàn)了創(chuàng)新思維的運(yùn)用，也培養(yǎng)了學(xué)生理性思考的能力.