基于SBM-GML 與面板門檻效應的碳排放強度與綠色全要素生產率的關系研究

王希泉WANG Xi-quan

（南京中醫藥大學衛生經濟管理學院，南京 210018）

0 引言

黨的二十大報告進一步提出深化中國式現代化和綠色低碳發展的戰略要求，為了追求高質量發展，工業綠色全要素生產率的提升有利于兼顧經濟發展與環境保護，轉變原有的高投入高污染，但是低效益的不利局面，因此加快綠色全要素生產率創業，可以更好地實現雙碳目標，實現經濟社會和人的高質量可持續發展。

綠色全要素生產率的研究是建立在全要素生產率的基礎上，具體體現為綠色發展這一綠色的本質特征，反映在工業綠色全要素生產率的研究中，需要在柯布-道格拉斯生產函數的基礎上，考慮資本和勞動等投入要素的綠色特征，同時由于以往的研究在綠色全要素生產率的生產函數設定中忽略了空間溢出性，因此本文設定的模型也考慮了空間溢出性和空間權重矩陣的情形[1，2]。

1 理論機制與命題假說

1.1 綠色全要素生產率的相關研究

學術界對綠色全要素生產率的關注始于勞動生產率的研究，郭愛君和范巧（2022）認為，綠色全要素生產率與工業部門綜合要素生產率并無特別大的差別。對綠色全要素生產率的研究包括前沿面與非前沿面的測度方法，前沿測試主要包括DEA 模型和隨機前沿分析等方法，當前對綠色全要素生產率和綠色全要素生產率及其增長率的研究，主要采用DEA 和SBM 模型，同時采用ML 模型，考慮非期望產出下的工業資源配置效率和技術進步效率兩個方面，當前綠色全要素生產率的非前沿方法主要基于代數箱指數核算方法，同時基于生產函數法隨著現代計量經濟學以及空間計量經濟學的發展，基于生產函數以測度綠色全要素生產率尤其是引入空間計量方法成為一種新的選擇[3-6]。

1.2 基于SBM-GML 綠色全要素生產率研究

為了實現經濟的可持續發展，改變單純依靠生產要素投入驅動當地經濟發展的模型，轉向產業轉型升級，實現所謂“結構紅利”，產業結構優化的動力來源于碳中和政策的壓力，以及工業企業為了應對碳中和戰略而主動進行綠色全要素生產率效率的提升，工業企業通過產業結構的優化并在產業結構轉型升級中進行資源有效配置并提升技術進步水平。

綠色全要素生產率（以下簡稱綠色TFP）是一個較為前沿的合成概念，基于新時代背景，在全要素生產率這一核心理念的基礎上，融入綠色、包容等要素，是對傳統全要素生產率的拓展和深化。從全球視野看，世界銀行從2012年就提出將環境因素和社會因素同時納入經濟發展之中。同時，西方學者也從綠色和綠色發展與經濟發展的三者關系進行了理論探索，認為經濟發展需要考慮社會因素和環境因素，不可偏廢。國內研究相對起步較晚，周小亮等人較早對綠色綠色增長概念進行了測量，并發現中國綠色經增長存在著區域差異，但呈現縮小和收斂的趨勢特征。

2 研究設計

2.1 樣本數據來源

本研究選取了中國31 個省份作為研究樣本，以了解這些省份在2005 年至2021 年期間的工業綠色全要素生產率。研究中考慮了三個投入變量，包括各個省份工業的資本投入、勞動力投入和能源消耗，以及兩個產出變量，即工業生產增加值和三大工業污染物排放量。

為了進行測算和分析，我們采用了Golbal-Malmquist-Luenberger（GML）指數模型[3，7]。這個模型可以幫助我們評估省域工業的綠色全要素生產率，同時考慮了各個省份的投入和產出情況。這項研究的結果對于推動我國工業的可持續發展具有重要意義。通過了解各個省份的工業綠色全要素生產率，我們可以發現改進的空間，并提供相應的建議和措施。希望這項研究能夠為相關部門和決策者提供有益的參考，促進我國的工業綠色轉型。

2.2 SBM-GML

SBM-GML 是一種用于評價生產效率和預測發展趨勢的方法。它將基于slack 的測度和基于灰色的模型相結合，用于決策單位（如企業、行業或地區）的效率分析和發展預測。SBM-GML 方法的核心思想是通過測量生產過程中的資源利用率，找出可以改進的潛在空間，并利用灰色預測模型預測未來的發展，從而提出提高生產效率的措施[3，8，9]。

目前，基于方向距離函數的ML 指數和GML 指數通常用于衡量區域或行業層面的綠色全要素生產率。由于GML 指數考慮了整個參考集，它可以有效地解決無解線性規劃和“技術回歸”的問題，并具有傳遞性和循環累積的特點。因此，在本文中，我們將使用GML 生產率指數來計算工業的綠色全要素生產率。

Global Malmquist-Luenberger（GML）生產率指數表達式為：

GML 可以進一步分解為EFFCH 和TECH 的乘積，EFFCH 包括純技術效率的變化和規模效率的變化，代表內部生產效率變化引起的產出增長的部分。技術進步是指技術進步在產出增長中所占的比重。當GML 大于1 時，表示綠色全要素生產率呈增長趨勢；當GML 小于等于1 時，綠色全要素生產率可能下降或保持不變。同樣，當EFFCH大于1 時，技術效率呈增長趨勢；當EFFCH 小于等于1時，技術效率可能逆轉或保持不變。類推，當TECH>1 時，技術進步呈增長趨勢；當TECH 小于等于1 時，技術進步可能逆轉或保持不變。

2.3 面板門檻模型

文章首先檢驗了碳排放強度在工業綠色全要素生產率中的作用，因為綠色全要素生產率在時間和空間上都存在集聚效應，即一區域現階段綠色全要素生產率程度將受以往綠色全要素生產率經驗和氣氛的影響。具體模式如下：

第二，進一步檢驗了碳排放強度對綠色全要素生產率的影響是否具有健康資本門檻的非線性影響，即在健康資本小于或者大于門檻值的情況下，碳排放強度與綠色全要素生產率是否有顯著差異。以往的研究多采用分組檢驗或者引入交叉項來檢驗，但是在連續變量分組指標（如健康資本）為樣本時，常常根據主觀判斷來選取健康資本分組值，很難探查出“健康資本”的精確門檻值。該問題可通過門檻回歸模型求解，突出優勢在于自動識別樣本數據以估算特定門檻數量和門檻值以及門檻效應的顯著性。Hansen（1999）首次提出了基于固定效應靜態面板門檻回歸建模方法。Caner 與Hansen（2004）是針對包含內生解釋變量的。

門檻效應的顯著性檢驗也可采用H0:β1=β2 的方法。若拒絕接受這一零假設，就意味著不同健康資本下的碳排放強度對于綠色全要素生產率具有顯著影響。公式只設置了健康資本唯一的門檻值，其實也有可能有λ1與λ2這兩個門檻值，雙門檻回歸模型設為公式（3）。其中，在低、中、高3 個健康資本區間，即healthit≤λ1，λ1λ2，碳排放強度對綠色全要素生產率的影響分別是β1，β2和β3

探究碳排放強度如何通過健康資本機制影響經濟的高質量發展。先使用碳排放強度對健康資本指標進行回歸，然后使用碳排放強度與健康資本對綠色全要素生產率進行同步回歸[10，11]。

2.4 變量測量

①輸入變量。碳排放強度，運用碳排放數據根據IPCC測算得出[12]，該指南是基于國家或區域邊界的碳計量方法類型。②因變量為綠色全要素生產率。由SBM-GML 測算得出。③門檻變量。健康資本方面。健康資本會反映在健康支出情況，健康資本一般用健康支出定量分析。目前，全國僅發布省級層面衛生健康支出資料，更加直接反映健康資本擠出效應，以“衛生支出/固定資產投資”作為健康資本擠出效應的度量指標。政府的健康資本以“政府的健康支出/固定資產投資”計量。

3 實證結果討論

3.1 描述性統計

在回歸模型中，門檻值被作為自變量來研究其對碳排放強度的影響。根據結果，我們可以看到門檻值對碳排放強度是顯著的，這意味著門檻值的變化會對碳排放強度產生直接的影響。具體地，在第0b 區間中，當門檻值增加1單位時，碳排放強度的增加量約為0.037，伴隨著一個1.18的標準誤。這意味著門檻值每增加1 單位，碳排放強度平均增加0.037，并且該增加與誤差范圍內的波動有關。這表明門檻值對碳排放強度的影響在不同區間上可能會發生變化。

表1 展示了中國各項經濟指標的描述性統計數據。通過觀察，可以得出以下幾點結論。

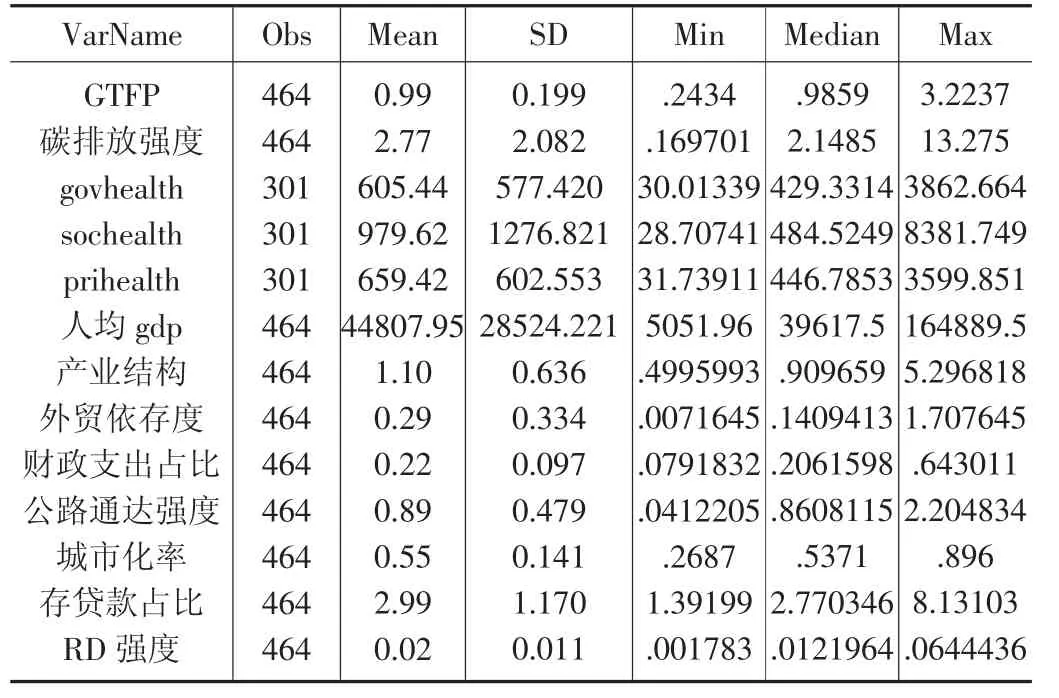
表1 描述性統計

3.2 門檻回歸分析

進行單門檻和雙門檻的判斷和分析。以下是每種門檻方案的具體判斷和分析：單門檻方案F 值為4.82，小于10.542，不滿足單門檻方案（Single）的臨界點標準。RSS 為5.5798，MSE 為0.0205，在單門檻方案下的誤差率。雙門檻方案F 值為34.66，大于21.309，滿足雙門檻方案（Double）的臨界點標準。RSS 為4.9491，MSE 為0.0182，在雙門檻方案下的誤差率。根據給出的數據，采用雙門檻方案可能是更合適的選擇，因為F 值大于雙門檻方案的臨界點標準，并且在該方案下誤差率較低，見圖1。

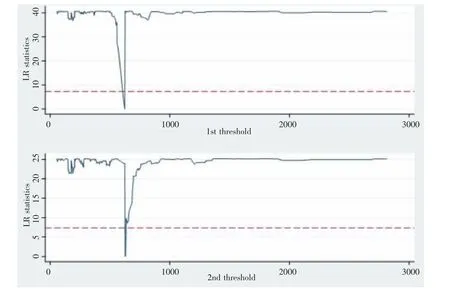
圖1 雙門檻回歸圖

4 研究結論與政策啟示

4.1 基本結論

基于SBM-GML 等方法測算省市綠色全要素生產率指數，探討了碳中和背景下健康資本對綠色全要素生產率的負向影響及其機制。本文基于“人民健康-綠色生態-經濟高質量發展”的協同演化思想，運用面板數據回歸模型進行分析，結果顯示：第一，健康資本與綠色全要素生產率具有耦合機制。第二，健康資本對綠色全要素生產率的影響具有空間差異性，即具有東部地區大于中西部地區的特征。第三，綠色全要素生產率對健康資本的反向因果效應并不明顯。

4.2 政策啟示

本文從衛生健康的視角，探索健康資本與工業綠色全要素生產率的因果機制，由于我國的衛生健康政策與經濟發展息息相關，如何協調好健康資本、生態環境與經濟高質量發展已成為較為現實的迫切課題。

第一，大力發展綠色技術，提升自主知識產權的比重。受到卡脖子技術封鎖的影響，我國需要大力提升與綠色技術綠色全要素生產率相關的產學研水平。第二，制定合理的衛生健康政策和環境規制政策。