帶電粒子在勻強電場中的動能最值問題分析

許文

帶電粒子在勻強電場中受到恒定的靜電力作用，在不同的初速度的情況下，粒子可能做直線運動，也可能做類拋體曲線運動。在一定區(qū)域內(nèi)，若粒子運動到某處時的動能最大（最小），根據(jù)動能定理可知，粒子從開始運動到此處合力做的功最大（最小）。下面通過典型實例分析帶電粒子在勻強電場中圓周上的動能最值問題，供同學們參考。

一、問題推論

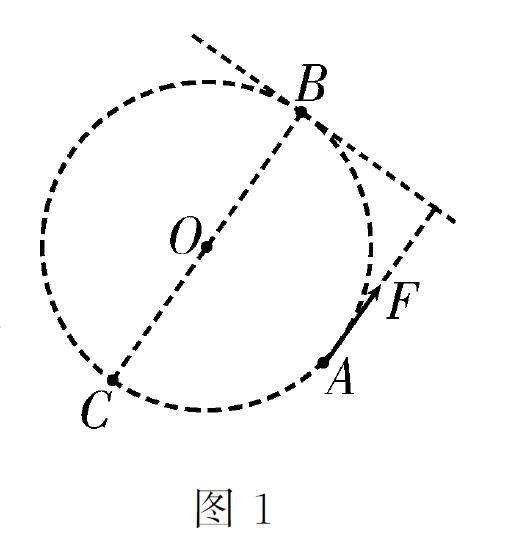
如圖1 所示，勻強電場中有一個圓周，電場方向平行于圓周平面。從圓周上某點A 在圓周平面內(nèi)沿各個方向發(fā)射初動能相同的帶電粒子，其中過圓周上B 點時粒子的動能最大。可以得出以下推論：

推論1：過B 點作圓周的切線，過A 點作此切線的垂線，則粒子受到恒定合力F 的方向與此垂線平行。

推論2：過B 點作圓的直徑與圓交于C點，則粒子經(jīng)過圓周上C 點時的動能最小。

推論3：若粒子受到的合力等于靜電力，則過B、C 點圓的切線即為勻強電場的等勢線。粒子在圓周上B 點時的電勢能最小，在圓周上C 點時的電勢能最大。

二、實例分析

根據(jù)粒子經(jīng)過圓周上動能最值點的圓的切線方向可判斷粒子受到的合力方向。若粒子受到的合力等于靜電力，則根據(jù)靜電力的方向與粒子的電性可判斷勻強電場的方向;根據(jù)電場方向可判斷圓周上各點電勢的分布情況。