核心素養背景下培養學生運算能力的措施研究

楊世成

［摘? 要］ 小學生運算能力弱的主要原因有：教師忽視運算教學的重要性、學生自身能力不足、電子產品替代人工運算等。基于培養學生核心素養的背景，研究者提出培養學生運算能力的教學策略：依托生活實際，感悟算理；借助實踐操作，理解算理；利用數學思想，突出算理；巧用錯誤資源，夯實算理。

［關鍵詞］ 運算；核心素養；教學策略

運算能力反映了學生的思維發展情況，隨著信息技術的飛速發展，電子設備成為人們生活中的常規物品，各種運算也逐漸被電子設備替代，這會對學生的運算能力發展產生一些負面影響。教師應深刻認識這一點，在數學教學中加強對學生運算能力的培養，通過各種教學手段引導學生更好地掌握算理算法，提高運算的準確率，發展數學核心素養。

一、小學生運算能力弱的原因分析

1. 教師忽視運算教學的重要性

部分教師對運算教學的重視程度不夠，教學過程中忽視對學生運算能力的培養。事實上，運算是促進學生邏輯思維發展的重要途徑，教師應對此有一個清醒的認識，重視培養學生運算能力，進而循序漸進地提升其核心素養。教師作為教學的主導者，應革新自己的理念，對運算教學產生足夠的重視，引導學生不僅關注運算結果，還要關心運算過程，感知運算帶來的樂趣。

2. 學生自身能力不足

受身心發展規律的制約，小學各個年齡階段的學生認知都有自己的特點。整體來說學生心智尚不成熟，對運算的認識比較片面，有些學生認為只要掌握基本的計算方法和獲得正確結論即可。殊不知，學生缺乏對算理過程的理解，會導致各種計算錯誤的發生。實踐證明，運算能力考驗的是學生對算理的理解程度，考查的是學生的耐心。

3. 電子產品替代人工運算

隨著時代的發展與科技的進步，電子產品成為人們生活中不可或缺的一部分，不論是在學習、工作還是生活中，電子產品確實給人們帶來了很多便利。因為隨時隨地都有電子產品的輔助，這讓部分學生覺得運算能力不那么重要，這種認識會導致他們運算意識淡薄，運算能力逐漸下降。

二、培養運算能力的措施

1. 依托生活實際，感悟算理

每一個學生都不是“空著腦袋”進入課堂的，學生在生活中都會積累一些與數學相關的經驗。教師可將學生認知中與數學相關的生活經驗挖掘出來，并將這些經驗“數學化”，讓學生探尋到思維的著陸點。教師可設計一些生活化的情境，帶領學生從自身已有的經驗出發主動發現并提出問題，同時結合自身已有的知識基礎與認知水平來解決問題，成功架起學生生活與算理算法之間的橋梁，促使學生對運算做到“知其然且知其所以然”。

案例1? “小數加、減法”的教學

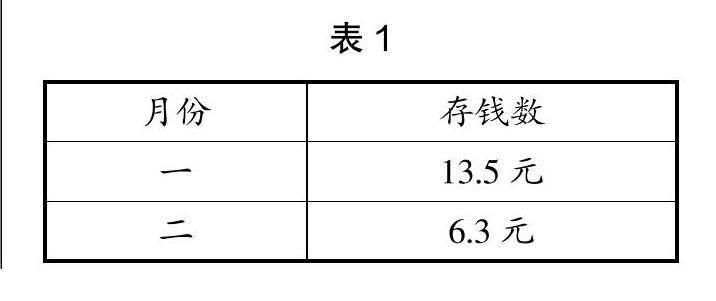
情境：小明將每個月的零花錢存到儲蓄罐中，已知一月份存了13.5元，二月份存了6.3元，請結合表1提出與數學相關的問題。

生1：小明一、二月份一共存了多少錢？

生2：小明二月份比一月份少存多少錢？

生3：一、二月份所存的錢，可列式為13.5+6.3；二月份比一月份少存的錢，可列式為13.5-6.3。

師：非常好！這兩個式子怎么計算呢？

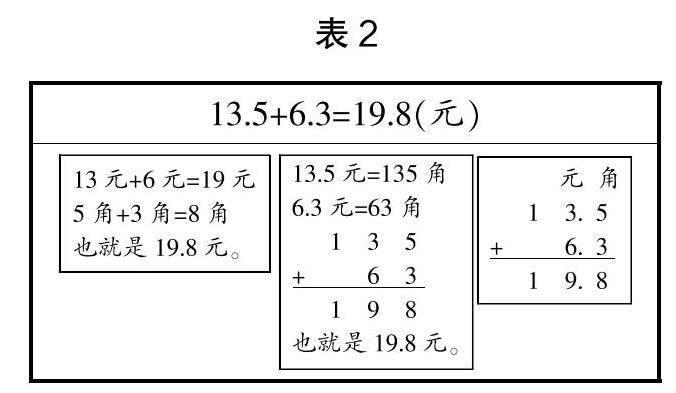
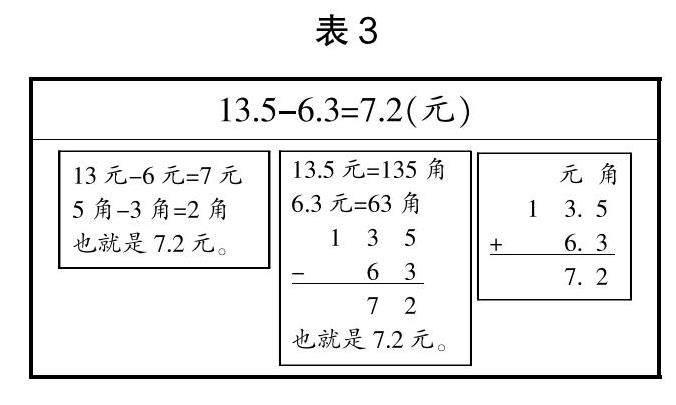
學生在討論過程中呈現出以下幾種計算方法，見表2與表3。

從學生的計算方法來看，都結合了他們的生活經驗，從元、角、分的角度去分析并計算，整個計算過程反映了學生的思維過程，自然地揭示了為什么要將小數點對齊的原理。從本例來看，分別以元、角、分為單位的情況下，只有將相同單位的數字對齊才能讓計算具有實際意義。通過計算方法的對比，同時結合整數加減法與小數加減法間的聯系，能讓學生明確小數點對齊的本質就是相同數位的對齊。此過程將生活與數學聯系起來，實現了知識的遷移。

實踐證明，為學生創設豐富的生活情境可將生活實際問題轉化成運算問題，這是賦予運算實際意義的過程，讓枯燥的計算過程變得豐富有趣；同時，學生結合自身已有的生活經驗來發現問題、提出問題、分析問題、解決問題（簡稱“四能”），能進一步理解計算的原理，發展數學運算素養。

2. 借助實踐操作，理解算理

學習應是一個生動活潑、主動且富有個性的過程，學生在課堂中聽講、思考、操作、交流等都是重要的數學學習方式。教師應為學生提供充足的時間與空間，讓學生在實踐操作中親歷操作、觀察、猜想、計算、驗證與推理等。實踐發現，實踐操作可將一些抽象難以理解的數學知識變得形象、具體，這是學生豐富表象的過程，能讓學生在實踐與觀察中獲得直接經驗與直觀體驗。

關于計算教學，教師可結合教學內容特點進行設計，引導學生在實際操作中用耳朵聽、眼睛看等，多感官參與活動過程，讓學生從更高的視角去理解問題，對知識形成豐富完整的理解，從而掌握知識本質規律，對算理與算法形成清晰、準確的認識。

案例2? “有余數的除法”的教學

為了讓學生直觀地認識余數，感知余數與除數之間存在的聯系，筆者在本節課帶領學生用小棒來搭建小正方形：搭建一個正方形需要用4根小棒，那么13，14，15…20根小棒分別能搭出幾個正方形？搭完后剩幾根？

以小組合作學習的方式開展活動，學生邊搭圖形邊填寫表格（結論見表4），然后讓學生通過對表格的觀察談一些思考與感悟。

學生自主操作、填表，發現小棒正好用完的情況下，不存在余數；小棒有剩余的情況下，存在余數；隨著小棒數量的變化，余下小棒的數量也隨之發生改變；當余數的數量達到一定程度時，又不存在余數了。兩個周期之后所有學生對“余數”產生了直觀形象的認識，并提煉出“余數必然小于除數”的結論。

學生經歷了“實踐—思考—交流—歸納”的過程，不僅自主提煉出余數與除數間的關系，還進一步訓練了數學思維，積累了活動經驗，為后續研究其他數學問題奠定了方法基礎。實踐證明，借助實物操作進行計算教學是促使學生獲得直接體驗的最佳方式，能讓學生在自主操作過程中形成的體驗與感悟，這對他們理解算理、算法具有重要意義。

此環節，在教師有效引導下，學生通過自主操作、填表、思考、總結，將實踐操作與計算有機地結合在一起，親歷知識的形成過程，能夠強化對算理、算法的掌握，提升運算能力。

3. 利用數學思想，突出算理

數形結合思想是最基本數學思想方法，正如華羅庚所言：“數形結合百般好，隔離分家萬事休。”小學數學計算中的很多算理讓學生難以理解，若借助數形結合思想和相應的描述，則能夠將學生難以理解的算理變得直觀易理解。在教學中，教師可以用點子圖、方格圖、線段圖、面積模型等促使學生形成豐富的直觀想象，從而理解算理，形成算法。

數形結合思想的應用讓抽象的算理可見、可感，讓學生在清晰的狀態下拓展思維，在觀察與思考中提煉、總結算法，促使深度學習的發生。

案例3? “兩位數乘兩位數的豎式筆算”的教學

如圖1，通過點子圖協助學生理解每一步豎式的意義，以14×12為例，其教學難點在于帶領學生理解豎式中第二步所獲得的積“14”所擺放的位置。從點子圖上來看，該式的第二步本質為14×10，因此其實際意義為140，那么它的位置應對應于十位，點子圖上將豎式每一步的算理都展現得淋漓盡致。

案例4? “分數乘分數”的教學

教師可以借助面積模型來分析計算過程，讓學生明確算理與算法。如圖2所示，分成的總份數實則為分母相乘的積，而重復陰影部分則為分子與分母相乘的積。從直觀模型中，不僅能讓學生明晰探索方法，還能促使學生從深層次理解算理，提高運算能力。

通過以上分析，不難看出圖形語言的應用可讓原本抽象的算理變得直觀易理解，使學生能更好地掌握計算的本質。通過直觀的圖展示算理，可讓學生在直觀感知中明確計算方法，將學生的思維引入深度思考。

4. 巧用錯誤資源，夯實算理

課堂是一個動態發展的過程，學生在課堂的動態發展中產生一些錯誤在所難免，教師不能將目光只鎖定在提醒或逐層設防上，應將學生制造錯誤的可能“扼殺在搖籃”中。鑒于此，在教學中教師應為學生提供廣闊的思考空間，允許錯誤的發生，將一些典型錯誤作為教學資源，帶領學生自主思錯、糾錯、辨錯，探尋錯誤形成的真實原因，避免類似錯誤再次發生。

在教師的引導下，學生追根溯源探尋錯誤的成因與根治方法，能在錯誤中實現對知識的“再認識”，從而積累學習經驗，夯實對算理的理解。

案例5? “三位數除以一位數”的教學

要求學生計算：612÷6。

如圖3，“商中間存在0”的除法計算時學生容易出現錯誤，因此教師有意識地收集了幾名學生的錯誤解法，帶領學生一起辨析這幾種算法的正確性。當學生發現問題后，教師追問：“這幾種算法錯在哪？應該怎么計算？”

學生以小組合作交流的方式與組內成員分享自己的想法，整個過程學生情緒高漲，表現出很高的積極性。

生1：第一種算法，該生漏寫了商中間的0，因為十位上的1除以6不夠，要將十位與個位上的數合起來一起除，但在寫的時候，需要將中間的0添上。

生2：后面兩種算法都將商的2寫在十位上，它所代表的意思就是2個10，顯然是錯誤的。

生3：口算就能發現這三種解法都是錯誤的，因為12×6=72，120×6=720，它們的乘積均非原式中的612，由此可確定這三個商都不正確。

生4：還可以借助分書的活動來分析這道算式，比如將612本書平均分成6份，首先考慮將600本書分成6份，每份就是100本；再將12本書分成6份，每份就是2本，因此每1份就是102本。

學生通過自主觀察、思考、分析，實現了糾錯，進一步深化了對“不夠商1時商0”算理的理解。事實證明，合理用好學生的錯誤資源，能有效發散學生思維和提升學生的“四能”。

總之，算理、算法的教學是發展學生運算能力的關鍵，也是數學教學的核心。教師應與時俱進，應用科學的方法引導學生理解算理和感悟深度學習的本質，以促進其數學思維的發展和提升其數學核心素養。