淺析轉化思想在小學數學教學中的應用

孫興華

［摘? 要］ 學生數學轉化思想的形成是一個慢過程，需要教師將其融于日常的教學活動中，引導學生通過化新為舊、化繁為簡、化數為形等途徑領悟轉化思想方法的價值，優化學生認知體系，提升學生學習品質。

［關鍵詞］ 轉化思想；學習品質；核心素養

轉化思想作為數學思想方法的重要組成部分，其在新知教學和解題教學中發揮著不可估量的作用。在學習中，學生將陌生的、復雜的問題向熟悉的、簡單的內容轉化，不僅可以降低思維的難度，而且可以提升學習信心。在面對抽象的數學問題時，學生難免會出現畏難情緒，教師可以引導學生從“形”出發，借助“形”的直觀去理解“數”，通過“數”與“形”轉化來尋找解決問題的突破口。在小學數學教學中，教師應關注學生轉化意識的培養，引導學生將“未知”轉化為“已知”，提高學生解決問題的能力。筆者結合教學實踐淺析轉化思想在小數數學教學中的應用，以期引起共鳴。

一、化新為舊，探尋知識的生長點

在新知教學中，教師可以引導學生聯系舊知識、舊方法、舊技能，通過有效的轉化尋找新知的生成點，拓展原有的認知結構。通過化新為舊培養學生創新意識，能讓學生獲得新知識、新方法、新能力。

比如，在推導平行四邊形、三角形、梯形等面積公式時，學生已經掌握了長方形的面積公式，并認識這些圖形的特征，這些知識為平行四邊形、三角形、梯形面積公式的推導提供了前提。平面圖形面積公式的推導過程蘊含著明顯的轉化思想，為了培養學生的轉化意識，教師要應用好這部分內容，以學生的已有知識為起點，引導學生通過轉化尋找新知的生長點。在教授這些內容時，教師可以引導學生將新舊圖形進行對比，在已學會的內容上尋找突破口，整理歸納新圖形的面積公式。比如在推導平行四邊形的面積公式時，教師不要直接將計算公式呈現給學生，而是直接將問題“怎樣計算平行四邊形的面積”拋給學生。對于這個問題學生是比較陌生的，這就迫使學生調用已有知識、方法尋找解決問題的突破口。學生通過對比分析發現，平行四邊形與長方形具有明顯的聯系，此時教師可以鼓勵學生通過動手操作，嘗試將平行四邊形轉化為長方形，進而推導出平行四邊形的面積公式。完成推導后，教師應預留時間讓學生反思“為什么要轉化成長方形”，讓學生體會轉化的價值，以此培養其轉化意識。

通過以上思考、交流、操作等過程，學生將不會的、陌生的知識轉化成已經學會的、熟悉的內容，順利地解決了問題。相信通過經歷以上自主探究的過程，后續在學習三角形面積和梯形面積時，學生會主動嘗試通過新舊轉化尋找新知的生長點和落腳點，為后續學習打下堅實的基礎。

二、化難為易，激發學生的興趣點

數學知識抽象且復雜，學生在學習過程中常感枯燥乏味，因此很難對數學產生好感，進而影響學生學習興趣的提升和長遠發展。在學習過程中，教師要有意識地引導學生將復雜的、難懂的問題向容易的、簡單的問題轉化，尋找解決問題的方法，培養學生學習信心和激發其學習興趣。

比如，在教學小數除法時，教師設計了這樣一個問題情境：小明和媽媽在水果店買西瓜，西瓜的價格為1.6元/千克，付款12.8元，你知道他們買的西瓜有多重嗎？情境給出后，學生很快給出算式：12.8÷1.6。小數除法是新內容，學生不知從何入手，教師應組織學生積極探尋計算方法。教師首先讓學生計算128÷16，然后引導學生思考它與12.8÷1.6之間的聯系，在教師的啟發和引導下，學生得到如下解題方法：方法1，12.8元=128角，1.6元/千克=16角/千克，128÷16=8（千克）；方法2，根據商不變的規律，將除數與被除數同時擴大原來10倍，用豎式計算。教師呈現學生的解題過程后，繼續提問：“以上解法有什么共同之處嗎？”學生很容易發現以上解法都是將小數轉化為整數計算，即轉化為已學過的方法進行求解。問題解決后，教師引導學生思考如何計算“1.28÷0.16”“128÷0.16”，引導學生進一步轉化。順利解決問題后，師生共同歸納總結除數是小數的計算方法。

這種以生活情境為切入點，運用轉化思想實現化新為舊、化難為易的轉化，既讓學生理解算理、掌握算法，又讓學生體驗轉化在小數除法中的重要應用，促進學生數學應用能力的提升。

三、化數為形，尋找問題的突破口

在面對復雜的、抽象的數學問題時，學生的思維可能會陷入困境，此時教師不要急于給出答案，可以引導學生進行數形轉化，將抽象的“數”轉化為直觀的“形”。

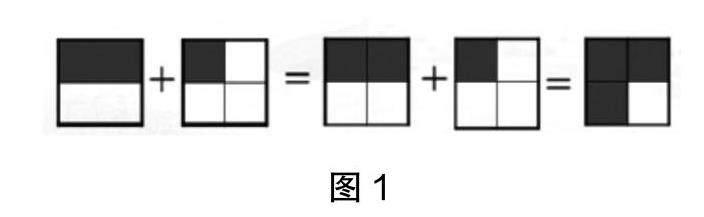
比如，在教學“異分母分數加、減法”時，如果直接告訴學生解決此類問題需要先通分再加、減，雖然學生能夠利用程序化步驟解決問題，但是學生很難理解為什么要通分。為了幫助學生明晰算理，突破思維障礙，教師可以引導學生利用圖形進行分析，從而借助圖形理解通分的意義。在探究“?+?”的計算過程中，教師可先讓學生嘗試尋找計算方法，然后出示圖1，引導學生利用“形”思考運算過程。

根據以上圖形啟發學生得到如下計算過程：?+?=2/4+?=?。將數化形，使抽象的算理變得直觀起來，有利于學生理解和接受，有利于教師提升教學效率。

四、化曲為直，提升學生空間想象能力

化曲為直是一種重要數學思想方法，在小學數學曲面圖形的面積教學時，教師可以引導學生將其轉化為無數長度很小的直線連接在一起的圖形來研究。化曲為直的轉化思想把學生的思維引向更寬廣的層次，有利于突破空間障礙，發展學生空間想象能力。

比如，在研究圓的面積時，教師引導學生運用數形結合、化新為舊、化曲為直等數學思想方法經歷圓面積公式推導的過程。在研究圓的面積前，學生已經理解并掌握長方形、平行四邊形等平面圖形面積的推導方法。教學中，教師先讓學生將圓8等分，然后拼一拼，拼出近似的平行四邊形；接下來將圓16等分，動手拼成近似平行四邊形；然后引導學生對比兩個近似平行四邊形有何不同，繼續聯想若將圓32等分和64等分，近似平行四邊形又有怎樣的變化。通過實驗、聯想等過程學生易于發現：平均分的份數越多，拼出的圖形越近似于長方形。由此通過“分一分”“拼一拼”，將平行四邊形與圓建立聯系，進而通過操作、交流推導出圓的面積公式（教師板書展示，如圖2）。

平行四邊形的面積=底×高

這種運用化曲為直的數學思想方法，將新知與舊知建立聯系，能達到化未知為已知的轉化。通過剪、擺、拼等活動，激發了學生參與課堂的積極性。在活動中，教師引導學生分析、聯想，發現平均分的份數越多越接近長方形，培養了學生的空間想象能力，發展了學生邏輯分析和邏輯推理能力。

五、化繁為簡，優化學生的認知結構

在解決問題的過程中，學生常常會遇到一些運算或數量關系比較復雜的問題，教師要引導學生想辦法化繁為簡，提高解題效率。

比如，在教學“長方形和正方形的體積”后，教師向學生提出了這樣一個問題：你能根據所學知識計算土豆的體積嗎？這是一個實際應用問題，很多學生認為土豆是不規則圖形，無法利用已學公式直接求解。教師拿出一個裝有水的長方體容器，讓學生思考借助這個容器是否能夠求土豆的體積。裝水的容器給出后，學生恍然大悟，想到運用轉化思想方法解決問題。教師預留時間讓學生動手實驗，并將實驗數據填入表1中，再讓學生利用放入前后水的體積差得到了土豆的體積。在此基礎上，教師繼續拋出問題：“還有其他方法嗎？”學生的思維被激活，進行積極思考，發現土豆的體積=長×寬×水面上升的高度。

這樣將復雜的、難以解決的問題轉化為簡單的、易于解決的問題，大大地提升了學生的解題興趣。在轉化思想的影響下，學生理解了問題的本質，在解決此類問題時自然得心應手，有助于提升解決問題的能力。

總之，在日常教學中，教師既要滲透轉化思想，又要引導學生體驗轉化思想的價值，以此提升學生的轉化意識，充分發揮轉化思想在解決問題中的價值，從而提高學生數學學習效率和提升其數學核心素養。