基于VMD模糊熵與GG聚類的直流配電網故障檢測方法

摘 要：

針對直流配電網存在的故障信號難以提取、不易對各類故障進行診斷等問題，提出一種基于變分模態分解（VMD）模糊熵與Gath-Geva（GG）聚類的故障檢測方法。首先，提取出暫態電流，采用VMD算法將故障暫態電流分解成若干個固有模態分量（IMF）。然后，分別計算分解得到的若干個IMF的模糊熵，將其作為特征向量。最后，采用GG聚類算法對故障特征的特征向量進行聚類識別。GG聚類的主要算法為將聚類樣本劃分為c類，設出隸屬度矩陣，通過設定迭代來計算聚類中心與最大似然估計距離，更新隸屬度矩陣，當隸屬度矩陣滿足條件矩陣時終止迭代，從而實現對單極故障、極間故障以及區外交流側接地故障的聚類識別。仿真結果表明，所提保護方案可靠性強、準確率高，在不同故障類型、故障位置和過渡電阻等工況下均能可靠檢測直流線路故障并準確識別故障類型，且具備一定的抗干擾能力。

關鍵詞：直流配電網；故障暫態電流；變分模態分解；模糊熵；Gath-Geva聚類；故障檢測

DOI：10.15938/j.emc.2024.02.013

中圖分類號：TM721

文獻標志碼：A

文章編號：1007-449X（2024）02-0129-13

收稿日期： 2022-01-09

基金項目：國家自然科學基金（61703144）；河南省礦山電力電子裝置與控制創新型科技團隊項目（CXTD2017085）

作者簡介：韋延方（1982—），男，博士，副教授，研究方向為電力系統及其新型輸配電的分析與控制；

王志杰（1998—），男，碩士，研究方向為電力系統故障保護；

王 鵬（1983—），男，博士，高級工程師，研究方向為智能配電網技術；

曾志輝（1978—），男，博士，副教授，研究方向為電力系統分析與控制；

王曉衛（1983—），男，博士，副教授，研究方向為配電網故障選線與定位。

通信作者：王志杰

Fault detection method for DC distribution network based on VMD fuzzy entropy and GG clustering

WEI Yanfang1，2， WANG Zhijie1， WANG Peng3， ZENG Zhihui1， WANG Xiaowei4

（1.School of Electrical Engineering and Automation， Henan Polytechnic University， Jiaozuo 454003， China; 2.Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment， Henan Polytechnic University， Jiaozuo 454003， China; 3.State Grid Henan Electric Power Company Scientific Research Institute， Zhengzhou 450052， China; 4.School of Electrical Engineering， Xi’an University of Technology， Xi’an 710000， China）

Abstract：

In response to the difficulties in extracting fault signals and diagnosing various types of faults in DC distribution networks， a fault detection method for DC distribution network based on variational mode decomposition （VMD） fuzzy entropy and Gath-Geva （GG） clustering was proposed. First， the transient current was extracted. The VMD was used to decompose the current into several intrinsic mode functions （IMF）. Then， the fuzzy entropy of several IMFs obtained by decomposition was calculated and used as the feature vector. Finally， the feature vector was input into the GG clustering analyzer for cluster recognition. In the specific algorithm of GG clustering， the cluster samples were divided into c categories. The membership matrix was set， the estimated distance was calculated between the cluster center and the maximum likelihood by setting iteration. Then the membership matrix was updated， and the iteration was terminated when the condition matrix is met. Then the cluster identification of single-pole fault， inter-pole fault and ground fault on the AC side outside the zone can be realized. The simulation results show that the proposed protection scheme has strong reliability and high accuracy， which can reliably detect DC line faults and accurately identify fault types under different fault types， fault locations and transition resistance conditions， and has a certain anti-interference ability.

Keywords：DC distribution network；the transient current; variational mode decomposition; fuzzy entropy; Gath-Geva clustering；fault detection

0 引 言

隨著分布式電力能源以及直流負荷的日益推進，利用傳統交流配電系統在新能源并網發電與功率傳輸上存在諸多瓶頸，交流配電網將面臨線路損耗大、供電走廊緊張、電壓瞬時跌落、電壓波動、電網諧波、三相不平衡現象加劇等一系列電能質量問題［1-2］。相比于傳統交流傳輸系統，直流配電系統在降低線損、節省大量分布式電源接入能耗、提高供電容量、隔離交直流故障等特點上具有明顯的優勢。隨著電力電子技術的發展，也進一步推動了直流配電網的技術革新［3-5］。基于模塊化多電平換流器（modular multilevel converter，MMC）的柔性直流配電網可獨立調節有功與無功功率，不存在換相失敗問題，其拓撲憑借輸出性能好、可向無源網絡供電且系統的控制更加靈活等優點，使其逐步應用于新能源并網等領域。但柔性直流配電網阻尼小，存在電流上升速度快、很難捕捉到故障信號等特點，導致存在無法準確識別不同故障類型的問題［6］。為避免電流過大導致設備的損壞，直流配電網需設計一種可靠識別故障線路的故障保護算法。

現有文獻對柔性直流配電網故障診斷主要研究方法有：1）行波分析。文獻［7］通過分析故障行波在線路上的傳播過程，得出區內外故障下線路端口電壓折射波幅值的正負差異特性。文獻［8］利用故障發生后的一段時間內正向行波幅值與反向幅值積分的比值進行故障識別，但是行波分析易受線路衰減、色散以及反射的影響，抗干擾能力有限。2）智能算法。文獻［9］利用小波包提取出故障頻率特征，再根據并聯卷積神經網絡對故障分類與定位做出診斷。文獻［10］通過快速傅里葉與小波變換提取出故障特征信息，再將其輸入人工神經網絡實現母線與線路故障，但是智能算法故障樣本不易提取、物理意義不清晰，需進一步工程驗證。3）邊界條件。文獻［11］利用電感電壓與直流電壓變化量來實現線路故障與母線故障的識別。文獻［12］分別計算線路一側的正、負極暫態電壓與其正常穩態電壓的標準差系數識別故障極。基于邊界條件的暫態保護，對抗干擾性的效果不佳，其方法有待更深一步研究。4）小波變換。文獻［13］利用小波時間熵的方法區別雷擊、噪聲以及故障的區分判據。文獻［14］利用小波變換提取直流電壓與母線電壓細節系數的幅值構成故障判據。基于小波變換的保護方案存在計算原理復雜、計算量大、對采樣頻率要求高等問題。因此，在選用區分故障類型的算法時，需要將抗干擾能力、提取故障樣本難易程度、耐受過渡電阻、采樣頻率要求以及計算原理復雜程度等問題考慮在內。為此，有必要進一步提出一種可靠準確、適用于區分不同故障類型的MMC型柔性直流配電網故障檢測方法。

常用的聚類算法包括譜聚類、K-means聚類、模糊C均值（fuzzy center means，FCM）聚類、Gustafaon-Kessel（GK）等，其中，FCM聚類僅適用于球形分布的數據集，GK聚類引入了自適應距離范數與協方差矩陣，可反映數據的分散程度，但其并沒有改變所產生類似于球形的聚類狀態，Gath-Geva（GG）是對FCM與GK的改進，其引入模糊最大似然估計的距離測度，適用于非規則分布的數據，可提升分類性能，反應不同形狀與方向的數據類［15］。GG聚類算法是一個迭代尋優過程，其目標函數通常以距離作為評價標準，如歐氏距離、相關系數等，依據選取的分群指標，采用該類算法對直流配電網不同的故障進行分類，可使同一類的故障信號具有較高相似度，不同故障信號將會具有明顯差異。文獻［16-17］分別對腦電睡眠分期信號以及滾動軸承故障信號進行討論，提出模糊熵（fuzzy entropy，FuzzyEn）提取信號。文獻［18］提出GG聚類算法對軸承故障信號進行分類，可準確區分軸承各類故障。目前，GG聚類算法尚未應用在直流配電網故障診斷中。

為此，本文提出一種基于變分模態分解算法（variational mode decomposition，VMD）FuzzyEn-GG聚類的故障檢測算法，該方法具有靈活的模式機制，不需要大量故障采樣樣本即可實現對各類故障的識別診斷。基于柔性直流配電網的故障特征，提取出故障暫態電流，通過VMD分解算法將暫態電流信號分解為若干個特征模態分量（intrinsic mode functions，IMF），利用FuzzyEn對IMF進行降維處理，得到表征其復雜強度的特征信息，然后將所有特征信息作為故障特征輸入到GG聚類中，即可反映不同故障下不同形狀與方向的數據類，對各類故障進行識別診斷。通過與多種算法的對比，驗證本文方法的有效性。

1 直流系統拓撲結構及故障分析

1.1 拓撲機制與運行方式

直流配電網可分為3種典型拓撲：輻射狀、雙端以及多端直流配電網等［19-20］。其中，雙端與多端相對輻射狀直流配電網供電可靠性高。本文以圖1（a）所示雙端柔性直流配電網為研究對象，采用對稱單極主接線方式。圖1（b）為基于MMC的拓撲結構，子模塊（SM）拓撲呈半橋型結構，換流站各相橋臂均由N個SM級聯構成［21-22］。圖1中：Udc為直流側電壓；idc為直流側電流；usa、usb、usc為外部交流電網變壓器二次側電壓；isa、isb、isc為外部交流電網變壓器二次側電流；ua、ub、uc為外部交流電網輸出到換流站電壓；R、L分別為交流側的等效電阻與等效電感；LS為橋臂中的等效電感；uip與uin（i=a，b，c）分別為上、下橋臂輸出電壓；iip、iin分別為流經上、下橋臂的電流；nip、nin分別為上橋臂與下橋臂分別投入SM的數量。圖1中的f1～f4為設定的故障類型，f1、f2、f3、f4分別設定為正極故障、負極故障、極間故障、交流側單相接地故障。

忽略相間環流影響，上、下橋臂中串聯的SM與交流電抗器串聯參數相同，因此上下橋臂電流為各自流向MMC交流側電流的一半。因三相電路上下橋臂對稱，可得上下橋臂電流分別為：

iip=12isi+12idc；

iin=12idc－12isi。（1）

1.2 暫態故障電流分析

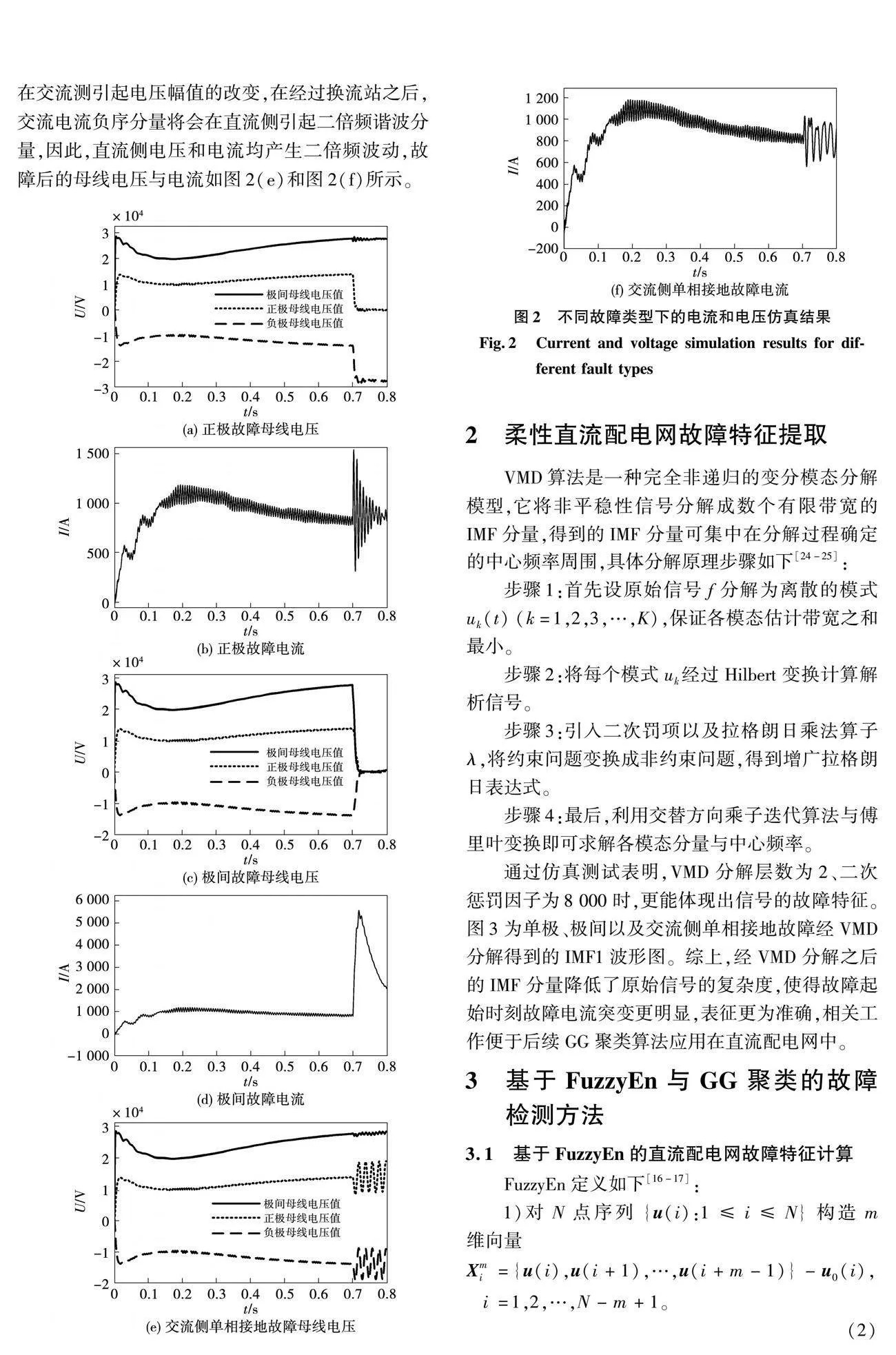
當直流配電網正極故障時（以金屬性接地故障為例），正極母線電壓迅速降為0，由于控制系統有一側是定直流電壓控制，因此，在該控制器的作用下，極間電壓Udc保持不變，從而負極母線電壓迅速增加一倍，其波形如圖2（a）所示［23］。而上橋臂存在橋臂電容，因此故障電流將會通過橋臂電容、交流側接地點以及故障電阻形成故障放電回路，導致故障電流急劇增大，但橋臂電容放電速度很快，因此故障電流急劇升高之后，亦會急劇下降，其波形如圖2（b）所示。負極故障下的電壓和電流波形與正極故障下的規律一致，限于篇幅，在此不再贅述。極間故障是直流配電網中最為嚴重的故障，相當于交流系統發生三相短路接地故障，極間故障時，正極、負極母線電壓迅速降低，極間電壓Udc也隨著正負極母線電壓下降，其波形如圖2（c）所示。而故障電流通過上下橋臂與短路點形成回路，其換流站上下橋臂的橋臂電容將迅速放電，而極間故障相對單極故障回路包含的橋臂電容較多，因此會產生很大的過電流，嚴重威脅系統的安全穩定運行，其波形如圖2（d）所示。交流側發生單相接地故障時，類似于傳統交流系統故障特征，交流電壓的負序分量首先在交流測引起電壓幅值的改變，在經過換流站之后，交流電流負序分量將會在直流側引起二倍頻諧波分量，因此，直流側電壓和電流均產生二倍頻波動，故障后的母線電壓與電流如圖2（e）和圖2（f）所示。

2 柔性直流配電網故障特征提取

VMD算法是一種完全非遞歸的變分模態分解模型，它將非平穩性信號分解成數個有限帶寬的IMF分量，得到的IMF分量可集中在分解過程確定的中心頻率周圍，具體分解原理步驟如下［24-25］：

步驟1：首先設原始信號f分解為離散的模式uk（t）（k=1，2，3，…，K），保證各模態估計帶寬之和最小。

步驟2：將每個模式uk經過Hilbert變換計算解析信號。

步驟3：引入二次罰項以及拉格朗日乘法算子λ，將約束問題變換成非約束問題，得到增廣拉格朗日表達式。

步驟4：最后，利用交替方向乘子迭代算法與傅里葉變換即可求解各模態分量與中心頻率。

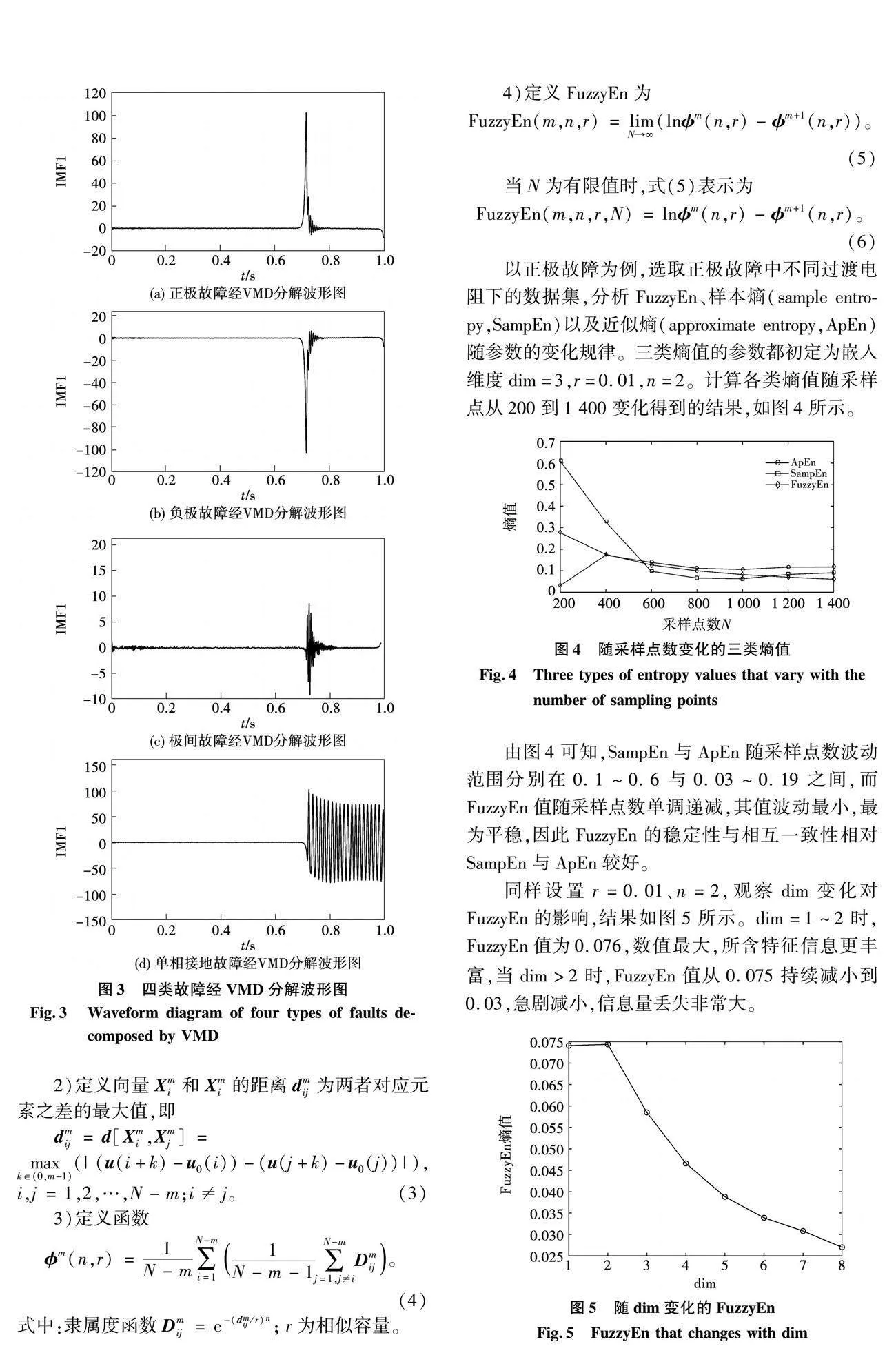
通過仿真測試表明，VMD分解層數為2、二次懲罰因子為8 000時，更能體現出信號的故障特征。圖3為單極、極間以及交流側單相接地故障經VMD分解得到的IMF1波形圖。綜上，經VMD分解之后的IMF分量降低了原始信號的復雜度，使得故障起始時刻故障電流突變更明顯，表征更為準確，相關工作便于后續GG聚類算法應用在直流配電網中。

4 仿真驗證

本文測試對象為圖1所示的MMC型柔性直流配電網，整流站和逆變站的控制方式均包括內環和外環兩部分。其中，整流站的內環為電流控制，外環為定有功功率控制，逆變站的內環為電流控制，外環為定直流電壓控制，采用鎖相器與相間環流抑制模塊，含有LC濾波環節與采樣低通濾波環節。以逆變站為例，分析直流配電網的控制系統，圖7為基于直流電壓外環的雙閉環控制器，當直流側電壓測量值升高或者降低時，可通過參考值Udref與實際測量值Udc作差，然后通過PI控制器進行誤差調節，即可使電流參考值idref穩定。由于輸出電壓基本保持恒定不變，因此對電流的控制十分重要，內環控制具有調節電流、抑制環流的作用，內環電壓控制通過接受外環控制器給定的idref用來生成控制器所需要的調制參考電壓Uaref、Ubref、Ucref ［27］。

圖7中：Ud表示直流側電壓幅值；idref、iqref為電流控制器在dq旋轉坐標系下的電流參考值；id、iq為交流側在dq旋轉坐標系下電流實際測量值。

此外，MMC型直流配電網的上下橋臂輸出電壓不平衡導致相間環流的存在，相間環流會引起橋臂電流產生畸變。為抑制相間環流，設計相間環流抑制器，如圖8所示。一般設icirdref、icirqref為0，計算相間環流值iciri，抑制系統內的二倍頻諧波，再通過PI控制器對橋臂電壓調制波進行相應調整，得到Ucirjref （j=a，b，c），從而實現對相間環流的抑制。

在MATLAB中搭建雙端五電平的MMC型直流配電網，實現dq解耦的雙閉環控制［28］。設置在0.7 s發生故障，直流系統仿真參數見表1。

為進一步有效說明VMD模糊熵與GG聚類算法的優勢，采用聚類指標：劃分系數（partition coefficient，PC）、分類熵（classification entropy，CE）、劃分熵（Xie-Beni，XB）對分類性能進行評價［29］：

PC=1n∑ci=1∑nj=1μ2ij；（12）

CE=－1n∑ci=1∑nj=1μijlnμij；（13）

XB=∑ci=1∑Nj=1（μij）m‖xj－vi‖2Nmini，j‖xj－vi‖2。（14）

4.1 故障分類仿真

測試數據類型包括正極故障、負極故障、極間故障、單相接地故障4種，每類故障樣本選取20組，正極故障、負極故障以及單相接地故障選取的接地電阻范圍是0～100 Ω，而極間故障接地電阻一般較小，選取范圍在0～10 Ω之間。樣本長度選取1 500，分別對4組故障數據進行VMD分解，取前2個分量，構成4組IMF分量數據，每組維度對1 500×2×20，通過對4組IMF分量數據求取FuzzyEn，得到4組2×20的FuzzyEn值，其FuzzyEn均值如表2所示。

由表2可知，不同故障類型的FuzzyEn不同，說明不同故障類型對應的復雜度也不同；從IMF1到IMF2的FuzzyEn均值依次減小，表明從IMF1到IMF2復雜程度也依次減小。因此，FuzzyEn表示的復雜程度可作為四類故障的特征向量，為GG聚類提供依據。此外，由表2可知，正極與負極故障中FuzzyEn大小基本一致，將其統一歸類為單極故障，聚類中心個數設為c=3，w=0.000 1，加權指數m=2。對上述3種類型FuzzyEn數據分別聚集在聚類中心V1、V2、V3附近，如圖9所示。

由圖9可知，V1～V3為聚類中心，V1有40個數據代表單極故障，V2代表極間故障，V3代表交流側單相接地故障，3種類型的數據分別聚集在聚類中心附近，聚類中心被明顯地分開，即便同一類故障所設置的過渡電阻不同，但GG聚類算法仍能將不同過渡電阻的同一類故障歸為一類，且各類故障聚集緊密，沒有出現混疊現象，類間距較大。

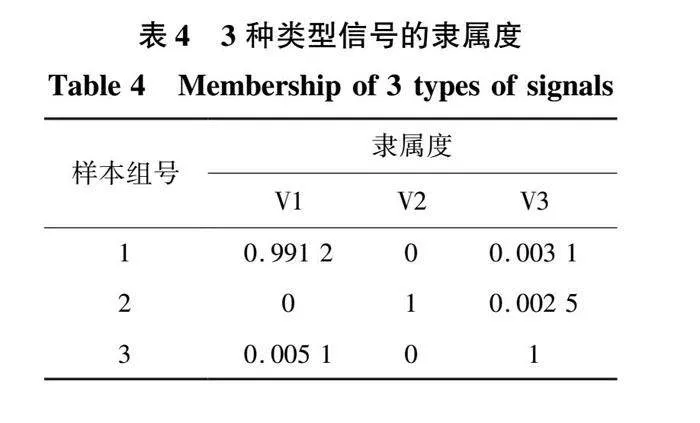
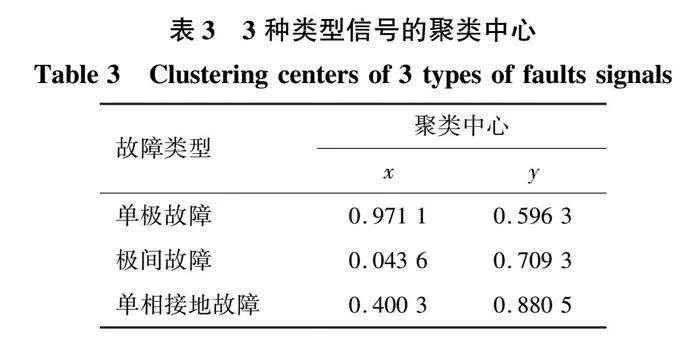
三類故障數據的聚類中心如表3所示，V1、V2、V3歸屬于三類故障信號的隸屬度如表4所示。三類故障信號的聚類中心為V1～V3。由表4可知，第一類數據集對V1的隸屬度為0.991 2，第一類數據量對V2以及V3的隸屬度分別為0、0.003 1，因此第一類樣本隸屬于V1類，即為單極故障；同理，第二類隸屬于V2，為極間故障，第三類隸屬于V3，為交流側單相接地故障。因此，該方法在MMC型柔性直流配電網的故障診斷中具有良好的效果。

4.2 柔性直流配電網故障檢測方法對比

4.2.1 FuzzyEn、SampEn與ApEn對比分析

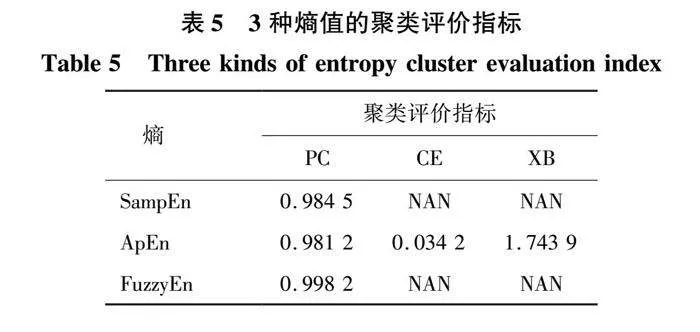
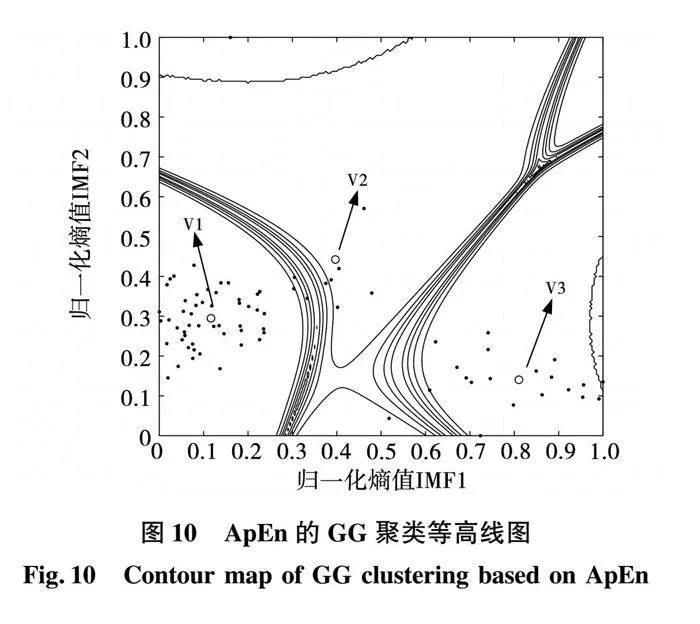
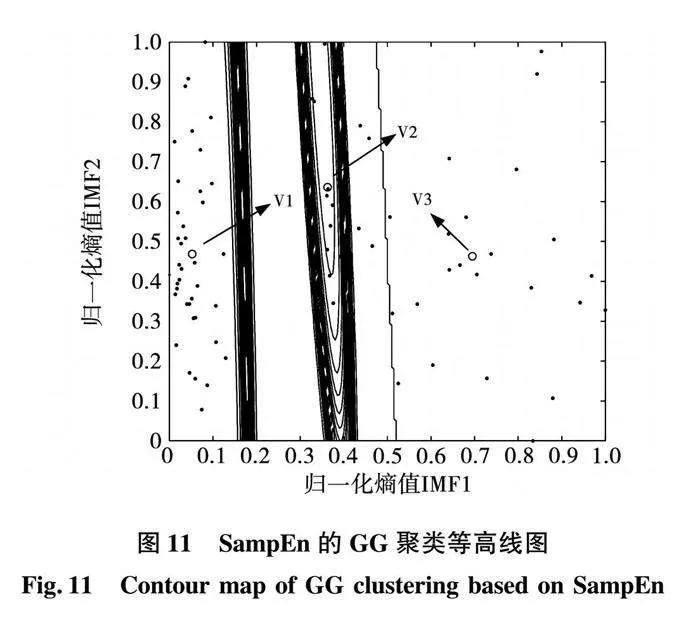
為進一步驗證FuzzyEn相對于SampEn、ApEn的優越性，對上述4組信號分別求取SampEn、ApEn，然后進行GG聚類分析，結果如圖10和圖11所示。三類熵值的聚類評價指標如表5所示。

通過對FuzzyEn-GG聚類、ApEn-GG聚類與SampEn-GG聚類的圖形對比，如圖9與圖10、圖11對比可得：

1）不同熵值對應著不同的聚類中心。

2）FuzzyEn-GG聚類結果的類內緊致性好于SampEn-GG聚類與ApEn-GG聚類，而SampEn-GG聚類與ApEn-GG聚類過于分散，不能對三類故障進行分類。

3）根據表5聚類分析指標：FuzzyEn-GG聚類PC值為0.998 2，均大于SampEn-GG聚類與ApEn-GG聚類，而FuzzyEn-GG聚類的CE與XB值最小，都為NAN。由聚類有效性可知，PC越接近1，CE、XB值越小，聚類效果越明顯，即FuzzyEn特征提取相對SampEn與ApEn更好。

4.2.2 GG聚類、GK聚類與FCM聚類對比分析

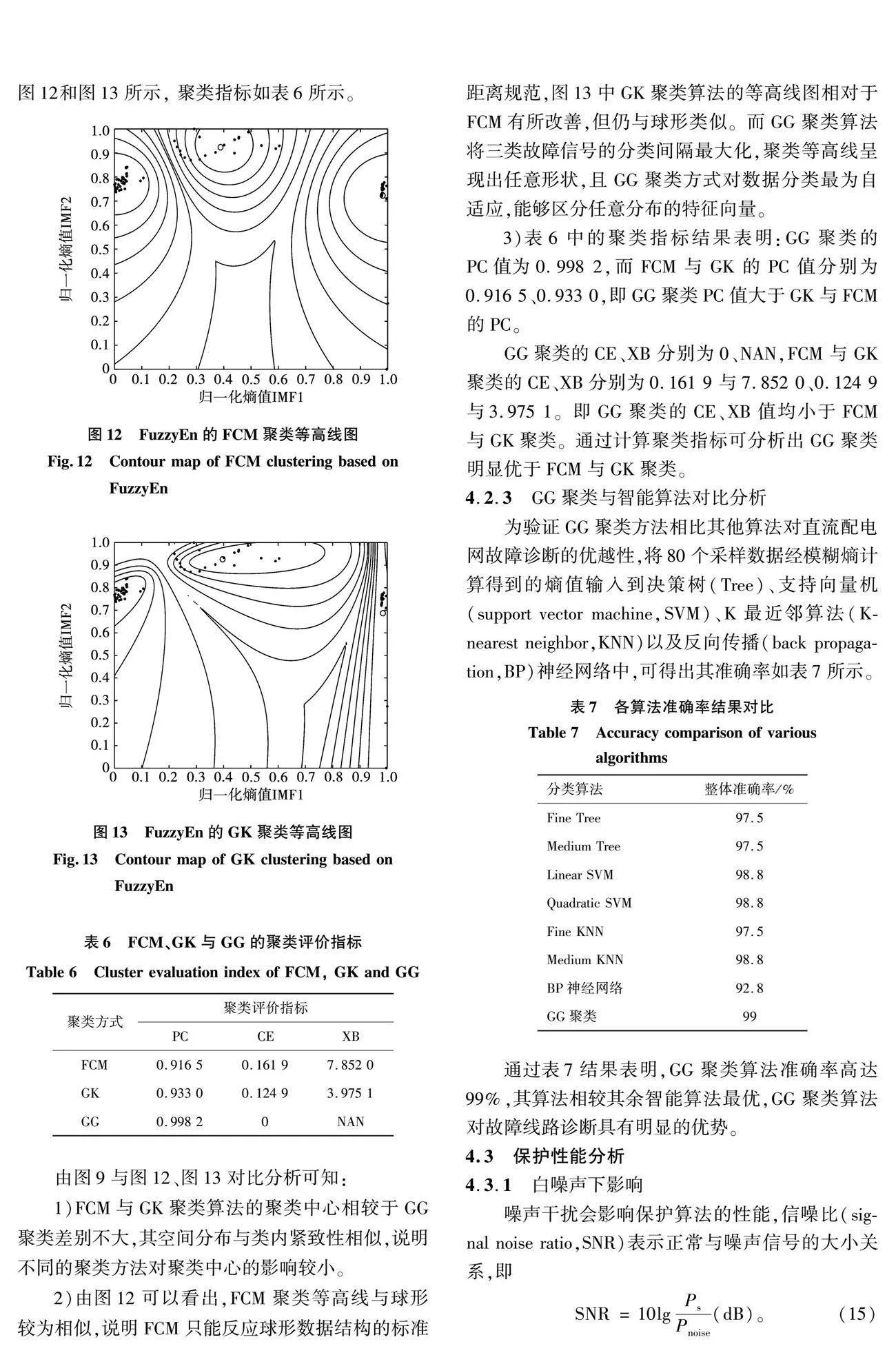
為驗證GG聚類方法相對FCM與GK的優越性，對FuzzyEn進行FCM與GK聚類分析，聚類如圖12和圖13所示， 聚類指標如表6所示。

由圖9與圖12、圖13對比分析可知：

1）FCM與GK聚類算法的聚類中心相較于GG聚類差別不大，其空間分布與類內緊致性相似，說明不同的聚類方法對聚類中心的影響較小。

2）由圖12可以看出，FCM聚類等高線與球形較為相似，說明FCM只能反應球形數據結構的標準距離規范，圖13中GK聚類算法的等高線圖相對于FCM有所改善，但仍與球形類似。而GG聚類算法將三類故障信號的分類間隔最大化，聚類等高線呈現出任意形狀，且GG聚類方式對數據分類最為自適應，能夠區分任意分布的特征向量。

3）表6中的聚類指標結果表明：GG聚類的PC值為0.998 2，而FCM與GK的PC值分別為0.916 5、0.933 0，即GG聚類PC值大于GK與FCM的PC。

GG聚類的CE、XB分別為0、NAN，FCM與GK聚類的CE、XB分別為0.161 9與7.852 0、0.124 9與3.975 1。即GG聚類的CE、XB值均小于FCM與GK聚類。通過計算聚類指標可分析出GG聚類明顯優于FCM與GK聚類。

4.2.3 GG聚類與智能算法對比分析

為驗證GG聚類方法相比其他算法對直流配電網故障診斷的優越性，將80個采樣數據經模糊熵計算得到的熵值輸入到決策樹（Tree）、支持向量機（support vector machine，SVM）、K最近鄰算法（K-nearest neighbor，KNN）以及反向傳播（back propagation，BP）神經網絡中，可得出其準確率如表7所示。

通過表7結果表明，GG聚類算法準確率高達99%，其算法相較其余智能算法最優，GG聚類算法對故障線路診斷具有明顯的優勢。

4.3 保護性能分析

4.3.1 白噪聲下影響

噪聲干擾會影響保護算法的性能，信噪比（signal noise ratio，SNR）表示正常與噪聲信號的大小關系，即

SNR=10lgPsPnoise（dB）。（15）

式中Pnoise與Ps分別代表噪聲與正常信號強度。

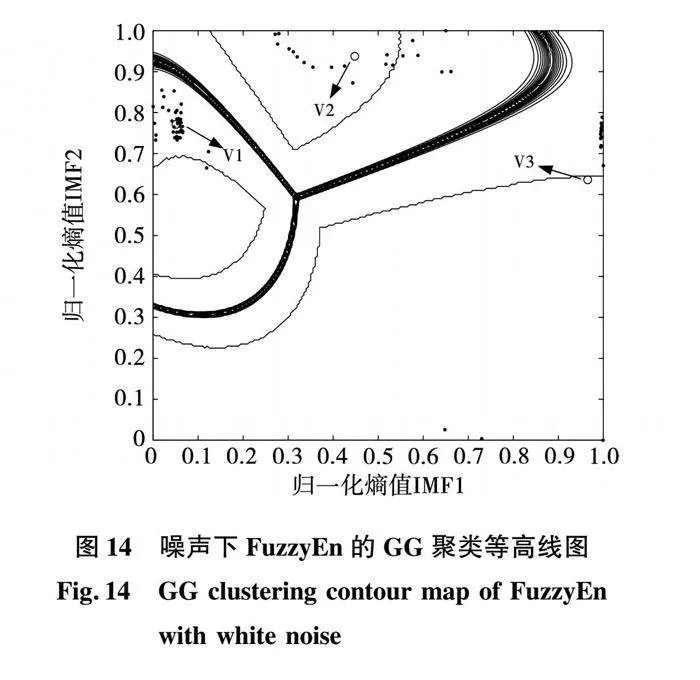
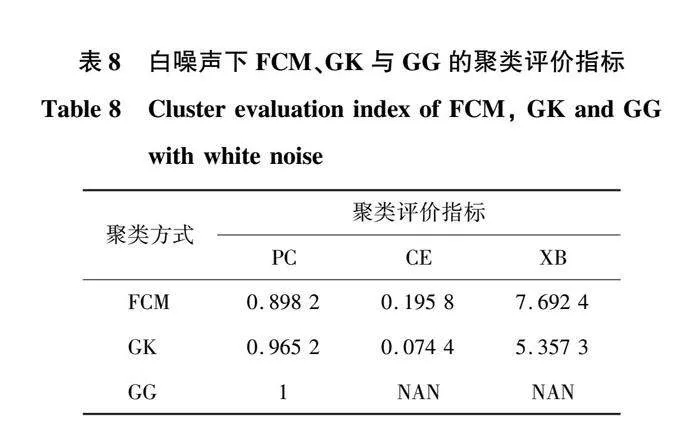
為驗證方法在強噪聲環境下的適應性，對所采集到的暫態電流信號施加信噪比為25 dB的白噪聲，GG聚類算法仿真驗證如圖14所示。不同故障類型在白噪聲下的FCM、GK、GG聚類算法的聚類指標如表8所示。

根據圖14所示，3組數據聚類中心V1、V2、V3距離較遠、類內緊致性較好，整體上可實現聚類識別且效果較好。表8表明，在噪聲下GG聚類算法依然優于FCM與GK方法。

4.3.2 不同過渡電阻下影響

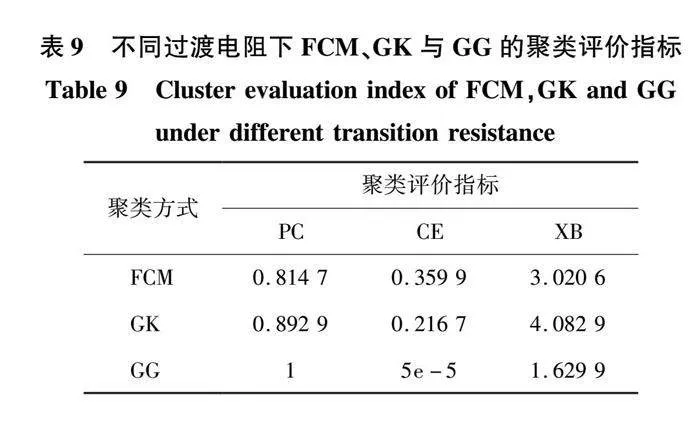
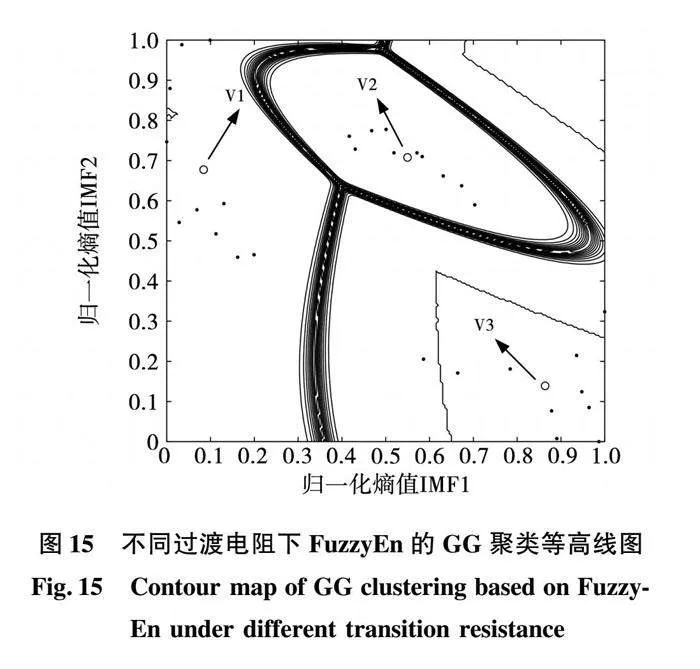
為區分3種不同過渡電阻時所提方法的實用性，以正極故障為例，在0.1～10 Ω、10～100 Ω、100 Ω以上，對3種不同過渡電阻進行樣本采集，每組10個故障信號，用VMD模糊熵與GG聚類為3種故障類型進行故障分類，如圖15所示，等高線均可將不同過渡電阻劃分到三類聚類中心附近，此方法可準確區分低阻、中阻以及高阻故障。聚類評價指標如表9所示。

由表9可知，GG聚類指標的PC=1，FCM與GK的PC值為0.814 7、0.892 9，而GG聚類的CE以及XB均小于FCM與GK的CE、XB。因此，GG聚類算法對不同過渡電阻故障識別診斷最優。

4.3.3 不同故障位置下影響

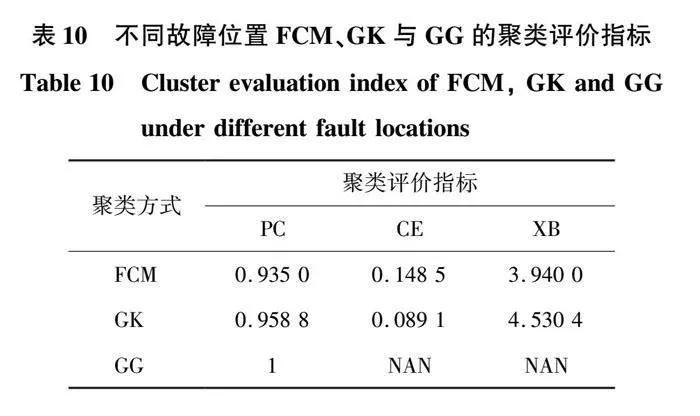
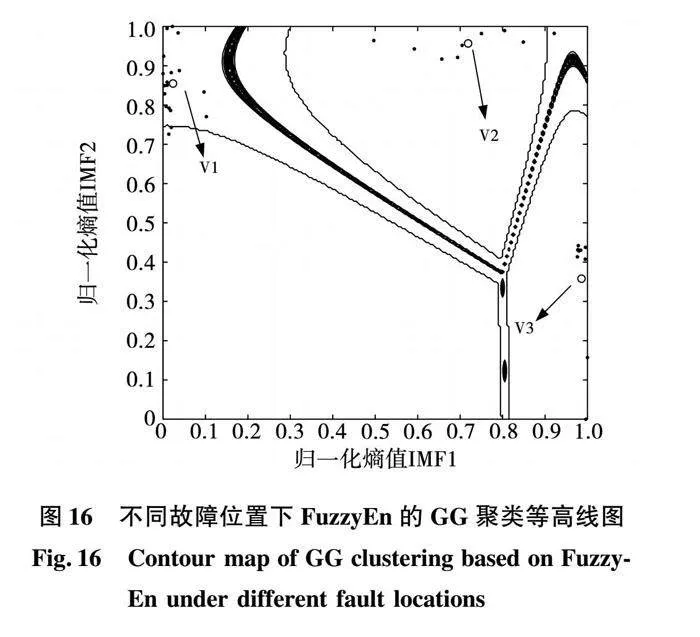
為測試不同故障位置時所提方法適用性，進一步考慮故障發生的隨機性，故障模擬在距離換流站線路4 km處分別發生單極、極間以及交流側單相接地故障（圖12、圖13在換流站10 km處發生故障），對三類故障分別采集10種不同過渡電阻的暫態電流信號，GG聚類算法仿真驗證如圖16所示。聚類評價指標如表10所示。

通過表10數據表明，GG聚類指標最優，對不同故障位置GG聚類依然優于FCM、GK聚類。

4.3.4 各工況保護性能分析

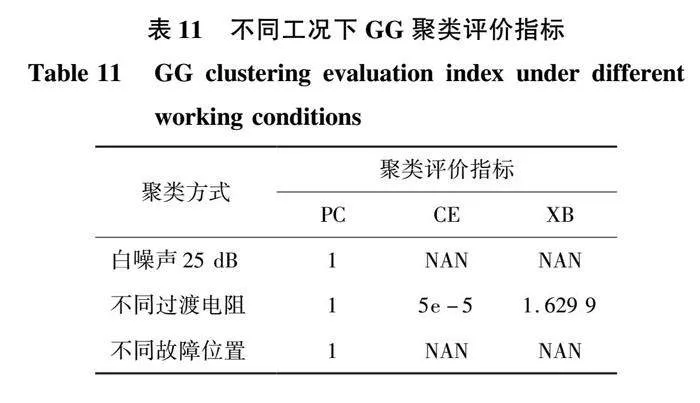
通過上述對柔性直流配電網不同工況的分析，所提VMD模糊熵與GG聚類的故障診斷方法最優，其不同工況GG聚類評價指標如表11所示。

表11數據表明，在不同白噪聲、不同故障位置以及不同極間電容的影響下，GG聚類的評價指標中的PC=1，CE與XB都為NAN，即聚類評價指標均為最優。而不同過渡電阻下的CE與XB即便不為最優值，但也可正確區分小阻接地、中阻接地以及高阻接地故障，各類故障的可隸屬度達99%。因此，所提算法適用于柔性直流配電網的故障檢測。

5 結 論

針對柔性直流配電網故障識別問題，提出一種基于暫態電流差異性的故障檢測方法。該方法利用VMD模糊熵與GG聚類算法進行柔性直流配電網的各類不同故障的分類。可得到如下結論：

1）針對故障信號較難提取問題，VMD算法分解IMF分量，可有效提取出故障電流的變化趨勢，準確反映不同故障類型的故障特征。

2）為有效獲取信號的復雜程度，采用FuzzyEn算法，降低不同故障類型的維數，使得同一故障類型下的不同故障過渡電阻歸為一類，有效解決了GG聚類算法的故障診斷精度問題。

3）為更好反應不同故障類型下的分散程度，突出不同故障類型的特征差異，采用GG聚類算法反映不同形狀的故障數據集，使同一類型下的數據更為緊湊，不同故障類型下的數據更為分散，有效解決柔性直流配電網故障樣本特征較為近似的分類問題。

4）所提方法具備較強的抗過渡電阻和耐噪聲的能力。在不同過渡電阻以及25 dB白噪聲條件干擾情況下，所提方案仍能可靠識別。

參 考 文 獻：

［1］ 靖永志，廖珍貞，龔倩文，等.VSC-HVDC送端換流器IGBT開路故障診斷方法［J］.電機與控制學報，2021，25（3）：104.

JING Yongzhi， LIAO Zhenzhen， GONG Qianwen， et al. IGBT open-circuit fault diagnosis for VSC-HVDC rectifier［J］. Electric Machines and Control，2021，25（3）：104.

［2］ 江斌開，王志新.基于VSC-MTDC的平均值建模與控制策略［J］.電機與控制學報，2018，22（3）：1.

JIANG Binkai， WANG Zhixin. Average-value modeling and control strategy of VSC-MTDC［J］. Electric Machines and Control， 2018，22（3）：1.

［3］ 劉振興，張衡，蘇茜. MMC子模塊電容電壓波動抑制［J］.電機與控制學報，2021，25（10）：139.

LIU Zhenxing， ZHANG Heng， SU qian. MMC sub-module capacitor voltage fluctuation suppression［J］. Electric Machines and Control， 2021， 25（10）： 139.

［4］ 劉宛菘，秦博宇，張若微，等.模塊化多電平換流器型多端高壓直流輸電控制參數優化方法［J］.電機與控制學報，2021，25（2）：10.

LIU Wansong， QIN Boyu， ZHANG Ruowei， et al. Optimal design method of control parameters for MMC-MTDC［J］. Electric Machines and Control，2021，25（2）：10.

［5］ 江道灼， 鄭歡. 直流配電網研究現狀與展望［J］. 電力系統自動化， 2012， 36（8）：98.

JIANG Daozhuo， ZHENG Huan. Research status and developing prospect of DC distribution network［J］. Automation of Electric Power Systems， 2012， 36（8）： 98.

［6］ 金濤，蘇見燊，張明揚.基于混合式斷路器的直流電網保護方案研究［J］.電機與控制學報，2020，24（3）：106.

JIN Tao， SU Jianshen， ZHANG Mingyang. Research on DC grid protection scheme based on hybrid circuit breaker［J］. Electric Machines and Control， 2020，24（3）：106.

［7］ 陳田田，李銀紅.基于電壓折射波幅值正負差異的柔性直流電網兩段式行波保護［J］.電力系統自動化，2022，46（3）：129.

CHEN Tiantian， LI Yinhong. Two-section traveling wave protection for flexible DC grid based on positive and negative difference of voltage refraction amplitude［J］. Automation of Electric Power Systems， 2022， 46（3）： 129.

［8］ 戴志輝， 劉自強， 楊明玉， 等. 基于暫態行波幅值積分的柔性直流電網縱聯保護［J］. 中國電機工程學報， 2020， 40（20）： 6578.

DAI Zhihui， LIU Ziqiang， YANG Mingyu， et al. Pilot protection for flexible DC grids based on amplitude integral of transient wavelet［J］. Proceedings of the CSEE， 2020， 40（20）： 6578.

［9］ 王浩， 楊東升， 周博文， 等. 基于并聯卷積神經網絡的多端直流輸電線路故障診斷［J］. 電力系統自動化， 2020， 44（12）： 84.

WANG Hao， YANG Dongsheng， ZHOU Bowen， et al. Fault diagnosis of multi-terminal HVDC transmission line based on parallel convolutional neural network［J］. Automation of Electric Power Systems， 2020， 44（12）： 84.

［10］ 楊賽昭，向往，張峻榤，等.基于人工神經網絡的架空柔性直流電網故障檢測方法［J］.中國電機工程學報，2019，39（15）：4416.

YANG Saizhao， XIANG Wang， ZHANG Junjie， et al. The artificial neural network based fault detection method for the overhead MMC based DC grid［J］. Proceedings of the CSEE，2019，39（15）：4416.

［11］ 姚良忠，吳婧，王志冰，等.柔性高壓直流環網直流側故障保護策略研究［J］.中國電機工程學報，2017，37（S1）：1.

YAO Liangzhong， WU Jing， WANG Zhibing， et al. Studies on DC fault protection strategies for MMC based HVDC grid［J］. Proceedings of the CSEE， 2017，37（S1）：1.

［12］ 余修勇，肖立業，林良真，等.基于單端量的柔性直流電網故障識別方案［J］.高電壓技術，2018，44（2）： 440.

YU Xiuyong， XIAO Liye， LIN Liangzhen， et al. Single-ended fast fault detection scheme for MMC-based HVDC［J］. High Voltage Engineering， 2018， 44（2）： 440.

［13］ 王帥，畢天姝，賈科.基于小波時間熵的MMC-HVDC架空線路單極接地故障檢測方法［J］.電網技術，2016，40（7）：2179.

WANG Shuai， BI Tianshu， JIA Ke. Wavelet entropy based single pole grounding fault detection approach for MMC-HVDC over-head lines［J］. Power System Technology， 2016，40（7）：2179.

［14］ 夏福良，秦文萍，陳武暉，等.基于正負極電流小波降噪殘差和之比的多端柔性直流系統單極接地選線方案［J］.高電壓技術，2022，48（3）：1032.

XIA Fuliang， QIN Wenping， CHEN Wuhui， et al. Single-pole grounding line selection scheme for multi-terminal flexible DC system based on the ratio of the positive and negative current wavelet noise reduction residual sum［J］. High Voltage Engineering，2022，48（3）：1032.

［15］ 趙榮珍，李霽蒲，鄧林峰. EWT多尺度排列熵與GG聚類的軸承故障辨識方法［J］.振動、測試與診斷，2019，39（2）：416.

ZHAO Rongzhen， LI Jipu， DENG Linfeng. Method integrate EWT multi-scale permutation entropy with GG clustering for bearing fault diagnosis［J］.Journal of Vibration， Measurement amp; Diagnosis， 2019， 39（2）： 416.

［16］ 劉慧，謝洪波，和衛星，等.基于模糊熵的腦電睡眠分期特征提取與分類［J］.數據采集與處理，2010，25（4）：484.

LIU Hui， XIE Hongbo， HE Weixing， et al. Characterization and classification of EEG sleep stage based on fuzzy entropy［J］. Journal of Data Acquisition amp; Processing，2010，25（4）：484.

［17］ 鄭近德，姜戰偉，代俊習，等.基于VMD的自適應復合多尺度模糊熵及其在滾動軸承故障診斷中的應用［J］.航空動力學報， 2017， 32（7）：1683.

ZHENG Jinde， JIANG Zhanwei， DAI Junxi， et al. VMD based adaptive composite multiscale fuzzy entropy and its application to fault diagnosis of rolling bearing［J］. Journal of Aerospace Power， 2017， 32（7）： 1683.

［18］ 張立國，李盼，李梅梅，等.基于ITD模糊熵和GG聚類的滾動軸承故障診斷［J］.儀器儀表學報，2014，35（11）：2624.

ZHANG Liguo， LI Pan， LI Meimei， et al. Fault diagnosis of rolling bearing based on ITD fuzzy entropy and GG clustering［J］. Chinese Journal of Scientific Instrument，2014，35（11）：2624.

［19］ 杜翼，江道灼，尹瑞，等.直流配電網拓撲結構及控制策略［J］.電力自動化設備，2015，35（1）：139.

DU Yi， JIANG Daozhuo， YIN Rui， et al. Topological structure and control strategy of DC distribution network［J］. Electric Power Automation Equipment，2015，35（1）：139.

［20］ 周嘉陽，李鳳婷，劉淵，等.基于直流電抗電壓的柔性直流配電網故障測距方法［J］.電力系統保護與控制，2018，46（19）：95.

ZHOU Jiayang， LI Fengting， LIU Yuan， et al. A fault location method for flexible DC distribution network based on DC reactor voltage［J］. Power System Protection and Control，2018，46（19）：95.

［21］ 劉天琪，周攀，王順亮，等.考慮多頻率諧波動態的模塊化多電平換流器建模及耦合特性分析［J］.電網技術，2021，45（8）：3164.

LIU Tianqi， ZHOU Pan， WANG Shunliang， et al. Modular multilevel converter modeling and coupling analysis considering multi-frequency harmonic dynamics［J］. Power System Technology，2021，45（8）：3164.

［22］ 汪濤，虞曉陽，文繼鋒，等.模塊化多電平柔性直流輸電換流器子模塊過電壓保護［J］.電力系統自動化，2020，44（21）：107.

WANG Tao， YU Xiaoyang， WEN Jifeng， et al. Sub-module overvoltage protection of modular multilevel converter for flexible DC transmission［J］. Automation of Electric Power Systems，2020，44（21）：107.

［23］ 洪翠，連淑婷，郭謀發，等.經驗小波變換在直流配電系統故障檢測中的應用［J］.電機與控制學報，2021，25（12）：65.

HONG Cui， LIAN Shuting， GUO Moufa， et al. Application of empirical wavelet transform in fault detection of DC distribution system［J］. Electric Machines and Control， 2021，25（12）：65.

［24］ 王煜塵， 竇銀科， 孟潤泉. 基于模糊C均值聚類-變分模態分解和群智能優化的多核神經網絡短期負荷預測模型［J］.高電壓技術， 2022， 48（4）： 1308.

WANG Yuchen， DOU Yinke， MENG Runquan. Multicore neural network short-term load forecasting model based on fuzzy C-mean clustering-variational modal decomposition and chaotic swarm intelligence optimization［J］. High Voltage Engineering， 2022， 48（4）： 1308.

［25］ 楊冬鋒，王鶴，劉曉軍，等.基于VMD-SVD的多端柔直電網故障測距方案［J］.電網技術，2022，46（8）：3084.

YANG Dongfeng， WANG He， LIU Xiaojun， et al. Fault location scheme for multi-terminal MMC-HVDC system based on VMD-SVD［J］. Power System Technology， 2022， 46（8）： 3084.

［26］ 王冰，胡雄，李洪儒，等.基于基本尺度熵與GG模糊聚類的軸承性能退化狀態識別［J］.振動與沖擊，2019，38（5）：190.

WANG Bing， HU Xiong， LI Hongru， et al. Rolling bearing performance degradation state recognition based on basic scale entropy and GG fuzzy clustering［J］. Journal of Vibration and Shock， 2019，38（5）： 190.

［27］ 鄭衍. 風電系統中MMC-HVDC的控制策略研究［D］.哈爾濱：哈爾濱工業大學，2019.

［28］ 付媛， 邵馨玉， 李浩. 直流配電網的暫態電壓穩定控制策略［J］.高電壓技術，2021，47（4）：1354.

FU Yuan， SHAO Xinyu， LI Hao. Transient voltage stability control strategy of DC distribution networks［J］. High Voltage Engineering， 2021，47（4）：1354.

［29］ 王志超，夏虹，朱少民，等.EWT-GG聚類的核電廠軸承故障診斷方法研究［J］.哈爾濱工程大學學報，2020，41（6）：899.

WANG Zhichao， XIA Hong， ZHU Shaomin， et al. Bearing fault diagnosis method in nuclear power plants based on EWT-GG clustering［J］. Journal of Harbin Engineering University， 2020， 41（6）： 899.

（編輯：邱赫男）