PMSM正切趨近律無位置傳感器角度補償方法研究

摘 要：

在負載轉矩突變的動態過程中，基于PI調節器的角度補償方法作用時PMSM超螺旋滑模觀測器（STSMO）轉子電角度估算誤差波動劇烈，因此依據角度估算誤差的定義，建立了轉子電角度補償算法的數學模型。根據滑模控制和趨近律理論，提出了基于正切趨近律的變步長閉環角度補償方法，選擇角度估算誤差的半角正切值作為角度調節步長，并通過前饋解耦得到的角度估算誤差正余弦信號計算該步長，實現了對無位置傳感器控制系統動態性能和抗擾動能力的改善。根據歸一化靈敏度的定義，分析調節步長隨角度估算誤差變化的靈敏度，提出了基于歸一化補償靈敏度的系統動態性能分析方法，衡量兩種補償算法作用下系統的動態性能。計算和仿真結果表明，正切趨近律補償方法具有更高的歸一化補償靈敏度，在負載轉矩突變等角度估算誤差變化劇烈的工況下能夠實現更好的補償效果，抑制估算角度誤差的波動。實驗結果表明，相比傳統的PI補償方法，正切趨近律補償方法能夠將突加額定轉矩動態過程中角度估算誤差的波動幅度降低619%，動態過程持續時間縮短23%，有效提升了系統的動態性能和抗擾動能力。

關鍵詞：永磁同步電機；無位置傳感器控制；超螺旋滑模觀測器；角度估算誤差；PI補償方法；滑模控制；正切趨近律；歸一化補償靈敏度

DOI：10.15938/j.emc.2024.01.003

中圖分類號：TM351

文獻標志碼：A

文章編號：1007-449X（2024）01-0026-09

Angle compensation method using tangent reaching law for PMSM sensorless control system

XU Qiwei，"JIANG Donghao，"WANG Yiming，"ZHANG Xuefeng，"LIU Jincheng，"CHEN Yangming

（State Key Laboratory of Power Transmission Equipment Technology， Chongqing University， Chongqing 400044， China）

Abstract：

To solve the problem that in dynamic process of sudden change of PMSM load torque， the fluctuation of supertwisting slidingmode observer （STSMO） rotor electric angle estimation error is intense even under the regulation of angle compensation method based on PI regulator， the mathematical model of PMSM rotor electric angle compensation method was established according to the definition of angle estimation error， and the variablestep closeloop angle compensation method using tangent reaching law was proposed from the perspective of slidingmode control and reaching law theory. The tangent value of half angle estimation error was chosen as angle regulating step of compensation method and was calculated by sine and cosine signal of angle estimation error obtained by feedforward decoupling algorithm， which can improve the dynamic performance as well as ability against disturbance of PMSM sensorless control system. According to the definition of normalized sensitivity， the method of system dynamic performance analysis based on normalized compensation sensitivity was proposed by analyzing the sensitivity of regulating step to the variation of angle estimation error， which can compare the dynamic performance of the system under the regulation of 2 different compensation methods. Calculation and simulation results show that the normalized compensation sensitivity of tangent method is higher than that of PI method. This means that the tangent method can achieve better compensation accuracy and suppress the fluctuation of angle estimation error when angle estimation error changes dramatically. Finally， relevant experiments have been conducted， whose results show that for experimental PMSM， tangent method can reduce the fluctuation of angle estimation error by 61.9% and shorten the transient process by 23% in dynamic process of sudden increasement of rated load torque. The dynamic performance and ability against disturbance are improved effectively.

Keywords：permanent magnet synchronous machine; sensorless control; supertwisting slidingmode observer; angle estimation error; PI compensation method; slidingmode control; tangent reaching law; normalized compensation sensitivity

0 引 言

作為一種二階滑模觀測器，超螺旋滑模觀測器（super"twisting sliding"mode observer，STSMO）結構簡單，對自身參數變化和外部擾動具有較強魯棒性，尤其是能夠顯著抑制觀測器在滑模面附近的抖振[1-2]，可以對反電動勢信號進行觀測，并通過鎖相環（phase"locked loop，PLL）對反電動勢信號包含的轉子位置信息進行提取[3-4]。因此，在中高速下表貼式永磁同步電機（surface"mounted permanent magnet synchronous machine，SPMSM）的無位置傳感器控制領域得到了廣泛的研究與應用。

理論上STSMO能夠完全抑制觀測器在滑模面附近的抖振現象，其觀測的反電動勢不需要進行低通濾波即可直接作為PLL的輸入，因此理想狀態下STSMO估算反電動勢信號中不存在相位延遲，無需對PLL估算的轉子電角度進行補償。然而，考慮到脈沖寬度調制（pulse width modulation，PWM）數據更新延遲、PLL動態跟蹤過程的時間滯后性等非理想因素的影響，實際STSMO和PLL估算轉子電角度將存在較大的角度估算誤差，尤其在負載轉矩突變的動態過程中，角度估算誤差的大幅波動可能導致電機失步，嚴重破壞系統的可靠性和穩定性。

針對SPMSM無位置傳感器控制系統中觀測器估算轉子電角度存在的角度估算誤差，國內外學者進行了大量研究，提出了多種補償方法。文獻[5]根據SPMSM參數變化造成的滑模觀測器（sliding"mode observer，SMO）角度估算誤差與逆變器母線電流之間的關系，將母線電流變化率作為誤差信號，通過PI調節器計算補償角，但需要在硬件部分增加母線電流的采樣和處理電路。文獻[6]提出使用2個同步頻率提取濾波器對SMO估算反電動勢信號中的諧波誤差進行提取和補償。然而，該方法包含多個待調整參數，導致觀測器設計的復雜程度增加。文獻[7]針對SMO趨近律使用Sigmoid函數近似代替符號函數帶來的轉子電角度估算誤差進行補償，同時采用一種前饋PLL抑制調速過程中SMO的角度估算誤差。文獻[8]提出一種基于PI調節器的SPMSM角度估算誤差全補償方法，根據SPMSM估算坐標系下的電壓方程，在電流環加入前饋解耦算法獲得角度誤差的正弦信號，之后將該信號作為誤差信號，經過PI調節器計算得到補償角。相對其他角度補償方法，該方法相對簡單，將角度估算誤差作為整體進行分析和補償，避免了針對角度估算誤差的各類產生機理進行分析，因而在SPMSM無位置傳感器控制系統中得到了廣泛的應用。

本文在仿真和實驗基礎上指出，不加角度補償算法時STSMO和PLL估算轉子電角度存在較大的角度估算誤差，揭示對STSMO和PLL估算轉子電角度進行補償的必要性；對基于PI調節器的角度補償方法進行理論和仿真分析，指出其存在負載轉矩突變的動態過程中角度估算誤差波動劇烈的問題。其次，針對這一問題，結合滑模控制和趨近律理論提出一種基于正切趨近律的變步長閉環角度補償方法，改善系統的動態性能和抗擾動能力，并提出歸一化補償靈敏度的概念，分析比較兩種補償算法作用下的系統的動態性能，同時通過仿真結果對理論分析進行驗證。最后，搭建三相SPMSM實驗臺架，對正切補償方法進行實驗驗證。

1 基于PI調節器的SPMSM角度補償

1.1 三相SPMSM"STSMO的設計

根據超螺旋滑模控制原理，三相SPMSM的二階STSMO可以設計為

式中：i^α、i^β分別是SPMSM定子α、β軸電流的觀測值；uα、uβ分別是定子α、β軸電壓；Rs、Ls分別表示定子電阻和定子電感。

超螺旋滑模控制量zα和zβ的表達式為

式中：參數k1gt;0和k2gt;0是STSMO的增益；sgn（）是符號函數；i～α、i～β表示STSMO電流觀測誤差，即

在控制量的作用下，當系統到達滑模面附近時，STSMO觀測的反電動勢可以表示為

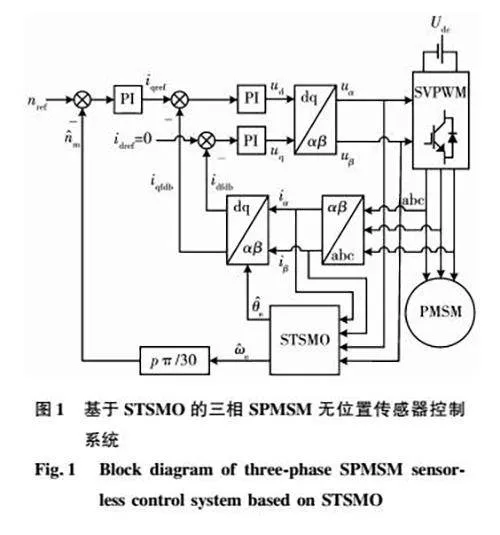
根據式（4），可以通過PLL對轉子位置進行估算。基于STSMO的SPMSM無位置傳感器控制系統的整體結構如圖1所示。

圖1中： iabc表示定子三相電流；idref、iqref分別為d^、q^軸電流環電流給定值；idfdb、iqfdb分別為d^、q^軸反饋電流；nref和n^m分別為轉速環給定值和估算機械轉速；θ^e是系統進行坐標變換采用的估算電角度。假設STSMO和PLL估算轉子電角度為θ^e_PLL，在不加入補償算法時，θ^e等于θ^e_PLL；若考慮加入角度補償算法的情況，則θ^e表示經過補償后的估算轉子電角度。

圖1所示的STSMO能夠抑制觀測器在滑模面附近的抖振，其估算反電動勢信號E^α和E^β不存在高頻抖振分量，可直接作為PLL的輸入量，不需要進行低通濾波，因而可以完全消除低通濾波器帶來的相位延遲。

1.2 基于PI調節器的閉環角度補償方法

如前所述，理想狀態下STSMO估算的轉子電角度不存在相位延遲，不需要進行補償。然而，由于采樣和計算延遲、離散化誤差等非理想因素的存在，實際STSMO在高速負載運行過程中仍然會產生較大的角度估算誤差，可能導致電機失步，破壞系統的穩定性，因此有必要對STSMO估算轉子電角度進行補償。

SPMSM無位置傳感器控制系統中，轉子電角度估算誤差通常定義為

θerr=θe－θ^e。（5）

θerr的變化范圍是［－π，π）。實際系統的采樣和計算延遲時間以及離散化誤差通常難以確定，開環角度補償算法很難精確計算角度誤差，因此必須設計一種閉環角度補償算法，實現轉子電角度的精確補償[8]。

忽略SPMSM的動態過程和轉速估算誤差，在估算轉子坐標系d^-q^下，SPMSM的電壓方程為：

根據式（6），加入前饋解耦算法后，d^-q^軸電流環PI調節器的輸出量將變為：

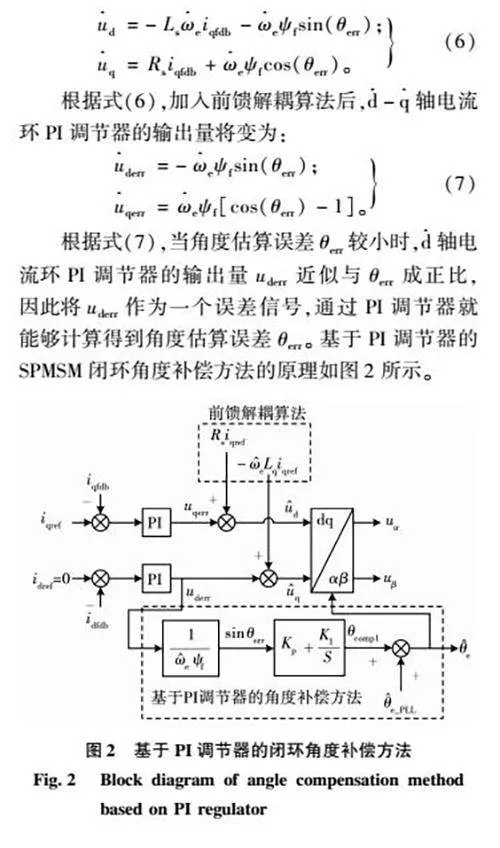
根據式（7），當角度估算誤差θerr較小時，d^軸電流環PI調節器的輸出量uderr近似與θerr成正比，因此將uderr作為一個誤差信號，通過PI調節器就能夠計算得到角度估算誤差θerr。基于PI調節器的SPMSM閉環角度補償方法的原理如圖2所示。

圖2中，參數KPgt;0和KIgt;0分別是角度補償PI調節器的比例和積分參數，θcomp1是PI補償算法輸出的補償角，系統進行坐標變換實際采用的轉子位置信號是補償后的估算轉子電角度θ^e。

2 基于正切趨近律的變步長閉環角度補償方法

2.1 基于正切趨近律的角度補償方法設計

根據文獻[8]，基于PI調節器的角度補償方法具有較高的穩態補償精確度。然而，傳統PI調節器應對時變擾動的能力較弱。此外，PI補償方法有兩個待調節參數KP和KI，算法設計和參數調節過程比較復雜。如果用滑模控制的方法控制角度估算誤差趨近于0°，不僅可以減少一個待調節參數，簡化算法的設計和參數調試過程，而且針對滑模控制的趨近律進行設計，能夠在保持滑模控制強魯棒性的同時，提高系統的動態性能。

根據上述思想，首先建立SPMSM角度補償算法的數學模型。假設在不進行補償時，轉子電角度估算誤差θerr隨時間變化的規律為

若采用最常見的等速趨近律滑模控制方法控制θerr趨近于0°，則θerr滿足的方程將變為

式中參數Kcgt;0是等速趨近律的增益。

將式（9）離散化，可以看出這種方法本質上是一種固定步長的角度補償方法。對于固定步長的調節方法，為提高穩態補償精確度，一般需要把角度調節步長設置得很小，但這會導致SPMSM無位置傳感器控制系統的動態性能變差；并且在角度估算誤差θerr接近0°時，固定的步長會導致角度估算誤差在0°兩側反復振蕩，不能準確地收斂。

為提高補償方法作用下無位置傳感器控制系統的動態性能，角度補償方法在保留滑模控制良好魯棒性的同時，還應該具有變步長的特性，即算法的調節步長能夠根據角度估算誤差的大小自動調整。當θerr的值較大時采用較大的調節步長，實現動態過程的快速跟蹤；當θerr的值較小時采用較小的調節步長，實現穩態時的精確補償。根據上述想法，本文提出一種基于正切趨近律的變步長閉環角度補償方法，其基本原理如下式：

式中參數Kgt;0是正切趨近律的增益。對式（10）進行離散化，得到正切補償方法的角度調節步長為

根據式（11），基于正切趨近律的角度補償方法是一種變步長算法，在角度估算誤差θerr的值較大時角度調節步長也較大，當θerr接近0°時調節步長也近似為0°。并且，正切函數是奇函數，其符號始終與θerr保持一致，故無需引入額外的符號函數項。另外，當θerr接近0°時，根據正切函數的泰勒展開式可知：

根據式（12），在滑模面附近，正切趨近律近似與指數趨近律等效，角度估算誤差將會以近似指數衰減的方式趨近于0°，而不是在0°附近反復振蕩。根據式（7）和式（11），角度調節步長可以設置為

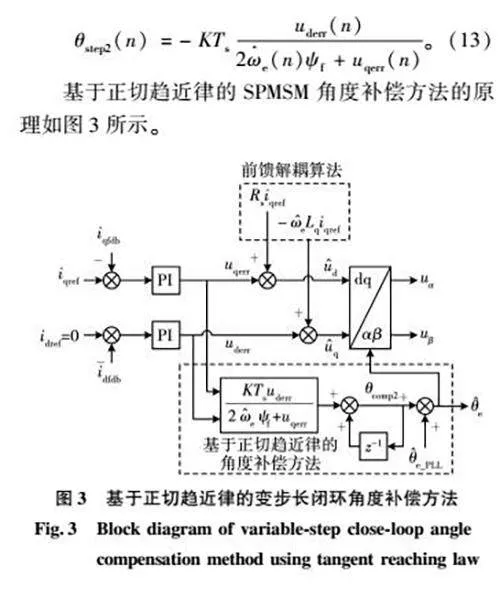
基于正切趨近律的SPMSM角度補償方法的原理如圖3所示。

圖3中，θcomp2表示正切趨近律補償方法輸出的補償角。對比圖3和圖2可知，兩種補償方法均是基于前饋解耦算法獲得式（7）所示的uderr和uqerr信號，區別在于二者分別采用PI調節器和正切趨近律計算補償角。

2.2 正切補償方法作用下系統動態性能分析

2.1節正切補償方法是針對PI補償方法作用下系統動態性能和抗擾動能力較弱的問題提出的。為分析比較兩種補償方法作用下系統的動態性能，對加入補償方法后角度估算誤差θerr滿足的方程進行分析。根據圖2可知，PI補償方法補償角的表達式為

根據式（8）和式（14），加入PI補償方法后，θerr滿足的方程可以寫成

為保持系統穩定，角度補償PI調節器的比例參數KP通常遠小于1，因此式（15）可以進一步簡化為

式（16）說明，PI補償方法可近似等效為利用指數趨近律的滑模控制方法控制θerr趨近于0°。根據式（16）可以計算出PI補償方法的調節步長為

為衡量角度補償方法作用下系統的動態性能，本文根據歸一化靈敏度的概念，提出歸一化補償靈敏度的定義如下式：

式（18）定義的歸一化補償靈敏度S反映了補償算法的調節步長隨θerr大小調整的速度。歸一化補償靈敏度越大，θstep隨θerr的調整速度也越快。對于負載突變等動態過程，θerr變化比較劇烈，S較大的補償算法的調節步長可以更快地跟隨θerr的大小進行調整，系統動態性能較好。根據式（11）、式（17）和式（18）計算得到PI補償方法和正切補償方法歸一化補償靈敏度的表達式分別如下：

由式（19）和式（20）可知，相比PI補償方法，正切補償方法的調節步長對θerr的變化更加敏感，其歸一化補償靈敏度會隨著θerr的增大而增大。當θerr增大時，正切趨近律調節步長隨θerr的調整速度也會加快，因此當施加相同擾動時，正切補償方法能夠更好地跟蹤θerr的變化，在其作用下系統的動態性能和抗擾動能力均強于PI補償方法。

3 仿真分析

3.1 不加入角度補償時STSMO仿真結果

根據圖1，搭建基于STSMO的SPMSM無位置傳感器控制系統的仿真模型，仿真所用的電機和逆變器部分參數如表1所示。

當電機在空載、1 200 r/min工況下運行時，估算轉子電角度θ^e、實際轉子電角度θe以及角度估算誤差θerr的仿真波形如圖4所示。

仿真模型中電機轉速大于300 r/min時，系統從有傳感器矢量控制切換為基于STSMO的無位置傳感器矢量控制。圖4所示的仿真結果表明，STSMO在運行過程中會產生較大的角度估算誤差，該誤差導致系統不能穩定從低速運行切換至中高轉速范圍的STSMO無位置傳感器控制系統，因此必須對STSMO和PLL估算的轉子電角度進行補償。

3.2 正切趨近律角度補償方法穩態仿真分析

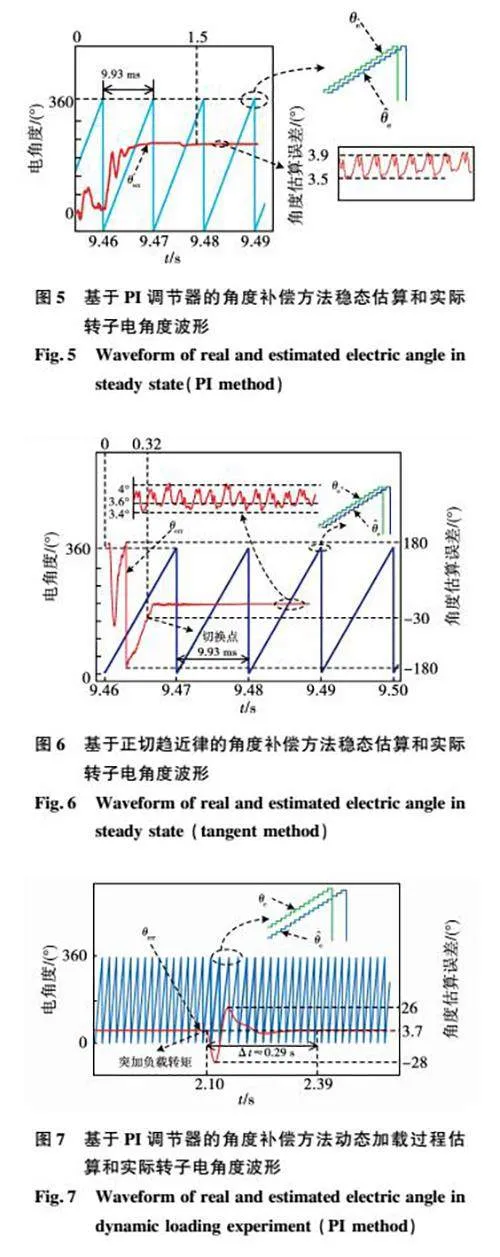
在31節的仿真模型中分別加入基于PI調節器的角度補償方法和基于正切趨近律的閉環角度補償方法，角度補償PI調節器的比例和積分參數分別設為001和10，正切趨近律的增益取為8，保持其他條件不變。運行仿真，得到兩種補償方法作用下STSMO估算轉子電角度θ^e，實際轉子電角度θe和角度估算誤差θerr的仿真波形，分別如圖5和圖6所示。

對比兩種角度補償方法作用下系統穩態運行時STSMO角度估算誤差的仿真波形，可以看出正切補償方法與PI補償方法的穩態補償精確度基本相同（穩態角度估算誤差約為36°）。穩態仿真結果說明，正切補償方法在保持與PI補償方法相同穩態精確度的同時只包含一個調節參數，其設計和調試過程相比PI補償方法更為簡單。

3.3 正切趨近律角度補償方法動態仿真分析

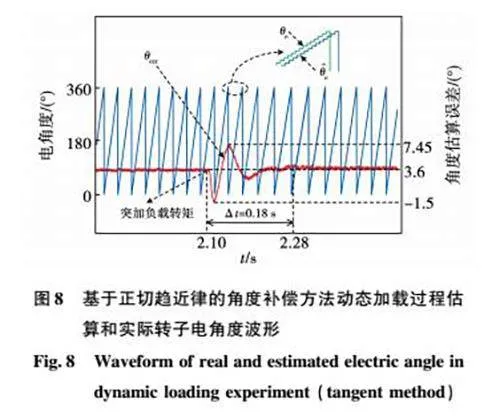
為比較兩種角度補償算法的動態補償性能和抗擾動能力，本文以32節的仿真模型為基礎，設計動態加載實驗的仿真模型，即先讓系統由空載啟動，待SPMSM的轉速達到并穩定在給定轉速后，突然將負載轉矩由0提高到額定轉矩8 N·m。PI補償方法和正切趨近律補償方法作用下，STSMO估算轉子電角度θ^e、實際轉子電角度θe和角度估算誤差θerr的動態加載仿真波形分別如圖7和圖8所示。

對比正切補償方法與PI補償方法的仿真波形可知，正切補償方法在突加額定負載的動態過程中角度估算誤差波動幅度相比PI補償方法減小了834%，動態過程持續時間縮短了379%，表明在正切補償方法作用下系統具有更強的動態補償性能和抗擾動能力，證實了22節中由歸一化補償靈敏度計算結果得出的結論。

4 實驗驗證

為了驗證本文的結論和仿真結果，搭建了如圖9所示的三相SPMSM實驗臺架進行實驗驗證。實驗電機和逆變器參數與表1相同。

4.1 不加補償時STSMO運行實驗

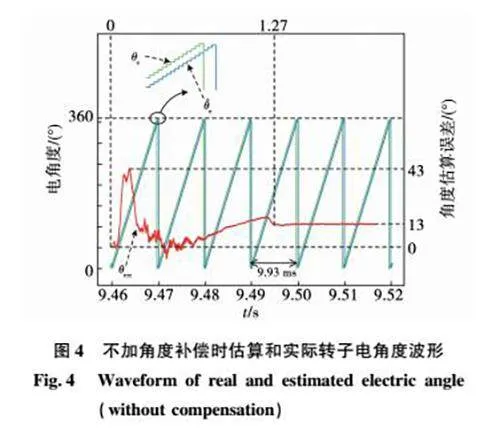
系統在零低速范圍需通過旋轉變壓器獲取轉子的位置和速度信息，當電機轉速達到550 r/min時切換到基于STSMO的無位置傳感器控制。將給定轉速和負載轉矩分別設置為500 r/min和0，可以得到不加入角度補償時STSMO估算電角度θ^e、旋變測得的轉子電角度θe和角度估算誤差θerr的實驗波形如圖10所示。

根據圖10所示的實驗波形，在不加入角度補償算法的情況下，當SPMSM的轉速達到并保持在500 r/min時，STSMO角度估算誤差約為20°，導致系統不能穩定地從有位置傳感器矢量控制系統切換到STSMO無位置傳感器控制系統。這一實驗結果與31節中的仿真結果相吻合，證明了對STSMO估算的轉子電角度進行補償的必要性。

4.2 正切趨近律角度補償方法穩態運行實驗

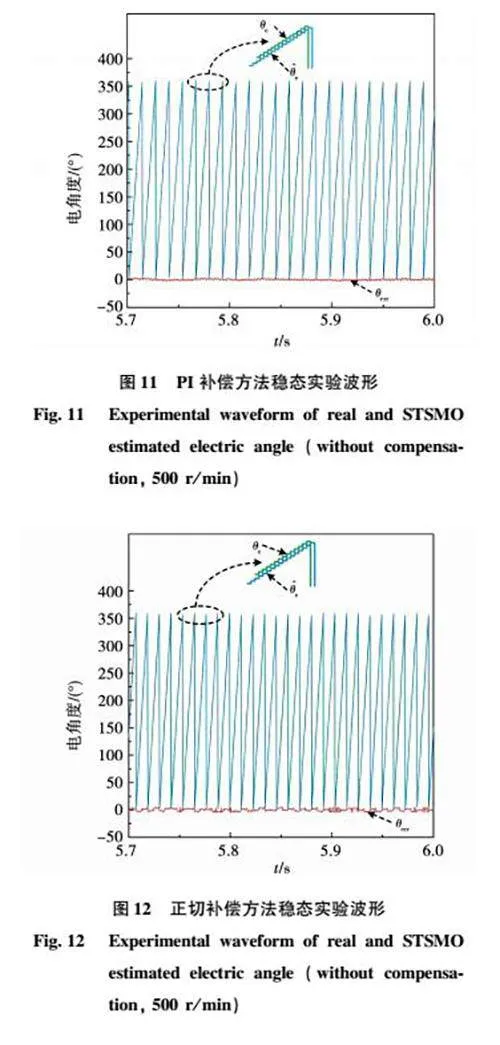
為了對比PI補償方法和本文提出的正切補償方法在SPMSM穩態運行時的補償精確度，在41節實驗的基礎上，分別加入PI補償方法和正切補償方法。將機械轉速的給定值設為1 500 r/min，負載轉矩為0，可以得到在PI補償方法和正切補償方法的作用下，SPMSM實際轉子電角度θe、STSMO估算轉子電角度θ^e和角度估算誤差θerr的穩態實驗波形，分別如圖11和圖12所示。

分別加入兩種補償方法后，系統均能夠穩定由低速范圍的有傳感器矢量控制系統切換至中高轉速范圍基于STSMO的無位置傳感器控制系統。根據圖12，當系統穩定運行在1 500 r/min時，在正切補償方法的作用下，STSMO角度估算誤差近似為05°。對比圖11和圖12實驗結果可知，正切補償方法在保持與PI補償方法相同穩態精確度的同時減少了一個待調節參數，簡化了角度補償方法的設計和調試。

4.3 正切趨近律角度補償方法動態補償實驗

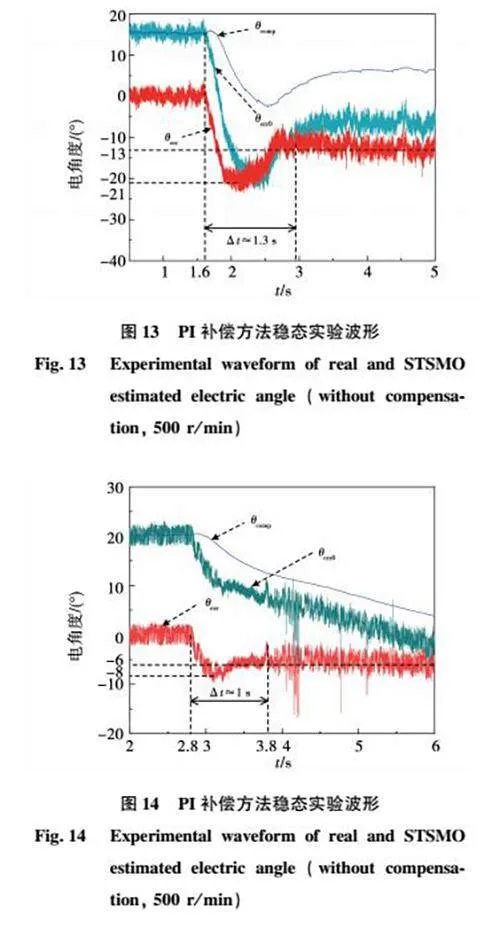
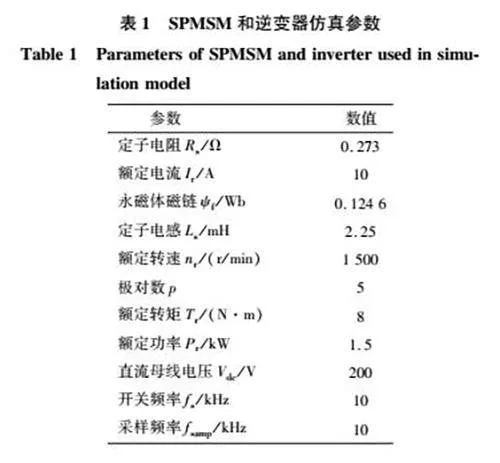
為探究正切補償方法作用下系統的動態性能，在42節穩態運行實驗的基礎上，完成突加額定負載轉矩的實驗。SPMSM加速至給定轉速1 500 r/min并達到穩態時，將負載轉矩由0突然增大至額定轉矩，可以得到在PI補償方法和正切補償方法作用下，補償角θcomp、補償前后的角度估算誤差θerr0和θerr的實驗波形，分別如圖13和圖14所示。

根據圖14，當負載轉矩突然從0增大至額定轉矩8 N·m時，正切趨近律輸出的補償角θcomp能夠跟隨θerr0變化，在其調節作用下STSMO角度估算誤差首先從穩態時的05°減小至-8°，之后緩慢增大并收斂至穩態值-6°。突加額定轉矩動態過程的持續時間Δt≈1 s，角度估算誤差的波動幅度Δθerr≈85°。對比圖13和圖14的實驗波形可知，相比PI補償方法，正切補償方法作用下角度估算誤差波動幅度減小了619%，動態過程持續時間縮短了23%，表明本文提出的正切補償方法能夠有效提升系統在突加負載過程中的動態性能，增強系統的抗擾動能力。

5 結 論

本文對基于STSMO的SPMSM無位置傳感器矢量控制系統的角度估算誤差及角度補償方法展開研究，主要成果如下；

1）針對傳統PI角度補償方法在負載轉矩突變的動態過程中波動劇烈的問題，本文結合滑模控制和趨近律理論分析了PI補償方法的性能，進而提出了基于正切趨近律的SPMSM角度補償方法，改善SPMSM"STSMO無位置傳感器控制系統的動態性能和抗擾動能力；

2）本文創新性地提出歸一化補償靈敏度的概念，衡量兩種補償算法作用下系統的動態性能，通過計算結果從理論上證明，相比PI補償方法，正切補償方法能夠明顯增強系統的動態性能和抗擾動能力；

3）仿真與實驗結果表明，本文提出基于正切趨近律的SPMSM角度補償方法具有與PI補償方法基本相同的穩態補償精確度（穩態角度估算誤差約05°）；同時具有更強的動態性能和抗擾動能力，在突加額定負載轉矩（8 N·m）的動態過程中，在基于正切趨近律的SPMSM角度補償方法作用下，STSMO角度估算誤差波動幅度（85°）與系統動態過程持續時間（1 s）相比PI補償算法均顯著降低（角度估算誤差波動幅度降低了619%，動態過程持續時間縮短了23%），證明了基于正切趨近律的角度補償方法的有效性和優越性。

參 考 文 獻：

［1］"ARIE L. Sliding order and sliding accuracy in sliding mode control [J]. International Journal of Control， 1993， 58（6）： 1247.

［2］"JORGE D， LEONID F， ARIE L. Secondorder slidingmode observer for mechanical systems [J]. IEEE Transactions on Automatic Control， 2005， 50（11）： 1785.

［3］"LIANG Donglai， LI Jian， QU Ronghai， et al. Adaptive secondorder slidingmode observer for PMSM sensorless control considering VSI nonlinearity [J]. IEEE Transactions on Power Electronics， 2018， 33（10）： 8994.

［4］"LIANG Donglai， LI Jian， QU Ronghai. Sensorless control of permanent magnet synchronous machine based on secondorder slidingmode observer with online resistance estimation [J]. IEEE Transactions on Industry Applications， 2017， 53（4）： 3672.

［5］"XIA Kun， AN Yiwen， TANG Yusong， et al. Rotor position compensation method for PMSM based on bus current precision measurement [C]// 2019 22nd International Conference on Electrical Machines and Systems （ICEMS 2019）， August 11-14， 2019， Harbin， China. 2019： 1.

［6］"SONG Xinda， FANG Jiancheng， HAN Bangcheng， et al. Adaptive compensation method for highspeed surface PMSM sensorless drives of EMFbased position estimation error [J]. IEEE Transactions on Power Electronics， 2016， 31（2）： 1438.

［7］"LIU Gang， ZHANG Haifeng， SONG Xinda. Positionestimation deviationsuppression technology of PMSM combining phase selfcompensation SMO and feedforward PLL [J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2021， 9（1）： 335.

［8］"黃科元， 高麗真， 黃守道， 等. 基于電流環誤差修正的高速永磁同步電機轉子位置校正方法[J].中國電機工程學報， 2017， 37（8）： 2391.

HUANG Keyuan， GAO Lizhen， HUANG Shoudao， et al．A correction method of rotor positions for highspeed permanent magnet synchronous motor based on the error correction of the current loop [J]. Proceedings of the CSEE， 2017， 37（8）： 2391.

（編輯：劉琳琳）

收稿日期： 2023-03-16

基金項目：重慶市自然科學基金（CSTB2022NSCQ-MSX0430）；國防科技工業核動力技術創新中心（HDLCXZX-2021-ZH-016）

作者簡介：徐奇偉（1983—），男，博士，副教授，博士生導師，研究方向為高動態性能電機驅動控制、電磁優化設計；

蔣東昊（1996—），男，碩士，研究方向為永磁同步電機驅動與控制；

王益明（1985—），男，博士，研究方向為永磁同步電機驅動與控制；

張雪鋒（1995—），男，博士，研究方向為多相電機和現代電機控制；

劉津成（1995—），男，碩士，研究方向為同步磁阻電機無位置傳感器控制；

陳楊明（1988—），男，博士，助理研究員，研究方向為電機驅動控制及其故障診斷技術、儲能管理。

通信作者：陳楊明